一種低復雜度的量子私有信息檢索協議

賀小云,裴昌幸,易運暉

(西安電子科技大學綜合業務網理論及關鍵技術國家重點實驗室,陜西西安 710071)

一種低復雜度的量子私有信息檢索協議

賀小云,裴昌幸,易運暉

(西安電子科技大學綜合業務網理論及關鍵技術國家重點實驗室,陜西西安 710071)

私有信息檢索是安全多方計算中重要的隱私保護問題,基于經典密碼學的協議在量子計算和云計算等新型技術下十分脆弱,而現有的量子私有信息檢索協議的復雜度高,在面對大型數據庫時效率低下.基于目前成熟的量子密鑰分發技術,提出了一種結合了密鑰稀釋和輔助參數兩種方法的量子私有信息檢索協議.協議中量子信道中只發送N個量子產生初始密鑰,然后對初始密鑰中連續K個比特進行按位相加去稀釋初始密鑰,產生最終密鑰去加密數據庫,并可通過靈活的選擇輔助參數θ和k來保證雙方隱私的安全性和提高檢索成功率.可行性和性能分析結果表明,協議易于實施,一次檢索成功率高,通信復雜度達到了O(N).

量子私有信息檢索;量子密鑰分發;通信復雜度;數據庫安全;用戶隱私

在大數據時代,安全多方計算是計算機科學中的熱門研究領域,是密碼學的新方向.Chor等[1]于1995年提出的私有信息檢索問題(Private Information Retrieval,PIR)就是安全多方計算的一個分支,在安全多方計算的數據庫安全查詢、匿名認證、不經意傳輸、概率可驗證明等領域有著廣闊的前景.私有信息檢索問題描述的是:服務器Bob擁有一個數據庫,其中有N個數據{d1,d2,…,dN},用戶Alice要查詢這個數據庫的某條數據di(1≤i≤N),而Bob卻不知道i的值.后來,Gertner等[2]于1998年提出對稱私有信息檢索(Symmetrically Private Information Retrieval,SPIR)協議,對服務器的數據隱私也進行保護,即Alice除了di得不到任何其他數據庫信息.

量子信息技術作為信息學與物理學相互融合產生的新興交叉學科,在運算速度、通信效率、安全性等方面均有優于或遠遠優于傳統信息技術的表現.傳統的私有信息檢索協議在量子計算和云計算等新型技術下十分脆弱,現如今出現多個用量子信息技術來解決對稱私有信息檢索問題的協議[3-6],即量子私有檢索(Quantum Private Queries,QPQ)協議.其中比較有代表性的是文獻[3,5]提出的協議,兩者分別采用量子比特編碼和相位編碼的方法,但是在應用于規模較大的數據庫時,協議中的量子計算的規模將會非常高,實現起來非常困難.

2011年,Jakobi等[7]提出了一種基于量子密鑰分發(Quantum Key Distribution,QKD)的量子私有信息檢索協議(簡稱J協議).該協議提供了很好的數據庫安全性和用戶隱私性,抗量子丟失,并可以避免常見的第三者竊聽和攻擊.由于協議基于量子密鑰分發,故可以很容易使用成熟的現有的量子密鑰分發技術來實現.但在J協議中,實現一次N比特數據庫檢索,Bob最少要通過量子通道向Alice傳送kN個量子比特.在檢索大數據庫時,例如N=108,k=13,采用較為典型的量子密鑰分發的速度1 Mbit/s[8]發送,則完成一次一個比特的檢索需要大約21 min,所付出的通信成本顯然就太高了.因此,降低通信復雜度仍是一個亟待解決的問題.

Gao等[9]在J協議基礎上提出一個更加靈活和易于實施的協議(簡稱G協議).G協議引進一個可以調節的參數θ,通過減少θ的值來降低k,從而降低通信復雜度.同樣在面對大數據庫時,如N=108,要達到一個最低的通信復雜度,即k=1,此時參數θ≈0.000 14,實現起來難度非常大.即使取一個較易實現的θ(θ= π/10),此時k=5,完成一次檢索仍然需要大約8 min,付出的通信成本依然很高,并且會大幅降低Alice的隱私性[9].

為了進一步減小通信成本,筆者基于G協議提出了一種通信復雜度更低的量子私有信息檢索協議.

1 協議流程

假設用戶Alice要從服務器Bob中檢索數據,Bob的數據庫M中的數據長度為N,Alice檢索的索引為i,協議描述如下:

步驟1 Bob準備一個量子序列,每個量子隨機地處于狀態|0〉,|1〉,|0′〉和|1′〉這4個態之一.量子態|0〉和|1〉表示0,而量子態|0′〉和|1′〉表示1.然后發給Alice,這里

其中,θ∈(0,π/2).

步驟2 Alice隨機選用基B={|0〉,|1〉}或者基B={|0′〉,|1′〉}來測量收到的量子.顯然,這次測量不會讓他推導出Bob所發量子比特的值.

步驟3 Alice隨后向Bob公布所檢測到的量子態,而拋棄掉丟失的量子.顯然Alice不能有欺騙行為,因為Alice還沒有從所發送的量子上得到任何信息,并且他不能從這次欺騙中獲益.因此,這個協議是容量子丟失的.

步驟4 對于Alice每次測量到的量子態,Bob公布0或1,這里0代表這個量子開始時處于態|0〉或者|0′〉,而1代表量子態是|1〉或者|1′〉.

步驟5 Alice根據他的測量結果和Bob公布的結果來判斷他在第1步的測量結果,他可以一定的概率p確定Bob所發的量子.例如,如果Bob公布值是0,而他在步驟2測量結果為|1〉,他只有用基B測量才可以排除|0〉,推斷出最開始所發的量子態為|0′〉,其值為1.因此,對于Bob的公布,Alice測量到正確結果的概率p=sin2θ2,不確定的概率為1-p.所有測量確定的和不確定的結果都保存下來.通過這種方式, Alice和Bob共享一個初始密鑰字符串Kr.Bob知道Kr中所有的值,而Alice只知道一部分(整個的sin2θ2).

步驟6 Bob只向Alice發送N個量子,然后停止發送.讓這N個量子作為初始密鑰Kr={k1,k2,…,kN}.Bob知道Kr中所有的值,而Alice確定其中大約Np個比特.然后對初始密鑰Kr進行稀釋,使Alice擁有確定的比特數減少為一個或幾個.雙方進行的運算為

其中,i=1,2,…,N;kN+x=kx;1≤x≤N.

經過初始密鑰Kr的稀釋,形成了一個新的長度為N的密匙K={k′1,k′2,…,k′N}.如果Alice此時沒得到一個正確的比特,則協議重新開始.不過由隨后的討論可知,這種情況發生的概率非常小.

步驟7 Alice現在準確地知道密鑰K中最少一個比特,假定為第j位元素kj,而他想檢索數據庫M中的第i位Mi.Alice為了能正確地譯碼,他向Bob公布數字s=j-i,Bob得到s后,對K移s位后得到新的密匙K′.用K′對M進行加密,可以得到加密后的數據庫M′=M⊕K′.將M′公布給Alice,Alice通過計算Mi=M′j⊕K′j,就可以得到他想查詢的數據Mi.

當θ=π/4,k=2,N=20時,Alice檢索數據庫中檢索號i=2的實現過程見表1.

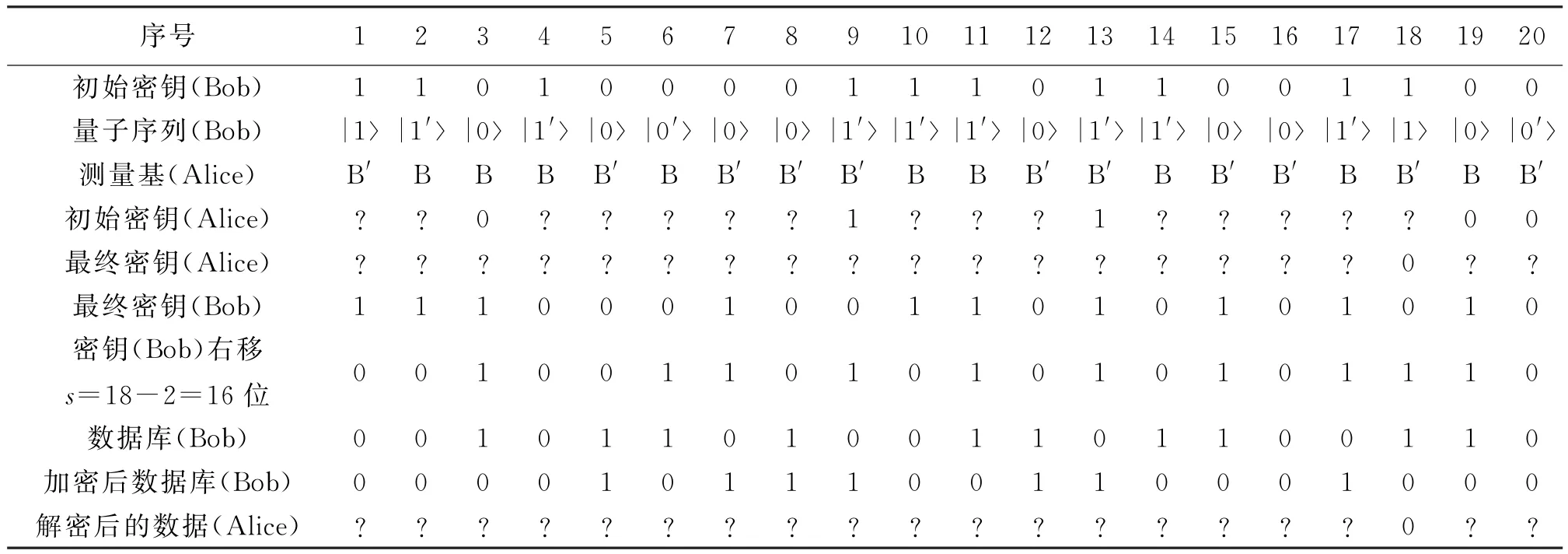
表1 一次量子私有信息檢索協議的檢索實現過程

2 可行性分析

在步驟6中,Alice在對初始密鑰進行稀釋時,必須確保初始密鑰至少存在一個連續k個確定的量子比特,這樣才能異或出一個確定值,協議才能進行下去.

將此問題進行轉換,去求首次出現連續k個確定的量子比特時的總量子比特數n′.很明顯,只有當n′＜N時,協議才是可行的.故假定有事件X,當X=1時,代表測量準確,發生的概率為p;當X=0時,代表測不準,發生的概率為1-p.計算當首次出現X連續k次為1時,總發生次數的數學期望uk.考慮如下情形:首次出現連續k-1次1,此時總次數的期望為uk-1.再測一次,結果有且只有以下兩種:

(A) 出現1,則滿足條件,所用次數的數學期望為uk-1+1.

(B) 出現0,則立即回到初始狀態,相當于又要從零開始出現k次連續1,因此總次數的數學期望為uk-1+1+uk.

A、B兩種情況的概率分別為p,1-p.因此,有

化簡后可得

顯然,此為一遞推數列.u1=1/p,可求得通項公式

其中,t=1/p,p=sin2θ/2.由式(6)知,uk是由θ和k共同來決定的.圖1給出了當θ=π/6,π/5和π/4時,由式(6)求得的uk隨k的變化曲線示意圖.可以看出,k值越大,uk越大;在k值相同時,θ小的uk要大一些.

顯然,只要合適地對θ和k取值,使uk滿足N＞uk,協議就可以進行下去.相應地,Alice在步驟6結束后,所能得到最終密鑰K中確定的比特數n約等于Nuk.將式(6)代入,可得

其中,t=1/p,p=sin2θ/2.在N和θ一定的條件下,k的取值如果過大,使N＜uk,則會有很大的概率連一個確定的比特也得不到,協議就得重新開始;而k的取值如果太小,則Alice能確定最終密鑰K中的比特數n又會太多,會造成數據庫信息的過多泄露.一個理想的k值應使Alice測量得到正確原始密鑰K中一個或者很少幾個比特.表2給出了理想情況下,當θ為π/6,π/5和π/4時,在不同的數據庫大小N下,k的取值和對應的n的關系.可以看出,在相同的數據庫下,θ越大,需要做的異或次數k就會增加.

為了保證一次檢索的成功率,碰到n只有1個多比特的時候,可適當地調整θ和k去增加n.例如表2中,當θ=π/4,N=105,k=8時,n=1.1,故此時可取θ=0.74,k=7,對應的n=2.4.通過以上對θ和k取值方法的討論,可以看出本協議在步驟6結束后,由于Alice在最終密鑰中得不到一個確定量子比特,使協議重新開始的概率很小.

圖1 不同的θ取值下,uk隨k的變化曲線

表2 在理想情況下,不同數據庫大小N下,k和n的取值

3 性能分析

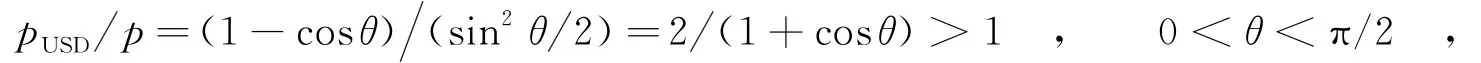
可知概率增加了.圖3就是正常測量概率和最優非歧義態區分測量后,Alice測量正確結果的概率的對比圖.當θ較小時,p和pUSD相差不多;隨著θ增大,兩者的差越來越大.因此,合適地選取θ,可以保證數據庫的隱私.

表3就是θ為π/6和π/4時,Alice正常測量和最優非歧義態區分測量確定比特數對比.可以看出,當θ較小

3.1 靈活性分析

在G協議和本協議中,對于任意的數據庫,可以通過調節θ和k來獲得一個任意想要的Alice測量得到正確原始密鑰的比特數n(n?N).但在G協議中,k是直接影響通信復雜度的.在檢索大型數據庫時,要保持一個好的通信復雜度,即要k值小,則必須采用一個很小的θ,實現起來將會十分困難.在本協議中,k已經不影響通信復雜度了,所以就不必去為了降低量子通信復雜度而采用一個非常小的θ,增加實現難度.圖2給出了當N=104,n≈3和N=106,n≈5時,由式(7)得到的k和θ的關系曲線.所以與G協議相比,本協議更加靈活,特別在檢索大型數據庫時,效率更高.

3.2隱私安全性分析

3.2.1 數據庫的安全性

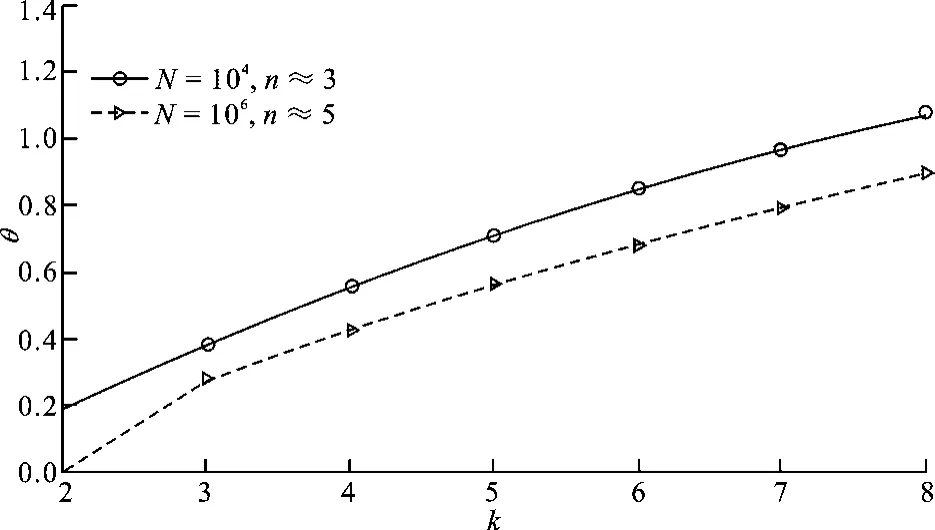
圖2 不同的數據庫N和n時,k和θ的關系曲線

如果Alice是非誠實用戶,他將收到的所有量子比特都存儲下來,就能夠在步驟4中Bob公布完后進行有效的測量.然后采用非歧義態區分(Unambiguous State Discrimination,USD)測量,由文獻[9]的分析可知,采用最優非歧義態區分測量后,Alice測量正確結果的概率pUSD=1-cosθ,由時,p和pUSD相差很小,例如當θ=π/6時,p=0.125, pUSD=0.134,使用最優非歧義態區分測量確定的最終密鑰的比特數nUSD增加不多.而θ越大,即θ=π/4時,p=0.25, pUSD=0.29,p和pUSD相差變大,使用最優非歧義態區分測量增加的確定比特數nUSD也越來越多.故從加強數據庫安全這個角度出發,應該選取較小的θ.

此外,筆者給出的協議為了提高協議的成功率,當Alice測量的確定的比特數n只有1個多比特時,調整θ和k,增加n,造成數據庫信息泄露量增加很少.這也是為了提高協議成功率所付出的代價.

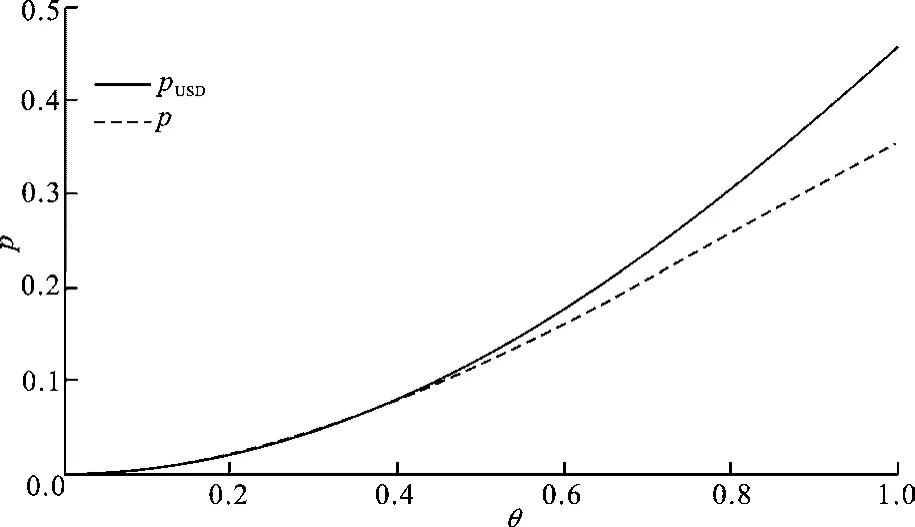
圖3 正常測量和最優非歧義態區分測量的概率比較

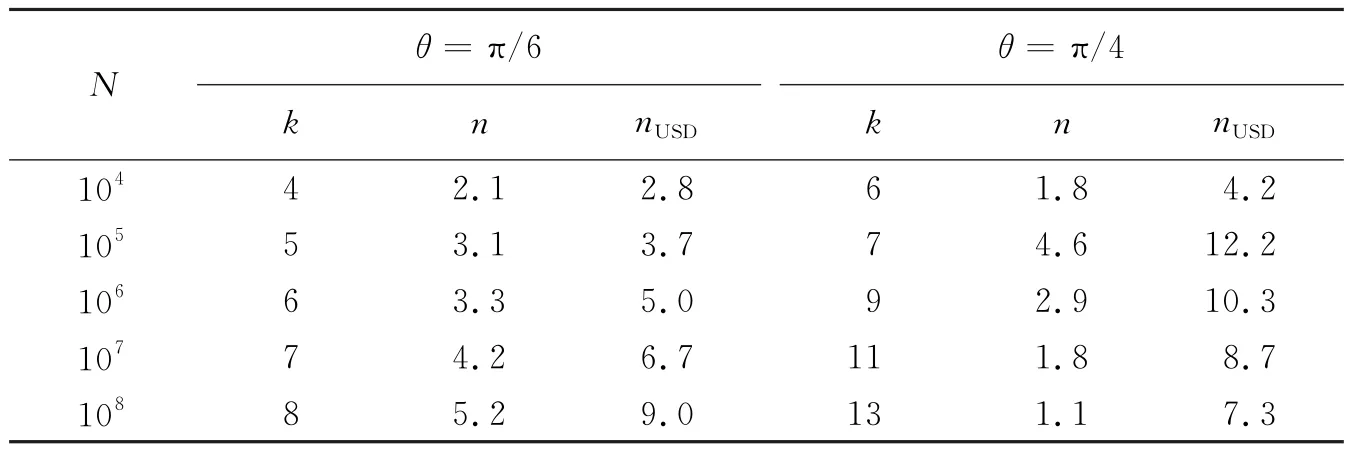
表3 正常測量和非歧義態區分測量確定比特數對比

筆者提出的協議主要是產生密鑰的方法與G協議不同,但同樣能達到數據庫安全性的要求.

3.2.2 用戶的隱私

本協議中Alice的測量結果是靠量子非正交態測不準和量子態不可克隆基本物理原理來保證的,所以Bob不可能在發送正確數據的同時還知道Alice的查詢索引,這個原因與文獻[7]中的一樣.

對于參數θ,Bob猜出Alice的檢索地址的概率pc=cos2(θ/2)[9].參數θ越小,pc越大,Bob越容易猜出Alice的檢索地址.特別地,當檢索的數據庫比較小時,如果θ也取得很小,像N=50,θ=0.6,此時k只能等于1.很明顯,Alice進行檢索時,步驟7中最終密鑰無須進行移位,所以Bob就很容易地知道Alice的檢索地址.故從加強用戶隱私性這個角度去看,應該選取大一些的θ.

當數據庫比較小時,可以將θ增大,加強Alice的隱私性,相應地泄露給Alice的數據庫比特數也增多.而數據庫很大時,這時可以適當減小θ來提高數據庫的安全性.故從數據庫的安全性和用戶的隱私兩個方面綜合考慮,通常在θ=π/4附近隨機取值.

3.3 復雜度分析

關于協議的通信復雜度.在G協議中,Bob至少需要發送k N個量子比特作為密鑰,并且k隨著數據庫N增大而增大,故綜合可知,執行一次檢索,通信復雜度大約為O(N log N)[10].而對于筆者所提協議,可以看到總共只需要發送N個量子比特,故通信復雜度達到了O(N).

再看協議所需的計算復雜度.在G協議中,在Alice方面,測量量子需要計算量為kN,在密鑰稀釋階段所需計算量為kN,在解密階段計算量為N.在Bob方面,在密鑰稀釋階段所需計算量為kN,最后數據庫加密階段計算量為N,總共需要計算量大約等于(3k+2)N.筆者提出的協議中,Alice測量量子需要計算量為N,故最后計算量大約等于(2k+3)N,約減小了(k-1)N.當檢索的數據庫規模N越大時,節約的數據處理時間越多.

4 總 結

以上提出的量子私有信息檢索協議在進行密鑰稀釋時,通過對初始密鑰中連續的k個比特進行異或,使量子信道發送的量子長度只有N,從而使通信復雜度達到最優的O(N);在檢索大小不同的數據庫時,通過合適地調節輔助參數θ和k,既提高了成功率,又可滿足安全性的要求.故本協議復雜度低,靈活性好,一次檢索成功率高,易于實現.

[1]Chor B,Goldreich O,Kushilevitz E,et al.Private Information Retrieval[C]//Proceedings of IEEE 36th Annual Symposium on Foundations of Computer Science.Los Alamitos:IEEE,1995:41-50.

[2]Gertner Y,Ishai Y,Kushilevitz E,et al.Protecting Data Privacy In Private Information Retrieval Schemes[C]// Proceedings of 13th Annual ACM Sytnposium on Theory of Computing.New York:ACM,1998:151-160.

[3]Giovannetti V,Lloyd S,Maccone L.Quantum Private Queries[J].Physical Review Letter,2008,100(23):230502.

[4]Giovannetti V,Lloyd S,Maccone L.Quantum Private Queries:Security Analysis[J].IEEE Transactions on Information Theory,2010,56(7):3465-3477.

[5]Olejnik L.Secure Quantum Private Information Retrieval Using Phase-encoded Queries[J].Physical Review A,2011, 84(2):022313-022316.

[6]De Martini F,Giovannetti V,Lloyd S,et al.Experimental Quantum Private Queries with Linear Optics[J].Physical Review A,2009,80(1):010302-010305.

[7]Jakobi M,Simon C,Gisin N,et al.Practical Private Database Queries Based on a Quantum Key Distribution Protocol [J].Physical Review A,2011,83(2):2301-2306.

[8]Dixon A R,Yuan Z L,Dynes J F,et al.Continuous Operation of High Bit Rate Quantum Key Distribution[J].Applied Physics Letters,2010,96(16):1102-1104.

[9]Gao F,Liu B,Wen Q Y.Flexible Quantum Private Queries Based on Quantum Key Distribution[J].Optics Express, 2012,20(16):17411-17420.

[10]Brassard G.Quantum Communication Complexity[J].Foundations of Physics,2003,33(11):1593-1616.

(編輯:郭 華)

Low complexity quantum private queries protocol

HE Xiaoyun,PEI Changxing,YI Yunhui
(State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China)

Private information retrieval(PIR)is an important privacy protection issue of secure multi-party computation,but the PIR protocols based on classical cryptography are vulnerable because of new technologies,such as quantum computing and cloud computing.The quantum private queries(QPQ) protocols available,however,has a high complexity and is inefficient in the face of large database.This paper,based on the QKD technology which is mature now,proposes a novel QPQ protocol utilizing the key dilution and auxiliary parameter.Only N quits are required to be sent in the quantum channel to generate the raw key,then the straight k bits in the raw key are added bitwise to dilute the raw key,and a final key is consequently obtained to encrypt the database.By flexible adjusting of auxiliary parametersθand k,privacy is secured and the query success ratio is improved.Feasibility and performance analyses indicate that the protocol has a high success ratio in first-trial query and is easy to implement,and that the communication complexity of O(N)is achieved.

quantum private queries;quantum key distribution;communication complexity;database security;user privacy

TP918

A

1001-2400(2015)05-0033-05

2014-05-12< class="emphasis_bold">網絡出版時間:

時間:2014-12-23

國家自然科學基金資助項目(61372076);中央高校基本科研業務費專項資金資助項目(K5051301021,K5051301022);高等學校創新引智計劃資助項目(B08038)

賀小云(1977-),男,西安電子科技大學博士研究生,E-mail:thxy@msn.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.006.html

10.3969/j.issn.1001-2400.2015.05.006