利用二值描述符的實時目標跟蹤算法

覃 兵,田 軍,查宇飛,張立朝,黃宏圖

(空軍工程大學航空航天工程學院,陜西西安 710038)

利用二值描述符的實時目標跟蹤算法

覃 兵,田 軍,查宇飛,張立朝,黃宏圖

(空軍工程大學航空航天工程學院,陜西西安 710038)

針對目標跟蹤過程中的速率低和存儲量大的問題,提出了一種新的利用二值描述符特征的快速穩定的目標跟蹤算法.該算法首先在保持目標結構信息的情況下,通過尋找最優正交矩陣對樣本進行旋轉聚類,將樣本從歐式空間投影到漢明空間,生成二值描述符.然后在粒子濾波采樣的框架下,通過計算目標與候選樣本的漢明距離確定目標跟蹤位置.實驗結果表明,當發生光照、姿態變化和快速移動時,該算法跟蹤速度較快,并且能夠實現穩定跟蹤.

目標跟蹤;二值描述符;粒子濾波;漢明距離

如何利用特征描述符高效地建立目標的表示模型,是實現以目標檢測、跟蹤與識別為基礎的視覺任務系統的關鍵問題[1-4].在特征描述符發展初期,研究人員注重提高描述符的區分度,為獲得較高區分度的描述符,用一組實數向量對目標的各個關鍵點進行描述,稱這種特征描述符為實值描述符.尺度不變特征轉換(Scale Invariant Feature Transform,SIFT)特征[5]是實值描述符的典型代表,其對尺度、旋轉以及一定視角和光照變化等圖像的變化都具有不變性,并且SIFT具有很強的可區分性.但是,SIFT算法利用特征匹配的方法進行跟蹤時,由于需要對整幅圖片進行處理來提取特征,當圖像尺寸較大時,處理速度比較慢,無法達到實時性要求.

為了提高描述符生成和匹配的速度以及減小描述符所占存儲空間,產生了二值描述符[6].這類特征描述符用一組二值向量對目標進行描述,一般采用邏輯比較或者線性投影的方法生成,而匹配過程則用易于計算的漢明距離作為相似性度量.因此,這類特征描述符不僅所占存儲空間小,而且匹配速度快.

文獻[7]提出魯棒且獨立的二進制基本特征(Binary Robust Independent Elementary Features, BRIEF)二值描述符.它由128或256或512對比較組成,采樣點是按照中心位于特征位置的等方差高斯分布隨機選取的.BRIEF的計算量和存儲量低,但不具有尺度不變性和旋轉不變性.文獻[8]提出定向二進制特征(ORiented Brief,ORB)描述符,它解決了BRIEF缺少旋轉不變性的問題,并通過使用亮度質心ORB計算局部的方向.2013年,文獻[9]提出關鍵點二進制特征(BinBoost),設計了一個比較大的局部區域的二值描述符,通過構造二值哈希代價函數,利用推進方法(Boosting)獲得弱分類器集合及其權值,尋找最優的二值描述符.但是,上述算法都沒有考慮目標的整體結構信息,從而不能保持原來特征描述符在歐式空間的結構性.

基于以上考慮,筆者運用一種新的二值描述符生成算法,通過迭代量化的方法尋找最優正交矩陣對目標進行旋轉聚類,得到保持目標結構信息的哈希變換;將目標從歐式空間投影到漢明空間,且投影后的數據與歐式空間中的數據的相關性最大;降低了特征描述符的存儲空間,實現了快速匹配,充分利用速度和存儲優勢擴大了探索空間,提高了精度.

1 二值描述符的生成

新的二值描述符生成算法借鑒了文獻[10]的想法,通過迭代量化的方法尋找到最優的正交矩陣,將相似的樣本聚為一類,從而生成相同的二值描述符.該方法稱為迭代量化(ITerative Quantization,ITQ).

1.1 二值描述符的生成原理

如圖1所示,圖中每個點代表著一個樣本,假設這些樣本是通過主成分分析(Principal Component Analysis,PCA)降到二維后的顯示結果.當對這些樣本進行二值量化時,由圖1(a)可知,相似的樣本可能會量化到不同的二值描述符.如圖1(b)所示,通過樣本數據與一個隨機正交矩陣相乘可以使樣本發生一定的旋轉.因此,存在最優的正交矩陣,使得相似的樣本旋轉聚為一類,得到同樣的二值描述符,如圖1(c)所示.為此,文中將根據此想法生成目標的二值描述符,并運用到目標跟蹤中,充分發揮其準確性和有效性,將目標從歐式空間投影到漢明空間,保證投影后的數據與歐式空間中的數據的相關性最大.

圖1 樣本二值量化效果示意圖

1.2 二值描述符的生成方法

設有n個圖像樣本,每個樣本圖像維度為a×b,將每個圖像樣本數據作為一行,得到n個樣本對應的矩陣Xn×d,其中,n為樣本個數,d為每個樣本的維數,即d=a×b.要保證n個樣本的均值為0,即通過量化得到樣本的二值矩陣B∈{-1,1}n×k,其中,k為降維的維數.

首先,需要對上述n個樣本減少特征數,避免過度擬合,并最終降低存儲量.運用主成分分析(Principal Component Analysis,PCA)[11]的方法對樣本數據進行降維,設降維后樣本數據為Xn×k.

接下來,引入k×k維正交矩陣R,對Xn×k進行正交轉換,使得降維數據量化后的誤差最小,即

初始化隨機正交矩陣R,采用類似k均值[12]迭代量化方法尋找最小誤差.在每次迭代過程中,每個樣本通過符號函數的方法賦予二值矩陣B,然后更新正交矩陣R,不斷地使公式量化誤差最小,交替進行的步驟如下:

(1)固定R,更新B.根據式(1),得到

(2)固定B,更新R[10].對k×k矩陣BTV進行奇異值分解,即

其中,SVD代表奇異值分解.接著,得到正交矩陣

交替地更新B和R,是為了尋找最優的正交矩陣,從而使得量化的誤差越小.圖2顯示了隨著迭代次數的增加,量化誤差變化的過程.實驗結果表明,只要迭代80次就可以使得量化誤差趨于最小.

由以上步驟就能得到樣本的二值描述符.相對于實值描述符,生成二值描述符的方法不僅存儲量小,而且準確度高.

圖2 不同的迭代次數得到的量化誤差示意圖

2 利用二值描述符的實時目標跟蹤算法

基于上述新的二值描述符生成算法,文中的主要工作是將此新的方法運用到目標跟蹤上,在粒子濾波采樣框架下實現對目標的跟蹤.粒子濾波算法[13]是由當前幀的跟蹤結果在下一幀中得到對應的候選點,從而實現樣本的概率分布隨著時間的推移得到傳遞.

2.1 初始化

首先,在跟蹤圖像{Ii}i=1,2,…,N的第1幀I1中確定跟蹤目標,并由上述新的二值描述符生成算法計算目標的二值描述符.文中采用的是矩形框表示目標,設目標的初始位置P1=[x,y,w,h,θ],其中,(x,y)為跟蹤框的左上角坐標,(w,h)為跟蹤框的寬度和高度,θ為跟蹤框的旋轉角度.由此,可得到初始幀的跟蹤目標為

接著,生成目標的二值描述符.由上述新的二值描述符生成算法可知,單是由初始幀的跟蹤目標是無法得到二值描述符的,因此,需要在目標初始位置P1附近高斯采樣r個樣本,其中,r值過大或過小都會導致采樣的正負樣本個數不均衡,會對計算最優正交矩陣R產生影響,從而使得正負樣本無法映射得到不同的二值描述符,實驗結果表明,取r=300時效果最佳.高斯采樣參數Σ=[x′,y′,w′,h′,θ′],其中,(x′,y′)為跟蹤框x方向和y方向的移動范圍,(w′,h′)為跟蹤框的寬度和高度的收縮范圍,θ′為高斯采樣的旋轉角度.得到r個樣本如下:

其中,ITQ代表利用節1.2的迭代量化方法求解,k為下降的維數,m為迭代量化時的循環次數.得到了新的矩陣的二值描述符B(1+r)×k,取其第1行,也就得到了初始目標的二值描述符,即

同時,也得到了對數據降維的特征向量U,以及迭代量化m次后得到的最優正交矩陣R.這兩個參數將在接下來的跟蹤過程中使用.

圖3 利用二值描述符的實時目標跟蹤示意圖

2.2 跟蹤過程

算法流程如圖3所示.傳統的跟蹤算法由于其算法復雜度的影響,在采樣空間上范圍較小,如圖3第t+1幀采樣所示,這就可能會因目標的突然快速移動或姿態變化大而丟失目標.文中算法可以充分利用速度和存儲優勢,擴大搜索空間,增加候選采樣個數,進而能夠提高跟蹤精度.由上文得到了當前跟蹤目標的二值描述符,在下一幀中,通過粒子濾波的方法去采樣來得到候選樣本.設候選樣本個數為n,因此,可得到n個候選樣本為

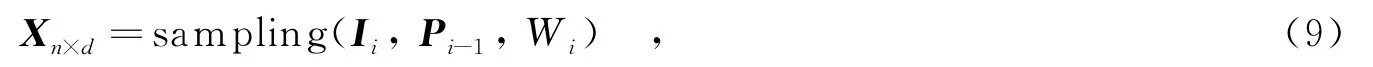
其中,sampling表示采樣.Ii為第i幀跟蹤圖像;Pi-1為第i-1幀跟蹤位置;Wi為粒子濾波采樣權值,并且設W2=Σ,即在第2幀時是通過高斯采樣得到候選樣本的.

得到了n個候選樣本后,通過新的二值描述符的生成算法計算出每個候選樣本的二值描述符.在此過程中,需要運用求初始目標二值描述符時得到的特征向量U和正交矩陣R,具體計算如下:

由此可以看出,目標跟蹤過程中候選樣本的二值描述符僅僅通過兩次乘法運算就可以得到,算法實現的速度較快,達到了目標跟蹤的實時性.

目標跟蹤中粒子的似然概率是通過計算粒子與目標模型之間的相似度或距離得到的,文中利用二值描述符和漢明距離度量方法來求取粒子的似然概率.由上述可知,目標的二值描述符為B0,n個候選樣本的二值描述符為Bn×k,則目標與候選樣本之間的漢明距離為

在文中,目標在下一幀的最終狀態由權重最大的粒子決定.所以,由Dn找出權重最大的粒子為

其中,Lindex表示權重最大的粒子位置,find表示找到權重最大的粒子.

2.3 更 新

在上述跟蹤過程中,最終得到了權值最大的候選樣本,進而可以得到此候選樣本對應的位置,作為跟蹤目標的位置更新可表示為

粒子濾波的核心思想是,用一組具有權值的粒子來完全表示后驗概率分布,即每個粒子的權重完全正比于其本身的似然概率.因此,得到上述n個候選樣本的權值為

其中,σ是觀測噪聲的標準方差.

最后,對目標的二值描述符進行更新,即

3 實驗結果及分析

文中所有實驗是在3.06 GHz,6 GB內存的64位計算機環境下,通過MATLAB 2013a軟件平臺仿真實現的.根據實驗跟蹤過程中的精確度和實時性考慮,樣本數據降維的維數k=64,候選樣本的個數n=500,高斯采樣參數Σ=[10,10,0.1,0.1,0.2],所有的3個測試視頻的參數及其描述如表1所示.

表1 視頻序列及其描述

3.1 實驗結果

為驗證文中算法,在對大量視頻序列進行跟蹤仿真實驗的基礎上,對基于領域分配法的目標跟蹤(Distribution Fields for Tracking,Track DF)[14]、基于魯棒且獨立二進制基本特征的目標跟蹤(Binary Robust Independent Elementary Features,BRIEF)以及文中算法(Proposed)的實驗結果和跟蹤性能進行分析,比較算法各自的復雜度.

圖4第1行是“Sylvester”部分結果.視頻中,背景比較相似、目標玩具姿態和移動速度不停變化.BRIEF的跟蹤結果與真實目標存在一定的位置偏差,尤其是目標發生姿態變化時,偏差也越大,如第596幀. Track DF能夠適應一定程度的姿態變化,但當姿態變化較大并且快速移動時,其跟蹤精度也隨之降低,如第996幀;而文中算法能夠至始至終對目標進行跟蹤.

圖4 “Sylvester”、“David”和“Dollar”跟蹤結果示意圖

圖4第2行是“David”部分結果.對其頭部跟蹤,主要有姿態、旋轉以及光照等變化,BRIEF的跟蹤結果在目標側身和取下眼鏡時存在較大的偏差,如第176幀和第346幀;Track DF在目標取下眼鏡時,也就是目標姿態發生較大變化時,丟失目標,如第346幀;文中算法雖然在目標側身過后存在一定的誤差,如第246幀,但偏差較小,能夠實現準確跟蹤.

圖4第3行是“Dollar”部分結果.可以看出,3種算法基本都能對目標至始至終的跟蹤.在目標產生折疊或者目標快速移動時,BRIEF產生的偏差相對于其他兩個算法較大,如第96幀、第176幀和第296幀.

3.2 性能分析

文中對照實驗所涉及的算法均按照原文獻所介紹的思路編寫,未進行任何形式的額外優化處理.下面對各算法的跟蹤性能以及算法復雜度進行簡要分析.

3.2.1 跟蹤性能

中心位置誤差[15]的計算表達式為

其中,O和Ot分別為算法得到的跟蹤框中心位置和目標真實中心點,中心位置誤差表示目標中心與真實目標中心的誤差,其值越小,表明跟蹤的精度越高.視頻中每幀的中心位置誤差如圖5所示,其中橫軸表示圖像幀數,縱軸表示均方根誤差.由圖5可知,文中算法要比其他兩種算法對目標有更準確的定位.

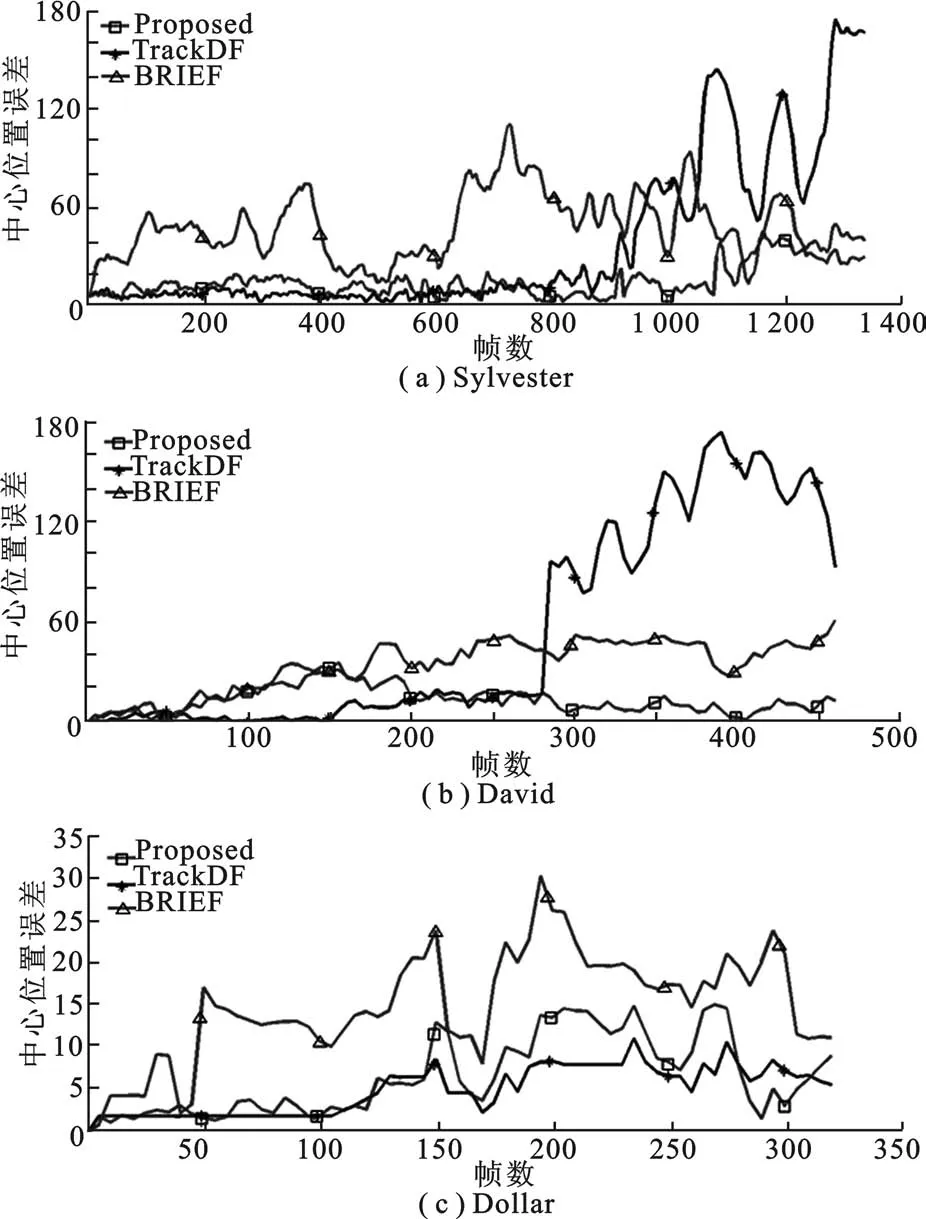
圖5 3種算法跟蹤結果的中心位置誤差比較示意圖

3.2.2 算法復雜度

Track DF算法首先對目標圖像按照灰度值區間進行分層;然后,對分層后的圖像分別進行空域和值域濾波,得到分布場特征;最后,用梯度下降法選取與目標圖像分布場特征之間歐式距離最小的候選位置為目標的跟蹤位置.因此,Track DF算法比BRIEF算法復雜,這里僅分析BRIEF算法與文中算法的復雜度.在BRIEF算法中,其構建二值描述符時,每個候選樣本都要經過nd次邏輯比較以及nd次加減運算,因此,BRIEF算法處理每一幀的算法復雜度為O(Nnd2).文中算法的復雜度主要在于式(10),因此,文中算法處理每一幀的復雜度為O(Ndk).表2給出了各算法平均每幀的處理時間.綜上可知,文中算法的處理速度最佳.

表2 3種算法的處理速度 s/幀

4 結束語

視覺跟蹤中如何利用特征描述符高效地建立目標的表示模型,一直是研究的熱點和難點.筆者通過對樣本二值描述符生成算法的研究,將一種新的二值描述符生成算法與粒子濾波相結合,提出了利用二值描述符的實時目標跟蹤算法.該算法通過迭代量化的方法尋找一個最優的正交矩陣,從而將樣本的數據進行旋轉聚類,使得相似的樣本能夠生成相似的二值描述符,尋找保持目標結構信息的哈希變換,使投影后的數據與歐式空間中的數據的相關性最大.并且文中充分利用速度和存儲優勢擴大探索空間,提高精度,因此新特征具有魯棒性的特點.通過粒子濾波算法,運用異或運算計算漢明距離,得到下一幀目標的位置以及后驗概率,提升了算法的速度和效率.將文中算法應用于視覺跟蹤領域,在跟蹤效果和跟蹤速度上都比其他跟蹤算法有所提高.

不足之處是,文中算法雖然在一定程度上解決了特征描述符表征特征的快速性和魯棒性的問題,但是降維時的特征向量和量化時的正交矩陣未能實時更新,因此,對于復雜背景的目標跟蹤效果仍不是十分理想.研究如何有效地在線更新特征向量以及正交矩陣,將大大增強文中算法的魯棒性,這將是下一步的工作.

[1]Li Xi,Hu W M,Shen C H,et al.A Survey of Appearance Models in Visual Object Tracking[J].ACM Transactions on Intelligent Systems and Technology,2013,4(4):58-72.

[2]李遠征,盧朝陽,李靜.一種基于多特征融合的視頻目標跟蹤方法[J].西安電子科技大學學報,2012,39(4):1-6. Li Yuanzheng,Lu Zhaoyang,Li Jing.Robust Video Object Tracking Algorithm Based on Multi-feature Fusion[J]. Journal of Xidian University,2012,39(4):1-6.

[3]孫浩,王程,王潤生.局部不變特征綜述[J].中國圖象圖形學報,2011,16(2):141-151. Sun Hao,Wang Cheng,Wang Runsheng.A Review of Local Invariant Features[J].Journal of Image and Graphics, 2011,16(2):141-151.

[4]高晶,畢篤彥,趙曉林.融合邊緣片斷與水平集分割的目標跟蹤算法[J].西安電子科技大學學報,2011,38(6):146-151. Gao Jing,Bi Duyan,Zhao Xiaolin.Non-rigid Object Tracking Based on the Boundary Fragment Feature and Level Set Segmentation[J].Journal of Xidian University,2011,38(6):146-151.

[5]Lowe D G.Object Recognition from Local Scale-invariant Features[C]//Proceedings of the Seventh IEEE International Conference on Computer Vision.Piscataway:IEEE,1999:1150-1157.

[6]Heinly J,Dunn E,Frahm J M.Comparative Evaluation of Binary Features[C]//Proceedings of the 12th European Conference on Computer Vision.Berlin:Springer,2012:759-773.

[7]Calonder M,Lepetit V,Strecha C,et al.BRIEF:Binary Robust Independent Elementary Features[C]//Lecture Notes in Computer Science:6314.Heidelberg:Springer Verlag,2010:778-792.

[8]Rublee E,Rabaud V,Konolige K,et al.ORB:an Efficient Alternative to SIFT or SURF[C]//Proceedings of the IEEE International Conference on Computer Vision.Piscataway:IEEE,2011:2564-2571.

[9]Trzcinski T,Christoudias M,Lepetit V,et al.Boosting Binary Keypoint Descriptors[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Washington:IEEE Computer Society,2013:2874-2881.

[10]Gong Y C,Lazebnik S.Iterative Quantization:a Procrustean Approach to Learning Binary Codes[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2011:817-824.

[11]Lauro N C,Verde R,Irpino A.Principal Component Analysis[J].Business Research Methods,2005,23(2):41-64.

[12]Huang Z.Extensions to the K-means Algorithm for Clustering Large Data Sets with Categorical Values[J].Data Mining and Knowledge Discovery,1998,2(3):283-304.

[13]張俊根,姬紅兵.采用粒子濾波和模糊聚類法的非線性多目標跟蹤[J].西安電子科技大學學報,2010,37(4):636-641. Zhang Jungen,Ji Hongbing.Passive Multi-target Tracking Based on Independent Particle Filtering and Fuzzy Clustering [J].Journal of Xidian University,2010,37(4):636-641.

[14]Sevilla-Lara L,Learned-Miller E G.Distribution Fields for Tracking[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.Washington:IEEE Computer Society,2012:1910-1917.

[15]Everingham M,Van Gool L,Williams C K,et al.The Pascal Visual Object Classes(VOC)Challenge[J].Interational Journal of Computer Vision,2010,88(2):303-338.

(編輯:齊淑娟)

Real-time visual object tracking based on binary descriptors

QIN Bing,TIAN Jun,ZH A Yufei,ZHANG Lichao,HUANG Hongtu
(Inst.of Aeronautics and Astronautics Eng.,Air Force Eng.Univ.,Xi’an 710038,China)

Object tracking often has the problems of low rate and high storage.Therefore,a tracking algorithm based on binary descriptors is proposed.The algorithm retains the original construction information on the samples and projects the samples from Euclidean space to Hamming space in order to generate binary descriptors by searching the optimal orthogonal matrix for rotating cluster.Then under the frame of particle filtering,it is necessary to determine the tracking position by computing the hamming distance.Analysis and experiment show that the proposed tracking algorithm performs rapidly and favorably when the target objects undergo large illumination,pose changes and fast movement.

object tracking;binary descriptors;particle filtering;hamming distance

TP391

A

1001-2400(2015)05-0168-07

2014-05-08< class="emphasis_bold">網絡出版時間:

時間:2014-12-23

國家自然科學基金資助項目(61472442);航空科學基金資助項目(20131996013)

覃 兵(1991-),男,空軍工程大學碩士研究生,E-mail:qinbingzaixian@163.com.

http://www.cnki.net/kcms/detail/61.1076.TN.20141223.0946.028.html

10.3969/j.issn.1001-2400.2015.05.028