索-鋼/鋁合金組合結構初始態確定及靜力分析

張莉

(上海大學土木工程系,上海 200072)

索-鋼/鋁合金組合結構初始態確定及靜力分析

張莉

(上海大學土木工程系,上海 200072)

索-鋼/鋁合金組合結構作為一種新穎的結構形式,是由拉索和壓桿(鋼管/鋁合金圓管)組成的自應力狀態下的穩定自平衡體系,體系中受拉連續,受壓不連續.在給定結構幾何外形和拓撲關系的基礎上,采用動力松弛法確定該體系的自應力初始態;在自重及外部荷載作用下,采用牛頓-拉弗森方法分析確定結構的靜力性能.為揭示此類結構的受力機理,該體系中的壓桿分別采用鋼管和鋁合金圓管,對比分析兩類組合結構在受力性能方面的異同.數值算例表明了本方法的實用性和優越性,為索-鋼/鋁合金組合結構在實際工程中的推廣應用奠定了基礎.

索-鋼/鋁合金組合結構;自應力初始態;力學性能

張拉整體體系是當今國際空間結構領域的前沿研究課題之一,被譽為“未來的結構體系”[1].該體系是一種由拉索和壓桿組成的自應力狀態下的穩定自平衡體系(以下簡稱為拉索/壓桿體系),體系中不連續受壓處于連續受拉的內部.

張拉整體體系所特有的建筑造型、結構形式和力學機理為土木工程師的設計提供了全新的靈感[1].這種體系的潛在優勢在于其自成一體,無需強大的下部支承結構,可覆蓋如膜、輕型屋面板等輕質屋面材料,從而極具經濟性,這就為會展場館、體育場館、機場候機樓等大跨度空間結構的設計提供了新思路和新技術.此外,張拉整體體系的應用范圍不局限于建筑領域,還可作為藝術雕塑以供觀賞,國外學者還將張拉整體的概念擴展到了其他領域如生物學領域中[1-2].

國內外學者的研究工作大多基于張拉整體基本單元或由基本單元拓展而成的張拉整體結構.我國學者對張拉整體體系的研究雖然起步較晚[3],但與國外的研究差距正在逐步縮小.就建筑領域而言,國內外學者的研究成果尚未被應用于大跨度屋蓋結構,這方面的工作還有待于進一步研究.

鋁合金結構、空間網格結構和索結構在我國逐步得到應用并已頒布相關規范[4-6].本研究在此基礎上,將張拉整體體系應用于索-鋼/鋁合金組合結構,其中的受拉單元采用鋼索,受壓單元分別采用鋼管和鋁合金圓管.通過數值方法來確定體系的自應力初始態及荷載態,揭示體系的受力機理,為該體系應用于工程實踐奠定理論基礎.

1 拉索-壓桿體系的自應力初始態確定

自應力初始態確定是指無自重狀態下的初始態確定,基于結構給定曲面/平面幾何及拓撲關系的力的平衡,不涉及結構本身的材料性能,可采用動力松弛法求解[7-9].

動力松弛法的基本思想是逐點(空間上)、逐步(時間上)跟蹤體系的動能,通過遞推方程求解.基于牛頓第二定律建立遞推方程,通過對時間點上虛擬動態過程的模擬來解決靜力問題.首先假定結構的初始曲面或平面幾何,可用有限單元來表示,本研究采用拉索/壓桿單元.假定結構的虛擬質量M集中在節點上,不平衡節點力激發結構運動,引起節點振蕩.節點振蕩隨著結構動能的逐步減小并趨于零而停止,此時可看作結構處于靜力平衡狀態.

t時刻空間任一點i在x方向的運動可直接由牛頓第二定律得到,以中心差分形式表示如下:

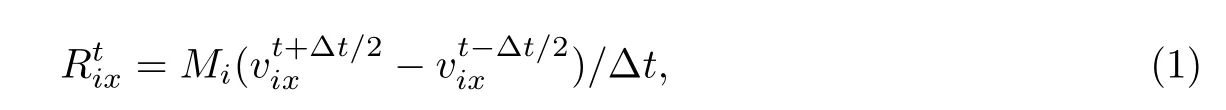
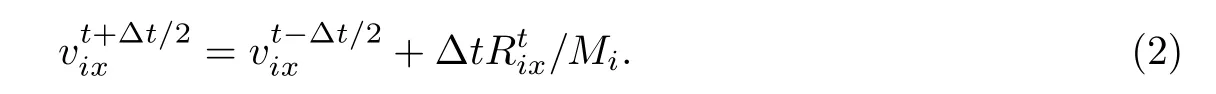
根據Barnes[7]給出的保證解收斂條件,取?t=1,得到

式中,Simax為節點i的最大可能剛度.對于拉索/壓桿單元,節點最大剛度Simax可由下式求得:

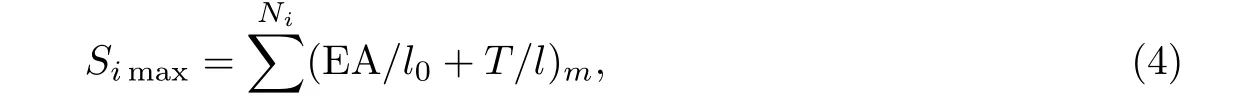
式中,Ni表示交匯于節點i的單元總數,EA為給定的單元軸向剛度,l0為單元m的無應力長度,l和T分別為單元m當前時刻的長度及內力.將式(3)代入(2)得到

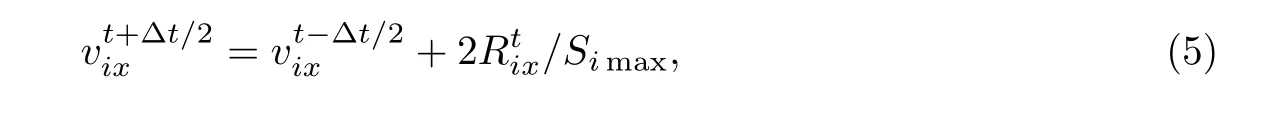
則t+?t時刻i節點的x坐標變為

根據新的節點坐標可求出各單元內力如下:

式中,Ts,ls分別為單元初始給定內力和長度.t+?t時刻節點不平衡力可由下式給出:

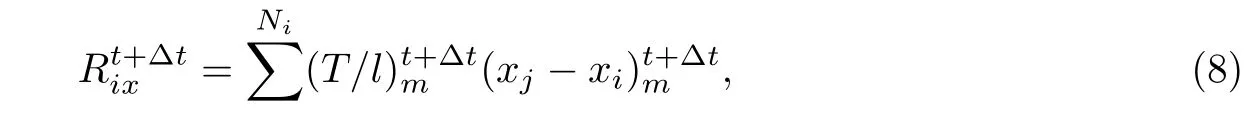
式中,與節點i相連的單元m的另一端為節點j.

計算步驟如下:

(1)假定體系的初始平面或曲面幾何及各單元的初始內力,通常情況下假定的內力分布不滿足節點平衡條件,此外將節點速度及結構動能設置為0;

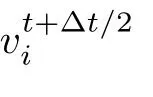
(5)重復步驟(2)～(4),直到節點不平衡力最大值滿足給定精度ε.每次迭代均需記錄結構動能E,若下一時刻的動能Et+?t/2小于前一時刻的動能Et??t/2,則體系的動能在t??t/2時刻達到極大值,此時將所有的速度分量設置為零,運動從t??t/2時刻重新開始.

2 拉索/壓桿體系荷載態的確定

荷載態的確定包含兩個階段的設計:第一階段僅考慮包含體系自重的荷載態確定,以下簡稱為第一荷載態;第二階段則在此基礎上,考慮外部荷載作用,以下簡稱為第二荷載態.

2.1 第一荷載態的確定

根據所確定的初始態,按照結構實際所采用的拉索、壓桿截面尺寸,求解體系在自重作用下的第一荷載態.考慮幾何非線性,可采用牛頓-拉弗森方法迭代求解非線性方程組[8,10],按i=1,2,3,…進行求解:

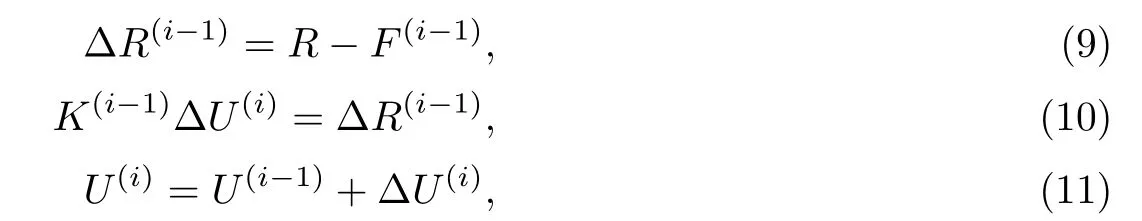
其中

式(9)～(11)中,R為作用于節點的外荷載,F(i?1)為等價于單元應力的第i?1次迭代的節點力向量,?R(i?1)為第i?1次迭代的不平衡荷載向量,K(i?1)為第i?1次迭代的切線剛度矩陣,?U(i)為第i次位移增量修正值,U(i)為第i次迭代的位移向量.

非線性方程(10)的求解還需考慮支座的約束條件,由于拉索/壓桿體系為穩定的自應力體系,因此對于各支座節點可僅考慮由自重引起的豎向約束.

對于拉索/壓桿單元,軸力T可由下式求得:

式中,l0為單元的初始放樣長度,l為當前位置單元長度,EA為單元的實際軸向剛度.單元切線剛度矩陣[kT]為6×6矩陣:

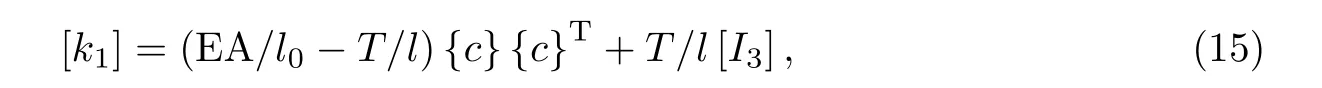
式中,[I3]為3×3單位矩陣,{c}為當前位置的單元方向余弦,可表示為

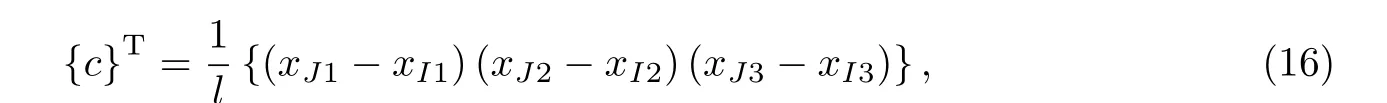
其中I,J為單元的兩端節點編號,xI1,xI2,xI3為節點I的空間位置三維坐標.

一個有效的以迭代法為基礎的增量解法,必須為終止迭代而采用現實可行的準則. Bathe[10]給出了3種常用的收斂準則.

(1)位移準則:

式中,εD為預定位移收斂限值,表示第i步位移增量的2范數在總位移向量的2范數的預定限值之內.

(2)殘余力準則:

式中,εF為預定殘余力限值,表示殘余力向量的2范數在荷載向量的2范數的預定限值之內. (3)能量準則:

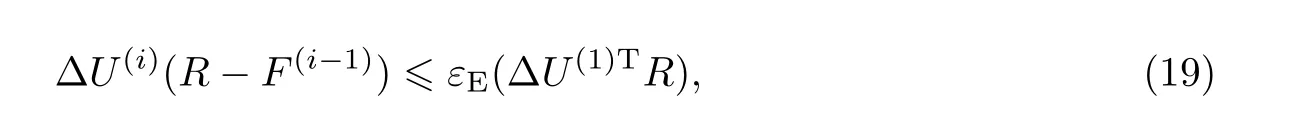
式中,εE為預定能量限值,表示每次迭代時內能增量(即在位移增量上不平衡荷載所做功的大小)的2范數在初始內能增量的2范數的預定限值之內.

2.2 第二荷載態的確定

在僅考慮體系自重的第一荷載態已確定的基礎上,考慮外部荷載作用,采用牛頓-拉弗森法迭代求解,此時支座的約束條件依照結構的實際支座約束而定.

3 應用算例

作為理論應用,本研究給出一個數值算例.圖1為依據莫特羅[1]給出的“微型網格”所設計的平板型雙層拉索/壓桿體系,圖中以較粗實線表示壓桿,以較細實線表示拉索.拉索在上、下層及層間均有布置,受拉連續;壓桿僅在層間有布置,受壓不連續.鑒于該體系雙軸對稱,圖中僅給出了1/4網格的節點編號.與“微型網格”相比,圖1所示體系增加了上層索2-4,1-3和下層索8-11,7-9.

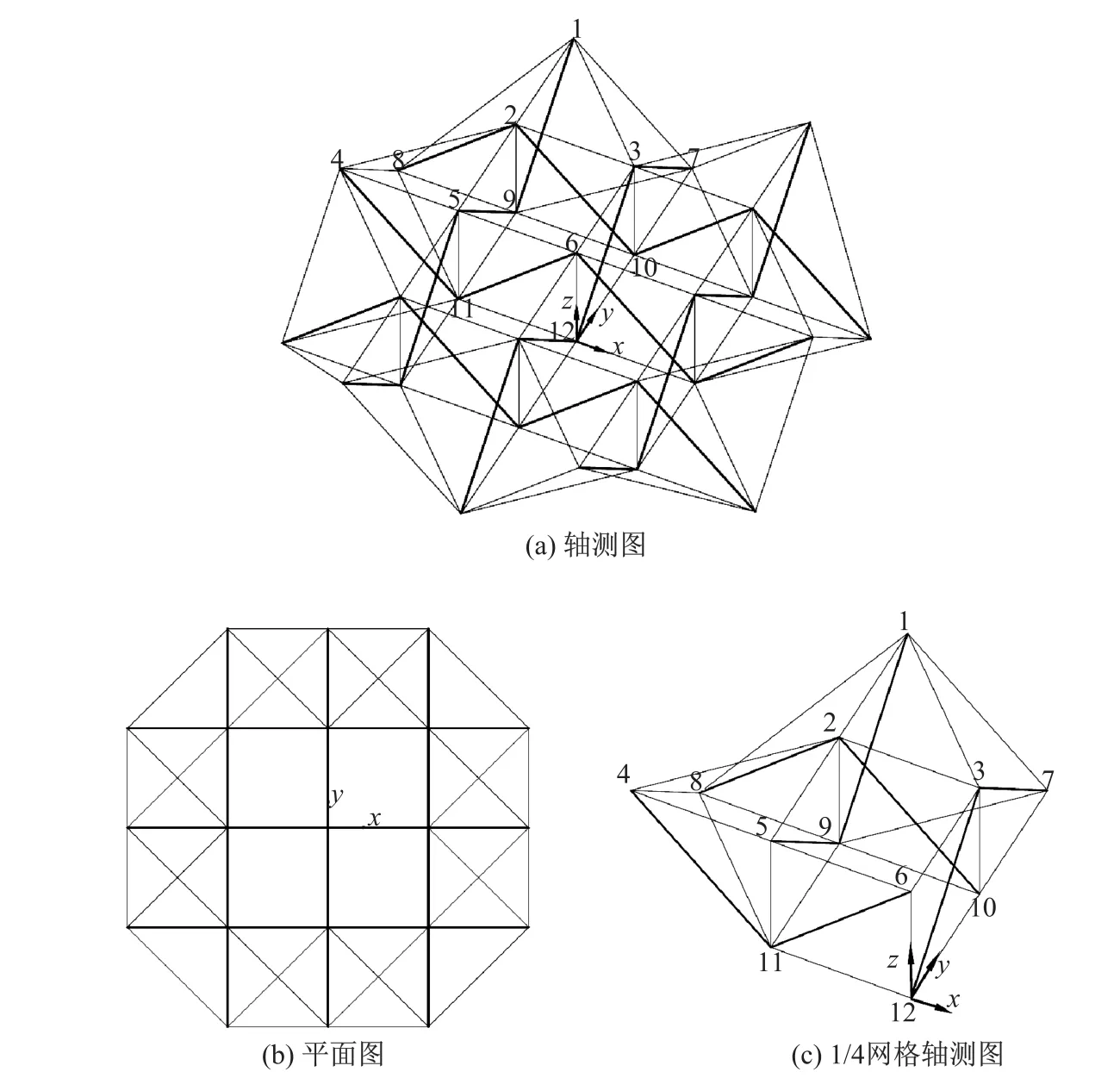
圖1 拉索/壓桿體系Fig.1 Cable-strut system

與節點編號相對應的拉索、壓桿單元的初始給定長度如表1～4所示,其中所有壓桿的初始給定長度均相同(2 262.742 mm),所有與坐標軸方向一致的層間垂直索(2-9,3-10,5-11, 6-12)及上、下層索的長度均相同(1 600.000 mm).

首先需確定體系的初始態,計算中假定所有單元的軸向剛度EA=1.0×106,節點不平衡力最大值滿足給定精度ε=1.0×10?6,所有壓桿的初始給定內力為?30.000 kN(壓為負),所有拉索的初始給定內力為30.000 kN(拉為正).采用動力松弛法求得各單元在初始態的內力及長度如表1～4所示.由表可見,體系的內力分布比較均勻,其中壓桿的內力分布在?32.384～?34.909 kN之間;上、下層索單元的內力有較大差別,在2.526～10.068 kN之間;層間垂直索的內力分布在47.021～48.244 kN之間;層間斜索的內力分布在16.192～22.924 kN之間.

采用索-鋼組合和索-鋁合金組合分別確定體系的第一荷載態,區別在于壓桿分別采用鋼管和鋁合金圓管.計算中考慮節點自重,節點采用螺栓球節點BS100[11],拉索采用鋼絲繩結構1×37[12],鋼管采用焊接鋼管[13],鋁合金圓管采用弱硬化鋁合金擠壓無縫圓管(牌號6061;狀態T6)[4,14],壓桿、拉索的截面尺寸如表1～4所示.由于體系屬于自應力作用下的自平衡體系,參考現行《空間網格結構技術規程》[5],網架可采用上弦或下弦支承方式,計算中假定僅在上層外節點處(對應于1/4網格的節點1,4)有豎向固定支承,即支座節點僅承受體系的豎向自重.無需如索網、索膜等預應力體系所需的強大水平支承,這也是自應力體系與預應力體系相比具有的一大優勢.

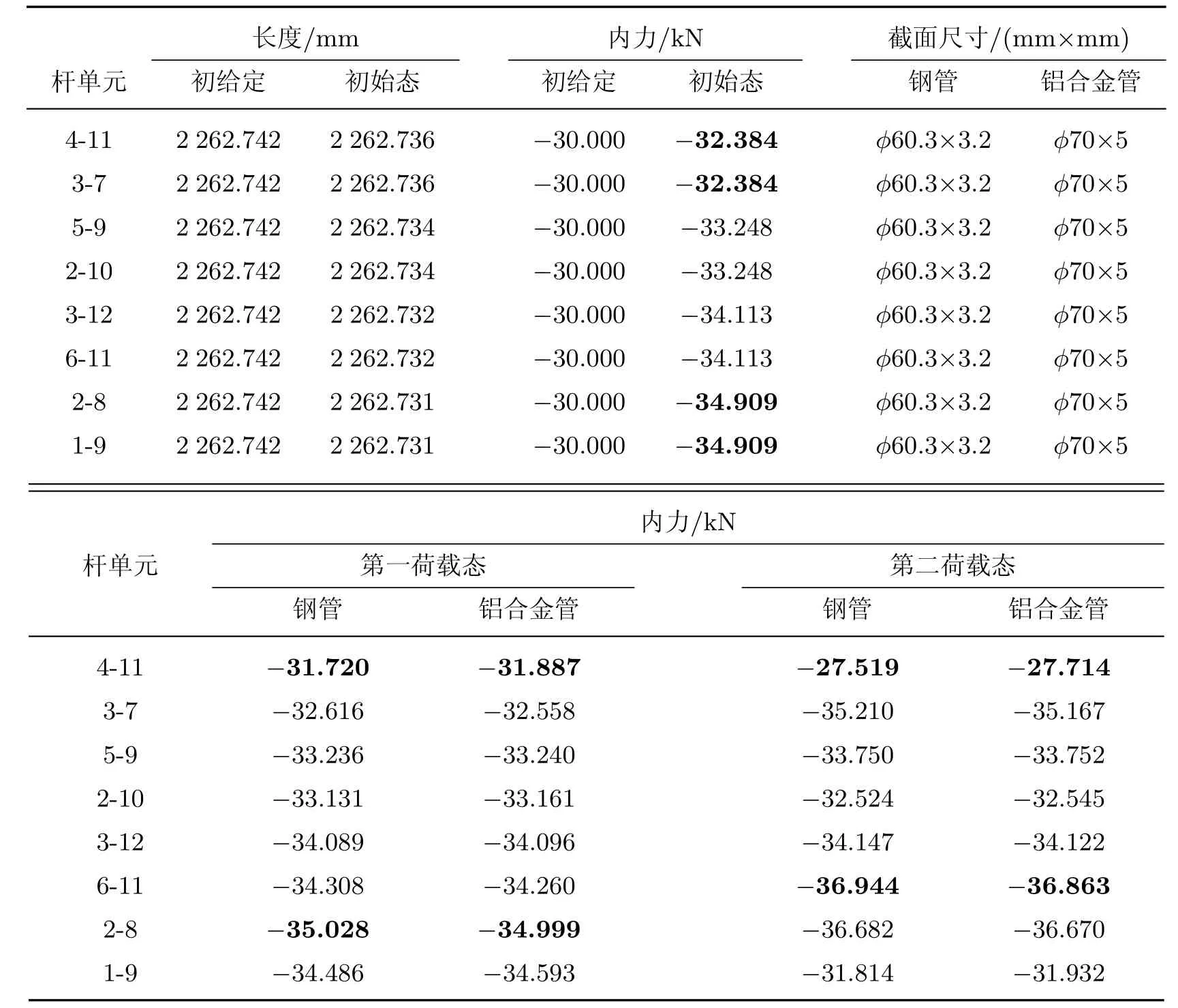
表1 初始態與荷載態桿單元長度及內力Table 1 Element forces and lengths of struts in initial and load states

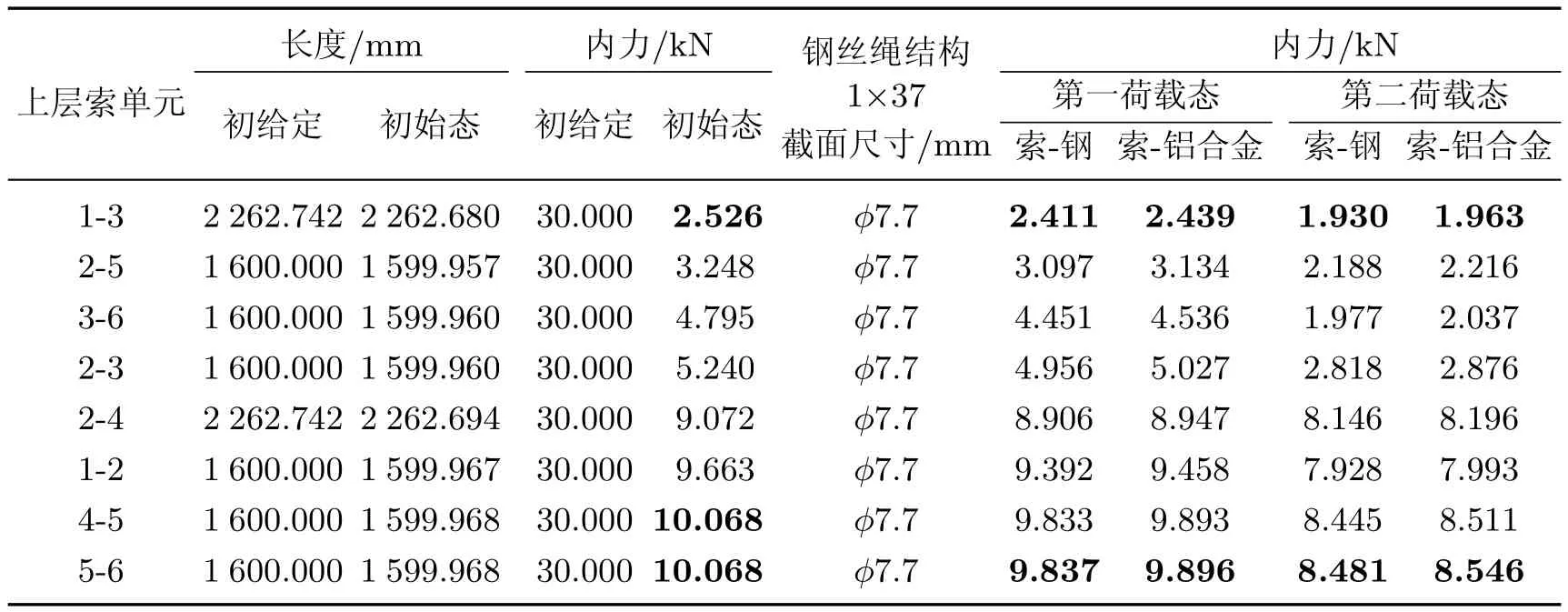
表2 初始態與荷載態上層索單元長度及內力Table 2 Element forces and lengths of upper layer cables in initial and load states

表3 初始態與荷載態下層索單元長度及內力Table 3 Element forces and lengths of lower layer cables in initial and load states

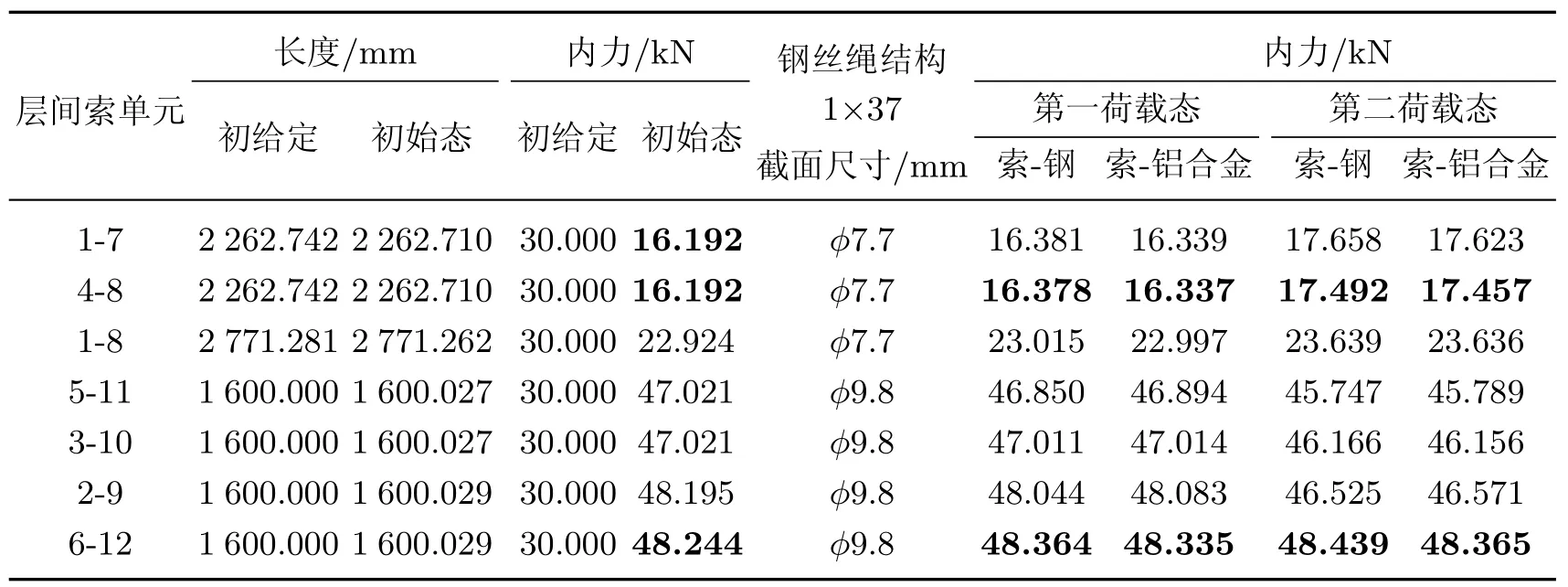
表4 初始態與荷載態層間斜索和垂直索單元長度及內力Table 4 Element forces and lengths of diagonal/vertical cables in initial and load states

對于第一、第二荷載態,計算中的收斂準則同時以位移準則、殘余力準則和能量準則來控制,分別取εD=1.0×10?3,εF=1.0×10?6,εE=1.0×10?8.對于鋼材取彈性模量E=2.06× 105N/mm2[15],對于拉索(單股鋼絲繩)取E=1.4×105N/mm2[6],對于鋁合金取E=7.0× 104N/mm2[4].

第一荷載態中各單元的內力如表1～4所示,從表中可以看出,當壓桿分別采用鋼管和鋁合金圓管時,體系在自重作用下的內力分布差別不大.而且由初始態到第一荷載態體系的最大豎向位移均為中心節點12(索-鋼組合:?0.587 mm;索-鋁合金組合:?0.449 mm);豎向支座反力也都不大(索-鋼組合:節點1為0.588 kN,節點4為0.840 kN;索-鋁合金組合:節點1為0.453 kN,節點4為0.644 kN),主要原因在于體系在初始態已具有較大剛度.此外,盡管拉索、壓桿在初始態都具有較大的內力,但它們是自平衡的,各支座僅承受體系的自重,這也使得該體系與預應力體系(如索網、索膜、索穹頂等)相比具有較大優勢.

在第一荷載態確定的基礎上,第二荷載態[6,16]考慮輕型屋面板,自重取0.3 kN/m2,屋面活荷載為0.5 kN/m2.本研究考慮荷載基本組合為1.0×自應力+1.2×恒載+1.4×活載,以及荷載標準組合為1.0×自應力+1.0×恒載+1.0×活載(用于計算體系撓度).計算中假定在上層外節點處(對應于1/4網格的節點1,4)有豎向固定支承,水平向為彈性支承,彈簧剛度為0.5 kN/mm.

第二荷載態體系的最大豎向位移均為中心節點12(索-鋼組合:?3.323 mm;索-鋁合金組合:?3.381 mm).索-鋼組合體系的豎向支座反力:節點1為5.547 kN,節點4為7.197 kN;索-鋁合金組合體系的豎向支座反力:節點1為5.418 kN,節點4為6.990 kN.第二荷載態各單元的內力如表1～4所示,從表中可看出,體系在第二荷載態仍具有較強的抵抗外部荷載的能力,除少數自應力值較小的上、下層索外,無論是拉索還是壓桿,其內力的變化幅度相對于自應力都不大,僅有小幅度的增減,這也表明了這種自應力體系的優越性.一旦確定了初始態,體系就具有了較大的初始剛度和較強的抵抗外部荷載的能力.

從索-鋼組合和索-鋁合金組合的對比中可以看出,鋁合金的彈性模量僅為拉索的1/2,接近于鋼材的1/3;鋼材的質量密度ρ=7 850 kg/m3,鋁合金的質量密度ρ=2 700 kg/m3,也接近于鋼材的1/3.本算例中,整個模型水平投影面積為35.84 m2,鋼制螺栓球節點的自重為197.3 kg,鋼絲繩索的自重為43.5 kg,鋼管的自重為244.7 kg,鋁合金圓管的自重為149.7 kg,不足鋼管自重的62%.索-鋼組合體系總重485.5 kg,耗鋼量不足14 kg/m2;索-鋁合金組合體系總重390.5 kg,耗鋼量不足11.0 kg/m2.如果體系的節點采用鋁合金螺栓球節點[17],則體系的自重將有進一步較大幅度的減輕.

無論是在第一荷載態還是第二荷載態,索-鋼組合體系和索-鋁合金組合體系的最大撓度及單元內力分布都差別不大,這表明鋁合金材料比鋼材更具有輕質高強的優勢.特別是隨著跨度的增大,當體系自重的影響越來越大時,采用鋁合金材料的優勢將更加明顯.

上述算例表明,采用動力松馳法確定體系初始態,以及采用牛頓-拉弗森法確定體系荷載態具有實用性和優越性,為索-鋼/鋁合金組合結構在實際工程中的推廣應用奠定了基礎.

4 結論

(1)索-鋼/鋁合金組合結構是由拉索和壓桿(鋼管/鋁合金圓管)組成的自應力狀態下的穩定自平衡體系.體系的自應力初始態可采用動力松弛法來確定,在僅考慮體系自重的第一荷載態和有外部荷載作用的第二荷載態的情況下,需考慮幾何非線性的影響,可采用牛頓-拉弗森法通過迭代求解非線性方程組來確定荷載態結構幾何與內力分布.

(2)索-鋼組合結構和索-鋁合金組合結構的受力機理相似,在初始態由于自應力的存在,體系均具有較大的剛度;在第一荷載態,支座節點僅承受體系的自重作用;在第二荷載態,各單元的內力與自應力相比變化幅度不大,表明體系具有較好的抵抗外部荷載的能力.

(3)索-鋼/鋁合金組合結構具有自重輕、受力性能好和支座負擔輕的優點;與索-鋼組合結構相比,索-鋁合金組合結構可進一步減輕體系自重,這在大跨度結構中更具優勢.

[1]莫特羅.張拉整體——未來的結構體系[M].薛素鐸,劉迎春,譯.北京:中國建筑工業出版社,2007: 7-30,197-226.

[2]Stamenovic D.Effects of cytoskeletal prestress on cell rheological behaviour[J].Acta Biomaterialia,2005,1(3):255-262.

[3]劉錫良,陳志華.一種新型空間結構——張拉整體體系[J].土木工程學報,1995,28(4):52-57.

[4]中華人民共和國建設部.GB 50429—2007鋁合金結構設計規范[S].北京:中國計劃出版社,2008.

[5]中華人民共和國住房和城鄉建設部.JGJ 7—2010空間網格結構技術規程[S].北京:中國建筑工業出版社,2010.

[6]中華人民共和國住房和城鄉建設部.JGJ 257—2012索結構技術規程[S].北京:中國建筑工業出版社,2012.

[7]Barnes M R.Form-finding and analysis of prestressed nets and membranes[J].Computers and Structures,1988,30:685-695.

[8]張莉.張拉結構形狀確定理論研究[D].上海:同濟大學,2000.

[9]Zhang L,Maurin B,Motro R.Form-finding of nonregular tensegrity systems[J].ASCE Journal of Structural Engineering,2006,132(9):1435-1440.

[10]Bathe K J.Finite element procedures[M].New Jersey:Prentice-Hall,1996:754-765.

[11]中華人民共和國住房和城鄉建設部.JG/T 10—2009鋼網架螺栓球節點[S].北京:中國標準出版社,2009.

[12]中國鋼鐵工業協會.GB/T 20118—2006一般用途鋼絲繩[S].北京:中國標準出版社,2006.

[13]中國鋼鐵工業協會.GB/T 21835—2008焊接鋼管尺寸及單位長度重量[S].北京:中國標準出版社, 2008.

[14]全國有色金屬標準化技術委員會.GB/T 4436—2012鋁及鋁合金管材外形尺寸及允許偏差[S].北京:中國標準出版社,2013.

[15]中華人民共和國建設部.GB 50017—2003鋼結構設計規范[S].北京:中國計劃出版社,2003.

[16]中華人民共和國住房和城鄉建設部.GB 50009—2012建筑結構荷載規范[S].北京:中國建筑工業出版社,2012.

[17]上海市工程建設標準化辦公室.DGJ08—95—2001鋁合金格構結構技術規程(試行)[S].上海:上海市工程建設標準化辦公室,2001.

Initial state determination and static analysis of composite cable and steel/aluminum structures

ZHANG Li
(Department of Civil Engineering,Shanghai University,Shanghai 200072,China)

Composite cable and steel/aluminum structure is a new system.It is in a selfstress and stable self-equilibrated state,comprising a continuous set of tension members (cables)and a discontinuous set of compression components(steel pipes or alloy tubes). Starting from an initial specified geometry and topology,the initial self-stress is determined using a dynamic relaxation method.The behavior of the structure is analyzed for safely resisting the self-weight and applied static load using the Newton-Raphson method.To understand its mechanical property,steel pipes and alloy tubes are used as compression members respectively in the two kinds of composite structures.Application of the process is shown with a numerical example.It is concluded that that improvement in engineering application of the composite cable and steel/aluminum structure has been achieved.

composite cable and steel/aluminum structure;initial self-stress state;mechanical property

TU 398.9

A

1007-2861(2015)05-0631-09

10.3969/j.issn.1007-2861.2014.05.009

2014-10-10

上海大學創新基金資助項目(10011811001)

張莉(1969—),女,副教授,博士,研究方向為空間結構.E-mail：l.zhang@shu.edu.cn