電源輸出功率最值問題的應用

王偉民 畢 亮

（1.太和縣宮集鎮中心學校，安徽 阜陽 236652；2.綠春縣第一中學，云南 紅河 662599）

由于電源有內阻，在電源電動勢一定的情況下，由純電阻元件組成的電路，當外電路電阻由某一數值逐漸減小，甚至降為0時，電路中的總電流不可能因外電路電阻的減小而變得無窮大，而是趨于某一數值.由公式P＝I2R可知，外電路消耗的電功率（亦即電源的輸出功率）不可能因電流的增大而變得無窮大.可以證明，當外電路電阻等于電源內阻時，電源的輸出功率達到最大值.

證明：如圖1所示的純電阻電路，設電源電動勢為E，內阻為r，滑動變阻器接入電路中的電阻為Rx時，電源的輸出功率為Px，則有

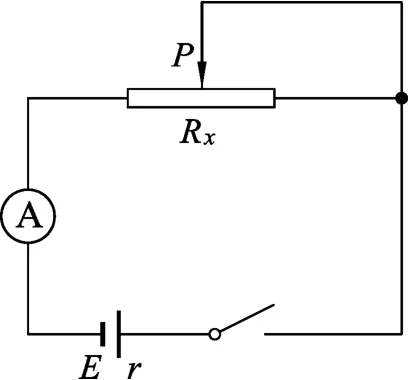
圖1

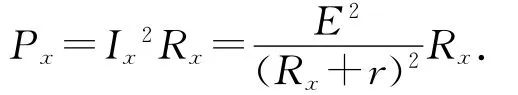
以下為該結論的一個應用.

例1.如圖2所示的電路，電源電動勢E＝6V，內阻r＝1Ω，保護電阻R0＝3Ω，滑動變阻器總電阻R＝20Ω，閉合開關S，在滑片P從a滑到b滑動的過程中，滑動變阻器消耗總功率的變化規律是

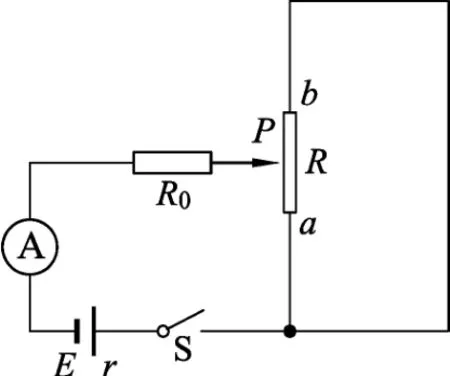
圖2

（A）先減小，后增大.

（B）先增大，后減小.

（C）先減小后增大，再減小，再增大.

（D）先增大后減小，再增大，再減小.

解析：解決此類問題的常規思路是，求出滑動變阻器消耗的電功率跟滑動變阻器Pa段電阻間的函數關系式，根據函數值的變化情形來判斷滑動變阻器消耗功率的變化情形.我們不妨先運用該方法進行求解.由圖2可知，整個電路的連接方式為，滑動變阻器Pa、Pb兩部分并聯之后，再和保護電阻R0串聯.

設RPa＝x，滑動變阻器連入電路的等效電阻Rx為

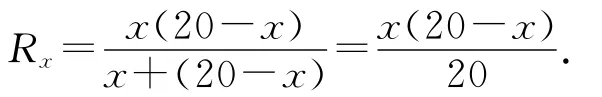
則有

兩邊對y求導得

令P′＝0，得y＝±80.（80舍去，保留－80，原因是x2－20x為負數）

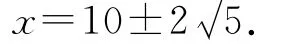
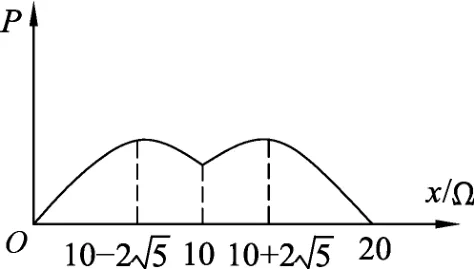
圖3

如果是考試，對于一道選擇題，花費如此大的功夫，即使做了出來，也顯得不“劃算”——對函數

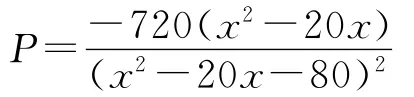
采用換元法求導，繼而又解方程確定函數駐點，過程非常麻煩（如果不換元，直接求導，會更麻煩），解題過程會花費相當長的時間.那么，有沒有簡便方法呢？

實際上，我們可以根據電源輸出功率的最大值規律來進行求解.

圖2中，將r＋R0＝4Ω作為一個整體，并視為電源的“內阻”，所以，當滑動變阻器總電阻的阻值等于電源“內阻”4Ω時，滑動變阻器消耗的功率最大，由于滑動變阻器總電阻Rx與Pa段電阻x間的函數關系式

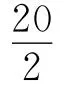
可以看出，這種解題過程，除了滑動變阻器兩并聯部分的最大等效電阻需要計算外（而且是非常簡單的計算，口算即求出結果），整個判斷過程無需動筆計算，解題過程顯得干凈利索，簡潔明快.

當然，對該題而言，如果題目條件改變一下——滑動變阻器的阻值小于或等于（r＋R0）的4倍時（即不超過16Ω），比如滑動變阻器的阻值為12Ω，在滑片由a至b滑動過程中，滑動變阻器兩部分并聯的總電阻增大到最大值3Ω時（大小等于滑動變阻器阻值的1/4），滑片位置在變阻器線圈的正中間，在這一過程中，變阻器消耗的總功率一直增大，此后，滑片P由中間位置向上繼續滑動時，滑動變阻器兩部分并聯的總電阻減小，所以，滑動變阻器消耗的總功率也跟著減小，該選擇題答案選項將由原來的（D），變為現在的（B）即滑動變阻器消耗總功率的變化規律為先增大，后減小.