巧用摩擦角解力學中的摩擦臨界極值問題

黃 偉

（湖北漢川一中，湖北 漢川 431600）

用摩擦角結合圖示分析求解力學中的摩擦臨界極值問題較簡單.

1 基本概念和規律

1.1 摩擦角

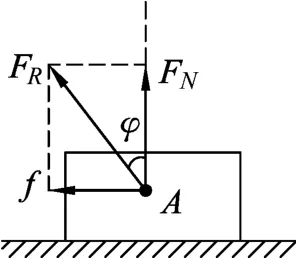
圖1

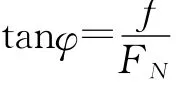
1.2 自鎖現象

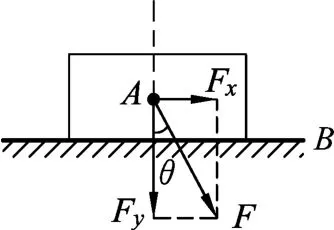
圖2

如圖2可得，若沿與法線成角θ≤φ的方向對A物體施力F推它，則該力沿A、B接觸面切線方向的分力大小Fx＝Fsinθ＝Fytanθ，其中Fy為F沿法線方向的分量，以FN表示B對A的支持力，fm表示A、B間的最大靜摩擦力，在FN≥Fy的情況下，有Fx＝Fytanθ＜FNtanφ＝fm.

表示無論F多大，都不能使A、B間發生相對滑動，這一現象叫“自鎖現象”.

同理可證明：豎直面和傾斜面上產生自鎖的條件和水平面的情況相同.

2 基本概念和規律的應用

2.1 自鎖中的臨界問題

在靜摩擦因素μ一定的情況下，實現自鎖有以下兩種途徑.

（1）通過控制力的方向而自鎖.

例1.（2012年高考課標卷24題）拖把是由拖桿和拖把頭構成的擦地工具（如圖3）.設拖把頭的質量為m，拖桿質量可以忽略；拖把頭與地板之間的動摩擦因數為常數μ，重力加速度為g，某學生用該拖把在水平地板上拖地時，沿拖桿方向推拖把，拖桿與豎直方向的夾角為θ.

（1）若拖把頭在地板上勻速移動，求推拖把的力的大小.

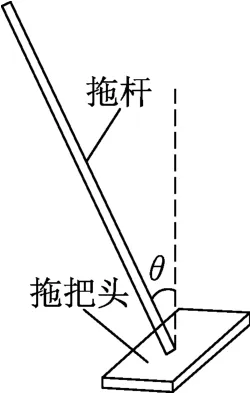
圖3

（2）設能使該拖把在地板上從靜止剛好開始運動的水平推力與此時地板對拖把的正壓力的比值為λ.已知存在一臨界角θ0，若θ≤θ0，則不管沿拖桿方向的推力多大，都不可能使拖把從靜止開始運動.求這一臨界角的正切tanθ0.

解析：（1）由題意易知，

（2）常規解法：

聯立（1）～（3）式得

當F無限大時右式極值為0，則

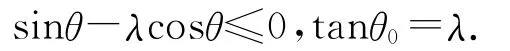
摩擦角解法：由題意，剛好開始運動時的水平推力等于此時拖把受到的最大靜摩擦力fm，則比值λ即為拖把頭與地板間的靜摩擦因數，臨界角θ0即為靜摩擦角φ，設地板對拖把的正壓力為FN，由自鎖現象的結論則可得

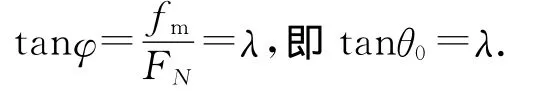
（2）通過控制傾斜面的方向而自鎖.

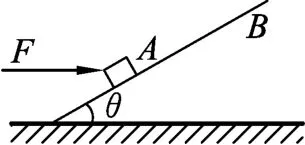
圖4

例2.如圖4所示，質量為m的物體放在斜面上，當斜面傾角θ為30°時恰能沿斜面勻速下滑.保持θ為30°，對物體施加一水平向右的恒力F，使物體沿斜面勻速向上滑行（設最大靜摩擦力等于滑動摩擦力）.增大θ，當θ超過某一臨界角θ0時，則不論水平恒力F多大，都不能使物體沿斜面向上滑行，已知重力加速度為g，試求：

（1）物體與斜面間的動摩擦因數μ.

（2）這一臨界角θ0的大小.

（2）如圖5，設物體具有沿斜面上滑的趨勢，F與法線間的夾角為α，摩擦角為φ，物體受4個力，即F，mg，FN，f.則

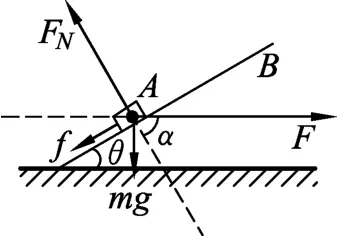
圖5

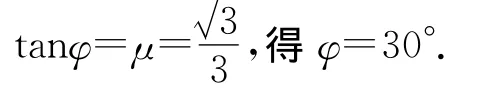
由自鎖現象的結論可得當α≤φ＝30°時，不論水平恒力F多大，都不能使物體沿斜面向上滑行，由幾何關系可得

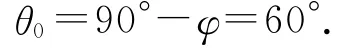
2.2 平衡中的極值問題

此類問題分水平面和傾斜面上求極值兩種情況，方法同理，在此以水平面為例.

例3.如圖6所示，在水平地面上放有一質量為m的物體，它與地面動摩擦因數為μ，現對物體施加一拉力F，使其沿地面勻速直線運動，求F的最小值及方向.

解析：如圖7所示，設F與水平面夾角為θ，摩擦角為φ，物體受4個力，即mg、F、FN、f，合力為0.如圖8所示，mg一定，由摩擦角的知識可知FN與f的合力FR方向一定，則F與FR垂直時F最小.即

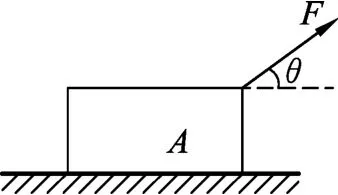
圖6

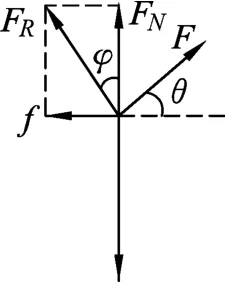
圖7

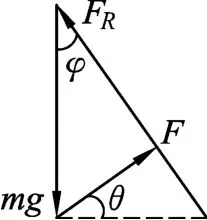
圖8

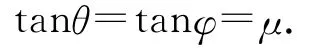
2.3 勻變速直線運動中的極值問題

此類問題同樣分水平面和傾斜面上求極值兩種情況，方法同理，在此以傾斜面為例.

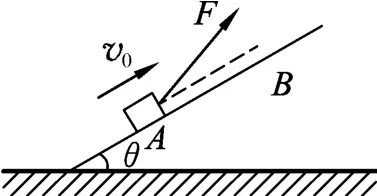
圖9

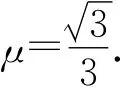
（1）求物塊加速度的大小及到達B點時速度的大小.

（2）拉力F與斜面的夾角多大時，拉力F最小？拉力F的最小值是多少？

解 析：（1）由題意易知，

（2）常規解法：設F與斜面間夾角為α，物塊受力如圖10所示，則

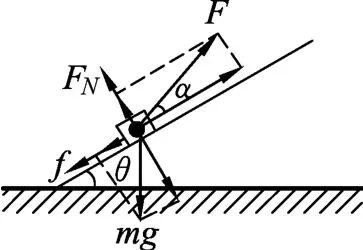
圖10

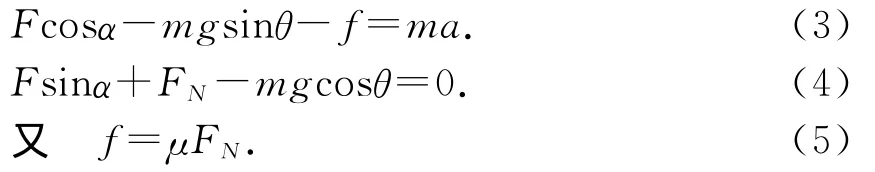
聯立（3）～（5）式得

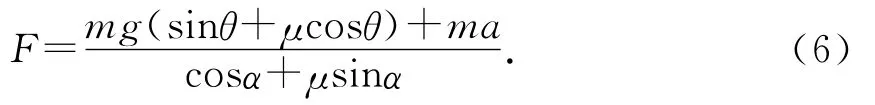
由數學知識得

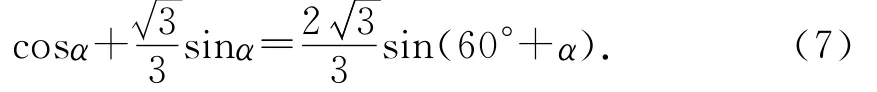
摩擦角圖解法：物塊受力如圖11所示，合力為F合＝ma，方向沿斜面向上.由摩擦角的知識可知：拉力F方向改變，摩擦角φ不變，即FN與f的合力FR方向一定，有

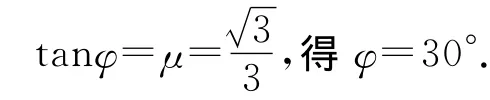
力的合成如圖12所示，當F與FR垂直時，F最小.由幾何關系易得

α＝φ，即α＝30°.

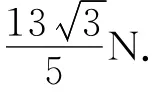
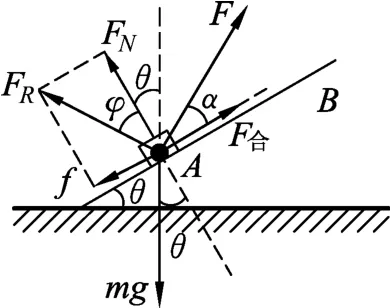
圖11

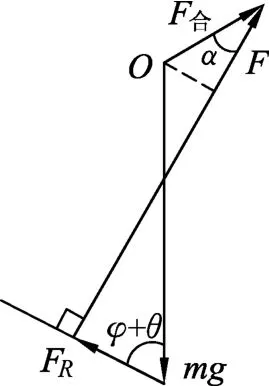
圖12

此類平衡和勻變速直線運動中有摩擦力的極值問題，都可用摩擦角圖解法，尤其是在4個力的作用下求F的最小值，引入摩擦角可將4個力等效為3個力來處理，這3個力中，FR方向定，另一個力大小方向定，則第3個力F與FR垂直時最小.

由此可見，解此類摩擦臨界極值問題，摩擦角的圖解法與函數求極值相比，物理意義更加明確，通俗易懂.