多孔介質冰蓄冷板的融化過程

劉小平，蔣玉龍，張素軍，李菊香

（1南京工業大學產業處，江蘇 南京 211816；2南京工業大學能源學院，江蘇 南京 211816）

相變儲能是利用相變介質進行相變潛熱的釋放或儲存的技術[1]，因具有潛熱量大、相變過程等溫等優點，越來越受到人們的重視。相變材料在電力“移峰填谷”、太陽能熱利用、建筑節能等工業或民用領域廣泛應用[2-4]。開孔泡沫金屬因具備優良的熱力、力學性能，已被應用于填料、緊湊型熱交換器等的制造[5-6]。將高導熱性能的開孔泡沫金屬填充入相變介質，可提高復合相變材料的綜合導熱性能，改良相變儲能過程[7-9]。Siahpush 等[10]研究表明，在純度為99%正二十烷的中填充孔隙率95%的泡沫銅，能將復合材料熱導率從0.423W/(m·K)提升到3.06W/(m·K)。吳志根等[11]實驗研究結果表明：泡沫金屬和膨脹石墨能有效提高高溫相變蓄熱系統的換熱能力。高導熱性能多孔介質的孔隙參數會對相變過程產生影響。王杰利等[12]研究認為，孔隙率對相變熱阻具有較大影響，適當減小孔隙率可有利于增強熱傳導。楊秀等[13]模擬研究發現，泡沫鋁的孔隙率越小，融冰所需時間越少，蓄冰球的有效容積也越小。Shiina 等[14]研究認為，多孔泡沫金屬的最佳孔隙率隨蓄熱系統傳熱系數的增加而有所降低。

對于相變介質中填充高導熱性能的多孔介質以縮短相變時間的研究，很多學者已做了大量的工作。然而實際過程中，部分相變介質自身的熱導率已經滿足要求，需要的是通過延長相變時間來控制相變過程的釋冷速率。如采用復合材料制成冰蓄冷板滿足某些制冷設備的需求。對于將低導熱性能的多孔介質填充入固液相變介質構成復合相變材料、延長相變時間的研究鮮見報道。為此，本文提出了在純冰中填充導熱性能相對較低的網狀聚氨酯多孔介質，對其融化過程進行了數值模擬和試驗研究，旨在研究網狀聚氨酯多孔介質相關參數對延長冰蓄冷板工作時間的影響規律。作為對比，本文還研究了填充高導熱性能泡沫金屬的冰蓄冷板融化過程。

1 數值模擬

冰蓄冷板的物理模型如圖1 所示，模型的左、右兩側面處在對流環境中，其余的上、下、前、后各面均為絕熱，冰蓄冷板中填充開孔泡沫，左、右兩側的環境溫度分別為TL和TR，表面傳熱系數分別為hL和hR。

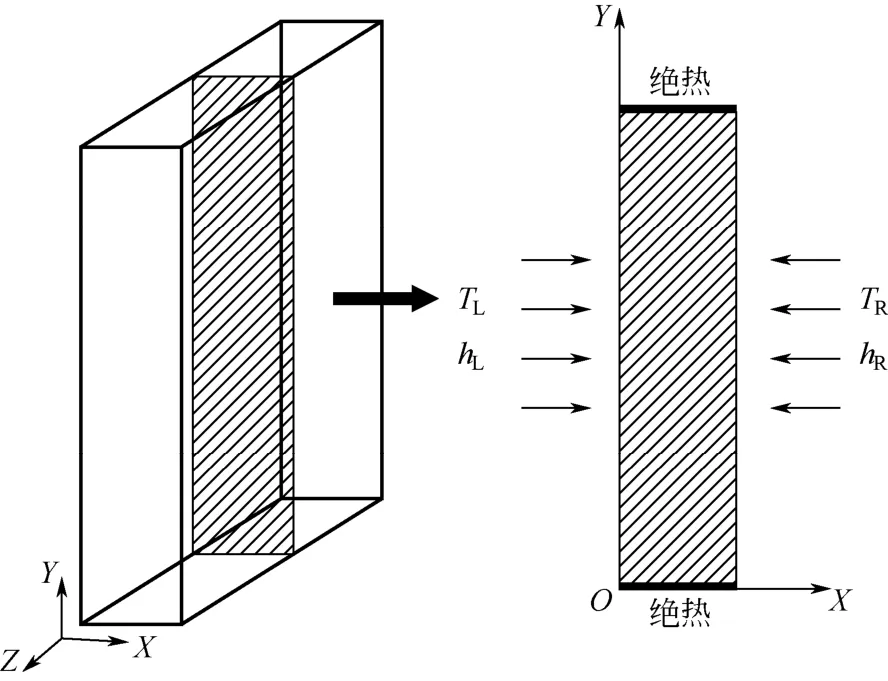
圖1 冰蓄冷板的物理模型

采用Fluent 中的焓-多孔理論模擬融化和凝固問題。該理論將溫度和焓均作為待求函數，建立統一的能量方程，以液相率表示兩相區中的液相體積分數，且假設液相率與溫度呈線性變化關系，通過 不斷更新計算區域內每個單元的液相率來追蹤固液兩相界面的變化[15]。簡化假設如下：①環境空氣為層流，且與固體壁面處于局部熱平衡；②復合相變材料為各向同性，初始溫度均勻；③相變介質的流體為不可壓縮牛頓流體，層流，流體與固體間處于局部熱平衡，忽略黏性耗散，密度服從Boussinesq假設；④相變介質在固、液兩態時為常物性，但在熔融狀態時熱物性參數只隨溫度線性變化。

質量、動量和能量守恒方程[16]分別如式（1）～式（3）。

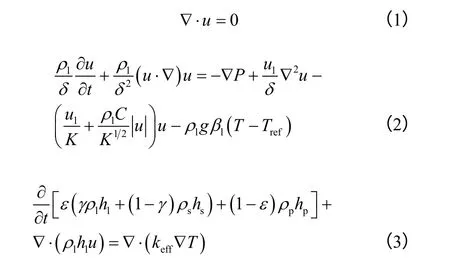
多孔介質的滲透系數K、慣性系數C 和有效熱導率keff采用如式（4）～式（6）的表達式[17]。

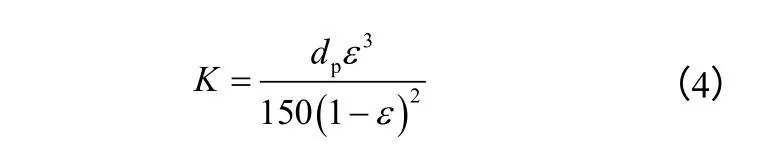
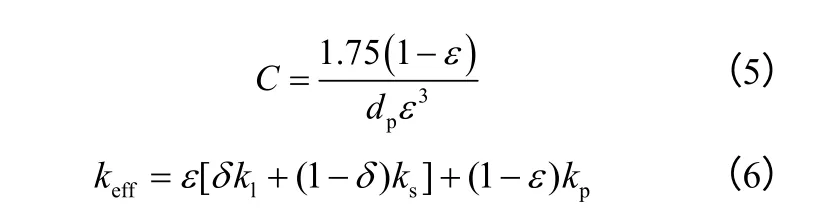
式中，dp為多孔介質的平均孔直徑。

由于在粥狀區，融化具有一定的溫度范圍，液體所占的體積單元分數δ(t)由溫度來確定[18]，如 式（7）。

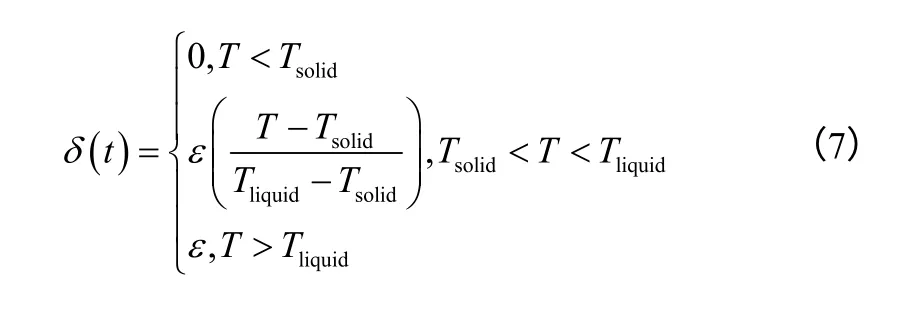
初始條件如式（8）。

邊界條件如式（9）、式（10）。

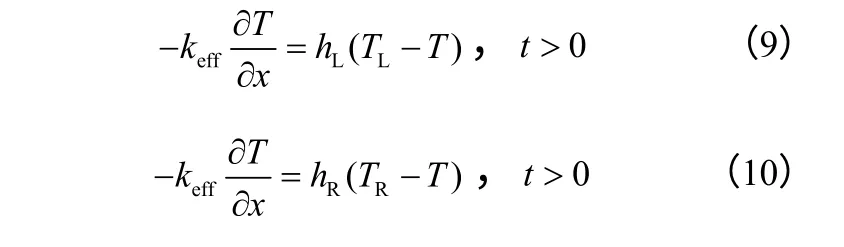
式中，Tinit為初始溫度，K。

使用Gambit 軟件建立模型并采用結構化劃分網格，網格選用四邊形，網格尺寸精度為1mm，冰蓄冷板的計算網格如圖2 所示，其中GZ指向Z 軸的正方向（垂直于紙面向外）。

采用SIMPLE 處理速度和壓力場耦合，固壁邊界。初始溫度設為268K。冰的凝固和液化溫度分別設為271.2K 和273K。融化過程中，從固相區到液相區，冰在孔隙中所占的體積分數由100%線性變化到0。在每個時間步長內對各控制方程進行耦合迭代計算，直至結果收斂。相關的材料熱物性參數如表1[19]所示。

圖2 網格劃分

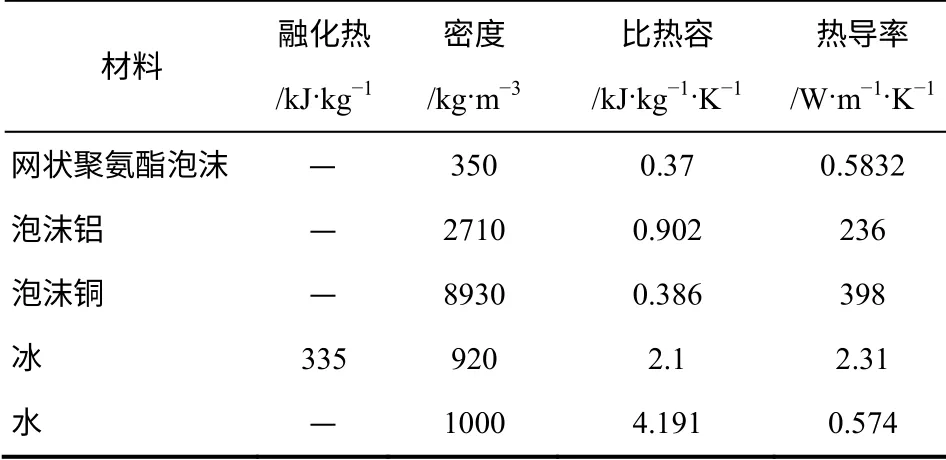
表1 材料熱物性參數

2 模擬結果及分析

2.1 多孔介質的熱導率對溫度分布的影響

圖3 為融化時間約4h 時的冰蓄冷板溫度分布，ω為孔密度，ppi 指每英寸長度的毛孔目數。

由圖3 可見，各冰蓄冷板中相變介質均未完全融化，處于固液共存狀態。橫向上，板內外壁最大溫差，泡沫金屬冰蓄冷板(b)和(c)小于純冰蓄冷板

(a)；縱向上，溫度分布，泡沫金屬冰蓄冷板(b)和(c)比純冰蓄冷板(a)的更均勻，這些說明與純冰蓄冷板相比，泡沫金屬冰蓄冷板的溫度分布更佳。這可能是由于金屬的高導熱性能所致。金屬的導熱遠遠大于純冰，添加泡沫銅或泡沫鋁后，冰蓄冷板整體熱擴散能力得到很大提升，冰蓄冷板外壁的熱量能夠迅速地傳向內部，不僅不會出現“熱堆積”現象，而且由于金屬骨架的作用，熱量能夠更好地分散到蓄冷板的各部分。并且，泡沫銅冰蓄冷板(c)的溫度分布略優于泡沫鋁冰蓄冷板(b)，這是由于銅的熱導率高于鋁所致。

圖3(d)是網狀聚氨酯泡沫冰蓄冷板的溫度分布，比較網狀聚氨酯泡沫冰蓄冷板(d)和純冰蓄冷板(a)發現，不論縱向上和還是橫向上，兩者溫差接近，前者稍高于后者。出現這一結果，可能是聚氨酯泡沫的熱導率小于純冰（近似為純冰的1/4），網狀聚氨酯泡沫冰蓄冷板的整體冰蓄冷板的導熱能力小于純冰蓄冷板，熱擴散能力減小，使得傳熱速率減小；此外，在一定程度上，網狀聚氨酯泡沫的多孔特性抑制了融化介質的自然對流，阻礙了冰水分層，降低了不同溫度區域的交互作用。

2.2 多孔介質的熱導率對相界面的影響

圖4 為融化時間約4h 時冰蓄冷板的相界面情況。

由圖4 可見，融化相同時間后，純冰蓄冷板(a)內部出現了明顯的固液相界面輪廓，下端出現半橢圓弧狀相界面，圓弧上方為尚未融化的固態介質，下方紅色區域為已融化的液態介質，兩區域間為固

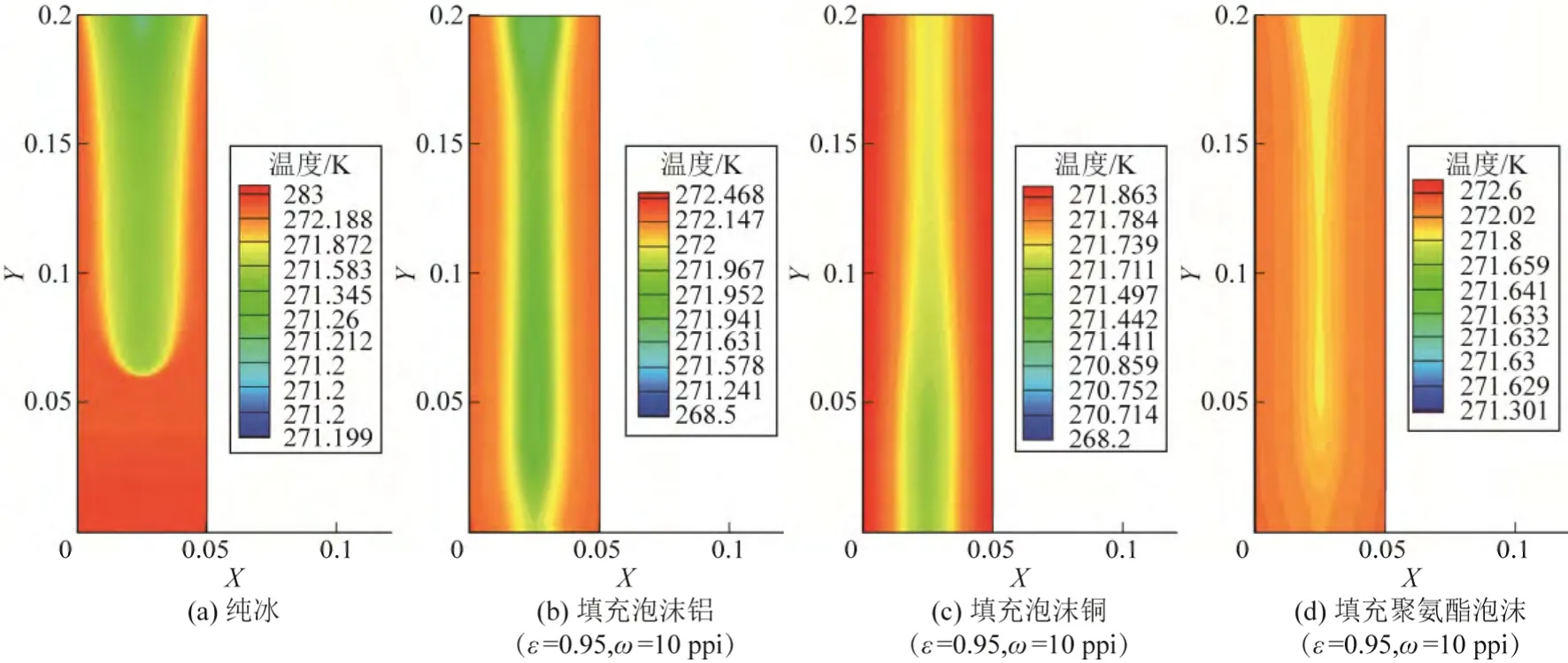
圖3 冰蓄冷板溫度分布

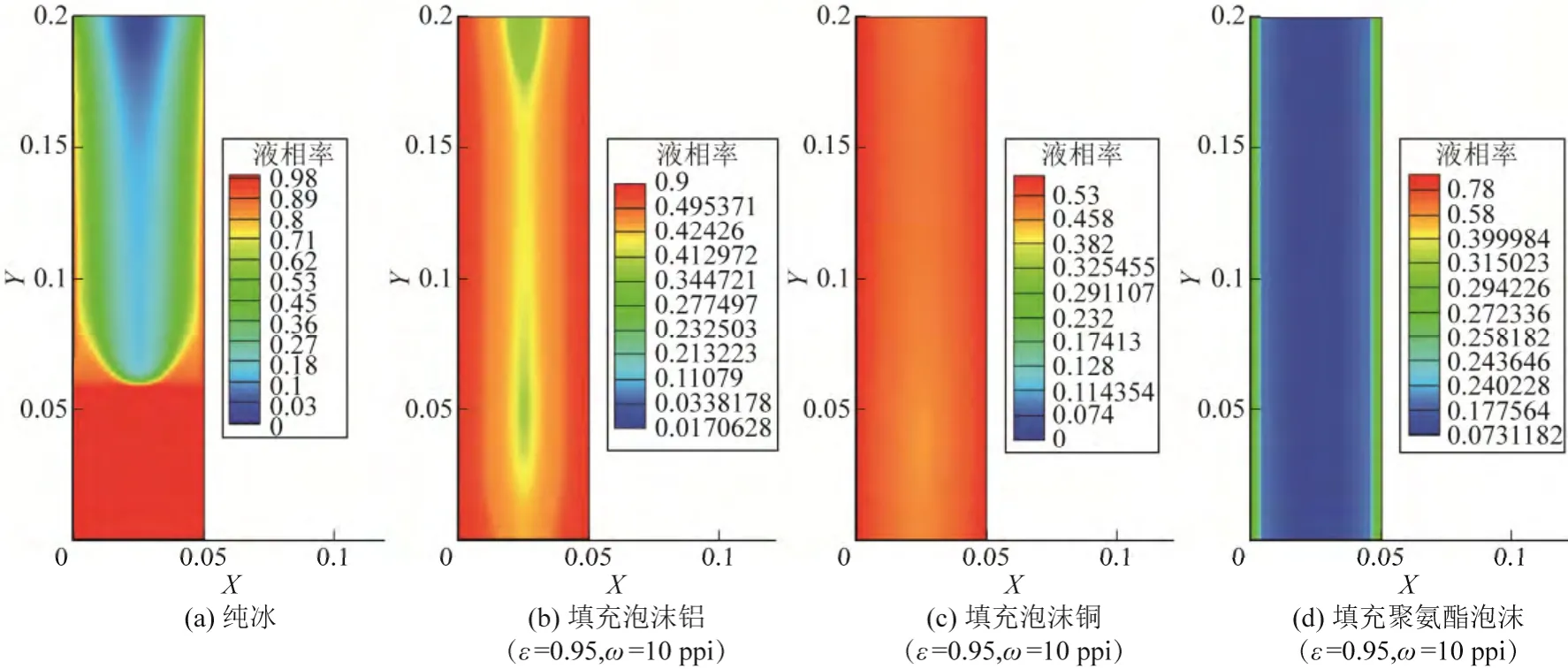
圖4 冰蓄冷板相界面

液共存的糊狀區；相比較之下，泡沫金屬冰蓄冷板(b)和(c)內部的固液相界面形狀較模糊。出現這一情況的原因可能是：①泡沫金屬冰蓄冷板的整體導熱性能高于純冰蓄冷板，熱擴散性好，溫度分布均勻，融化過程在更大的區域進行，不會出現純冰時“上液下固” 明顯的相界面分層；②泡沫金屬的多孔性可能抑制了冰水混合物中的自然對流，從而下段未出現由于固液密度差引起的半橢圓弧狀相界面；③還可能是泡沫金屬冰蓄冷板的融化速率快，已融化相變介質的液相率較高，弱化了固液區域分層。對比網狀聚氨酯泡沫冰蓄冷板(d)和純冰蓄冷板(a)可見，網狀聚氨酯泡沫冰蓄冷板內的液態區面積小于純冰的，這表明網聚氨酯泡沫的低導熱性能減小了冰的融化速率，延長了冰蓄冷板的工作時間。此外，聚氨酯泡沫冰蓄冷板內固液相界面分布要比純冰的更加模糊，這可能同樣是由于聚氨酯泡沫的多孔特性抑制了固液的自然對流所致，導致滲透性減小，滲透系數下降，降低了融化速率。

2.3 多孔介質的熱導率對融化時間的影響

圖5 是填充相同孔隙參數的不同多孔介質時冰蓄冷板內的液相率隨時間的變化。

由圖5 可見，添加多孔介質后，冰蓄冷板的融化時間隨填充材料導熱能力的增加而減小。這是由于添加高導熱能力的泡沫銅或泡沫鋁時，可以有效提高復合相變材料的熱導率，從而加快融化速率，縮短融化時間。銅的熱導率高于鋁，所以添加泡沫銅后，融化時間更短。相反，添加低導熱能力的網狀聚氨酯降低了復合相變材料的熱導率，使融化速率減小，融化時間延長。

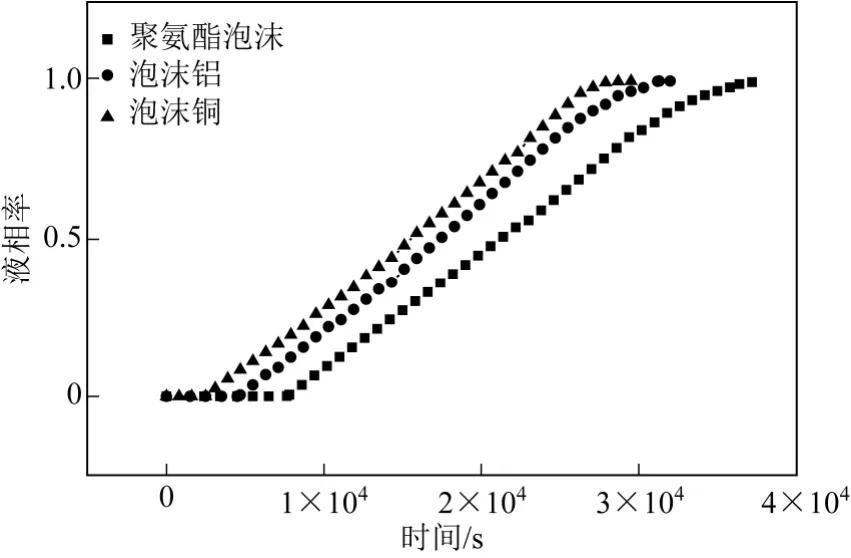
圖5 熱導率對液相率的影響

2.4 多孔介質的孔隙率對融化時間的影響

圖6 是多孔介質的不同孔隙率（孔密度為10ppi）條件下冰蓄冷板內的液相率隨時間的變化。

由圖6(a)和(b)可見，填充泡沫金屬時，冰蓄冷板的冰融化時間隨孔隙率的增加而延長，泡沫銅冰蓄冷板的融化時間受孔密度變化的影響大于泡沫鋁冰蓄冷板的；由圖6(c)可見，當填充網狀聚氨酯泡沫時，融化時間隨孔隙率的減小而縮短。原因可能如下：①熱導率的影響，填充泡沫金屬使得冰蓄冷板導熱能力增大，且孔隙率越小，導熱能力越大，融化時間越短；填充網狀聚氨酯泡沫使得冰蓄冷板導熱能力減小，且孔隙率越小，導熱能力越小，使得融化時間越長；②相變介質的質量比例影響，隨著孔隙率的減小，冰的質量分數會有所減少，這可能也導致相變介質融化時間縮短。

2.5 多孔介質的孔密度對融化時間的影響

圖7 分別為填充泡沫鋁、泡沫銅、網狀聚氨酯泡沫的不同孔密度（孔隙率為0.95）時，融化過程中液相率隨時間變化的影響。由圖7(a)和圖7(b)可見，孔隙率一定時，泡沫金屬的孔密度對融化過程的影響較小。表明對于高熱導率材料，高孔密度對自然對流的削弱作用大于增加表面積對換熱的強化作用。由圖7(c)可見，孔隙率一定時，網狀聚氨酯泡沫的孔密度對融化過程的影響較大。隨著孔密度增大，融化時間延長，表明對于低熱導率材料，高孔密度對自然對流的較大的削弱作用抑制了熱量的傳遞。對比圖6 和圖7 發現，泡沫金屬孔隙率對融化速率的影響作用大于孔密度。

3 試驗結果及討論

分別對填充泡沫銅和網狀聚氨酯泡沫復合相變材料的冰蓄冷板進行了融化時間的測定。試驗用到 的多孔介質表征參數見表2。

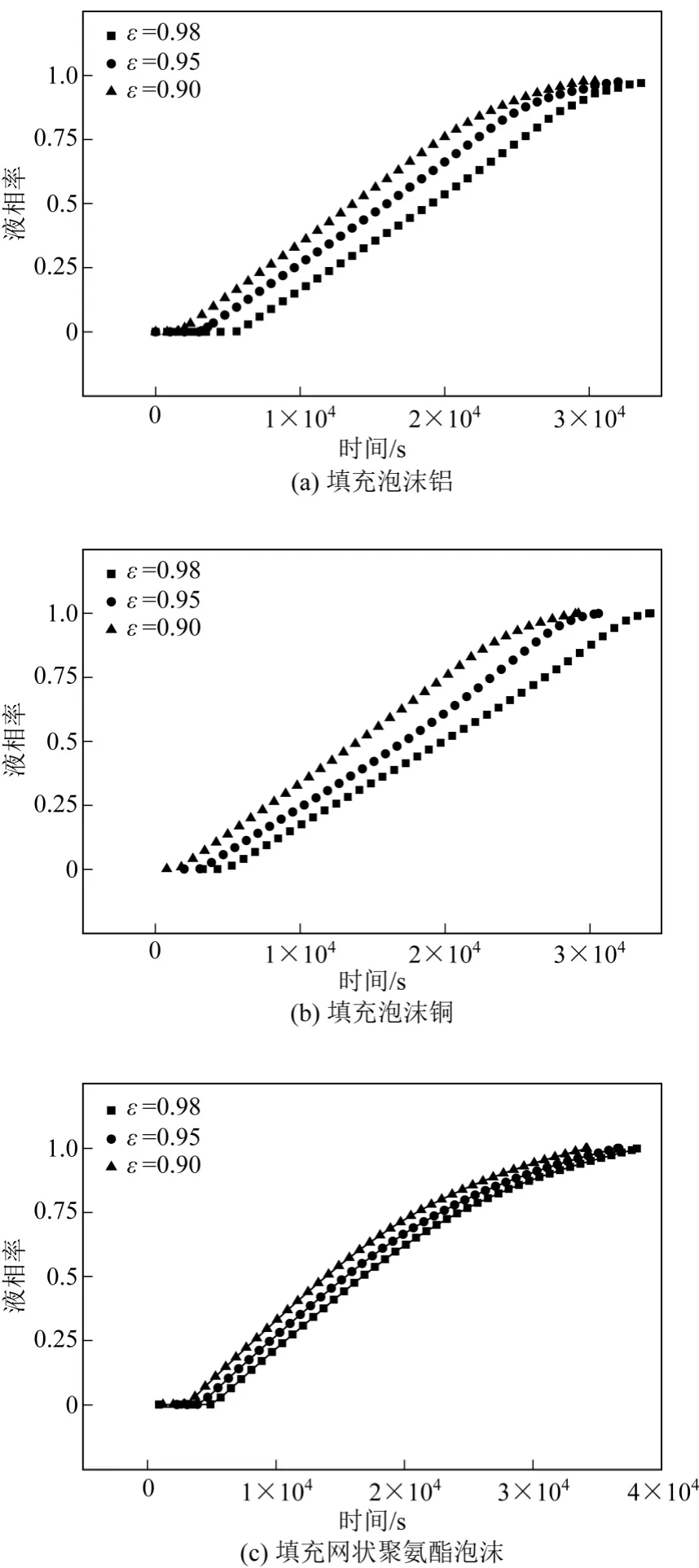
圖6 孔隙率對液相率的影響

冰蓄冷板的尺寸均為：長×寬×高=20cm×10cm×5cm。試驗條件設定如下：TL=TR=293K，hL=hR=8W/(m2·K)。冰蓄冷板初始溫度均為268K。根據測量冰層厚度隨時間的變化，可計算出液相率隨時間的變化；同時將融化產生的液態水收集，也可以測算出液相率。試驗過程的液相率結果取這兩種不同方法的算術平均值。試驗臺示意如圖8。

3.1 多孔介質的熱導率對冰蓄冷板融化過程的 影響

圖9 是填充孔隙率均為0.95、孔密度均為10ppi的泡沫銅和網狀聚氨酯泡沫的冰蓄冷板釋冷過程中的液相率隨時間變化的測定結果。

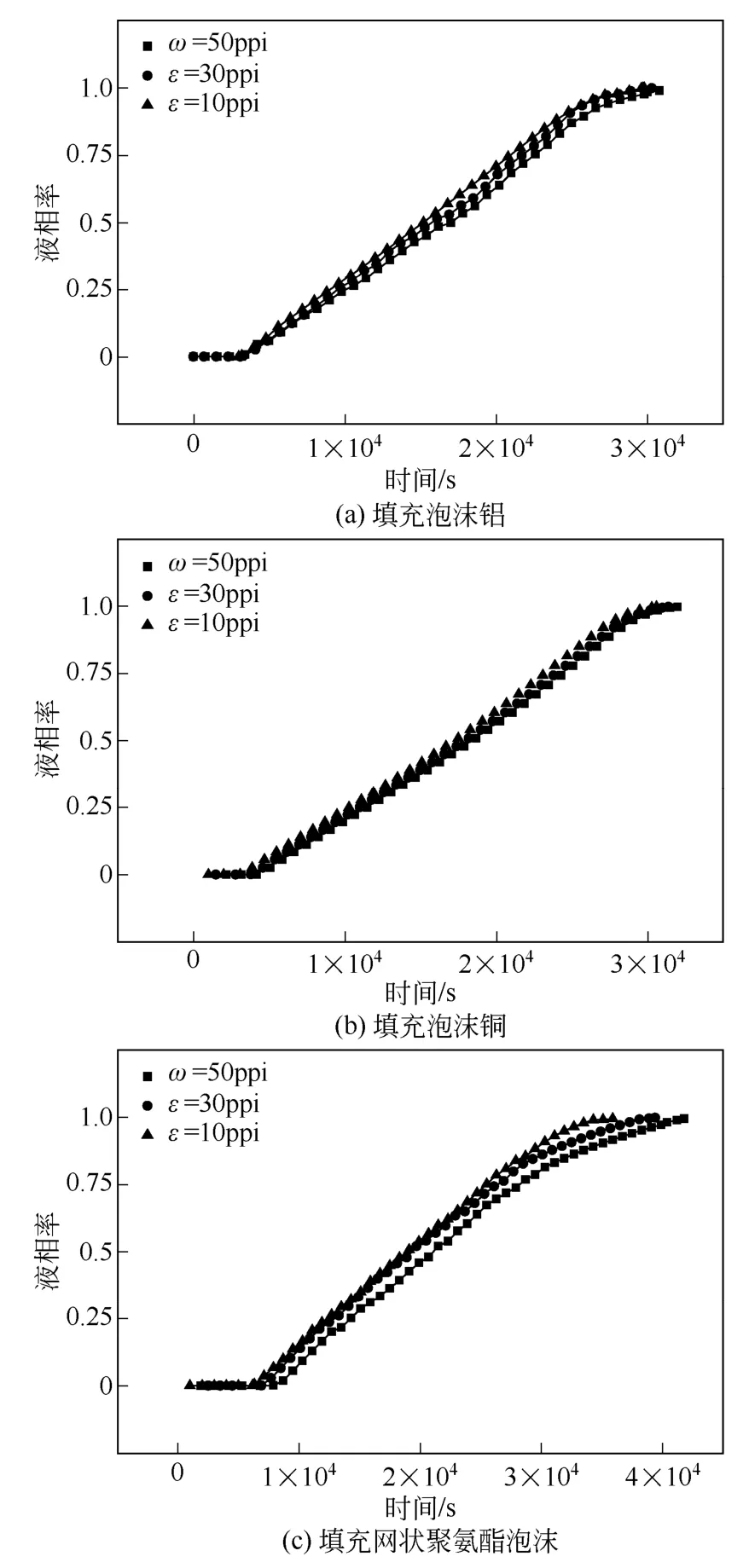
圖7 孔密度對液相率的影響

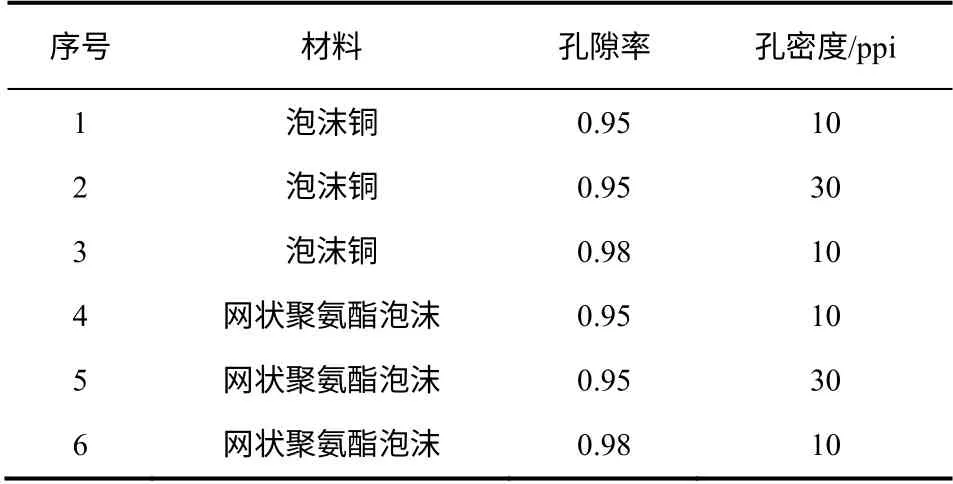
表2 試驗用多孔介質表征參數

由圖9 可見，初始時刻各冰蓄冷板的液相率均為0，這表明由于初始時刻各冰蓄冷板的溫度遠低

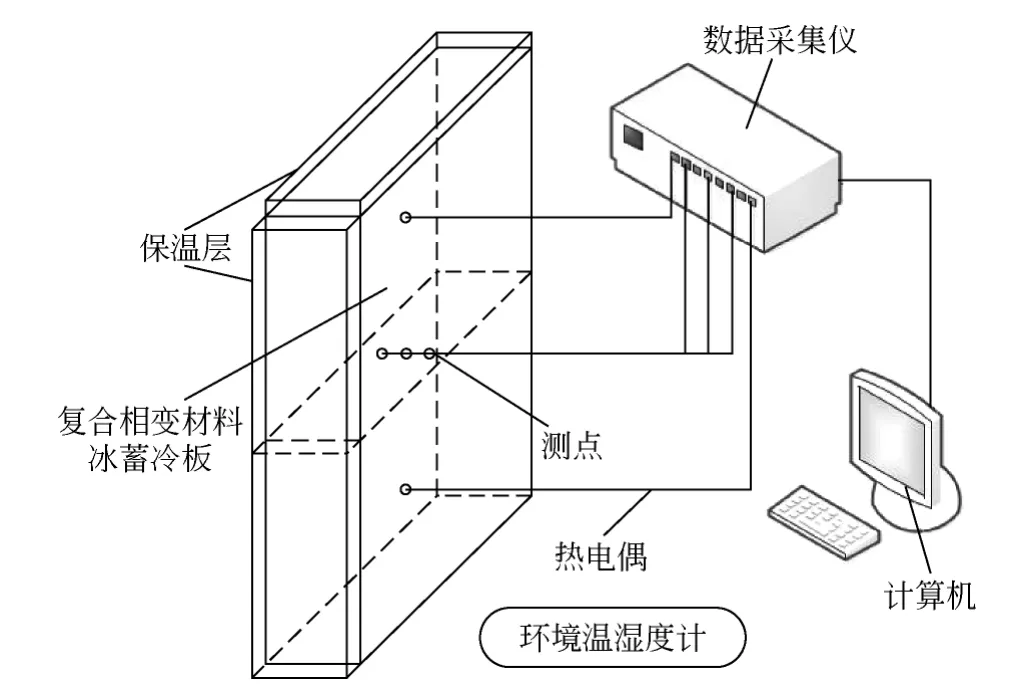
圖8 試驗臺示意圖

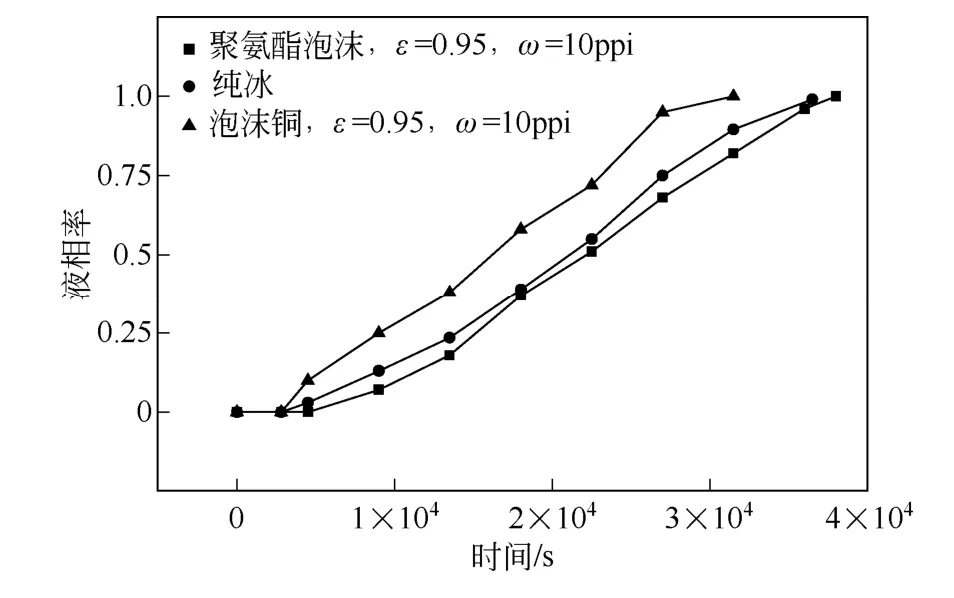
圖9 不同熱導率多孔介質下液相率隨時間變化的 曲線

于其相變溫度，此時與環境間屬于顯熱交換，尚未發生相變，因而無液體水產生。當經歷一時間段后，填充泡沫銅的冰蓄冷板液相率首先開始出現變化，這表明其先于填充網狀聚氨酯泡沫的冰蓄冷板到達相變溫度。此后，兩者的液相率均隨時間延遲而提高，并且在相同時刻，填充泡沫銅冰蓄冷板的液相率均高于填充聚氨酯泡沫。最終，填充泡沫銅冰蓄冷板的液相率先達到100%，這表明其已經完全融化。填充泡沫銅冰蓄冷板的融化時間比填充網狀聚氨酯泡沫縮短21%。這是由于銅的熱導率遠大于網狀聚氨酯泡沫，使得泡沫銅冰蓄冷板的總體換熱效果要優于聚氨酯泡沫冰蓄冷板的，故前者融化速率要高于后者。

3.2 多孔介質的孔密度對冰蓄冷板融化過程的 影響

圖10 是純冰與填充孔隙率均為0.95、不同孔密度的泡沫銅和網狀聚氨酯泡沫冰蓄冷板釋冷過程中的液相率隨時間變化的測定結果。

由圖10(a)可見，10ppi 的網狀聚氨酯泡沫冰蓄冷板的融化速率快于30ppi 的。與純冰相比，10ppi的網狀聚氨酯泡沫冰蓄冷板可將釋冷時間延長9.8%，ω=30ppi 的可延長14.3%。表明孔密度對融化過程產生了影響，說明低孔密度對冰融化過程中冰水間的自然對流具有較小的抑制作用，驗證了模擬分析結果。對比圖7 和圖10，曲線的整體趨勢較為一致，具有較高的吻合度，也證明了模型的可 靠性。

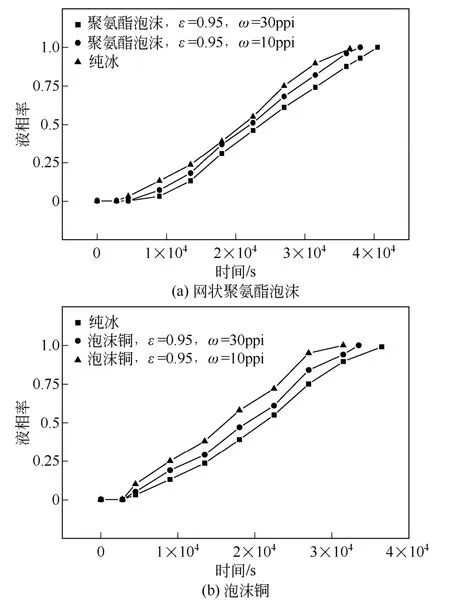
圖10 不同孔密度下液相率隨時間變化的曲線

由圖10(b)可見，10ppi 的泡沫銅冰蓄冷板的融化速率快于30ppi 的。與純冰相比，10ppi 的泡沫銅冰蓄冷板可將相變時間縮短15.2%，30ppi 的縮短11.4%。這表明高熱導率的多孔介質其孔密度對融化過程的影響較大。孔密度較低時，平均孔徑相對較大，孔隙對自然對流的抑制作用較小，對于融化過程中的熱交換有利，可提高融化速率。

3.3 多孔介質的孔隙率對冰蓄冷板融化過程的影響

圖11 為純冰與填充孔密度均為10ppi、不同孔隙率的泡沫銅和網狀聚氨酯泡沫冰蓄冷板釋冷過程中的液相率隨時間變化的測定結果。

由圖11(a)中可見，ε=0.95 的網狀聚氨酯泡沫冰蓄冷板的液相率和ε=0.98 的差別很小，兩者的融化速率基本一致。與純冰相比，前者可將釋冷時間延長9.8%，后者延長11.8%。這表明，對于低熱導率 的多孔介質，孔隙率對融化速率影響較小，遠小于孔密度的影響，這和模擬結果較為一致。

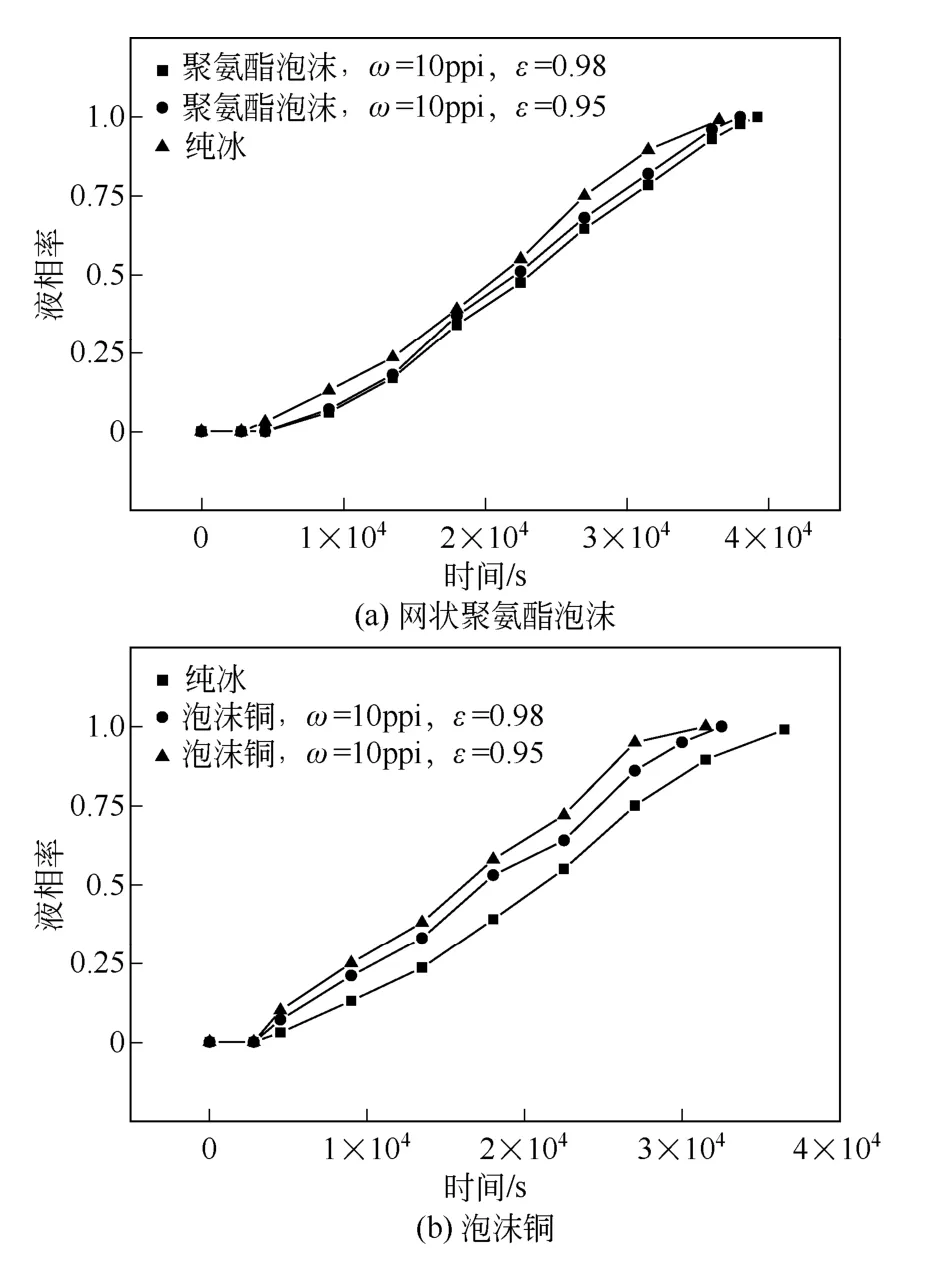
圖11 不同孔隙率下液相率隨時間變化的曲線

由圖11(b)中可見，ε=0.95 的泡沫銅冰蓄冷板的融化速率明顯快于ε=0.98 的。與純冰相比，前者可以將融化時間縮短15.2%，后者可縮短8.1%。這是由于孔隙率相對較低時，多孔介質在復合相變材料中所占體積較大，高熱導率的多孔介質會使得冰蓄冷板的整體導熱性能提高，因而加快了融化速率。這也表明，對于高熱導率多孔介質，孔隙率對融化速率影響較大，大于孔密度的影響，這和理論模擬結果的趨勢也較為一致，具有較高的吻合度。

4 結 論

本文通過對填充多孔介質冰蓄冷板融化過程進行模擬和試驗研究，對比了不同表征參數的多孔介質對冰蓄冷板融化過程的影響。結果顯示：多孔介質的熱導率會對冰蓄冷板融化速率產生較大影響。與純冰相比，本研究中熱導率較高的泡沫鋁、泡沫銅等可以將冰蓄冷板融化時間縮短最多達15.2%，冰蓄冷板的融化速率會隨孔隙率或孔密度的減小而增加，孔隙率變化對融化速率的影響更大。熱導率較低的網狀聚氨酯泡沫可以將冰蓄冷板釋冷時間延長最多達11.8%，冰蓄冷板的釋冷時間隨孔隙率或孔密度的增大而增加，孔密度變化對釋冷時間的影響更大。

符 號 說 明

C—— 慣性系數，m-1

Cp—— 比熱容，J·kg-1·K-1

dp—— 多孔介質的平均直徑，m

h—— 對流換熱系數，W·m-2·K-1

K—— 滲透系數，m2

k—— 熱導率，W·m-1·K-1

L—— 融解熱，J·kg-1

T—— 溫度，K

V—— 體積，m3

ε—— 孔隙率

γ—— 液體所占孔隙分數

δ—— 液體所占體積單元分數

ρ—— 密度，kg·m-3

ω—— 孔密度，ppi（單位英寸孔目數）

下角標

eff—— 有效的

init—— 初始時刻

L—— 冰蓄冷板左側

l—— 液態相變介質

liquid—— 融化

p—— 多孔介質

pcm—— 相變介質

R—— 冰蓄冷板右側

s—— 固態相變介質

solid—— 凝固

[1] Zalba B，Marín J M，Cabeza L F，et al. Review on thermal energy storage with phase change：Materials heat transfer analysis and applications[J]. Applied Thermal Engineering，2003，23：251-283.

[2] 馬素德，宋國林，樊鵬飛，等. 相變儲能材料的應用及研究進展[J]. 高分子材料科學與工程，2010，26（8）：161-164.

[3] 于欣，胡曉峰，黃占華. 有機/復合相變儲能材料研究進展[J]. 功能材料，2012，43（B08）：16-21.

[4] Rozanna D，Chuanh T G，Salmiah A，et al. Fatty acids as phase change materials（PCMs） for thermal energy storage：A review[J]. International Journal of Green Energy，2005，1（4）：495-513.

[5] 汪雙鳳，李炅，張偉寶. 開孔泡沫金屬用于緊湊型熱交換器的研究進展[J]. 化工進展，2008，27（5）：675-678.

[6] 張龍龍，龔峻松，宋光濤，等. 泡沫金屬填料旋轉床用于CO2的吸收[J]. 化工進展，2012，31（10）：2157-2161.

[7] Jegadheeswaran S，Pohekar S D. Performance enhancement in latent heat thermal storage system：A review[J]. Renewable and Sustainable Energy Reviews，2009，13（9）：2225-2244.

[8] Mesalhy O，Lafdi K，Elgafy A，et al. Numerical study for enhancing the thermal conductivity of phase change material（PCM） storage using high thermal conductivity porous matrix[J]. Energy Conversion and Management，2005，46（6）：847-867.

[9] Martin V，He B，Setterwall F. Direct contact PCM-water cold storage[J]. Applied Energy，2010，87（8）：2652-2659.

[10] Siahpush A，O’Brien J，C’repeau J. Phase change heat transfer enhancement using copper porous Loam[J]. Journal Heat Transfer，2008，130：1-11.

[11] 吳志根，趙長穎，顧清之. 多孔介質在高溫相變蓄熱中的強化換熱[J]. 化工學報，2012，63（s1）：119-122.

[12] 王杰利，屈治國，李文強，等. 封裝有相變材料的金屬泡沫復合散熱器實驗研究[J]. 工程熱物理學報，2011，32（2）：295-298.

[13] 楊秀，陳振乾. 蓄冰球中填充泡沫鋁的融化相變傳熱過程的數值模擬[J]. 化工學報，2008，59（s2）：139-142.

[14] Shiina Y，Inagaki T. Study on the efficiency of effective thermal conductivities on melting characteristics of latent heat storage capsules[J]. International Journal of Heat and Mass transfer，2005，48（2）：373-383.

[15] ANSYS Inc. ASNSY FLUENT12.0 Theory Guide[M]. USA：ANSYS Inc.，2009

[16] 盧濤，姜培學. 多孔介質融化相變自然對流數值模擬[J]. 工程熱物理學報，2005，26（6）：167-170.

[17] 林瑞泰. 多孔介質傳熱傳質引論[M]. 北京：科學出版社，1995：111-128.

[18] 郭寬良，孔祥謙，陳善年. 計算傳熱學[M]. 合肥：中國科學技術大學出版社，1988：68-69.

[19] 闞安康，韓厚德，湯偉. 基于分形理論的開孔聚氨酯泡沫等效熱導率研究[J]. 材料導報，2012，26（2）：143-146.