由地震危險性分析估計場地地震動持續時間

錢向東 崔賽飛 程玉瑤

（河海大學 力學與材料學院，南京 210098）

持續時間是描述地震地面運動特性的3大要素之一［1－2］，對工程結構的非線性地震反應，特別是累積破壞具有顯著的影響［3－10］.然而，由于目前的地震動區劃中并沒有給出場地的地震動持續時間［11］，采用動力時程法分析結構地震反應時，對持續時間的選取存在較大的主觀隨意性，因此，在實際的地震工程中，持續時間并沒有像振幅和頻譜那樣得到充分的考慮.

類似于其它地震動參數的估計，根據衰減關系建立經驗型預測方程，是目前估計和預測場地地震動持續時間的可行方法，文獻［12］對持時的各類定義和最新的持時預測方程進行了介紹和評價.由于地震的不確定性，估計和預測場地地震動持續時間時應該充分考慮各潛在震源的影響.申愛國［13］、汪夢甫［14］、高玉峰等［15］將地震危險性分析引入持時的估計與預測，針對選取的場地，采用麥圭爾（McGuire R K）［16］持時預測方程，給出了相應的場地地震動持續時間.

本文根據地震危險性概率分析方法，采用能量持時定義和 Bommer－tafford－Alarcón預測 方程［17］，以某城市商務區為例，計算了不同設防水準下場地的地震動持續時間.

1 地震危險性概率分析方法

地震危險性分析方法主要有確定性方法和不確定性方法（常稱為概率法）兩種.由于地震本身就存在不確定性，因此，概率法是目前地震危險性分析中應用最廣泛的方法.地震危險性概率分析方法考慮所有可能發生地震的地區和發生各個震級地震的可能性，綜合地震活動在時間、空間和強度方面的統計特征，建立數學模型，將地震地質條件與地震活動性資料結合起來，確定影響場地地震安全性的潛在震源區、地震活動性參數以及地震動衰減關系，最終估計給定地點地震動超過某一閾值的可能性，并用超越概率的方式表達［18－19］.

1.1 基本假定

1968年Cornell［20］采用超越概率和平均重現期的表達方式，對模型的建立提出了以下幾個基本假定：

1）地震活動在空間上不是完全隨機分布的，它只分布在劃定的潛在震源區內，并且在潛在震源區內地震發生的可能性處處相同.而潛在震源區是綜合歷史地震、大地構造和地質條件確定的；

2）在每個潛在震源區內，地震事件彼此獨立，地震發生的時間過程符合泊松模型，即在時間段t內發生n次地震的概率為

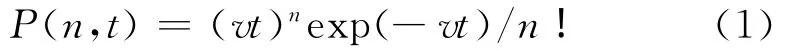
式中，v是地震的平均年發生率.

3）在一個潛在震源區內地震事件的震級分布為指數分布，震級大于M的次數N（M）與震級的關系滿足古登堡－里克特震級－頻度關系；

4）場地地震動參數是震中距（或震源距）和震級的函數.

1.2 場地地震動超越概率及其計算公式

針對某一場地，存在N個有影響的潛在震源區，則根據基本假定和全概率公式，可得到場地一年中地震動Y超過某確定值y的概率（年超越概率）為［18－19］

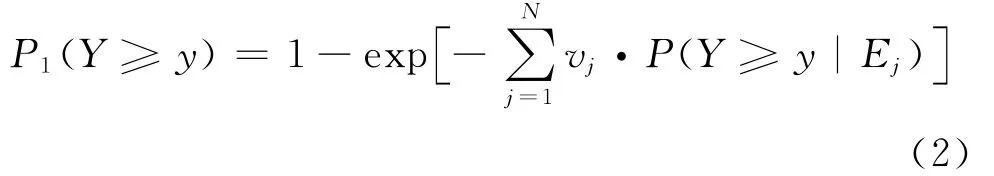
其中，vj為第j個潛在震源區地震的年平均發生率；P（Y≥y｜Ej）為第j個潛在震源區發生地震時的超越概率，由該潛在震源區發生各震級M的地震的貢獻P（Y≥y｜Ej，M）疊加而成.

同時假定場地每年發生地震動的最大強度互不影響且各年的年超越概率保持為常數不變，根據伯努利重復試驗的公式可得T年內相應的超越概率為

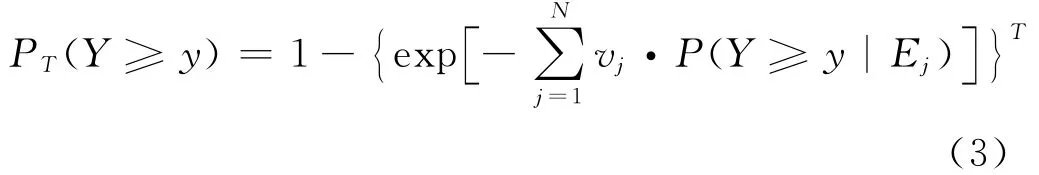
考慮震源斷裂的方向性效應，假設潛在震源區內構造走向與正東方向的夾角為θ，分別對各θ方向求出該潛在震源的貢獻P（Y≥y｜Ej｜θi），然后與θ方向的取向概率相乘疊加得：

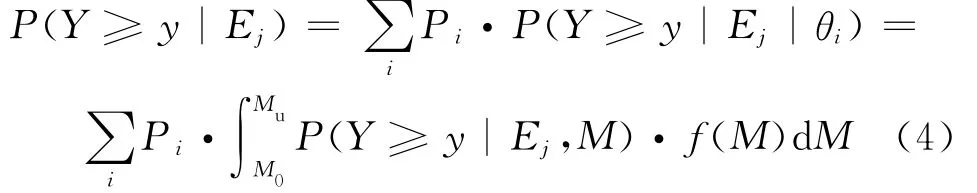
式中，Pi為相應的取向概率，根據斷層類型按以下3種情況進行取值［21］：

1）單一斷層性質：沿斷層方向取向概率為1；

2）共軛斷層性質：沿兩組交匯的共軛斷層方向取向概率各取50%.

3）一組斷層為主，另一組斷層為輔：沿主斷層方向的取向概率值為70%，沿次要斷層方向的取向概率為30%.

所以場地T年內的超越概率為

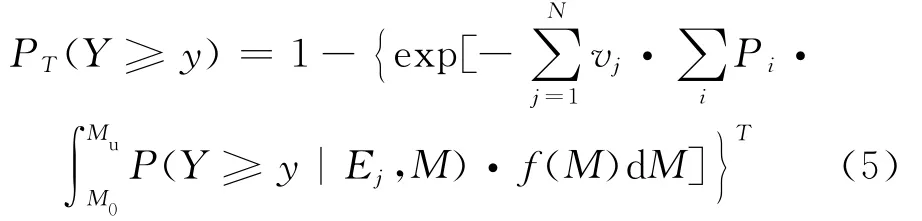
其中f（M）為震級M的概率密度函數：

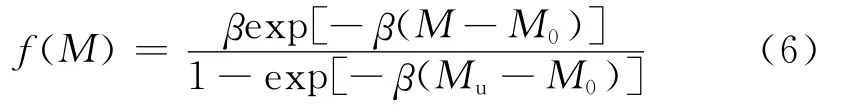
式中，β＝b×ln10，Mu為地震帶的震級上限；M0是指可以對場地造成破壞的最小震級，通常取M0為4.0級.

2 持時預測模型

場地發生地震動必然是由周圍的潛在震源發生地震而引起，發生一次地震動就會在場地對應有一個地震動持續時間，因此預測未來一場地發生地震的持續時間可以表示為各潛在震源區發生地震的持續時間對場地的概率貢獻之和.假設有N個潛在震源區發生地震時對場地的地震動強度有影響，且有影響的各潛在震源區概率貢獻為Pj，根據持時預報方程，由各潛在震源區計算得到的場地地震動的最大持時為Tj，則場地未來發生地震的地震動持續時間T可以表示為［15］：

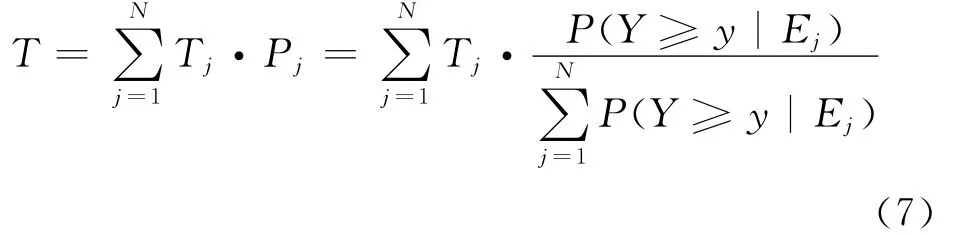
其中，Tj可根據持續時間的預測方程求得.

應用最廣泛的持時預測方程為麥圭爾（McGuire R K）1979年提出的90%能量持時預測方程［16］：

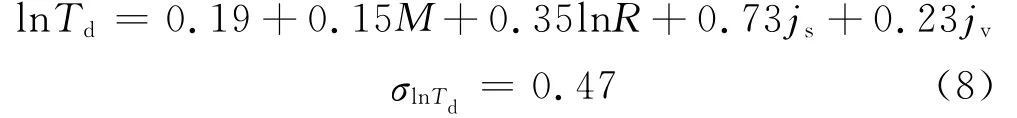
式中，js為場地因子，基巖js＝0，中等土js＝1，沖擊土js＝2；jv為分量因子，水平向地震動jv＝0，豎向jv＝1.

目前，考慮影響因素最全面的持時預測方程為Bommer－Stafford－Alarcón模型，其90%能量持時預測方程為［17］：

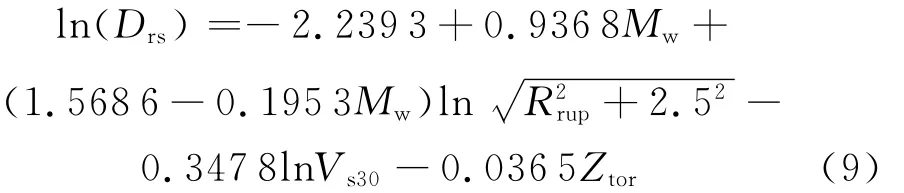
式中，Drs為相對能量持時；Mw為矩震級；Rrup為場地至震源的最短距離（km）；Vs30為場地表面以下30m土層中剪切波的平均速度（m／s）；Ztor為破裂面頂部深度（km）.

3 應用算例

為了驗證計算模型與方法的正確性，與文獻［13］一樣，采用麥圭爾（McGuire R K）90%能量持時預測方程［16］計算了嘉峪關市50年不同超越概率水準下地震動持續時間，計算結果見表1.兩者非常接近.

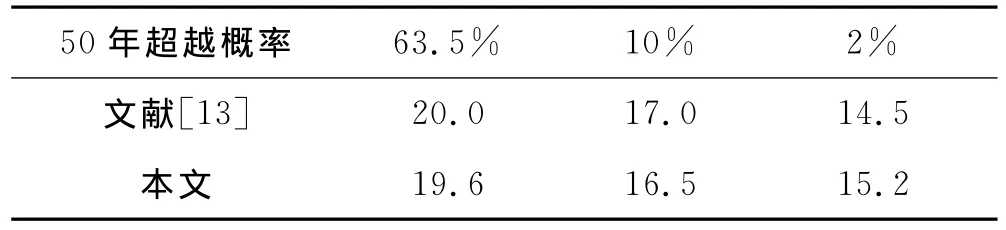
表1 嘉峪關市地震動持續時間 （單位：s）

本文以某濱江城市為例，根據地震區劃工作成果，其商務區的潛在震源主要分步在兩大地震帶：長江下游－南黃海地震帶和郯廬地震帶.根據潛在震源區的劃分原則以及區劃圖綜合劃分方案，工程場地所在區域范圍內在“中國地震動參數區劃圖（2001）”［11］上共劃分出32個潛在震源區，如圖1所示.

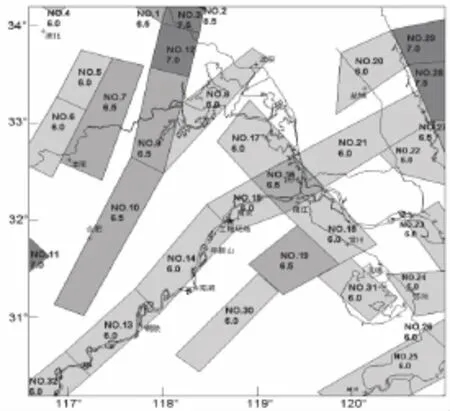
圖1 潛在震源區劃分圖

該地區的基巖地震動峰值加速度衰減關系選用汪素云提出的中國東部地區基巖地震動水平向峰值加速度衰減關系［22］，即

長軸：

短軸：

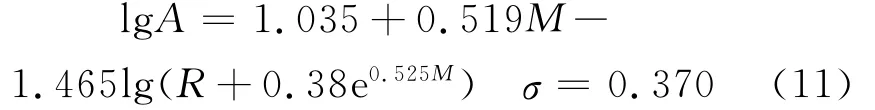
式中，A為峰值加速度，M為震級，R為震中距，σ為衰減關系的標準差.

經過分析，在32個潛在震源區中對工程場地影響較大的有：臨沭潛在震源區（No.2）、南京潛在震源區（No.15）、馬鞍山潛在震源區（No.14）、揚州潛在震源區（No.16）和溧陽潛在震源區（No.19）.因此在計算時主要考慮這5個潛在震源區.由圖1可以看出：南京潛在震源區和馬鞍山潛在震源區的主破裂方向為與正東方向夾角45°，這是一種單一斷層走向類型，因此取向概率為1.臨沭潛在震源區的主破裂方向為與正東方向夾角60°，也是一種單一斷層走向類型，取向概率為1.揚州和溧陽潛在震源區存在共軛斷層，地震破裂面沿共軛斷層走向產生，兩個方向分別為與正東方向夾角45°和135°，概率各占50%.由式（4）和式（5）可以求出不同年超越概率水平下各潛在震源區的概率貢獻Pj，結果見表2.

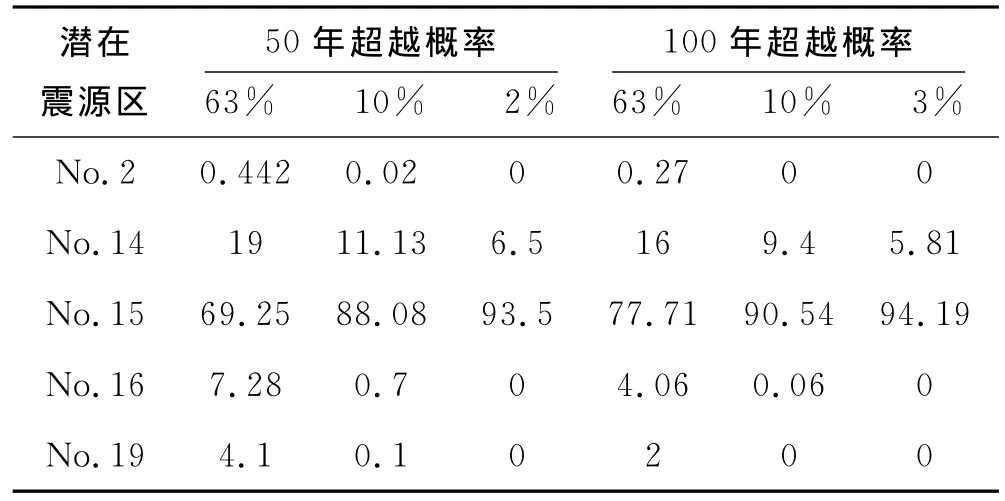
表2 不同年超越概率水平下各潛在震源區的概率貢獻Pj（%）

由式（7）和持時預測方程（8）、（9）即可求出某市商務區不同超越概率水準下地震動持續時間，計算結果見表3.

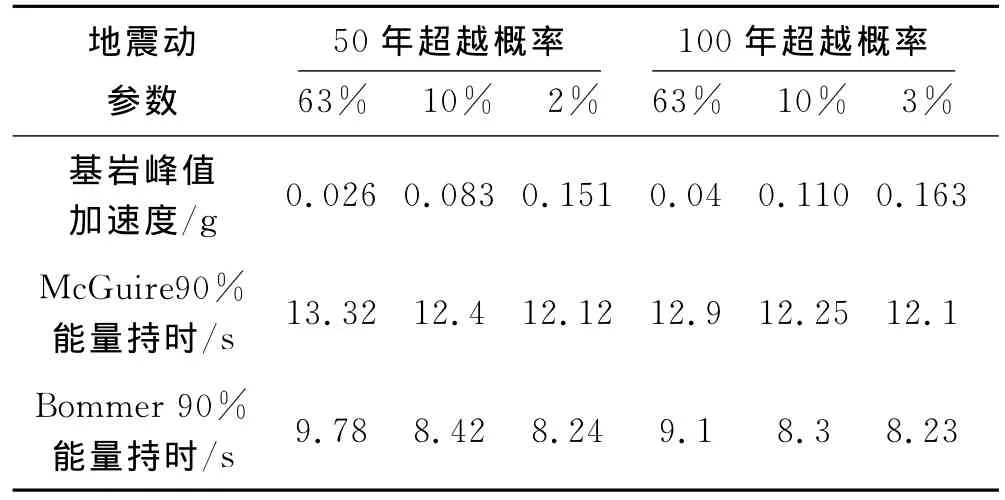
表3 某市商務區地震動持時預測結果

計算結果表明：隨著設防水準降低，地震動持續時間增大.對于超越概率63%設防水準下，對場地有貢獻的潛在震源區數目多分布范圍廣，遠震、近震、大震、小震都對場地有影響，且震級上限值較大，所以地震動持續時間較長；而超越概率10%和2%的設防水準下，近場潛在震源區的影響較大，且有貢獻的潛在震源區數目減少，當超越概率為2%時，有貢獻的潛在震源僅有N0.14和NO.15兩個，相對而言地震動持續時間較短.

該方法以各潛在震源發生地震在場地產生的最大持時與概率貢獻的乘積之和作為場地地震動持時的預測值，該值作為一個期望值可能會小于實際發生地震的持續時間，然而取各潛在源場地產生的最大持時進行計算可以彌補這一誤差，得到比較合理的結果.

4 結 論

基于地震危險性概率分析方法的持時預測繼承了地震危險性分析的概率思想，將地震動持續時間作為隨機變量來考慮，實現了地震動強度和持續時間二者在同一概率意義下的協調和統一，適應了目前結構設計的可靠度理論發展需要，預測出的持續時間與場地的設防水準相對應，具有十分重要的工程實際意義.

本文給出了某市商務區不同超越概率水平下的地震動參數和地震動持時預測結果，可作為本地區工程抗震設計與防震減災工作的參考依據.

［1］ 胡聿賢.地震工程學［M］.北京：地震出版社，2006.

［2］ Douglas J.Earthquake Ground Motion e 41（Stimation Using Strongmotionrecords：A Review of Equations for the Estimation of Peakground Accelerations and Response Spectral Ordinates，Earth－ScienceRev，2003，61：43－104.

［3］ 徐植信，翁大根，強烈地面運動持續時間對結構物倒塌的影響［J］.同濟大學學報，1982（2）：7－24.

［4］ Jeong G D，Iwan W D.The Effect of Earthquake Duration on the Damage of Structures［J］.Earthquake Engineering ＆Structural Dynamics，1988（8）：1201－1211.

［5］ 杜修力，劉勇生，強震持時對鋼筋混凝土結構地震累積破壞的影響［J］.地震工程與工程振動，1992（3）：65－70.

［6］ Julian J.Bommer，Guido Magenes，Jonathan Hancock，Paola Penazzo.The Influence of Strong－Motion Duration on the Seismic Response of Masonry Structures［J］.Bulletin of Earthquake Engineering，2004（1）：1－26.

［7］ JW Van de Lindt，GH Goh.Effect of Earthquake Duration on Structural Reliability［J］.Engineering Structures，2004（11）：1585－1597.

［8］ IunioIervolino，Gaetano Manfrediand Edoardo Cosenza.Ground Motion Duration Effects on Nonlinear Seismic Response［J］.Earthquake Engineering ＆Structural Dynamics，2006（1）：21－38.

［9］ Zhang Sherong，Wang Gaohui，Pang Bohui，et al.The Effects of Strong Motionduration on the Dynamicre Sponse and Accumulated Damage of Concrete Gravity Dams［J］.Soil Dynamics and Earthquake Engineering，2013，45：112－124.

［10］M Raghunandan，AB Liel.Effect of Ground Motion Duration on Earthquake－induced Structural Collapse［J］.Structural Safety，2013，41：119－133.

［11］中國地震動參數區劃圖［S］.國家地震局，2001.

［12］錢向東，程玉瑤.地震動持時預測方程的最新研究進展［J］.三峽大學學報：自然科學版，2013，35（2）：47－55.

［13］申愛國.地震動持續時間概率預測方法的研究［J］.內陸地震，1992（1）：115－120.

［14］汪夢甫.地震動持時的概率危險性分析方法［J］.華南地震，1996（1）：43－47.

［15］高玉峰，劉漢龍，朱 偉.基于地震危險性分析的場地地震動持時特性研究［J］.世界地震工程，2000（4）：109－112.

［16］McGuire R K，Barnhard T P.The Usefulness of Ground Motion Duration in Prediction of Severity of Seismic Shaking［C］.Proceedings，2nd US National Conference on Earthquake Engineering，Stanford，Calif，1979：713－722.

［17］Julian J.Bommer，PeterJ.Stafford，John E.Alarcon.Empirical Equations for the Prediction of the Significant，Bracketed，and Uniform Duration of Earthquake Ground Motion［J］.Bulletin of the Seismological Society of A－merica，2009（6）：3217－3233.

［18］章在墉.地震危險性分析及其應用［M］.上海：同濟大學出版社，1996.

［19］馬玉宏，趙桂峰.地震災害風險分析及管理［M］.北京：科學出版社，2008.

［20］Cornell C A.Engineering Seismic Risk Analysis［J］.Bulletin of the Seismological Society of America，1968，58（5）：1583－1606.

［21］中國地震烈度區劃圖（1990）及其說明［J］.中國地震烈度區劃圖編委會.中國地震，1992（4）：1－11.

［22］汪素云，俞言祥，高阿甲.中國分區地震動衰減關系的確定［J］.中國地震，2000（2）：99－106.