基于概率有限元法的大型LNG儲罐可靠性評估及參數(shù)敏感性分析

安　浩（陜西省天然氣股份有限公司,　西安　710016）

基于概率有限元法的大型LNG儲罐可靠性評估及參數(shù)敏感性分析

安浩
（陜西省天然氣股份有限公司,西安710016）

摘要：大型液化天然氣儲罐的安全性問題是一個十分重要的問題。因此，研究大型液化天然氣儲罐的可靠性評價方法具有重要的意義。本文以儲罐結(jié)構(gòu)的屈服強(qiáng)度為結(jié)構(gòu)抗力，以球型罐體結(jié)構(gòu)在負(fù)荷承載作用下所產(chǎn)生的最大應(yīng)力叫做荷載效應(yīng)，在建立大型液化天然氣儲罐正常使用極限狀態(tài)的狀態(tài)方程，由此得到大型液化天然氣儲罐可靠性的概率評價模型。最后，對某大型液化天然氣儲罐進(jìn)行了可靠性及參數(shù)敏感性分析。實例說明了本文方法的有效性。

關(guān)鍵詞：大型液化天然氣儲罐；安全性；可靠性；正常使用極限狀態(tài)；參數(shù)敏感性

0　引言

當(dāng)前我國已進(jìn)入能源結(jié)構(gòu)大幅調(diào)整的發(fā)展階段，天然氣以其環(huán)保、經(jīng)濟(jì)的優(yōu)點(diǎn)越來越被廣泛地使用。液化天然氣(LiquefiedNaturalGas，簡稱LNG)儲罐作為一種重要的能源存儲設(shè)備在西方發(fā)達(dá)國家得到了廣泛的應(yīng)用[1]。LNG儲罐在我國有著廣闊的應(yīng)用前景，我國建成、正在籌劃或建設(shè)中的LNG儲罐已有多處[1]。然而，大型LNG儲罐的關(guān)鍵設(shè)計技術(shù)長期被西方發(fā)達(dá)國家壟斷，我國的相關(guān)技術(shù)尚不成熟。眾所周知，儲罐是重大危險源，一旦發(fā)生有毒或易燃介質(zhì)的泄露等事故不僅會帶來大量經(jīng)濟(jì)損失，還會對生態(tài)環(huán)境造成嚴(yán)重的破壞。因此，開展大型LNG儲罐安全可靠性設(shè)計與評價已迫在眉睫。為本文以現(xiàn)有可靠度理論為依據(jù)，建立大型LNG儲罐的可靠性評價模型，提出了基于概率有限元的大型LNG儲罐可靠性評價方法。該方法不僅可以給出大型LNG儲罐的可靠概率，通過參數(shù)敏感性分析還可以揭示影響LNG儲罐安全可靠性的主要因素，可為大型LNG儲罐的可靠性設(shè)計提供參考和依據(jù)。

1　儲罐可靠性的概率評價模型

但根據(jù)強(qiáng)度失效準(zhǔn)則，儲罐在使用過程中，不允許出現(xiàn)應(yīng)力超過屈服強(qiáng)度的事件發(fā)生，如果應(yīng)力超過屈服強(qiáng)度則認(rèn)為結(jié)構(gòu)失效。因此，可以以儲罐結(jié)構(gòu)的屈服強(qiáng)度是儲罐結(jié)構(gòu)具備的抗力R，以儲罐結(jié)構(gòu)在載荷承載作用下產(chǎn)生的最大應(yīng)力作為作用效應(yīng)S建立基于強(qiáng)度失效模式的儲罐的功能函數(shù)如下：

由于儲罐結(jié)構(gòu)的作用效應(yīng)是各基本隨機(jī)變量的隱式函數(shù)，（1）式為隱式函數(shù)。

儲罐結(jié)構(gòu)的可靠概率Pf為：

2　基于概率有限元法的儲罐結(jié)構(gòu)可靠概率求解

由于LNG儲罐的結(jié)構(gòu)復(fù)雜，其結(jié)構(gòu)結(jié)構(gòu)響應(yīng)量與隨機(jī)變量間的函數(shù)關(guān)系也相當(dāng)復(fù)雜，一般的高次非線性函數(shù)不能滿足需求，其結(jié)構(gòu)功能函數(shù)基本皆為隱式，這也要求采用新的求解方法計算其可靠度。對此，我們提出了一種基于概率有限元法進(jìn)行解決。

2.1概率有限元法的基本方法原理

在桿系結(jié)構(gòu)有限元理論概念中，結(jié)構(gòu)剛度方程為：

（3）式中，H，u，f分別為剛度矩陣、節(jié)點(diǎn)位移列陣與節(jié)點(diǎn)荷載列陣。剛度矩陣是[2]：

（4）式中，B(X)、D(X,b)、u(b)、f(b)依次為應(yīng)變矩陣、材料性能矩陣、節(jié)點(diǎn)位移矩陣和節(jié)點(diǎn)荷載矩陣。X幾何坐標(biāo)，積分域，D、u、f中b(x)是隨機(jī)函數(shù)。

函數(shù)關(guān)系式中的物理量分解為隨機(jī)變量的均值和偏差，有

將（5）式展開[2]：

（7）式可以看成是一個具有平均值的確定性有限元問題，和（3）式相同，只要把每個變量的平均值代入便可由有限元方程求得出結(jié)構(gòu)節(jié)點(diǎn)位移的平均值。所以（8）式可以改寫成:

因此，由（9）式可得出位移向量的協(xié)方差：

有限元分析中單元應(yīng)力為

為了簡便，可將B看成確定性矩陣，忽略二階微量得應(yīng)力均值和應(yīng)力偏差為：

從(14)式可得各應(yīng)力分量之間的協(xié)方差矩陣[2]：

概率有限元方程式（7）是位移均值控制方程，可以采用確定性有限元方程求解；（8）式是位移波動量控制方程。假設(shè)已知荷載波動量和剛度矩陣，把可看作為荷載項，用確定性有限元法去求解位移波動量。由（13）、（14）式求解出應(yīng)力均值和波動量。

2.2統(tǒng)計模擬法（Monte -Car lo法）的基本原理

統(tǒng)計模擬法的基本原理為：在功能函數(shù)中隨機(jī)抽取N個變量，然后分別將每個變量代入函數(shù)（）中進(jìn)行驗證，若計算結(jié)果記為有效，統(tǒng)計出有效個數(shù)L，當(dāng)樣本容量足夠大時，以結(jié)構(gòu)可靠的次數(shù)L占抽樣總數(shù)N的頻率來表示結(jié)構(gòu)的可靠概率Pf，即。

2.3抽樣方法的選擇

直接抽樣的Monte-Carlo法往往出現(xiàn)抽樣數(shù)據(jù)點(diǎn)而導(dǎo)致仿真循環(huán)重復(fù)的現(xiàn)象，從而導(dǎo)致其計算效率低下，難以直接工程應(yīng)用。

拉丁超立方抽樣法在實際中應(yīng)用較為廣泛，其抽樣原理可以解釋為：假設(shè)隨機(jī)變量的抽樣次數(shù)為N；拉丁超立方抽樣法是把每一次輸入等概率地均分成N列子區(qū)間；對每一列子區(qū)間僅抽取1個樣本即，每列中樣本選取位置是隨機(jī)的[3～6]。

不難看出，采用拉丁超立方抽樣法選取的樣本是離散的分布在空間中的，且具有記憶功能，從而很好的彌補(bǔ)了直接抽樣法的不足。對比看來，拉丁超立方法的模擬次數(shù)能比直接抽樣法少近40%[5，6]。根據(jù)以上原理，本文將對拉丁超立方抽樣法和有限元相結(jié)合來求解結(jié)構(gòu)的失效概率。

3　儲罐可靠性分析

3.1工程概況及結(jié)構(gòu)有限元分析模型

某球罐，球殼內(nèi)直徑為15700mm，厚度70mm。其材料彈性模量為2.094E5Mpa，泊松比為0.3，球罐屈服強(qiáng)度為235Mpa，工作壓力為2.85Mpa，密度7.8E-6t/mm3。采用大型通用有限元軟件ANSYS建模[7]，結(jié)構(gòu)有限元模型如圖1所示。

3.2 結(jié)構(gòu)可靠性分析

可采用有限元分析軟件（ansys軟件）開展結(jié)構(gòu)有限元分析，然后在編制球罐可靠性分析ANSYS參數(shù)化設(shè)計語言（APDL語言）程序。

3.2.1隨機(jī)輸入變量的確定

設(shè)球罐內(nèi)直徑D，壁厚T，工作壓力P，屈服強(qiáng)度R，球罐密度DENSITY，材料彈性模量YOUNG，作為隨機(jī)輸入變量。隨機(jī)輸入變量的參數(shù)特征見表1。

表1　隨機(jī)輸入變量及參數(shù)特征表

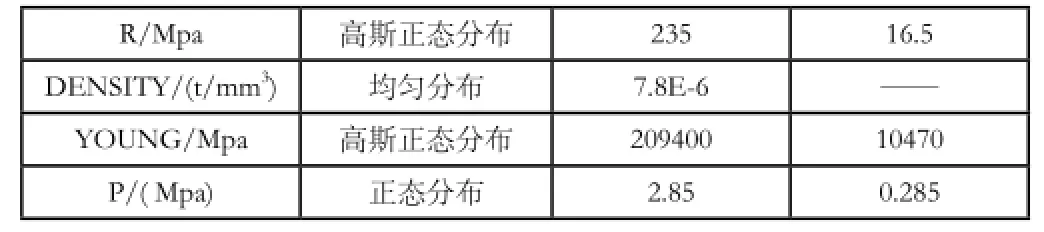
注 :密 度 DENSITY服 從 均 勻 分 布，Xmin=0.9×DENSITY，Xmax=1.1×DENSITY

3.2.2極限狀態(tài)功能函數(shù)的確定

將表2中各隨機(jī)變量帶入球罐結(jié)構(gòu)功能函數(shù)Z得到極限狀態(tài)的球罐結(jié)構(gòu)功能函數(shù)如下：

將球罐結(jié)構(gòu)極限狀態(tài)的響應(yīng)量Z作為隨機(jī)輸出變量。

3.2.3抽樣次數(shù)的確定

依照隨機(jī)輸入變量抽樣的結(jié)果可以獲得各種隨機(jī)輸入變量的頻度圖（概率密度函數(shù)圖像）。舉例展示，圖2～5只列出部分隨機(jī)輸入變量抽樣1000次得到的頻度圖。圖6和圖7分別為隨機(jī)輸出變量z的輸出的樣本均值歷史和標(biāo)準(zhǔn)差歷史。

由圖2～5可以看出：各變量抽樣得到的概率密度函數(shù)曲線與其分布類型相同，且與柱狀圖吻合較好[8]，光滑連續(xù)，表明抽樣次數(shù)選擇1000次較為合適。從圖6、7可以看出，Z樣本越趨近穩(wěn)定狀態(tài)，那么說明收斂帶寬要越來越窄，而且空間特性的反映必須是在抽樣次數(shù)足夠的情況下。因此，本文采用拉丁超立方抽樣法對各隨機(jī)輸入變量抽樣1000次對球罐進(jìn)行可靠性分析是合理的。

3.3可靠性分析結(jié)果及參數(shù)敏感性分析

3.3.1輸出變量的概率分布

可將各隨機(jī)輸入變量套入功能函數(shù)可得到隨機(jī)輸出變量Z抽樣過程狀態(tài)圖如圖8。隨機(jī)輸出變量Z的概率分布和參數(shù)特征為見9和表2。

表2　輸出參數(shù)的參數(shù)特征圖表

由圖8、9和表2可看出：輸出變量Z均值大于0，表示儲罐結(jié)構(gòu)抗力總體上大于作用效應(yīng)。同時也看出：輸出變量Z的輸出大致服從正態(tài)分布。

3.3.2球罐可靠概率

在置信度為95%時,結(jié)構(gòu)的可靠概率為9.99455e-001（99.9455%）。

3.3.3參數(shù)敏感性分析

通過參數(shù)敏感性分析可以了各輸入變量對球罐結(jié)構(gòu)可靠性影響程度的大小，得到影響結(jié)構(gòu)可靠性的主要因素。參數(shù)敏感性分析可以借助散點(diǎn)圖和靈敏度分析來完成。筆者利用ansys軟件的APDL語言提取各隨機(jī)輸入變量與輸出變量Z的相關(guān)性散點(diǎn)圖如圖10～15所示。由各參數(shù)與輸出變量Z的相關(guān)性散點(diǎn)圖得到隨機(jī)輸入?yún)?shù)對輸出變量Z的線性相關(guān)系數(shù)如表3所示。

表3　隨機(jī)輸入?yún)?shù)對輸出變量的線性相關(guān)系數(shù)

從圖10～15可以看出，隨著球罐壁厚T，球罐屈服強(qiáng)度YIES，球罐彈性模量YOUNG等變量的加大，結(jié)構(gòu)可靠概率增加。隨著球罐結(jié)構(gòu)的內(nèi)直徑D、壓力LOAD的增大，球罐結(jié)構(gòu)可靠概率會減小。

由圖10～15還可直觀地看出各隨機(jī)輸入變量與輸出變量之間的關(guān)聯(lián)性：球罐結(jié)構(gòu)的屈服強(qiáng)度YIES與球罐可靠概率的相關(guān)性最強(qiáng)，壓力LOAD次之，屈服強(qiáng)度YIES與壓力LOAD是球罐可靠性的主要影響，對其可靠性起控制作用；而球罐結(jié)構(gòu)的內(nèi)直徑D、球罐壁厚T、球罐彈性模量YOUNG等變量與球罐可靠概率相關(guān)性較小。也就是說，這些變量對球罐可靠概率的影響很小，是不顯著項。

參數(shù)靈敏度分析如圖16所展示。若輸入?yún)?shù)對輸出參數(shù)影響水平小于2.5%，表明為非明顯影響因素，若影響水平大于2.5%，則表明為明顯影響因素。從圖16還可以看出，壓力LOAD與屈服強(qiáng)度YIES是球罐結(jié)構(gòu)可靠概率的明顯影響因素，且屈服強(qiáng)度YIES的變異性對結(jié)構(gòu)失效概率的影響大于壓力LOAD。而球罐結(jié)構(gòu)的內(nèi)直徑D、球罐壁厚T、球罐彈性模量YOUNG和密度DENSITY屬于影響不大的非明顯因素。

參數(shù)敏感性分析在球罐可靠性設(shè)計中非常重要，設(shè)計者往往都是根據(jù)參數(shù)敏感性分析的結(jié)果，找出影響儲罐安全的主要因素，從而確保儲罐結(jié)構(gòu)的安全性。由以上的實例分析可以看出，屈服強(qiáng)度YIES、壓力LOAD是影響球罐結(jié)構(gòu)可靠概率的主要因素，可以通過選擇高強(qiáng)度材料和減少壓力的方式提升球罐的安全可靠性。

近些年來，大型液化天然氣儲罐在我國大量出現(xiàn)。儲罐是重大危險源，研究儲罐的安全可靠性具有重要的現(xiàn)實意義。本文首先建立儲罐安全可靠性的概率評價模型，然后利用概率有限元法對某球型儲罐進(jìn)行了可靠性大小評價和參數(shù)敏感性分析。主要得到以下成果和結(jié)論：

（1）對于液化天然氣儲罐等大型復(fù)雜工程結(jié)構(gòu)可靠性評價問題，因其結(jié)構(gòu)功能函數(shù)的隱式性可采用概率有限元法來進(jìn)行可靠性分析。

（2）通過強(qiáng)度失效準(zhǔn)則，構(gòu)建儲罐結(jié)構(gòu)的安全可靠性評價模型。通過實例分析說明該評價方法可以很好地得出影響儲罐結(jié)構(gòu)可靠概率的主要因素。從而可以為提高儲罐結(jié)構(gòu)的安全可靠性提供理論依據(jù)和有益參考。

參考文獻(xiàn)：

[1]張斌．儲罐基礎(chǔ)沉降與變形后的可靠度評價研究[D].大慶：大慶石油學(xué)院,2007．

[2]金偉婭，張康達(dá).可靠性工程[M].北京：化學(xué)工業(yè)出版社,2005.

[3]曾福強(qiáng)，朱燕軍等.基于ANSYS概率有限元的薄壁高墩靜風(fēng)可靠性分析[J].中外公路,2011(03).

[4]趙國藩,金偉良,貢金鑫.結(jié)構(gòu)可靠度理論[M].北京:中國建筑工業(yè)出版社,2000.

[5]王潔，武清璽.桿系結(jié)構(gòu)蒙特卡羅法計算及敏感性分析[J].山西建筑,200632(03).

[6]張鵬.基于Kriging模型的隧道圍巖穩(wěn)定性分析[D].長沙：湖南大學(xué)碩士學(xué)位論文,2009(05).

[7]余偉煒等.ANSYS在機(jī)械與化工裝備中的應(yīng)用[M].北京:中國水利水電出版社,2005.

[8]余文成,包惠明.基于ANSYS的水泥混凝土路面可靠性分析[J].中外公路,2007,27(02).

作者簡介：安浩（1982—），男，本科，工程師，研究方向：天然氣工程管理。