6通道MSVD構造及其在多聚焦圖像融合中的應用

劉 斌，劉維杰，魏艷萍

（1.湖北大學計算機與信息工程學院，湖北武漢430062；2.武漢大學計算機學院，湖北武漢430072）

6通道MSVD構造及其在多聚焦圖像融合中的應用

劉 斌1，劉維杰2，魏艷萍1

（1.湖北大學計算機與信息工程學院，湖北武漢430062；2.武漢大學計算機學院，湖北武漢430072）

針對經典的奇異值分解（singular value decomposition，SVD）在圖像處理中的不足，提出了一種6通道多尺度奇異值分解（multi-scale SVD，MSVD）的構造方法，并將其應用于多聚焦圖像融合中。首先，在經典SVD的基礎上，利用矩陣分塊的方法，給出了一種6通道MSVD的構造方法。其次，對參加融合的多聚焦圖像進行6通道MSVD分解，得到高層低頻和各層5個方向的高頻，對分解的低頻子圖像采用取平均、高頻子圖像采用區域能量取大的融合規則進行融合，并進行MSVD逆變換得到融合結果圖像。最后，對融合結果圖像進行主觀分析和客觀評價。實驗結果表明該方法有好的視覺效果，融合結果圖像有較高的清晰度和較豐富的邊緣細節信息，且沒有方塊效應。從客觀指標看，該方法有較高的清晰度和空間頻率，其清晰度和空間頻率比基于離散小波變換、基于提升小波變換、基于曲波變換和基于輪廓波變換的融合方法都高。

圖像融合；矩陣奇異值分解；多尺度分析；多聚焦圖像

0 引 言

多聚焦圖像融合攝取多幅數字圖像的較清晰部分，形成一幅各處清晰的新圖像，新的圖像可以獲得場景目標更可靠、全面和更準確的信息，可為計算機進行后續的圖像處理提供更清晰的結果圖像。近年來，多聚焦圖像融合得到了較廣泛的發展和應用［1-2］，目前，多聚焦圖像融合方法層出不窮，其中，基于多尺度分析的融合方法因其優越的性能而成為多聚焦圖像融合方法的主流。自文獻［3］提出了圖像的金字塔構造方法并應用于圖像編碼后，各種基于金字塔的圖像融合方法被提出，這些金字塔主要有拉普拉斯金字塔［4］、對比度和比率金字塔［56］。張量積小波多尺度分析也是一種金字塔方法，它是具有方向性的金字塔，也被廣泛應用于圖像融合中［78］。近年來，為了解決張量積小波在圖像處理方向上的不足，一些新的基于小波多尺度分析的多聚焦圖像融合方法被提出，這些新的小波有多尺度形態學小波［9］，曲波（curvelet）［10-11］，采樣和非下采樣輪廓波（contourlet）［12-13］，采樣和非下采樣提升小波（lifting wavelet）等［1416］。基于金字塔的融合方法雖然能實現圖像的多尺度融合，但這些方法都不具有方向性，且融合結果圖像中會出現人工痕跡和方塊效應。基于張量積小波的融合方法雖然具有方向性，但其只注重圖像中的水平方向和垂直方向的邊緣信息，且由于對濾波后的圖像分別進行行、列的下2抽樣，使得結果圖像中不可避免地會產生方塊效應；基于多方向的一類新的小波雖然能提取圖像中多個方向的高頻信息，但其本質上還是張量積小波，且都依賴于Fourier變換，而且融合時的運算量偏大；基于提升小波的圖像融合方法在空間域內進行，不依賴于Fourier變換，速度快，適合于實時圖像融合，但目前所使用的提升小波實際上還是張量積小波，它不是二維小波變換的一般形式，因而也只能提取圖像中的水平方向和垂直方向的邊緣信息，且也不可避免地會產生方塊效應。

矩陣或圖像的奇異值分解（singular value decomposition，SVD）［17］是一種正交變換，具有高度去相關性，能把信息集中到矩陣的少數行或列上。此方法近年來在圖像識別與處理中得到廣泛應用。它有如下特點：①能量集中與重新分配。圖像的SVD分解是將圖像矩陣按特征值的大小對其進行對角化分解，體現了圖像能量從大到小的分布特點，主要能量集中于圖像的重新處理地后的少數向量上，也就是體現了其主成份分析特性。這種SVD有很好的穩定性，即當圖像的灰度值有較小的改變時，圖像的奇異值也不會發生較大的變化。SVD既是圖像的內蘊特征的表現，也體現了圖像能量從大到小的分布規律性，從頻率分布的角度看，這種能量從大到小的分布規律也體現了圖像頻率從低頻到高頻的分布規律，因而其分解也具有明顯的物理意義，也可看成是頻率的分解；②具有正交性。能消去像素間的相關性。它使得變換后的圖像沒有冗余性，因而更適合于圖像壓縮和融合；③在時域內完成，不需要進行Fourier變換，但也能體現頻率特征，有高頻和低頻；④速度快，能進行實時分解與融合，無需卷積運算，具有線性計算復雜性。

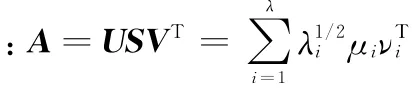
1 SCMSVD構造

1.1 矩陣的SVD

對實數矩陣A∈Rm×n，存在兩個正交矩陣U∈Rm×m和V∈Rn×n，使得

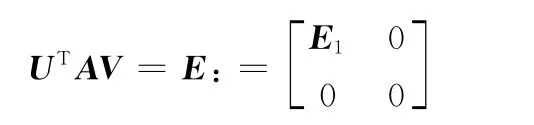
從而矩陣A可分解成3個正交矩陣的乘積，即

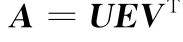
式中，E1是大小為m×n的對角陣。若A的秩為r，則E1的對角線上的元素可排列為

顯然，A和E1是等價的。因為

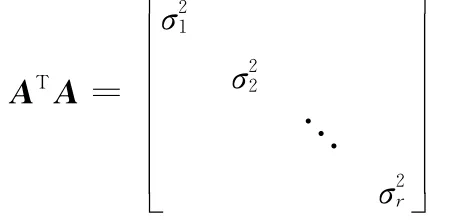
即E1的對角線上元素的值是矩陣A的特征值的均方根，這些元素稱為A的奇異值。其有較好的穩定性，即當矩陣A的元素的值有較小變化時，其奇異值的改變也不大。奇異值越大，其對應的特征向量擁有的信息量就越多。大的奇異值對應圖像的近似部分，即低頻部分。而較小的值就對應著圖像的細節部分，即圖像中的高頻部分。因此，如果能將參加融合的圖像按照奇異值大小分離出近似信息和細節信息，那么就可以構造出融合圖像的多尺度分析［19］。

1.2 SCMSVD構造

為了建立圖像的6通道多尺度分析，首先對圖像進行分塊，對分塊后的圖像進行分類，形成分類矩陣，計算分類矩陣的奇異值分解，從而構造出一種圖像的6通道多尺度分析，具體步驟如下：

步驟1 將圖像X∈Rm×n按從上到下、從左到右的方式分成大小為p×q的子塊，得到矩陣塊序列X（k，l）（1≤k≤m／p，1≤l≤n／q）；

步驟2 將每個子塊按先行后列的方式展開為（（p× q）×1）的列向量，再將這些列向量的各元素組合成為一個（p×q）×（mn／（p×q））大小的矩陣T；

步驟3 對T進行SVD分解：T＝USVT，其中U是大小為（p×q）×（p×q）的正交矩陣，V是大小為（mn／（p×q））2的正交矩陣。

步驟4 用得到的UT對T進行線性正交變換（相乘），得大小為（p×q）×（mn／（p×q））的矩陣A，即

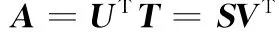
步驟5 完成步驟2的逆操作。將A的各個列向量重新排成p×q的子塊X，共有mn／（p×q）個子塊，將它們重新組合成一個m×n的矩陣X2。

通過上述分解過程后可得到1個低頻子圖像和（p× q－1）個高頻子圖像。矩陣A的每一行是正交矩陣U作用于T的結果，U的列向量與奇異值一一對應，U的第一列是最大的奇異值所對應的特征向量。作用后的A的第一行就包含了原圖像的主要能量，它是原圖像分解出的近似部分，即低頻圖像。同理，A中其他行包含圖像較少的能量，是圖像的細節部分，即高頻圖像。這樣便實現了圖像的多尺度分解。這樣，通過步驟4得到矩陣A后，將A的每一行提取出來按先列后行的順序重新排列成一個（m／p）×（n／q）的矩陣，分別記為A1，A2…A（p×q），A1就是低頻子圖像，其他都是高頻子圖像。

本文中當p×q＝6時就得到6通道的圖像分解，由于2×3＝6且3×2＝6，因此，可采用2×3或3×2的方塊方式，分解后可得到6幅圖像：1個低頻子圖像和5個高頻子圖像，分別記作A1，D1，D2，D3，D4，D5。

重構過程是上述分解過程的逆過程。將分解得到的p×q個（m／p）×（n／q）矩陣分別按行、列展開，再組合成（p×q）×（mn／（p×q））的矩陣A*，保留分解時U的值，計算T*＝UA*，然后將T*的列向量還原成p×q的塊，再將這些塊重新組合，得到一個m×n的重構圖像X*。

上述過程只是對圖像進行一層SVD分解，對低頻子圖像A1按上述方式類似地進行多層分解，即得到圖像的MSVD構造。

2 圖像融合算法

基于6通道MSVD的圖像融合流程如圖1所示，其主要步驟如下：

步驟1 對參加融合的兩幅或多幅多聚焦圖像進行位置配準。

步驟2 按第1節的方式分別對參加融合的原圖像進行多級6通道MSVD分解，得到最高層一個低頻子圖像和各層5個高頻子圖像。

步驟3 對分解后的最高層低頻子圖像和各層高頻子圖像按不同融合規則進行融合。

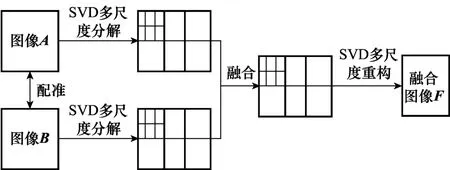
圖1 基于SCMSVD的圖像融合流程

圖像進行MSVD后的低頻系數體現的是圖像中的近似信息，低頻系數越小，表示圖像中的低頻成分越少，就此而言，低頻系數越小越好，然而，低頻成份是圖像中的主要能量的體現，系數過小，則能量較小，圖像的亮度會越低，另外，為了使融合結果圖像能盡可能保持參加融合圖像的能量的均衡，一般取兩幅圖像分解后的最高層（空間分辨率最低）的低頻系數的平均作為融合結果圖像的低頻，設A、B分別為參加融合的兩幅多聚焦原圖像，記A分解后的低頻圖像為AJ，l，B分解后的低頻圖像為BJ，l，對所有低頻像素點（m，n），則融合圖像的低頻FJ，l為

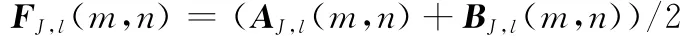
為了使融合結果圖像充分體現原圖像中的清晰部分，選擇融合系數時，就要選擇能體現原圖像進行MSVD分解后能體現原圖像清晰部分的系數。圖像進行MSVD分解后的高頻系數的特性和作用與其他的多尺度分析融合方法的高頻系數的方法相同［20］，在對高頻圖像進行融合時，要盡可能選擇絕對值較大的系數作為融合高頻子圖像的系數。另外，由于圖像中的有效目標是以像素塊的形式存在的，因此，融合時必須考慮把中心像素和其周圍的區域內的像素一起融合，因此，本文對圖像MSVD分解的各層高頻系數采用基于區域能量取大的融合規則，這樣既能很好地考慮圖像的清晰度和亮度，又能較好地表現圖像中的目標。即圖像MSVD分解后的高頻系數的融合規則如下：

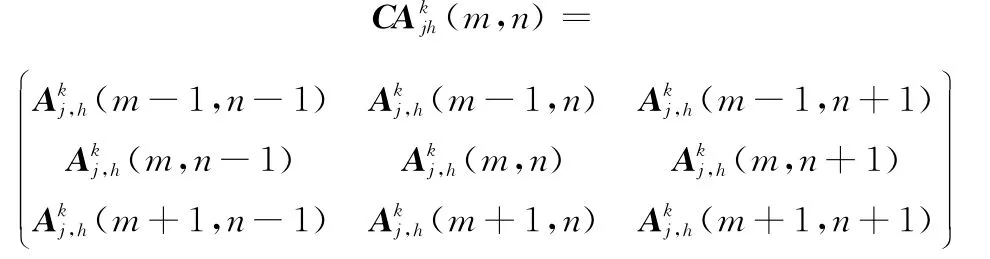
定義這個窗口的能量為

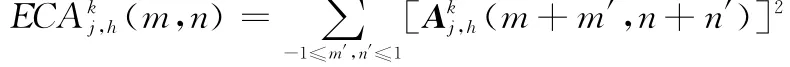
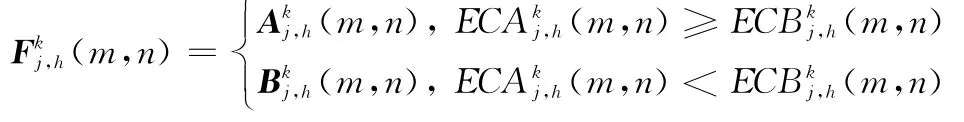
步驟4 對圖像分解后的不同層的正交矩陣U進行融合。

U相當于圖像分解和重構過程的基，為了使基的作用在參加融合的圖像中盡可能平衡，選擇參加融合圖像分解后的各層的兩個U的平均值作為融合結果U的值，具體融合方式如下：

對參加融合的圖像A、B，記UA，j為A的第j層分解后的正交矩陣，UB，j為B的第j層分解后的正交矩陣，則第j重構的正交構矩陣為

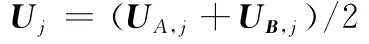
步驟5 按第1節的重構方式對融合后的MSVD塔形結構進行逆變換，得最終融合結果圖像。

3 實驗結果分析與評價

3.1 實驗結果

大量實驗結果證實了上述方法是可行而有效的，這里列出實際多聚焦和模擬多聚焦兩類圖像（每類兩組圖像）的實驗結果，第1類為實際多聚焦圖像的融合實驗，第2類為模擬多聚焦圖像及其融合實驗。第1組和第2組為2對實際多聚焦圖像的融合實驗，其中第1組的源圖像如圖2（a）、圖2（b）所示，是Clock圖像，圖像大小均為512×512，圖2（a）是聚焦左邊小鐘的圖像，圖2（b）是聚焦右邊大鐘的圖像；第2組的源圖像如圖3（a）、圖3（b）所示，是Disk圖像，圖像大小均為480×640，圖3（a）是聚焦右邊鐘的圖像，圖3（b）是聚焦左邊磁盤的圖像。第3組和第4組為模擬多聚焦圖像融合實驗，選定的2幅清晰的標準圖像分別如圖4（a）和圖5（a）所示，圖4（a）是大小為512×512的清晰的Lena圖像，圖5（a）是大小為512×512的清晰的Peppers圖像，利用文獻［5］的方法分別產生模擬多聚焦圖像。圖4（b）和圖4（c）分別為通過此方法對圖4（a）的Lena圖像分別進行聚焦于左邊和聚焦于右邊的圖像，圖5（b）和圖5（c）分別為通過此方法對圖5（a）的Peppers圖像分別進行聚焦于下面和聚焦于上面的圖像。圖2（g）、圖3（g）、圖4（h）和圖5（h）分別是利用本文方法對圖2（a）和圖2（b）、圖3（a）和圖3（b）、圖4（b）和圖4（c）、圖5（b）和圖5（c）進行融合的結果圖像。

圖2 Clock實際多聚焦圖像融合

圖3 Disk實際多聚焦圖像融合

圖4 Lena模擬多聚焦圖像融合

為了體現本文方法的融合優勢和特點，基于（discrete wavelet transform，DWT）［8］、基于（lifting wavelet transform，LWT）［14］、基于（curvelet transform，CT）［11］以及基于（contourlet transform，CTT）等的融合方法［12］分別與本文方法進行對比研究，這4種方法的融合規則與本文融合規則相同。圖2（c）～圖2（f）分別是Clock圖像分別使用這4種方法得到的融合結果圖像，圖3（c）～圖3（f）分別是Disk圖像分別使用這4種方法得到的融合結果圖像，圖4（d）～圖4（g）分別是Lena圖像分別使用這4種方法得到的融合結果圖像，圖5（d）～圖5（g）分別是Peppers圖像分別使用這4種方法得到的融合結果圖像。DWT方法和CTT方法所采用的張量積小波均為Daubechies系列小波中的db2小波。LWT方法使用db2小波的提升小波，基于CTT融合方法所使用的方向濾波器為5－3方向濾波器，所有參與比較的5種方法對源圖像的分解層數均為3，使用Matlab7.5編程實現。

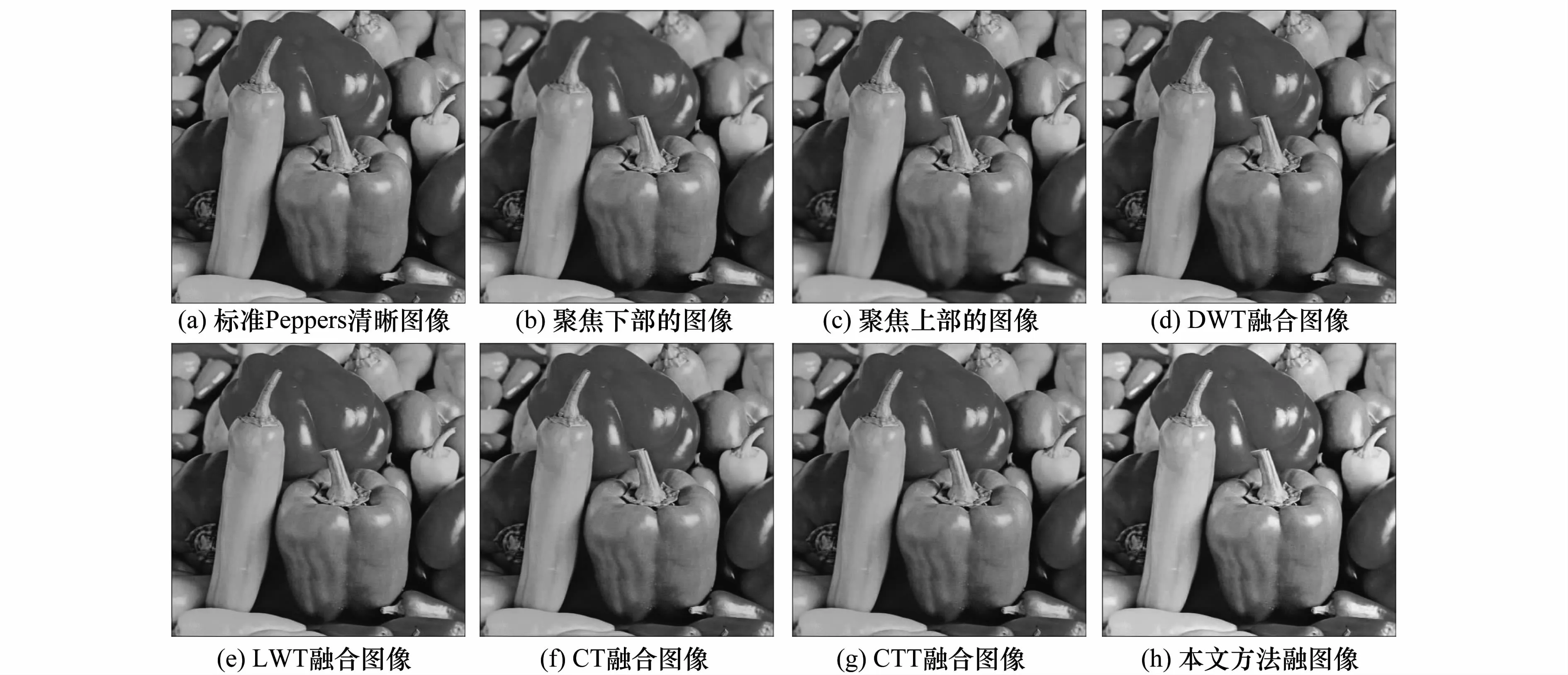
圖5 Peppers模擬多聚焦圖像融合

從融合結果圖像可以看出，圖2（g）的兩個鐘都很清晰，圖3（g）的Disk和鐘都清晰，圖4（h）的Lena圖像的左右都很清晰，圖5（h）的Peppers圖像的上下都很清晰。分別比較圖2（g）與圖2（c）～圖2（f）、圖3（g）與圖3（c）～圖3（f）、圖4（h）與圖4（d）～圖4（g）以及圖5（h）與圖5（d）～圖5（g）的融合效果可以看出，本文方法所得結果圖像有較好的對比度和清晰度。為了更看清本方法的清晰效果，對融合結果圖像使用Canny邊緣提取算子分別提取邊緣信息，并進行比較。邊緣信息越豐富，表明所在融合方法的結果圖像越清晰，這里主要列出第一組和第二組實際多聚焦融合中本文方法和基于CTT融合方法的邊緣結果圖，圖2（h）和圖2（i）分別是圖2（f）和圖2（g）的邊緣圖像，圖3（h）和圖3（i）分別是圖3（f）和圖3（g）的邊緣圖像，比較邊緣圖像可以明顯看出，本文提出的基于MSVD的融合結果圖像有較好的邊緣信息，文中邊緣圖像中有明顯不同特征的地方都被做上了黃色橢圓標記，可以看出，本文建議方法所提取的邊緣更連續、更豐富，從而說明本文方法融合結果更清晰。

3.2 客觀性能比較

為了看出各種方法的融合效果，選用圖像的清晰度、空間頻率指標去衡量各種融合方法的清晰度［21］。

清晰度是利用圖像在各點處的圖像的水平方向和垂直方向的差分平方和去衡量圖像的清晰度的，一幅圖像F的清晰度定義為

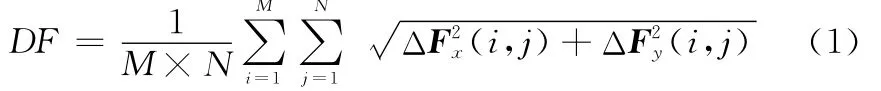
式中，ΔFx和ΔFy分別表示圖像F在x方向和y方向的差分。清晰度的值越大，圖像中有較大變化的像素點越多，結果圖像越清晰。

圖像的行頻率定義為

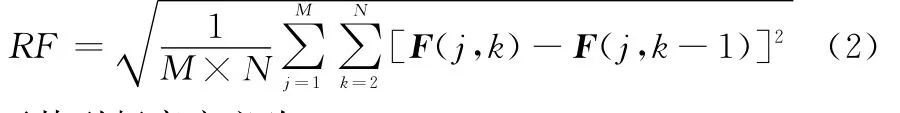
而其列頻率定義為

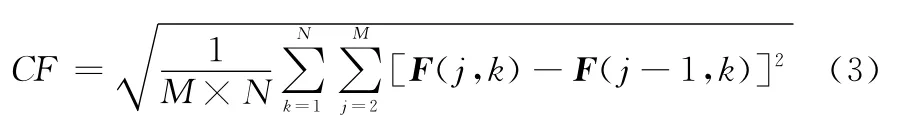
圖像的空間總頻率是行頻率和列頻率和合成，即

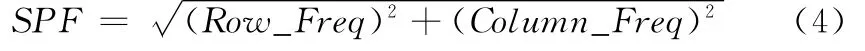
頻率越高，圖像的空間分辨力越好，圖像越清晰。

表1列出了第1組和第2組實際多聚焦圖像的融合性能指標，表2列出了第3組和第4組模擬多聚焦圖像的融合的性能指標。比較表1和表2的兩列數據可以看出，本文建議的融合方法比采用同樣融合規則的基于DWT、基于LWT、基于CT和基于CTT融合方法有較高的清晰度和空間頻率。

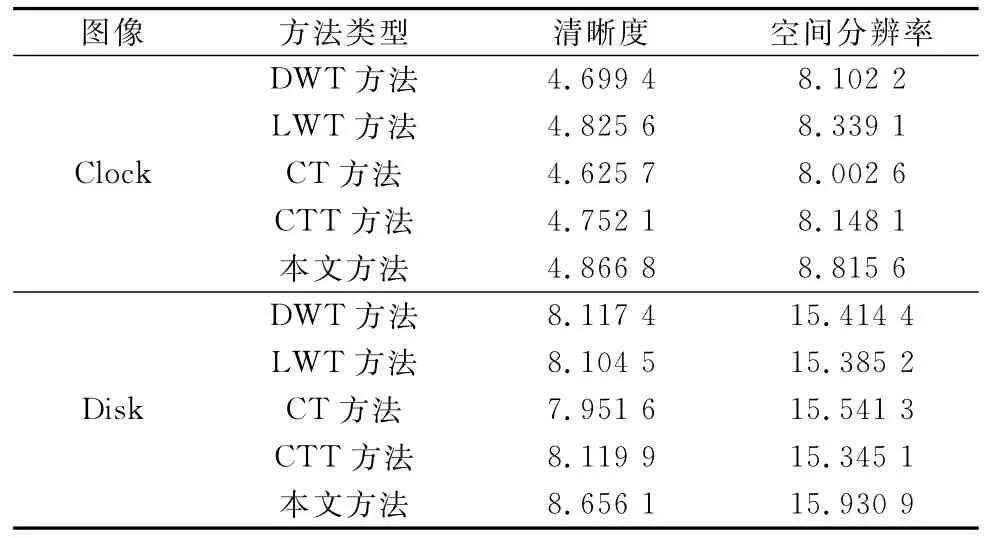
表1 實際多聚焦圖像融合性能評價

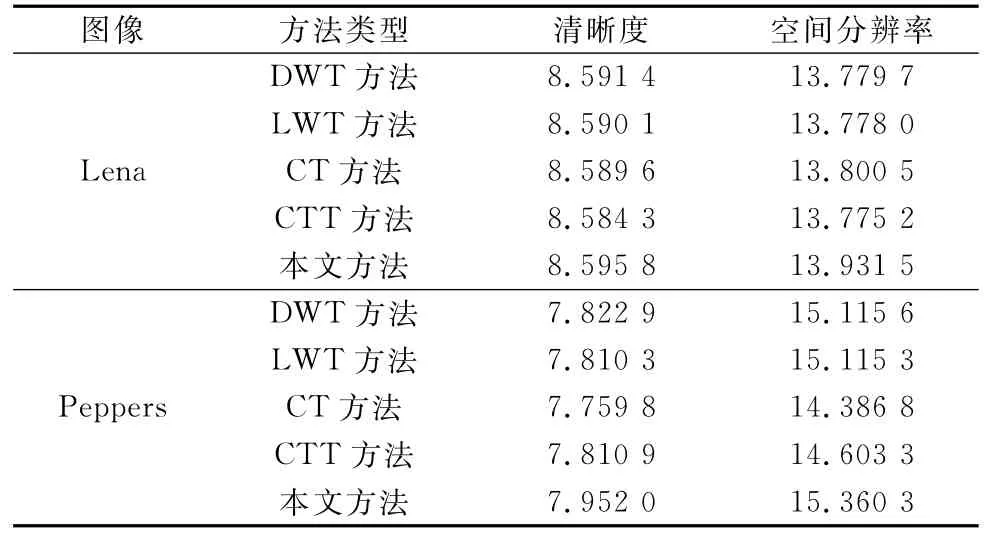
表2 模擬多聚焦圖像融合性能評價

4 結 論

提出了一種SCMSVD的構造方法，并把它應用于多聚焦圖像融合中。這種多尺度構造方法能把圖像分解到不同的尺度上，從而對圖像的低頻和高頻可以在不同頻率上的輪廓和細節進行融合處理，使融合效果更符合人的視覺特性，同時，圖像在不同層分解的5個高頻使融合結果圖像有更多更好的方向性。另外，這種多尺度分析還保留了SVD的正交性，使得圖像分解無冗余；再者，對圖像的分解與重構只在空域內完成，不依賴于Fourier變換，從而使圖像融合有較快的速度。實驗結果表明，該圖像融合方法有較好的視覺效果，結果圖像有較高的清晰度，邊緣細節信息豐富，沒有方塊效應。從客觀性能指標看，該方法有較高的清晰度和空間頻率，其清晰度和空間頻率比基于DWT、基于LWT、基于CT和基于CTT的融合方法都高。

［1］Bahador K，Alaa K，Fakhreddine O K，et al.Multisensor data fusion：a review of the state-of-the-art［J］.Information Fusion，2013，14（1）：28-44.

［2］Goshtasby A A，Nikolov S.Image fusion：advances in the state of the art［J］.Information Fusion，2007，8（2）：114-118.

［3］Burt P T，Adeson E H.The laplacian pyramid as a compact image code［J］.IEEE Trans.on Communications，1983，31（4）：532 -540.

［4］Yun S H，Kim J H，Kim S K.Image enhancement using a fusion framework of histogram equalization and laplacian pyramid［J］.IEEE Trans.on Consumer Electronics，2010，56（4）：2763-2771.

［5］Liu G X，Yang W H.A Multiscale contrast-pyramid-based image fusion scheme and its performance evaluation［J］.Acta Optica Sinica，2001，21（11）：1336-1342.（劉貴喜，楊萬海.基于多尺度對比度塔的圖像融合方法及性能評價［J］.光學學報，2001，21（11）：1336-1342.）

［6］Toet A.Multiscale contrast enhancement with application to image fusion［J］.Optical Engineering，1992，31（5）：1026-1031.

［7］Li H，Manjunath B S，Mitra S K.Multi-sensor image fusion using the wavelet transform［J］.CVGIP：Graphical Models and Image Processing，1995，57（3）：235-245.

［8］Pajares G，Cruz G J.A wavelet-based image fusion tutorial［J］.Pattern Recognition，2004，37（9）：1855-1872.

［9］Jiang Y，Wang M H.Image fusion with morphological component analysis［J］.Information Fusion，2014，18（7）：107-118.

［10］Li S T，Yang B，Hu J W.Performance comparison of different multi-resolution transforms for image fusion［J］.Information Fusion，2011，12（2）：74-84.

［11］Wang G，Ma M Z，Zhao Y L，et al.Algorithm for image fusion in the Curvelet transform domain［J］.Chinese Journal of Scientific Instrument，2008，29（9）：1841-1845.（王剛，馬美仲，趙英路，等.Curvelet變換域的圖像融合算法［J］.儀器儀表學報，2008，29（9）：1841-1845.）

［12］Liu K，Guo L，Chang W W.Regional feature self-adaptive image fusion algorithm based on contourlet transform［J］.Acta Optica Sinica，2008，28（4）：681-686.（劉坤，郭雷，常威威.基于Contourlet變換的區域特征自適應圖像融合算法［J］.光學學報，2008，28（4）：681-686.）

［13］Zhang Q，Guo B L.Multifocus image fusion using the nonsubsampled contourlet transform［J］.Signal Processing，2009，89（7）：1334-1346.

［14］Xiao X H，Wu Z H.Image fusion based on lifting wavelet transform［C］∥Proc.of the International Symposium on Intelligence Information Processing and Trusted Computing，2010：659-662.

［15］Geng G Z，Chen H，Liu Y Y，et al.Image fusion method of 9／7 wavelet transform based on lifting scheme［C］∥Proc.of the IEEE International Symposium on Knowledge Acquisition and Modeling Workshop，2008：522-524

［16］Chai Y，Li H F，Guo M Y.Multifocus image fusion scheme based on features of multiscale products and PCNN in lifting stationary wavelet domain［J］.Optics and Communications，2011，284（5）：1146-1158.

［17］Liu R Z，Tan T N.SVD based digital watermarking method［J］.Acta Electronica Sinica，2001，29（2）：168-171.（劉瑞禎，譚鐵牛.基于奇異值分解的數字圖像水印方法［J］.電子學報，2001，29（2）：168-171.）

［18］Wang X B，Liu B.Multi-focus image fusion based on multi-resolution singular value decomposition［J］.Chinese Journal of Quantum Electronics，2014，31（3）：257-263.（汪曉波，劉斌.基于多分辨奇異值分解的多聚焦圖像融合［J］.量子電子學報，2014，31（3）：257-263.）

［19］Kakarala R，Ogunbona P O.Signal analysis using a multiresolution form of the singular value decomposition［J］.IEEE Trans.on Image Processing，2001，10（5）：724-735.

［20］Liu B，Liu W J，Ma J L.Multi-focus image fusion based on three channel nonseparable symmetrical wavelets［J］.Chinese Journal of Scientific Instrument，2012，33（5）：1110-1116.（劉斌，劉維杰，馬嘉利.基于三通道不可分對稱小波的多聚焦圖像融合［J］.儀器儀表學報，2012，33（5）：1110-1116.）

［21］Eskicioglu A M，Fisher P S.Image quality measure and their performance［J］.IEEE Trans.on Communication，1995，43（12）：2959-2965.

Construction of the six channel multi-scale singular value decomposition and its application in multi-focus image fusion

LIU Bin1，LIU Wei-jie2，WEI YAN-ping1
（1.School of Computer and Information Engineering，Hubei University，Hubei Wuhan 430062，China；2.Computer School，Wuhan University，Wuhan 430072，China）

In order to solve the deficiencies of classical singular value decomposition（SVD）in image processing，a construction method of the six channel multi-scale singular value decomposition is presented.An image fusion method based on the multi-scale SVD（MSVD）is proposed.Firstly，based on the principle of classical SVD and blocking algorithm，the six-channel MSVD is performed.Secondly，the images involved in the fusion are decomposed into one approximation and five detail images with different resolution by the MSVD.The fusion rule is that the average value is selected for low-frequency sub-image；while for the high-frequency subimages，the coefficients with larger area energy value are employed.The fused image is obtained by using reconstruction method of the MSVD.Finally，the fusion performance of the result image is evaluated using subjective analysis and objective indices.The experimental results show that the proposed fusion method has good visual effect and has no blocking-artifact in the fused images.When compared with the fusion method based on discrete wavelet transform，lifting wavelet transform，curvelet transform and contourlet transform，the proposed method has been observed to have higher definition and spatial frequency.

image fusion；matrix singular value decomposition（SVD）；multi-scale analysis；multifocus image

N 911.73 文獻標志碼：A DOI：10.3969／j.issn.1001-506X.2015.09.35

劉 斌（1963 ），男，教授，博士，博士研究生導師，主要研究方向為圖像融合、模式識別。

E-mail：liub＠hubu.edu.cn

劉維杰（1991-），男，博士研究生，主要研究方向為信息安全、圖像處理。E-mail：lwj20090716＠163.com

魏艷萍（1993-），女，本科，主要研究方向為圖像處理。

E-mail：wyp20140616＠163.com

1001-506X（2015）09-2191-07

2014-09-16；

2015-01-16；網絡優先出版日期：2015-05-04。

網絡優先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150504.0941.004.html

國家自然科學基金（61471160）；湖北省自然基金重點項目（2012FFA053）資助課題