基于尾指數(shù)方法的外匯市場風險度量研究
——以美元、港幣、日元和歐元對人民幣匯率為例＊

潘雪艷，蔡光輝，劉順祥

（1．浙江工商大學統(tǒng)計與數(shù)學學院，杭州310018；2．安徽師范大學數(shù)學計算機科學學院，安徽蕪湖241003）

基于尾指數(shù)方法的外匯市場風險度量研究
——以美元、港幣、日元和歐元對人民幣匯率為例＊

潘雪艷1，2，蔡光輝1，劉順祥1

（1．浙江工商大學統(tǒng)計與數(shù)學學院，杭州310018；2．安徽師范大學數(shù)學計算機科學學院，安徽蕪湖241003）

匯率；VaR；EVT；GARCH類模型；尾指數(shù)

結(jié)合Iglesias給出的新的估計尾指數(shù)方法和Hill估計尾指數(shù)方法，將極值理論和GARCH類模型相結(jié)合，分析了2006年1月4日至2013年11月5日期間美元、港幣、日元和歐元對人民幣匯率的日對數(shù)收益率序列，并在不同的方法下分別預測了它們的VaR（風險值）。結(jié)果表明對于日元，利用新估計方法預測VaR更合適；而對于美元、港幣和歐元，Hill估計法更有優(yōu)勢。

隨著極端事件的發(fā)生而對整體金融機構(gòu)的風險產(chǎn)生的重大影響越來越受到重視，很多學者將極值理論引入到針對外匯市場的研究中。Koedijk等（1990），Hols和de Vries（1991），Wagner和Marsh（2005）［1］揭示了利用重尾分布對外匯市場的匯率波動率進行建模的優(yōu)勢。Payaslioglu（2009）利用極值理論中Hill估計法分析了土耳其匯率的波動性，從而預測土耳其是否會發(fā)生經(jīng)濟危機或危機是否已經(jīng)開始。

另一方面，Engle（1982）構(gòu)建的ARCH模型和Bollerslev（1986）構(gòu)建的GARCH模型也被廣泛的應(yīng)用于針對外匯市場匯率波動的建模中。Hill（2010）［2］指出Hill（1975）［3］估計對于GARCH模型是穩(wěn)健的，但Kearns和Pagan（1997），Wagner和Marsh（2005）等學者證明了Hill估計在樣本容量比較小時效果不是很好。Mikosch和Starica（2000）［4］利用Breiman（1965）提供的分析混合分布尾部的方法，給出了GARCH（1，1）模型的尾指數(shù)應(yīng)滿足的條件，從而為計算GARCH類模型的尾指數(shù)提供了方法。在Starica和Pictet（1997），Berkes等（2003）所做的研究以及Glosten等（1993）提出的GJR—GARCH模型的基礎(chǔ)上，Iglesias和Linton（2009）［5］給出了一個替代Hill估計的新估計方法，Iglesias（2012）［6］利用上述新的估計方法對外匯市場的7種主要貨幣對美元的匯率進行了研究，并指出對于英鎊對美元的匯率日收益率序列而言，新的估計要比Hill估計優(yōu)。

由于國外的學者研究外匯市場時，大多選擇美元為基準，考慮世界幾個主要貨幣如歐元、英鎊、日元、加拿大元等對美元的匯率波動情況，對我國涉外公司和金融機構(gòu)規(guī)避匯率波動帶來的風險，沒有太多的直接指導意義。從而很有必要以人民幣為基準，對主要幾種貨幣的匯率進行研究，為我國政府和涉及外匯業(yè)務(wù)的機構(gòu)更好的規(guī)避匯率風險提供理論依據(jù)。

國內(nèi)不少學者對我國外匯市場匯率波動率的研究大多采用的是BMM、POT等等傳統(tǒng)的極值理論，GARCH類模型，或者是假設(shè)殘差服從GPD分布的EVT—GARCH類模型等。葉五一，張明，繆柏其［7］使用尾部指數(shù)回歸方法對滬深300指數(shù)進行了研究；茍紅軍，陳迅，花擁軍［8］采用極值理論中的超閾值模型和Copula理論研究了外匯投資組合風險。Yanping Yia，Xingdong Feng，Zhuo Huang［9］結(jié)合分位數(shù)GARCH模型和極值理論利用、Monte Carlo方法模擬預測了風險值。

單純的GARCH類模型沒有考慮極端值的影響，從而導致這樣的研究對極端事件可能導致的風險估計不足，常常會低估匯率波動帶來的風險。另外，這些常用的傳統(tǒng)極值理論進行研究時需要假設(shè)序列尾部是獨立同分布的，鮮有將尾部相依性考慮進去，而事實上幾種重要外匯對人民幣匯率的數(shù)據(jù)上尾部有一定的相依性；另一方面?zhèn)鹘y(tǒng)極值理論能適用要求樣本量較大，但由于本文采用的數(shù)據(jù)是以人民幣為基準的匯率，合適的樣本量遠少于以美元為基準的樣本量。從而純粹采用傳統(tǒng)極值理論對我國外匯市場的極端風險進行估計不一定合適，為了克服以上不足，本文結(jié)合Iglesias（2010）新的估計尾指數(shù)方法和Hill（1975）估計尾指數(shù)方法，將極值理論和GARCH類模型相結(jié)合，分析了2006年1月4日至2013年11月5日期間美元、港幣、日元和歐元對人民幣匯率的日對數(shù)收益率序列，并在不同的方法下分別預測了它們的VaR值。結(jié)果表明，由Hausman類型的檢驗結(jié)果可知，對于日元而言，基于Hill（1975）估計尾指數(shù)方法得出的估計值應(yīng)該更準確，即應(yīng)用一種更加無偏的估計無疑對于預測日元來說更加具有優(yōu)勢；而就美元、港幣和歐元而言，使用Hill估計法更合適。

1 模型介紹和參數(shù)估計

1．1 GARCH類模型

廣義自回歸條件異方差（GARCH）模型是在1982年Engel引入的自回歸條件異方差（ARCH）模型基礎(chǔ)上，由Bllerslev［10］于1986年提出的。它主要是針對波動率建模，解決了殘差異方差問題，并逐步形成了以GARCH模型為核心的GARCH模型族，大量實證研究表明對大部分金融數(shù)據(jù)用GARCH（1，1）模擬效果較好。一個經(jīng)典的GARCH（1，1）模型的具體形式為：

其中εt是一個白噪聲過程。

GARCH（1，1）模型沒有考慮到市場有可能存在的非對稱性，為了更好地刻畫金融時間序列中存在的非對稱性，Glosten等（1993）［11］在GARCH模型的基礎(chǔ)上，構(gòu)造了GJR—GARCH模型，很多實踐表明這個模型是非常有用的，它的具體結(jié)構(gòu)如下：

該模型中的δγ2t－1l｛γ－1＜0｝可以很好的刻畫一些新興的不成熟市場中正面和負面信息對市場產(chǎn)生的影響的不對稱性，即負面信息 （如收益率為負等）對市場的影響會更大些。

1．2 極值理論（EVT）

極值理論 （EVT）是主要用來研究隨機變量的極值分布及其特征的理論，對隨機變量的分布函數(shù)的重尾現(xiàn)象有突出的針對性，它不需要假設(shè)總體的分布，利用樣本的數(shù)據(jù)推斷出總體分布的尾部特征。將EVT理論應(yīng)用到風險管理可以彌補傳統(tǒng)方法中VaR對極端事件關(guān)注的不足，有利于更精確的度量金融極端風險。

在應(yīng)用極值理論時使用比較多的是BMM模型和POT模型，但BMM模型要求樣本容量很大，而且由于最終分析時只取分組后的每組中的最大值 （或最小值），這樣會造成數(shù)據(jù)的大量浪費，即沒有充分分析已有的信息，本文考慮到對每種貨幣采樣的數(shù)據(jù)只有1902個，樣本容量不夠大，就沒有采用BMM模型。Pickands（1975）指出在屬于一般極值分布的吸引場內(nèi)，分布函數(shù)超過一定閾值的尾部數(shù)據(jù)服從廣義Pareto分布（GPD），從而產(chǎn)生了POT模型。Leadbetter等（1983）［12］給出在獨立同分布的假設(shè)下，最大順序統(tǒng)計量標準化漸近分布是極值分布的充要條件，Leadbetter等（1983）也證明了序列在滿足一定相依條件下，最大順序統(tǒng)計量的標準化漸近分布仍是極值分布，為POT模型的廣泛應(yīng)用提供了理論依據(jù)。POT方法中閾值的選擇有多種方法，如基于 “平均剩余壽命圖”法等，本文參照Iglesias（2012）選取自大到小的0．1T（T為樣本容量）個數(shù)據(jù)為超閾值部分。

本文記POT模型中尾指數(shù)為參數(shù)κ1，而計算POT模型中尾指數(shù)比較經(jīng)典的方法是Hill估計，記由Hill方法估計得到的各種貨幣匯率收益率序列的尾指數(shù)為是κ1的一個估計值，稱為Hill估計值。事實上，Hill估計方法沒有利用到匯率收益序列的GARCH結(jié)構(gòu)。Hill方法的具體估計值方法是，首先寫出收益率序列γt的順序統(tǒng)計量：

t1，T≥γ2，T≥L≥γT，T，其中T為樣本容量，則由Hill方法給出的尾指數(shù)的估計值為：其中m＝m（T）滿足若序列γt是i． i．d的且參數(shù)由此給出的κ1＞0，則估計值是穩(wěn)定的、漸近正態(tài)的，即：作為尾指數(shù)κ1的一個估計滿足：

Hill（2010）證明了在經(jīng)典的GARCH（1，1）模型下，上述

記Starica和Pictet（1997）［13］給出的替代Hill估計的新估計為。Mikosch和Starica（2000）給出了在GARCH（1，1）結(jié)構(gòu)下尾指數(shù)應(yīng)滿足的條件。Berkes等（2003）證明了在GARCH（1，1）結(jié)構(gòu)下新估計的漸近正態(tài)性定理，Iglesias和Linton（2009）又將此估計推廣值由Glosten等（1993）構(gòu)造的GJR—GARCH模型。下面介紹基于GARCH模型類的尾指數(shù)估計的新方法。Breiman（1965）給出一個在處理混合分布尾部時非常有用的結(jié)論，具體如下：

定理1［15］設(shè)X＝Y(jié)Z，其中Y是非負隨機變量且與隨機變量Z獨立，若：

Y有正則變化的尾部，記其尾指數(shù)為α，存在ε＞0，使得E（Zα＋ε＜∞，

那么X有規(guī)則變化的尾部，其尾指數(shù)也是α，且有：

P（X＞x）∶E（Zα）P（Y＞x），x→∞成立。

Mikosch和Starica（2000）分析了GARCH（1，1）模型 （見 （1a）（2b）），他們得出在擾動εt弱相依的條件下，序列γt有規(guī)則變化的尾部，若記其尾指數(shù)為κ，則κ滿足方程

由尾指數(shù)κ所應(yīng)滿足的方程，通過模擬可以發(fā)現(xiàn)，當假定擾動項服從的分布尾部越重則GARCH模型的尾部也會更重，當在模型中減少ARCH效應(yīng)（即α減小）增加GARCH效應(yīng)（即β增大）時模型的尾部會減輕。

Mikosch和Starica具體的給出了新估計的方法，他們證明存在一個正常數(shù)c0和尾指數(shù)κ參數(shù)，使得：

為了估計尾指數(shù)參數(shù)κ，首先給出GARCH（1，1）模型中參數(shù)（ω，α，β）的一個估計如最大似然估計則新方法下κ的估計值是方程的解。

該估計被Iglesias和Linton（2009）推廣到GJR—GARCH模型中，并利用漸近正態(tài)分布理論得到了Hausman檢驗：在經(jīng)典的GARCH（1，1）模型下有成立。

1．3 風險值（VaR）的計算方法

我們利用由上述兩種方法估計出的尾指數(shù)計算外匯市場的匯率收益的VaR值。Iglesias和Linton（2009）給出對于比較小的α，風險值VaR滿足等式α＝Pr［yt＞VαRα］＝c0VαRα－κ，從而風險值可以由下面公式給出VαRα＝（c0／α）1／κ，下面給出c0的估計值。

Iglesias和Linton（2009）指出上述可以由以下式子給出估計：

從而VαRα的估計值為：

接下來如果我們使用Hill估計，則對應(yīng)的估計值為：

2 實證分析

我們使用的數(shù)據(jù)是外匯市場4種貨幣：美元、港幣、日元和歐元對人民幣匯率的日收益率，取樣時間為2006年1月4日至2013年11月5日，借鑒Payaslioglu（2009）和Iglesias（2012），本文考慮的收益率是對數(shù)收益率，即rt＝log（Pt／Pt－1），其中t＝1，2，L，T。

首先利用ADF（1979）檢驗對收益率序列進行了單位根檢驗，拒絕了有單位根的原假設(shè)，接受序列是平穩(wěn)的。圖1是4種貨幣對人民幣日收益率圖，表1給出了它們一些基本統(tǒng)計量，可以據(jù)此初步得出4個序列都存在尖峰厚尾現(xiàn)像、條件異方差以及波動率集聚現(xiàn)象，從而我們選擇采用GARCH類模型進行建模。

其次我們利用Hill方法估計了4種貨幣匯率收益率序列的尾指數(shù)κ的值，結(jié)果由表3給出。

接著采用Iglesias和Linton（2009）的新方法估計了4種貨幣匯率收益率序列的尾指數(shù)κ的值。在建立GJR—GARCH模型前，通過檢驗對數(shù)收益率序列的標準化后的殘差序列rt／σt及其平方的自相關(guān)圖和偏相關(guān)圖，發(fā)現(xiàn)標準化后的殘差平方序列存在顯著的自相關(guān)性，也就說明了序列存在高階ARCH效應(yīng)，故需要采用GARCH類模型進行建模。經(jīng)過多次試驗，并通過AIC準則進行對比，發(fā)現(xiàn)GJR—GARCH（1，1）模型（見（3a）和（4b））最為合理，在表2中我們給出了該模型各參數(shù)的最大似然估計值。通過對上述模型的殘差序列進行條件異方差的ARCH LM檢驗和觀察殘差平方的自相關(guān)和偏相關(guān)圖，都可以發(fā)現(xiàn)利用GJR—GARCH模型消除了原殘差序列的ARCH效應(yīng)，模型可以使用。隨后由（8）給出了新方法估計出的尾指數(shù)，見表3。

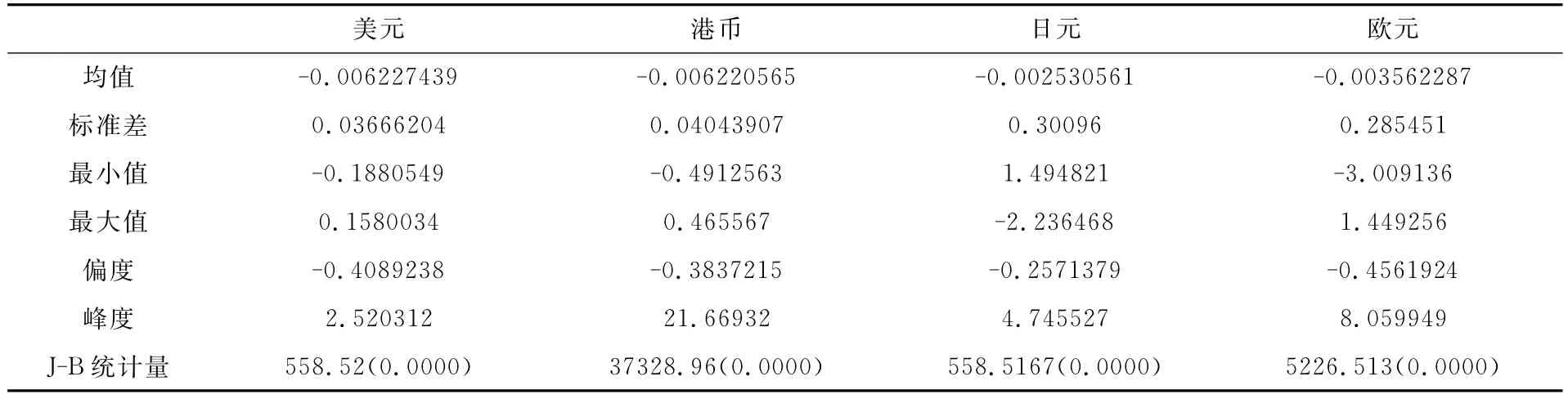
表1 各種貨幣對人民幣匯率對數(shù)日收益率數(shù)據(jù)統(tǒng)計特征

表2 GJR—GARCH模型各參數(shù)估計值

最后我們利用公式（10），（11），（12）和（13），在水平下，我們計算出了的各種貨幣對人民幣匯率日收益率的VaR，詳見表3。

表3 尾指數(shù)及VaR的估計值（α＝0．001）

對于港幣來說，我們發(fā)現(xiàn)新方法的估計值在統(tǒng)計意義上幾乎為零，這是因為如果數(shù)據(jù)和模型不匹配，那么 （5）式不一定有解。然而，對于日元新方法估計的尾指數(shù)等于2．20，通過觀察Hausman統(tǒng)計量值（見（9）式），我們發(fā)現(xiàn)采用新方法估計日元對人民幣匯率收益率序列的尾指數(shù)時，Huasman統(tǒng)計量通過了檢驗，這樣可以從理論上說明應(yīng)用新方法對日元匯率的風險進行預測是可行的；而且通過與Hill估計得到的VaR進行比較發(fā)現(xiàn)使用新方法預測的VaR要小很多，從節(jié)約投資成本、提高資本利用效率的角度來看，應(yīng)用這樣一種無偏的估計無疑對于預測日元匯率市場來說更加具有優(yōu)勢。同樣的道理，就美元和歐元而言，由Hausman類型的檢驗結(jié)果可知，使用Hill估計法更合適。

綜上所述，對于日元來說，我們更傾向于使用 （11）式而不是 （13）式來計算日元匯率風險值。那么，對于余下的三種貨幣來說，式 （13）是優(yōu)于式 （11）的。此外，表3也列出了各種貨幣匯率的VaR在兩種不同方法下的估計值 （取α＝0．001）。

3 結(jié)論

從實證分析的結(jié)果可以看出，對于不同貨幣的匯率日收益率，結(jié)果表明基于Hill（1975，2010）估計尾指數(shù)方法得到的四種外匯匯率序列的尾指數(shù)差異不大，由Hill方法估計出來的VaR表明，四種貨幣中日元存在的風險最大，而美元存在的風險最小，這樣為投資者和投資機構(gòu)在進行投資時如何通過選擇合適外匯投資組合降低市場風險提供一定的建議。但使用Iglesias和Linton的新方法估計的結(jié)果是日元的風險值最小，若根據(jù)該方法預測的風險值進行配置風險保證金，有利于提高投資機構(gòu)的資金使用率，且該方法通過了Hausman類型的檢驗，故我們更傾向于使用新方法對日元的匯率進行研究。對于日元而言，Hill估計法也許高估了它的風險值。通過對估計出VaR進行比較也可以看出，相對于Hill估計，對于美元、港幣和歐元在新估計方法下得到的風險值更大些，過大的估計了潛在的極端風險。而對于日元，采用Hill估計對以人民幣為基準的外匯匯率的風險進行估計時，會高估潛在的極端風險。綜合以上可以看出，在進行市場風險管理時，采用一些不同的方法進行預測估計風險值，再通過對不同方法得到的預測值比較檢驗，最終選擇一個合適的風險值進行風險保證金配置，從而達到在有效控制風險的前提下提高資本的利用效率，以提高投資者和投資機構(gòu)的收益。

［1］ Wagner，N．a(chǎn)nd Marsh，T．A．Measuring tail thickness under GARCH and an application to extreme exchange rate changes［J］．Journal of Empirical Finance，2005，（12）：165－85．

［2］ Hill，J．B．On tail index estimation for dependent heterogeneous data［J］．Econometric Theory，2010（26）：1398–436．

［3］ Hill，B．M．A simple general approach to inference about the tail of a distribution［J］．Annals of Statistics，1975，（3）：1163－74．

［4］ Mikosch，T．a(chǎn)nd Starica，C．Limit theory for the sample autocorrelations and extremes of a GARCH（1，1）process［J］．Annals of Statistics，2000，（28）：1427－51．

［5］ Payasliog lu，C．A tail index tour across foreign ex－change rate regimes in Turkey［J］．Applied Economics，2009，（41）：381－97．

［6］ Iglesias Emma M．，An analysis of extreme movements of exchange rates of the main currencies traded in the Foreign Exchange market［J］．Applied E－conomics，2012，（44）：4631－4637．

［7］ 邵騰偉，冉光和．基于POT－GPD損失分布的農(nóng)業(yè)自然災害VAR估算［J］．統(tǒng)計研究，2011，（28）：79–83．

［8］ 茍紅軍，陳迅，花擁軍．基于GARCH－EVT－COPULA模型的外匯投資組合風險度量研究［J］．管理工程學報，2015，（1）：183－189．

［9］ Yia，Y．，F(xiàn)eng X．，Huang Z．，Estimation of extreme value－at－risk：An EVT approach for quantile GARCH model［J］．Economics Letters，2014，（3）：378－381．

［10］ Bollerslev，T．．Generalized autoregressive conditional heteroskedasticity［J］．Journal of Econometrics，1986，（31）：307－327．

［11］ Glosten，L．R．，Jagannathan，R．，Runkle，D．E．，On the relationship between the expected value and the volatility of the nominal excess returns on stocks［J］．Journal of Finance，1993，（48）：1779–801．

［12］ Leadbetter，M．R．，Extrems and local dependence in stationary sequences［J］．Zeitschriftfur Wahrscheinlichkeitsthorie und Verwandte Gebiete，1983，（65）：291－306．

［13］ Starica，C．，Pictet，O．The tales the tails of GARCH processes tell［M］．Unpublished Working Paper，1997．

［14］ Breiman，L．On some limit theorems similar to the arc－sin law，Theory of Probability and Its Applications，1965，（10）：323－331．

［16］ 陳堅．中國股票市場尾部風險與收益率預測——基于Copula與極值理論的VaR對比研究［J］．廈門大學學報：哲學社會科學版，2014，（4）：45－54．

責任編輯：陸廣品

Measuring Value at Risk of Foreign Exchange Rate Based on Tail Index－Taking USD，HKD，JPY and EUR against RMB for Example

PAN Xue－yan1，2，CAI Guang－h(huán)ui1，LIU Shun－Xiang1（1．School of Statistics and Mathematics，Zhejiang Gongshang University，Hangzhou310018；2．School of Mathematics and Computer Science，Anhui Normal University，Wuhu Anhui 241003，China）

exchange rate；VaR；EVT；GARCH－type models；tail index

With the extreme value theory with the GARCH－type models and the new method of tail index estimation given by Iglesias as well as the estimation method given by Hill，analyze the day logarithm yield sequence of the exchange rate of USD，HKD，JPY and EUR against RMB from January 4，2006to November 5，2013respectively and estimates their VaR by different methods．The results show that，for the JPY，the VaR based on the new method of tail index estimation is more appropriate than that based on the method of Hill estimation，but it is opposite for the USD，HKD and EUR．

C812

A

1001－2435（2015）05－0558－06

10．14182／j．cnki．j．a(chǎn)nu．2015．05．004

2014－11－06；

2015－06－11

國家自然科學基金項目（11101364，11201421）；浙江省自然科學基金項目（Y6110110）；全國統(tǒng)計科研計劃項目（2013LY137）和浙江省高校人文社科重點研究基地（統(tǒng)計學）資助。

潘雪艷（1981－），女，安徽桐城人，博士研究生，講師，研究方向：金融風險管理、金融統(tǒng)計、金融數(shù)據(jù)分析建模；蔡光輝（1978－），男，浙江人，教授，博士生導師，研究方向：金融風險管理、金融統(tǒng)計、金融數(shù)據(jù)分析建模；劉順祥（1989－），男，江蘇鎮(zhèn)江人，碩士研究生，研究方向：金融風險管理。