基于優化頂點彈簧模型的半沉浸環境標定算法

楊廷俊，朱 博，劉 雨

（1.浙江大學 計算機科學與技術學院，浙江 杭州310027；2.浙江大學 航空航天學院，浙江 杭州310027）

沉浸式可視化系統通常被設計為應用虛擬現實技術來模擬真實世界中的各種真實感體驗，用戶在不需要佩戴任何頭戴顯示器或其他輔助設備的情形下，便可以在虛擬環境里自由地漫游［1-2］.球幕投影系統作為沉浸式曲面可視化系統代表，通過將觀察者包圍在減少了邊緣干擾的球形屏幕之中，同時對環繞觀察者周圍的視場進行圖像預先扭曲，從而提供了一個具有強烈真實感的可視化環境.早期球幕投影系統的使用場景僅僅局限于天文館，他們使用多臺專門投影硬件，將星空圖像和其他類型多媒體資料在球形幕布上投影，進行天文學知識的公共教育領域.隨著DLP（digital light procession）投影技術在大型天文館的廣泛應用，通過小型球幕投影系統可以獲取昂貴的專業星象球機設備同樣的視覺體驗，得到了越來越多的關注.小型球幕系統硬件一般由單臺商用數字投影機配備普通魚眼鏡頭構成，球幕直徑常介于2～5m，因而可以在很多場所方便地進行配置.與傳統多臺投影機構成天文館系統相比，不需要任何特殊硬件裝置，也不需要專門圖像融合軟件進行拼接，非常適合在科學可視化、模擬仿真環境等場景中進行使用.

對于現有的投影可視化系統，由于投影表面形狀和投影機安裝位置等因素，圖像在投影到投影表面時常會出現扭曲現象，幾何標定是通過對該扭曲參數進行估計，實現對投影圖像的預先校正工作［3］.目前，大多數投影系統都廣泛采用基于相機反饋輔助的標定算法，將平面屏幕系統中的該問題轉換為相機和投影機之間單向性矩陣的計算［4-6］.對于曲面和非平面屏幕系統，幾何標定不能由單一的單線性矩陣描述，Raskar等［7-9］使用一對正交的立體照相機，并通過保角映射和二次傳遞的方法來進行標定，該方法僅適用于標準二次曲面.Majumder等［10-12］使用單臺相機并通過有理貝塞爾面片的方法對CAVE和球幕系統進行幾何標定；該方法要求投影表面為標準球幕表面，并需要在投影表面放置物理的校正標記.

針對現有曲面投影環境標定算法在自適應校正精度和計算效率上的不足，本文提出一種基于優化頂點彈簧模型的半沉浸式投影環境快速自適應標定算法.首先基于優化的頂點彈簧模型對非均勻二次曲面進行三維網格獲取；然后，使用曲面細分方法根據人眼視線與網格面片的空間幾何關系，對網格進行進一步的網格細分計算；最終根據細分結果，網格對投影圖像進行精確預校正，實現半沉浸式投影環境的快速自適應標定.

1 基于球幕的半沉浸可視化系統建模

1.1 非均勻二次球形曲面數學模型

基于球形幕布投影的半沉浸式可視化環境需要應用非均勻曲面網格的精確計算.為了分析球面投影圖像的變形情況需要建立非均勻二次球面投影模型，可以將球面屏幕簡化為一個球面，投影機的投影光線簡化為一個四棱錐體.如圖1所示，投影機的投影位置在z軸上的P 點，投影機的投影方向通過球心O，則投影機的投影光束呈一個四棱錐形，它與球面相交，在球面上生成一個比較規則的準矩形曲面，即投影光束所形成的四棱錐體為P-Q1Q2Q3Q4.

假設球體的半徑為R，則球面上的坐標點（x，y，z）可以用參數化的經緯坐標（θ，φ）表示為

為了簡化投影光束的表達，將投影機投影光束的邊界表示為4 個平面，采用4 個方程來表示.PQ1Q2、PQ3Q4、PQ2Q4和PQ4Q1平 面 的 表 達 式分別為

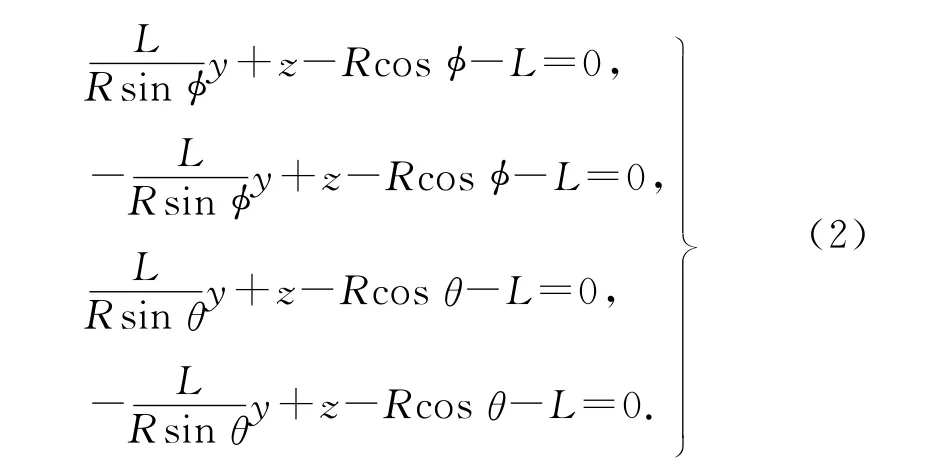
式中：L 為投影機與球面的成像距離.

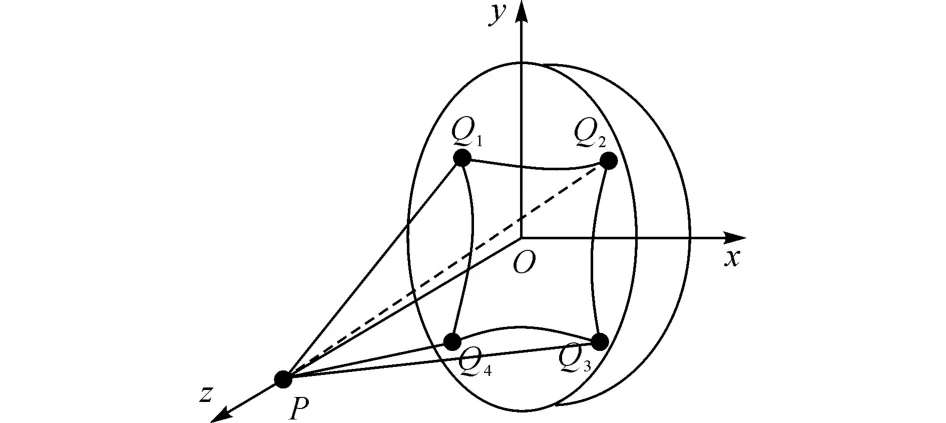
圖1 球形曲面投影模型Fig.1 Spherical projection model

1.2 魚眼光學系統

本文設計的球幕投影系統使用加裝魚眼鏡頭的方式組成投影光學系統進行投影成像（見圖2（a））.魚眼鏡頭成像的球面投影模型（見圖2（b）），其定義為從原點O 指向空間任一點A（x，y，z）的射線斜交投影球面于一點.將這一點正投影到一個與z 軸垂直的固定平面上（由于該平面上各點的z 坐標相同，只考慮x 和y 坐標），得到平面點B（m，n）.空間各點A（x，y，z）在所給固定平面上的投影B（m，n）即構成魚眼鏡頭成像，利用該模型的逆變換可以將魚眼鏡頭圖像變換為透視投影圖像.

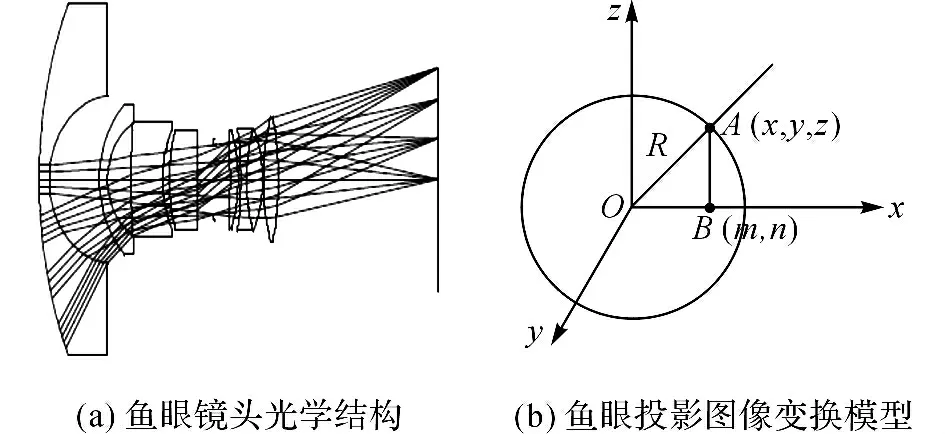
圖2 魚眼鏡頭投影系統Fig.2 Fisheye lens projection system

利用魚眼鏡頭可以得到180°高匯聚和大視角的圓形魚眼圖像，反之180°圓形魚眼圖像的大視角和高匯聚性通過180°魚眼投影鏡頭從投影到球面便能將景深部分信息還原（見圖3）.這種魚眼投影配合球形曲面投影系統給人造成的視覺誤差，能夠讓人產生如臨現場的沉浸感.

圖3 魚眼鏡頭投影示例Fig.3 Fisheye lens projection example

2 基于優化頂點彈簧模型的自適應快速標定算法

2.1 頂點彈簧網格變形方法

頂點彈簧模型（vertex springs model）是非結構動網格彈簧近似法的一種.假設將網格單元的各條邊看作彈簧，則彈簧系數與網格邊的長度有關.當網格邊界發生自適應移動后，通過求解彈簧系統節點受力平衡確定網格點的新位置.該非結構動網格變形方法通過網格變形、網格重構和局部網格重構等方法使計算網格適應計算區域的改變，是一種非定常問題數值模擬的關鍵技術，可以應用于可變形飛行器、機翼氣動彈性振動、生物仿生流等問題所涉及的非定常問題求解.

本文研究的基于球形幕布投影的半沉浸式可視化環境需要進行非均勻曲面網格的精確計算，應用非結構動網格變形方法可以在保持網格數目不變的情況下，通過網格結構變形來適應運動邊界引起的物理空間變化.變形動網格可以針對球幕曲面環境的物理性質，建立有效控制網格變形和運動的計算模型.基于頂點彈簧模型的非結構網格具有幾何上的靈活性，易于處理復雜曲面形狀模型，同時網格生成的自動化程度高.球幕的有效投影環境邊界獲取之后，在計算網格區域內可以自動生成網格，當網格邊界發生改變時，運動邊界帶動有效網格區域內的網格節點運動，依靠網格邊的伸縮、扭轉來適應邊界的運動.

基于頂點彈簧模型的網格變形計算如圖4 所示，其中圖4（a）所示為非結構網格的示例圖.彈簧法假設網格節點由彈簧連接，整個計算域網格是一個達到平衡狀態的彈簧系統.

如圖4（b）所示為非結構網格局部放大的頂點彈簧模型示例圖，網格邊可以看作彈簧連接，連同節點i、j間的組成頂點彈簧變形模型.獲得由于邊界變形或運動帶來的網格節點位移，從而得到適應計算域變化的計算網格.其中將網格邊看作彈簧，節點i、j之間的彈簧張力計算為

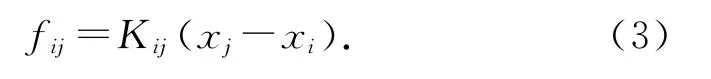
式中：Kij為彈簧的倔強系數，xi、xj分別為節點i、j的位置矢量.節點i所受的合力如式（4）所示，其中Ni為與節點i相連的相鄰節點總數.

在初始網格確定后，使用式（4）得到節點i的初始狀態，則運動邊界上的點移動后，可以構造線性方程得到其他網格點的新位置坐標：

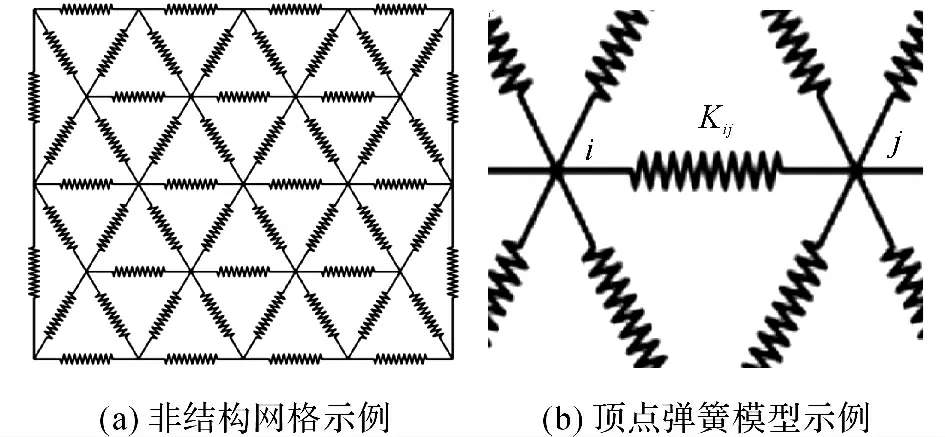
圖4 頂點彈簧模型Fig.4 Vertex springs model

式中：下標npsum 為運動邊界點數量.分析上述線性方程，由于對角線元素求和指標j取遍該行所有非對角線不為0的列k，因此該方程對角占優，采用Jacobi迭代格式收斂如下公式：

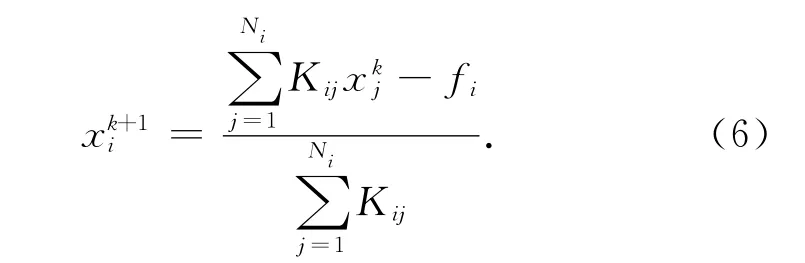
2.2 基于優化頂點彈簧模型的球幕網格計算

如圖5（a）所示為球幕網格示例，將最外圍的球幕網格邊緣作為網格變形邊界，根據實際球幕的物理幾何形狀來不斷地變化邊界節點.從圖5（b）可以看出，網格節點之間的連接是不等長線段，需要求解圖4（b）中的球幕網格的彈簧倔強系數Kij.

根據頂點彈簧模型（式（7）），可以將彈簧倔強系數設置為常數，網格點以東后的新位置坐標可以通過周圍點坐標的雙線性插值計算得到.常用的彈簧倔強系數計算與網格節點之間的距離成倒數，對于球幕網格可以應用二維頂點彈簧倔強系數計算公式：

式中：lij為節點i、j之間的距離.當網格不斷壓縮變形時，倔強系數不斷增大，保證球幕網格節點之間保持一定的間距.在實際計算過程中會出現如圖6所示不可預知的“網格拆穿”（mesh snap-through），根據頂點彈簧模型在整體球幕網格的作用力，這種牽引作用距離邊界越遠影響越小，最早發生網格變形失敗的網格單元一般位于網格邊緣附近.

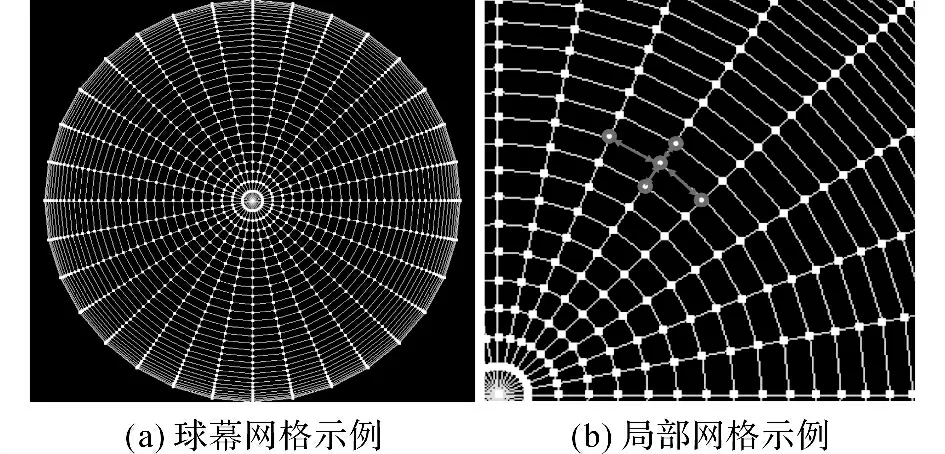
圖5 球幕網格示例圖Fig.5 Dome mesh example

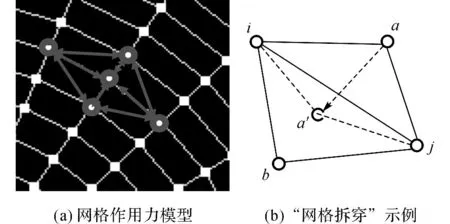
圖6 頂點彈簧模型的“網格拆穿”Fig.6 “Mesh snap-through”in vertex springs model

為了解決上述網格拆穿情況，對經典頂點彈簧倔強系數計算方法進行改進，優化的倔強系數計算方法綜合考慮網格的伸縮和扭轉作用，引入網格變形修正因子S1和S2.其中，S1是一個與網格邊界相關的空間位置函數，可以通過橢圓方程計算得到，由于球幕網格的特殊形狀，可以設置為一個常數.S2是二維網格扭轉因子，可以由下式計算得到：

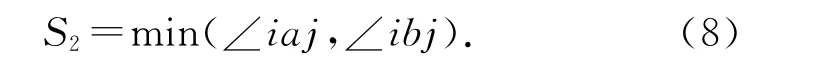
最終優化的適用于球幕網格的頂點彈簧倔強系數計算公式如下：

隨著網格節點之間的距離和夾角變化，lij和S2不斷變化，倔強系數需要實時更新.

在實際計算中，彈簧網格中的實時受力狀況與初始受力相同，則第i個節點在網格彈簧系統中所受的合力僅需計算一次，在計算過程中保持不變.對于優化的彈簧倔強系數需要按照一定的頻率刷新，可以迭代100步以上更新一次，基于以上算法實現的球幕網格計算步驟具體如下.

1）使用“投影機-相機”系統獲取球幕環境的采集圖像，應用Sobel分割算法和圖像二值化算法提取球幕邊緣，得到球幕邊緣坐標集合.

2）繪制原始球幕網格圖形作為初始網格，通過式（9）計算得到優化后的初始倔強系數，最終構造頂點彈簧模型.

3）結合步驟1）計算得到的球幕邊緣坐標，使用頂點彈簧模型建立網格彈簧系統方程，得到網格內所有節點的新坐標集合.

4）通過“投影機-相機”系統進行球幕網格校正圖像反饋，多步迭代計算節點坐標并更新.

5）通過步驟3）建立的線性方程迭代收斂，并實時使用4）的實時在線閉環系統進行校正結果反饋，最終校正球幕網格.

2.3 基于曲面細分算法和GPU 加速的球幕校正投影圖形渲染

由于在魚眼鏡頭的投影模式下，球幕幾何網格中任意一條邊上的2個頂點之間，其距離并非原始投影之前的直線關系，而是經過魚眼透視的空間曲線；對于球幕投影中人眼觀察到的球幕表面區域，為了提高魚眼投影校正的精度，四邊形網格需要被進一步細化.從OpenGL 4.0［13］標準以及DirectX 11.0［14］開始，基于硬件的參數表面曲面細分技術便被引入了新一代顯卡的可編程圖形流水線中.

本文的研究工作均使用OpenGL來實現，因此接下來的內容均只介紹OpenGL中的實現方法.在加入了曲面細分的硬件支持之后，目前OpenGL 4.0以上標準中的GPU 的繪制流水線如圖7 所示.在該繪制流水線中，硬件曲面細分工作包含了圖中藍色的3個單元：細分控制著色器（TCS）、細分圖元產生器（TGP）和細分評估著色器（TES）.TCS根據細分參數對片元的屬性及內部的頂點屬性進行修改；TGP單元根據下一單元TES的輸入數據格式，將對TCS傳入的片元內部的頂點進行分割；TES 將TGP分割后每個頂點的局部坐標變換成世界坐標，并對頂點的相應屬性進行轉換.

在球幕投影系統中，為了減少更精細網格數據的存儲和CPU（中央處理器）／GPU 的總線開銷，利用顯卡中的獨立功能硬件進行曲面細分.根據網格面片與人眼視線方向的夾角作為參數描述，在需要細分網格的區域生成密集的三角化面片：網格面片與人眼視線方向的夾角越小，人眼對于魚眼投影失真的容忍度越小，網格曲面需要細分的精度越大；網格與視線的夾角越大，人眼對于其繪制效果的敏感度越低，網格細分的精度越小.細分參數的計算如下：

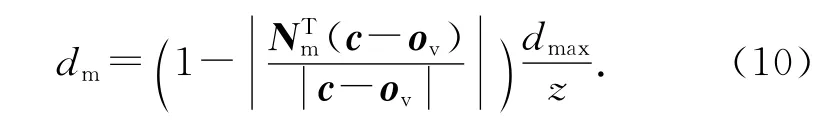
式中：dm為單個網格的細分參數，Nm為網格面片的歸一化法向向量，dmax為細分參數的最大值，z 為人離球幕的距離，c為人眼所在的位置，ov為人眼視線與球幕交點的位置.

對于網格細分算法，為了更好地利用以上的曲面細分繪制流水線，減少網格數據的復雜度，并避免細分算法的迭代情況出現，選擇PN（Point-Normal）三角細分算法.PN 三角細分法是Vlachos等［15］提出的一種基于三角化網格的曲面細分方法，它通過一種特殊的貝塞爾曲面來替換原始的三角網格.對于任意的三角面片，輸入頂點Vi＝（Pi，Ni），其中Pi為頂點位置，Ni為頂點對應的法線向量；新頂點的重心坐標u、v、w∈R3，該細分法產生的細分曲面可以表示為

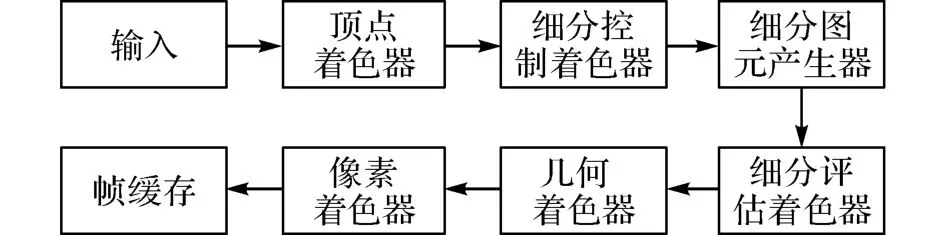
圖7 基于曲面細分算法的GPU 圖形繪制流水線Fig.7 Graphics pipeline for hardware tessellation

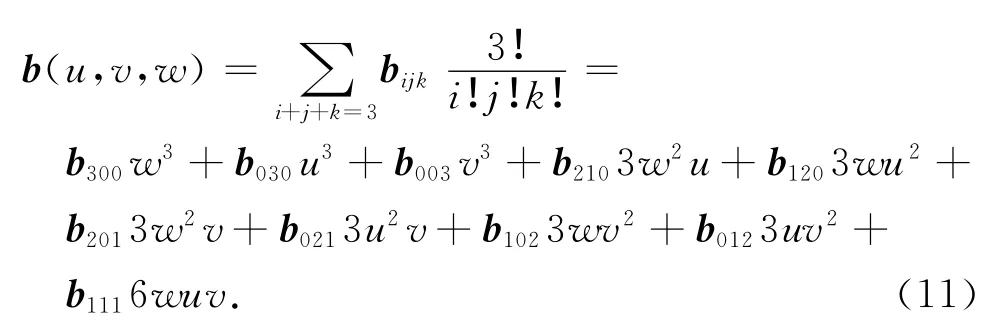
式中：u ＋v ＋w ＝1；bijk為PN 三角片的控制點，如圖8所示，計算公式如下：

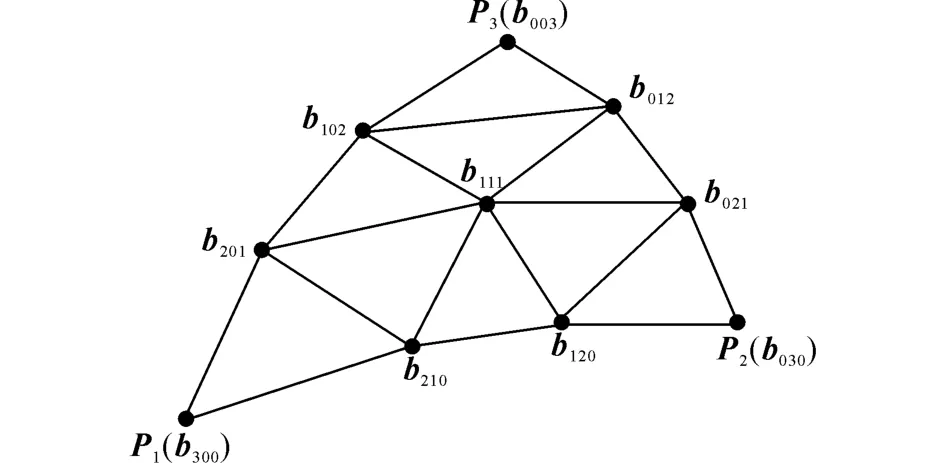
圖8 PN 三角細分法Fig.8 Curved PN triangles

為了減少基于視點的曲面細分過程中，頻繁使用曲面細分帶來的額外計算負荷，本文利用了OpenGL 4.0新流水線下的另一新特性：Transform Feedback技術［16］.所謂Transform Feedback，即對當前在GPU 流水線上的頂點數據，在經過頂點處理和曲面細分等處理后，進入到光柵化步驟之前，將之前流水線處理的結果數據，保存到緩存結構中.在本文的球幕網格校正系統中，基于Transform Feedback使用了Two-Pass的繪制策略：當用戶視點發生改變時，進行一次曲面細分，并將細分結果保存在顯卡內存中，并在下一次用戶視點變化之前，一直使用之前曲面細分的結果網格，進行球幕圖像的繪制；當用戶視點再次改變時，根據新的視線方向，對初始的稀疏網格進行再一次的細分，從而減少重復的頂點數據處理和增加繪制性能.

3 算法實現和驗證

為了評估基于優化頂點彈簧模型的快速自適應標定算法效果，搭建了單臺投影機組成的小型球幕實驗環境：幕布采用直徑為2m 的一體成型半球型無縫正投球幕；投影機使用物理分辨率為1 920×1 080的DLP投影機；魚眼鏡頭采用基于等距投影映射模式的Peleng 8mm f／3.5鏡頭；相機使用羅技QuickCam Pro 9000型號攝像頭；標定計算的電腦顯卡使用Nvidia GTX 750，其支持CUDA（Compute Unified Device Architecture）技術和OpenGL 4.0標準.如圖9所示為本文提出的基于優化頂點彈簧模型的快速自適應標定算法實現和驗證實驗.

圖9（b）展示了整個實驗的硬件環境，其中，魚眼鏡頭與投影機鏡頭位于同一光軸線上，由于從魚眼鏡頭出射的光線能夠覆蓋180°的視場，整個投影球幕都位于覆蓋范圍之內.根據該標定算法的計算步驟可知，整個標定的過程如下.

1）使用相機獲取球幕環境的采集圖像，利用圖像分割算法得到球幕邊緣.

2）繪制原始球幕網格圖形作為初始網格，并構造頂點彈簧模型，圖9（b）展示了初始網格的投影效果.

3）通過“投影機-相機”系統和球幕邊緣的位置信息，進行球幕網格的彈簧模型迭代更新，圖9（c）展示了通過多次迭代計算的最終效果.

4）利用GPU 圖形硬件的曲面細分功能，根據網格面片與人眼視線的關系，進行自適應的網格細分，圖9（d）展示了經過曲面細分后的網格結果.

將標定結果應用到球幕投影的圖像渲染，如圖9（e）、（f）分別為圖片播放和模擬飛行的效果圖.

為了驗證本文提出的快速自適應標定算法的校正精度和效率，使用幾種現有的主流球幕投影系統校正方法［17-18］進行實驗比較，算法的比較結果如表1所示.

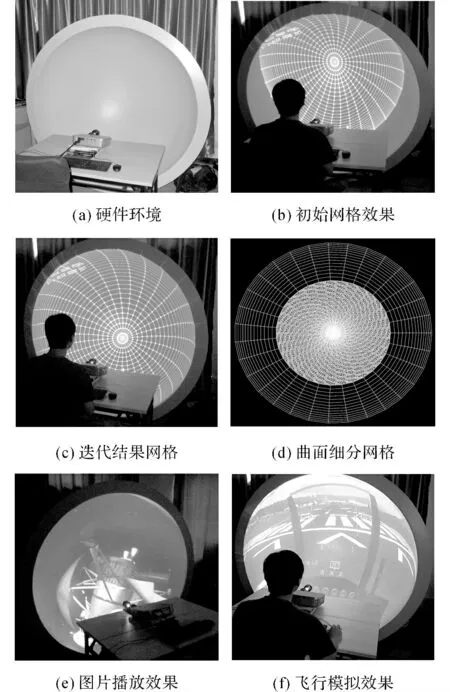
圖9 本文提出的標定算法實現和驗證實驗Fig.9 Implementation and experimental validation of proposed calibration algorithm

表1 算法實驗比較結果Tab.1 Comparison of results

與激光網格標定方法和有理貝塞爾曲面標定算法這2種現有主流的球幕標定方法相比，使用本文提出的基于優化頂點彈簧模型的球幕標定算法可以從3個方面體現出明顯優勢.1）在投影模式上，由于多投影機拼接系統不僅需要多臺高流明的工業投影機，還需要額外圖形融合硬件進行多通道融合工作；使用單投影機投影在工程造價上遠小于多投影機拼接方法，可以大大降低球幕投影設備的硬件成本.2）在校正精度上，由于多投影機拼接本身的復雜性以及投影機光學投影硬件本身的關系，不同投影機很可能出現顏色空間和亮度空間不統一的現象，相鄰投影機投影區域之間的裂縫和顏色跳變，很容易造成視覺感知的敏感；本文提出的單投影機標定算法不僅可以達到低于0.5像素的校正精度，小于等于原有多投影機標定算法中的最高校正精度，并且由于單投影機的色彩分布更加均勻，能夠給用戶提供更好的視覺體驗.3）在校正效率上，多投影機拼接系統需要水平儀或其他輔助設備進行精密測量，同時需要投入具有深厚工程經驗的技術人員進行操作校正軟件，不僅降低了系統的易用性，而且加大了整個校正過程的時間；本文提出的基于優化頂點彈簧模型的算法，整體標定時間小于3min，低于原有方法中至少5min的校正時間需求.

4 結 語

本文針對半沉浸式投影環境的標定計算提出一種基于優化頂點彈簧模型的自適應快速校正算法.該算法基于球幕投影過程中由于鏡頭光線傳輸和曲面投影表面引起的扭曲現象，借助“投影機-相機”構成的光學反饋系統，通過對彈簧模型的不斷迭代和更新工作，能夠快速、方便地完成整個球幕的粗粒度校正操作；然后對人眼視線對應的需要高精度網格的敏感區域，通過基于圖形硬件加速的曲面細分技術，結合PN 三角面片細分方法，使用更加精細的貝塞爾曲面來對投影曲面進行細分模擬.

算法驗證和比較實驗結果表明，使用本文提出的基于優化頂點彈簧模型的自適應快速標定方法可以顯著地加速球幕投影系統的整體校正效率，同時大幅提升投影圖像的校正精度，并且在降低球幕投影系統硬件成本的同時得到了符合視覺檢驗的投影圖像校正效果.下一階段的工作將集中在全沉浸式球幕標定方法以及基于球幕投影系統的虛擬現實技術的研究2個方面，希望在未來的工作中逐步完善球幕投影系統的應用，為沉浸式虛擬現實環境提供一種新型的可視化技術.

（

）：

［1］DEFANTI T A，SANDIN D J，CRUZ-NEIRA C.A“room”with a “view”［J］.IEEE Spectrum，1993，30（10）：30-33.

［2］CRUZ-NEIRA C，SANDIN D J，DEFANTI T A，et al.The CAVE audio visual experience automatic virtual environment［J］.Communnications of the ACM，1992，35（6）：64-72.

［3］HARVILLE M，CULBERTSON B，SOBEL I，et al.Practical methods for geometric and photometric correction of tiled projector displays on curved surfaces［C］∥Proceedings of CVPRW.New York：IEEE，2006：52-59.

［4］BROWN M，MAJUMDER A，YANG R.Camera-based calibration techniques for seamless multi-projector displays［J］.IEEE Transactions on Visualization and Computer Graphics，2005，11（2）：193-206.

［5］SUKTHANKAR R，STOCKTON R G，MULLIN M D.Smarter presentations：exploiting homography in camera-projector systems［C］∥Proceddings of the 8th International Conference on Computer Vision （ICCV-01）.Vancouver：IEEE，2001：247-253.

［6］OKATANI T，DEGUCHI K.Autocalibration of a projector-camera system［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（12）：1845-1855.

［7］RASKAR R，BAAR J，RAO S，et al.Multi-projector imagery on curved surfaces［R］.Cambridge：Mitsubishi Electric Research Labs，2004.

［8］BAAR J，RASKAR R.Flexible calibration of multiple projectors for low-cost curved screen displays ［C］∥Proceddings of 14th International Conference on Artificial Reality Telexistence.Seoul：［s.n.］，2004：263-268.

［9］RASKAR R，BAAR J，WILLARCHER T，et al.Quadric transfer for immersive curved screen displays［J］.Computer Graphics Forum，2004，23（3）：451-460.

［10］SAJADI B，MAJUMDER A.Automatic registration of multiple projectors on swept surfaces［C］∥Proceddings of 17th ACM Symposium on Virtual Reality Software and Technology. Hong Kong：ACM，2010：159-166.

［11］SAJADI B，MAJUMDER A.Auto-calibration of multi-projector CAVE-like immersive environments［J］.IEEE Transaction on Visualization and Computer Graphics，2012，18（3）：381-393.

［12］SAJADI B，MAJUMDER A.Automatic registration of multi-projector domes using a single uncalibrated camera［J］.Compututer Graphics Forum，2011，30（3）：1161-1170.

［13］SEGAL M，AKELEY K.OpenGL 4.0specification［M］.［S.l.］：Khronos Group Inc，2010.

［14］SHERROD A，JONES W.Beginning DirectX 11game programming［M］.Boston：Cengage Learning，2011.

［15］VLACHOS A，PETERS J，BOYD C，et al.Curved PN triangles［C］∥Proceedings of the 2001Symposium on Interactive 3D Graphics.New York：ACM，2001：159-166.

［16］ROST R，LICEA-KANE B.OpenGL shading language［M］.3rd ed.Boston：Wesley，2010.

［17］李賽.面向大型遺址的球幕展示系統研究與實現［D］.杭州：浙江大學，2012.LI Sai.Dome display systems research and implementation for large sites［D］.Hangzhou：Zhejiang University，2012.

［18］梁思毓.面向球幕的編輯式多投影校正技術與系統［D］.上海：復旦大學，2012.LIANG Si-yu.Multiple projection calibration technology based on interactive editing for dome systems［D］.Shanghai：Fudan University，2012.