結構可靠度分析中的混合模擬法及應用

蔣正文，萬 水，李明鴻，馬 磊

（東南大學 交通學院，江蘇 南京210096）

對實際工程進行結構可靠度分析，可以發現大部分結構具有隨機變量多、隱式功能函數等特點［1］.針對顯式結構功能函數的數值積分法、改進一次二階矩法［2］等傳統方法顯然難以解決以上問題.Monte-Carlo法在處理隱式功能函數的結構可靠度分析上具有相當的優勢［3-8］.當結構失效概率小于10-3時，Monte-Carlo法的計算效率較低.采用傳統響應面法對隱式功能函數的實際工程進行結構可靠度分析較理想.為了提高響應面法的計算精度及效率，許多學者針對響應面函數的形狀［9-11］、試驗取樣點的選取［2，12-15］等對響應面法進行改進.此外，呂大剛等［16-17］利用均勻設計表選取響應面函數的取樣點，提出均勻設計響應面法，并將其運用于鋼框架結構的抗震可靠度分析.金偉良等［2，18］提出基于支持向量機、最小二乘向量機的改進響應面法.Liu等［19］基于均勻設計法和雙加權回歸分析法對響應面法進行改進.趙威等［20］結合均勻設計法與偏最小二乘法來擬合響應面函數.基于人工神經網絡的可靠度分析方法能夠較好地解決隱式功能函數的結構可靠度問題［21-23］.當實際工程結構的隨機變量較多時，采用Monte-Carlo法、響應面法、人工神經網絡算法及其改進算法均具有一定的局限性.

本文結合LHS 法與均勻設計響應面法，提出基于拉丁抽樣均勻設計的混合模擬法（hybrid simulation method based on Latin hypercube sampling and uniform design response surface method，LUH）.該方法為具有多維隨機變量、隱式功能函數等特點的復雜結構可靠度問題提供了一條新的解決途徑.LUH 利用LHS法剔除不靈敏的隨機變量的影響；然后運用均勻設計法選取響應面函數的試驗點，結合JC法（國際安全聯合委員會（JCSS）推薦的一次二階矩法）計算結構失效概率，并擬合出功能函數方程.本文將LUH 法應用于2個經典可靠算例中，并將其計算精度、效率與其他經典方法進行對比分析.最后，將該方法運用于一座已建成的三跨連續剛構橋正常使用極限狀態下的可靠度分析中.

1 基本原理

1.1 拉丁超立方抽樣法

LHS法是一種多維分層抽樣方法，基本思想如下：將每一個隨機輸入變量Xi的分布函數域在概率上N 等分為（k＝1，2，…，N ），對每個子區間進行獨立等概率抽樣，在每一次確定性計算分析中嚴格保證在每一子區間抽樣一次［3-4］.為了保證抽取的隨機數屬于各子區間，第i個子區間內的隨機數Vi須滿足以下條件：

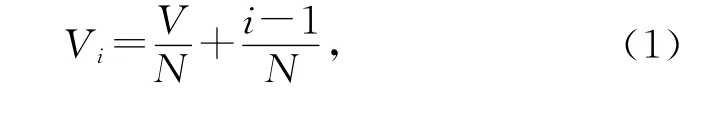
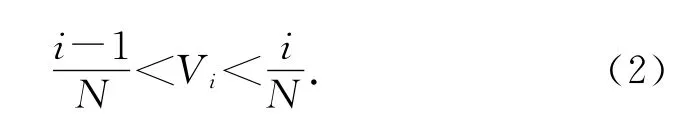
式中：i＝1，2，…，N；Vi為第i個子區間的隨機數；V為［0 ，1］ 區間均勻分布的隨機數.

對n 維隨機變量Xi（i＝1，2，…，n）進行LHS抽樣設計包括以下2個步驟［4］.

2）對每個隨機變量Xi提取一個樣本代表X并按照隨機編號排列，對所有隨機變量的樣本都按照隨機編號進行排列，從而形成N 個隨機排列.每個排列均包含全部隨機變量的一個樣本代表.例如2 個隨機變量10 次模擬的LHS 抽樣設計如圖1所示.

LHS抽樣法具有抽樣記憶功能，可以避免直接抽樣法數據點集中而導致仿真循環重復的問題.它在抽樣過程中強制抽樣點必須離散分布在整個抽樣空間.當隨機輸入變量的個數n 較大時，采用LHS法能夠極大地減少抽樣次數，且能夠達到直接抽樣法的同等精度.

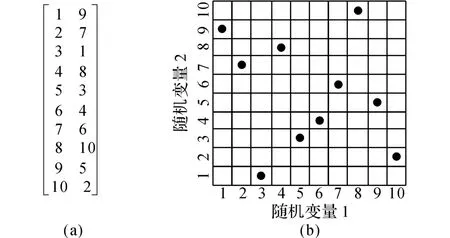
圖1 2個隨機變量10次模擬的LHS法抽樣數據Fig.1 Latin hypercube sampling table for two variables and ten runs

1.2 均勻設計響應面法

均勻設計方法是由我國數學家王元和方開泰于1978年提出的［24］.與具有均勻分散、整齊可比兩大特點的正交設計方法相比，均勻設計只考慮試驗取樣點在試驗范圍內均勻散布.

對于多因素、多水平試驗設計，均勻設計是一種對模型的變化有一定穩健性的方法.假如須對s個因素進行試驗設計，設x1，x2，…，xs的試驗區域為Cs＝［0，1］s，回歸模型為

式中：g 為某已知函數類（例如二次可微），但具體形式未知；ε為隨機誤差.

通過試驗估計響應在試驗區域Cs上的平均值，即

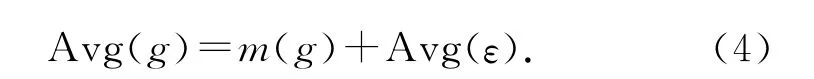
由于試驗誤差Avg（ε）在Cs上的平均值接近于0，則

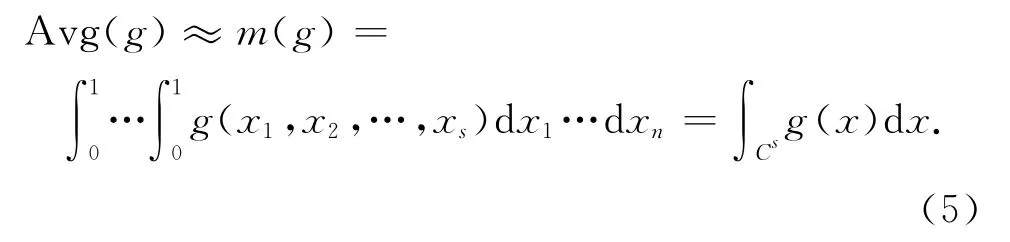
若 在Cs上 做n 次 試 驗， 試 驗 點 為 Pn＝｛xk＝ （xk1，xk2，…，xks），k＝1，2，…，n｝ ，則函數g 在n 個試驗點上的平均值為

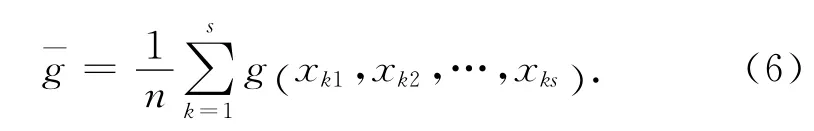
采用式（6）估計m（g） ，估計值引起的誤差可由Koksma-Hlawka不等式表示為

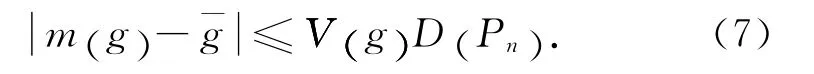
式中：V（g） 為函數g 在試驗區域Cs上的全變差；D （Pn）為試驗點集Pn在Cs上的偏差，它是度量Pn在Cs上散布均勻的測度.在試驗設計時，應當選用使D （Pn）極小的試驗點集，這是均勻設計的核心要求之一.

在數論方法中，最普遍采用L2-偏差來計算偏差D （Pn）.Warnock在1972年推導出其表達式［24］為

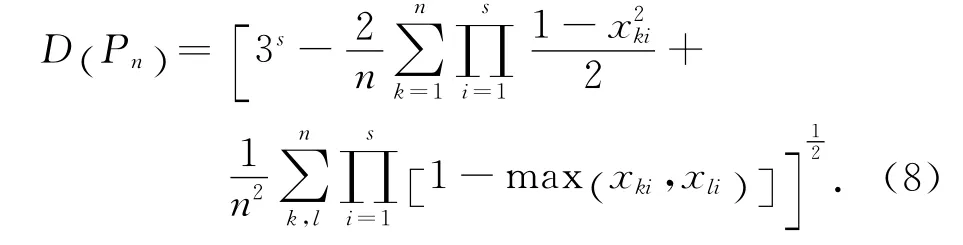
設計均勻設計表是一個優化偏差D （Pn）的過程，目前構造均勻設計表主要有好格子點法、拉丁方法、數值優化法等方法［16］.

呂大剛等［16-17］運用均勻設計法選取響應面函數的取樣點，提出均勻設計響應面法，該方法具有較好的計算精度.Liu等［19-20，22-23］對均勻設計響應面 進行改進，均取得了較好的效果.

2 基于拉丁抽樣均勻設計的混合模擬法及其實現

2.1 基于拉丁抽樣均勻設計的混合模擬法

本文將LHS 法與均勻設計響應面法相結合，提出一種基于拉丁抽樣均勻設計的混合模擬法.該方法綜合了LHS 法和均勻設計響應面法的優點，使兩者互為補充，其較Monte-Carlo法可以節省大量的計算時間.此外，混合模擬法通過對隨機輸入變量的可靠性靈敏度因子的分析，忽略靈敏度較低的隨機輸入變量的影響，減少了隨機輸入變量的數目，從而可以減少均勻設計響應面法循環的次數、提高計算效率，且計算精度較高.混合模擬法的流程如圖2所示.

基于拉丁抽樣均勻設計的混合模擬法的基本步驟如下.

1）對結構進行200～1 000次LHS抽樣，計算各隨機輸入變量的可靠性靈敏度因子.

假如結構中存在n個服從一定分布的隨機變量x1，x2，，…，xn，聯 合 概 率 密 度 分 布 函 數 為fx（x1，x2，…，xn），結 構 極 限 狀 態 函 數 為G （x1，x2，…，xn）：G （x1，x2，…，xn）＞0表示結構安全；G （x1，x2，…，xn）＜0 表 示 結 構 失 效；G （x1，x2，…，xn）＝0表示結構處于臨界狀態.

結構失效概率為

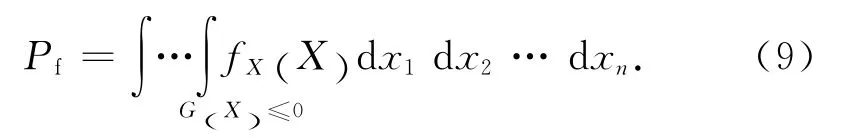
式中：X 為由變量x1，x2，…，xn表示的隨機變量矢量.

設各隨機變量的平均值、均方差的一般表達式為μxi、σxi，具體數值為，則各隨機變量xi對結構失效的靈敏度為各隨機變量的靈敏度因子為

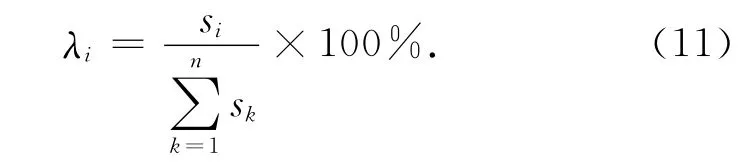
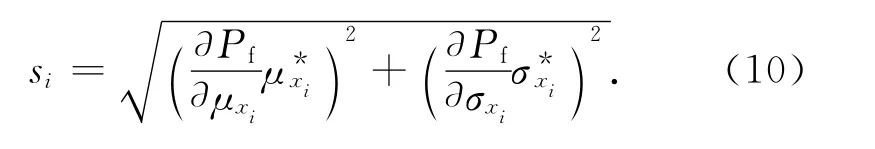
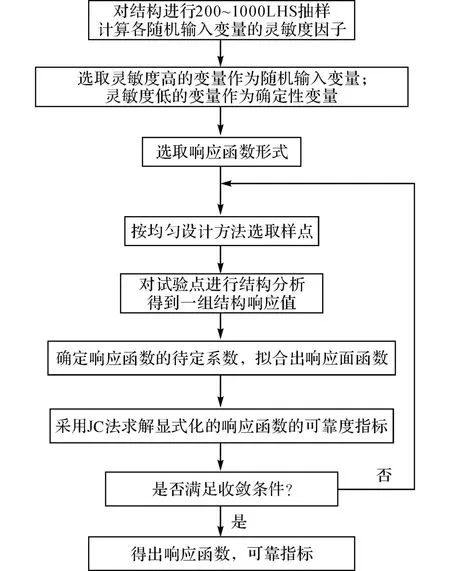
圖2 基于拉丁抽樣均勻設計的混合模擬法流程圖Fig.2 Flow chart of LUH method

由于Pf通常不能由關于μxi、σxi的函數顯式表達，張偉［25］提出采用下式近似計算靈敏度：

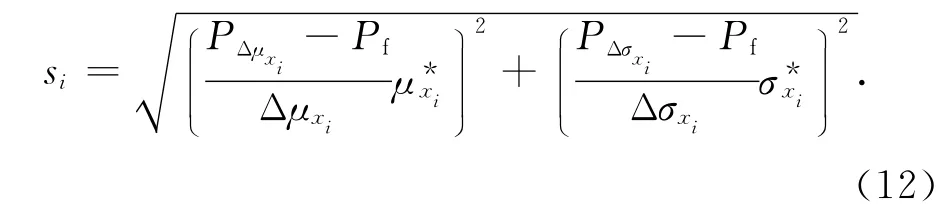
式中：PΔμxi為以μxi＋Δμxi替代μxi、而其他隨機變量不變時的結構失效概率，PΔσxi為以σxi＋Δσxi替代σxi、而其他隨機變量不變時的結構失效概率，Pf為以平均值、均方差計算出的結構失效概率.

2）將計算所得的可靠性靈敏度因子按其大小進行排序，將靈敏度較高的輸入變量繼續作為隨機變量考慮，靈敏度較低的隨機輸入變量按確定性變量考慮.通常取2.5% 為臨界值，當靈敏度因子≥2.5% 時認為靈敏度較高，當靈敏度因子＜2.5%時認為靈敏度較低［25-26］.

3）選取能夠體現真實極限狀態方程主要特點的響應面函數形式.通常選取不考慮交叉項的二次多項式為響應面函數：

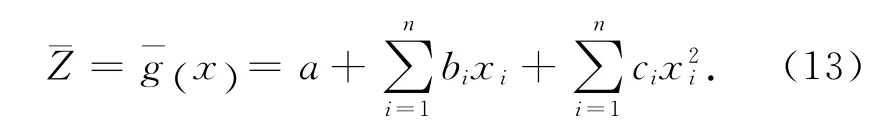
式中：a、bi、ci為回歸系數.

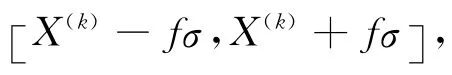
7）由于式（13）中有2n＋1個回歸系數，利用步驟6）中所得的2n＋1個結構響應，可以求解a、bi、ci（i＝1，2，…，n） ，從而確定均勻設計響應面函數，即為極限狀態方程.

8）利用JC法求解顯式化功能函數的可靠度指標β（k）以及設計驗算點，其中k為迭代次數.

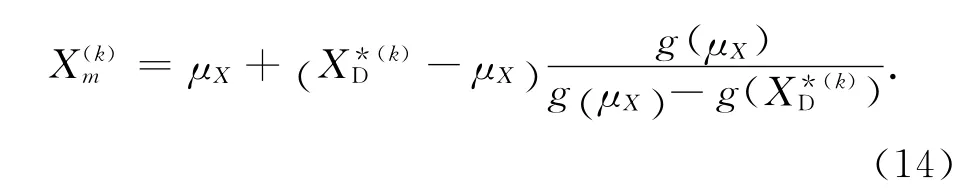
新插值點較接近真實的極限狀態曲面，以新插值點為展開點進行下一輪迭代，重復步驟5）～9），直到滿足收斂條件為止.

2.2 基于拉丁抽樣均勻設計的混合模擬法的實現

利用Matlab語言及軟件Ansys可以實現基于拉丁抽樣均勻設計的混合模擬法.首先利用Ansys可靠度分析模塊（PDS）中Monte-Carlo法的LHS抽樣對結構進行200～1 000次抽樣，據此計算各隨機輸入變量的可靠性靈敏度因子.按照靈敏度因子的大小排序，將靈敏度因子≥2.5%的輸入變量繼續作為隨機變量考慮，同時將靈敏度因子＜2.5%的隨機輸入變量作為確定性變量考慮.在Matlab中根據好格子點法理論，編制使中心化L2-偏差最小的均勻設計表程序［27］，按照生成的均勻設計表選取各隨機變量的取樣點，并形成對應的均勻設計數據文件.在Ansys可靠度分析模塊（PDS）中響應面的用戶自定義接口中讀入均勻設計數據文件，擬合出均勻設計響應面函數，即為顯示化的功能函數.在迭代過程中，借助Matlab編制JC 法程序求解顯式化功能函數的可靠度指標及設計驗算點.整個方法實現的基本原理及流程如圖3所示.當可靠度指標達到計算收斂精度時，上述計算過程退出迭代循環.

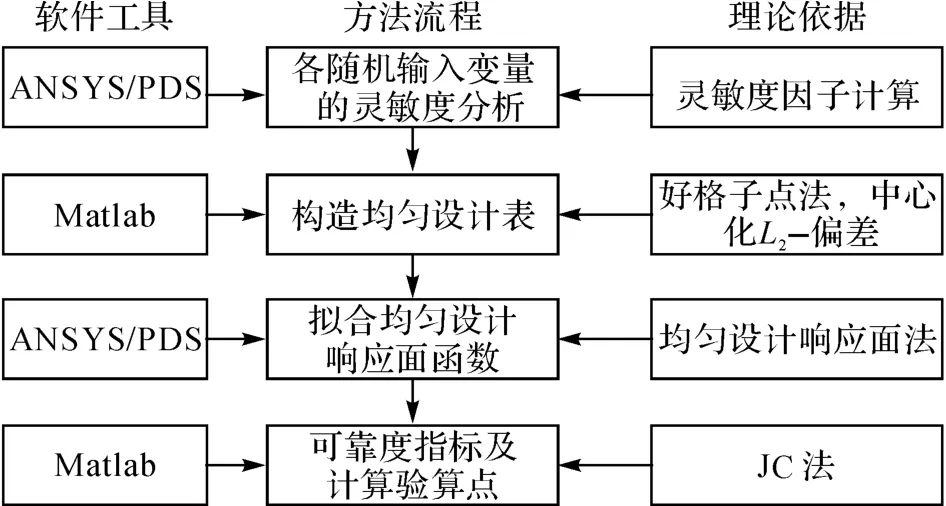
圖3 基于拉丁抽樣均勻設計的混合模擬法的基本原理及流程圖Fig.3 Principle and flow chart of LUH method

3 算例分析

為了驗證基于拉丁抽樣均勻設計的混合模擬法的適用性，將該方法應用于2個具有較多隨機變量、隱式功能函數的經典可靠度分析算例中，并將本文方法的計算結果與傳統可靠度計算方法的結果進行對比分析.算例中的結果均列于表2、3、5、6 中.表2、3、5、6中，MC表示Monte-Carlo法，計算結果作為精確解；RSM 表示經典響應面法；IRSM 表示改進響應面法；VPSM 表示利用向量投影取樣點的響應面法；FORM 表示一次二階矩方法；LCH 表示基于拉丁抽樣中心復合設計的混合模擬法；LBH 表示基于拉丁抽樣Box-Bechnken的混合模擬法；LOH表示基于拉丁抽樣正交設計的混合模擬法；LUH 表示基于拉丁抽樣均勻設計的混合模擬法，即本文方法.表2、5的相對誤差均為結構失效概率的誤差.

算例1 如圖4所示為三跨十二層建筑的平面框架結構計算簡圖.各單元的彈性模量均為E＝2.0×107kN／m2，單元截 面 慣 性 矩Ii與 截 面 面 積Ai的關系為Ii＝αi（i＝1，2，…，5） ，其中，αi為截面特性系數，各單元的截面特征如表1所示.隨機變量為各單元的截面面積Ai，統計參數如表1 所示.外荷載P 的均值為30kN，變異系數為0.25，屬于極值Ⅰ型分布.考慮結構在正常使用的極限狀態下，根據規范給出的最大允許水平位移［u］＝H／500＝0.096m（H 為樓高），可以建立極限狀態方程：z＝0.096-uk，其中uk為k 點的水平位移.計算結構可靠指標β及失效概率Pf.

表1 隨機變量統計特性Tab.1 Statistic characteristics of random variables

對結構進行200次LHS抽樣分析，得出各隨機變量的靈敏度因 子，如圖5所示.將靈敏度因子＜2.5%的隨機變量A2作為確定性變量考慮，其他靈敏度較高的5個輸入變量作為隨機變量考慮.當運用均勻設計響應面法擬合極限狀態方程時，選用偏差為0.191 87的U1＊1（115）均 勻設 計 表 在抽 樣空間中選取試驗點.各方法對算例1的可靠度分析結果如表2所示.LCH 法、LBH 法、LOH 法以及 本文方法的取樣點分布如圖6 所示.采用RSM 法、IRSM 法、LOH 法及本文方法計算所得的設計驗算點如表3所示.

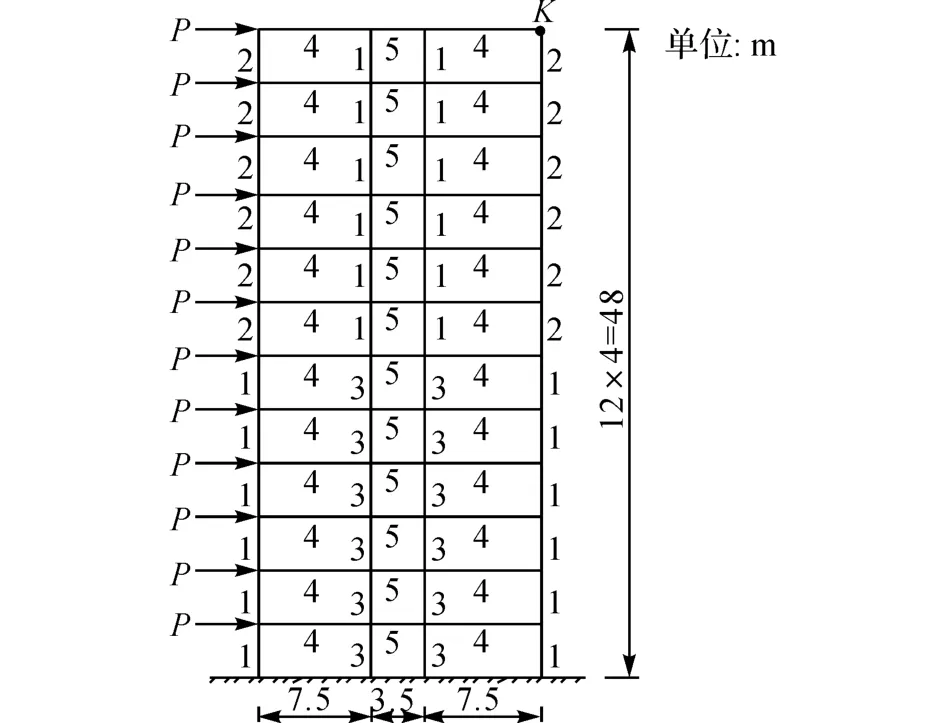
圖4 算例1的計算簡圖Fig.4 Calculation diagram of example 1

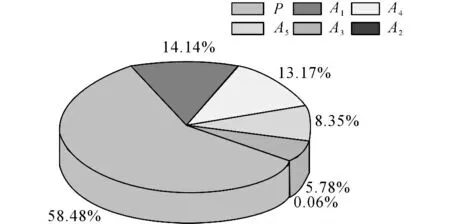
圖5 算例1的靈敏度因子Fig.5 Sensitivity factors of example 1

基于拉丁抽樣正交設計的混合模擬法擬合的功能函數表達式為

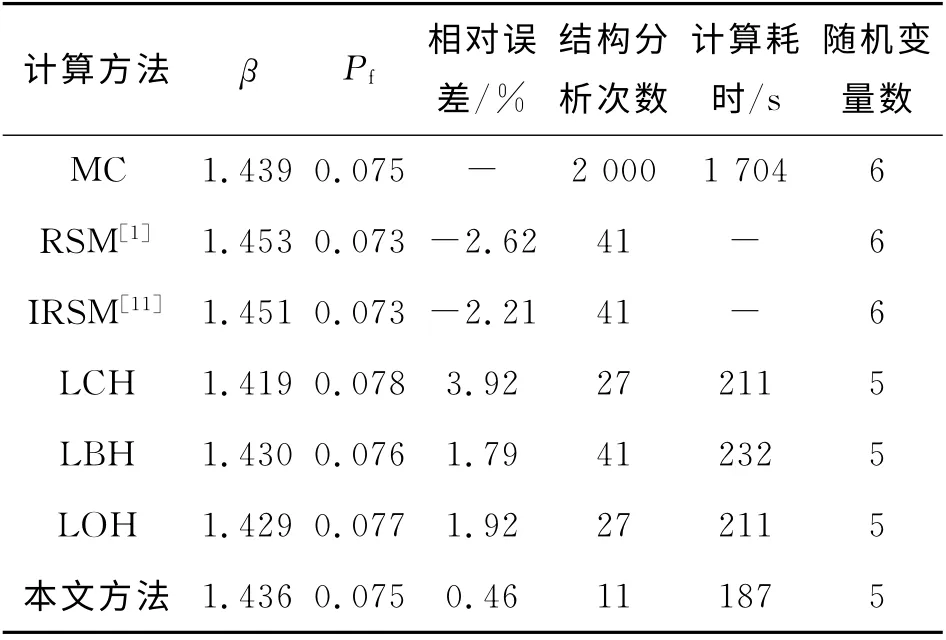
表2 算例1的可靠度分析結果Tab.2 Reliability analysis results of example 1

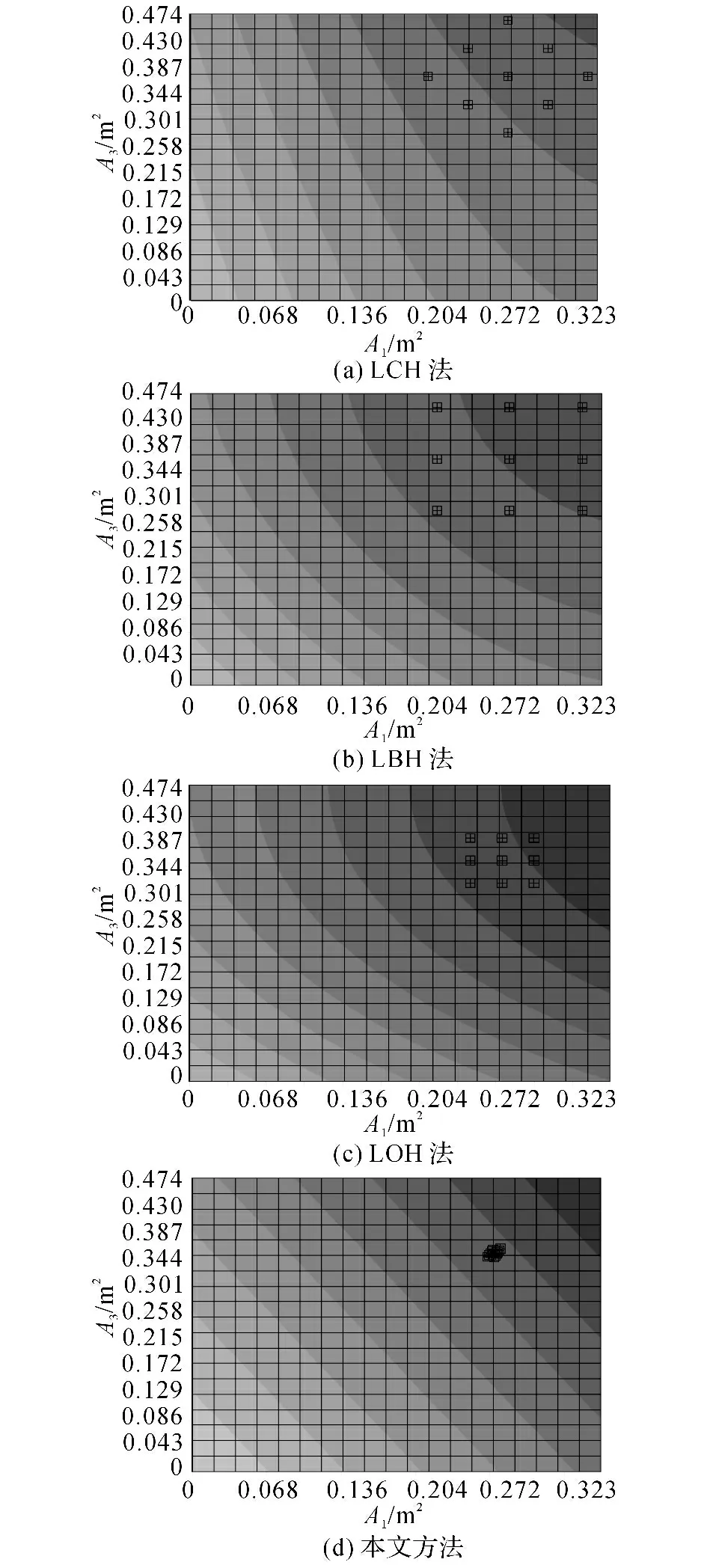
圖6 各混合模擬法取樣點分布比較Fig.6 Comparison of sample point for each hybrid simulation method

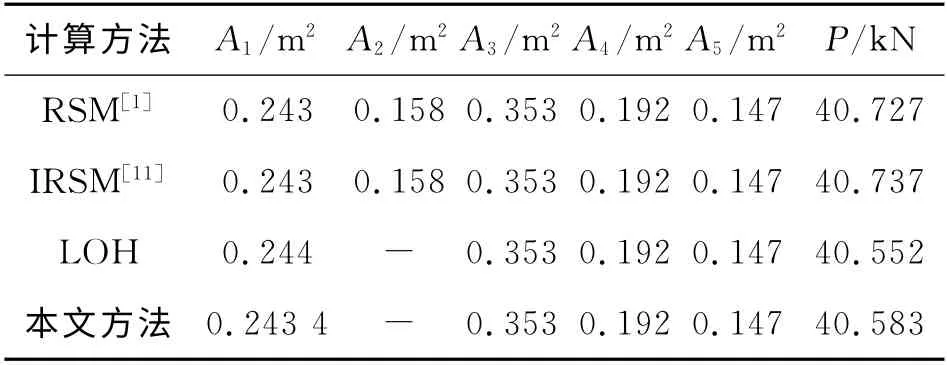
表3 算例1的設計驗算點比較Tab.3 Comparison of design points for example 1

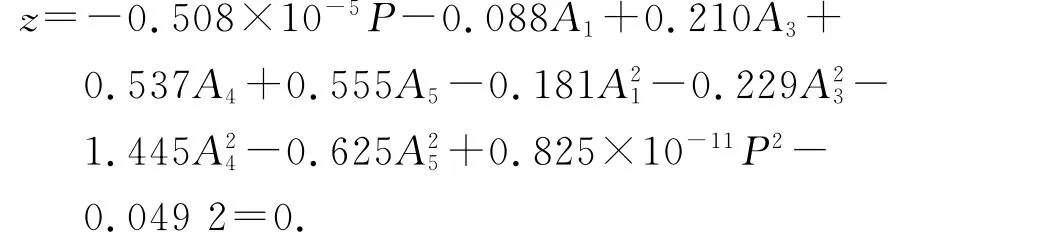
基于拉丁抽樣均勻設計的混合模擬法擬合的功能函數表達式為

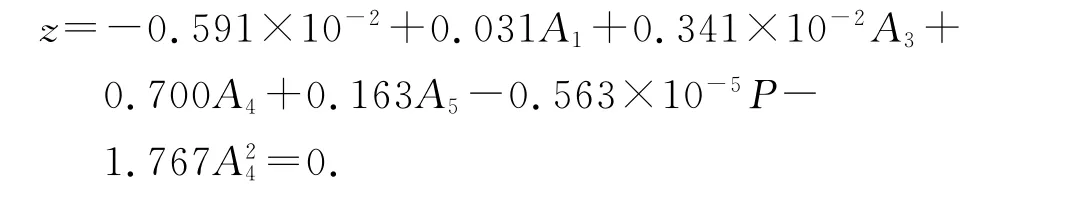
算例2 二十三桿桁架如圖7 所示，桁架結構由23個單元組成.其中，E 為彈性模量，A 為橫截面面積，輸入隨機變量的統計參數如表4所示.以桁架中點的位移 D （x） 不超過11.00cm 建立結構的極限狀態函數：g（x） ＝0.11-D （x） ，試求解結構的失效概率與可靠指標.

對結構進行200次LHS抽樣分析，得出各隨機變量的靈敏度因子如圖8 所示.將靈敏度因子＜2.5%的隨機變量E2、P1、P6作為確定性變量考慮，其他靈敏度較高的7個輸入變量作為隨機變量考慮.當運用均勻設計響應面法擬合極限狀態方程時，選用偏差為0.301 46的（157）均勻設計表在抽樣空間中選取試驗點.各方法對算例2的可靠度分析結果如表5所示.LCH 法、LBH 法、LOH 法以及本文方法的取樣點分布如圖9所示.采用LOH法、本文方法計算所得的設計驗算點如表6所示.

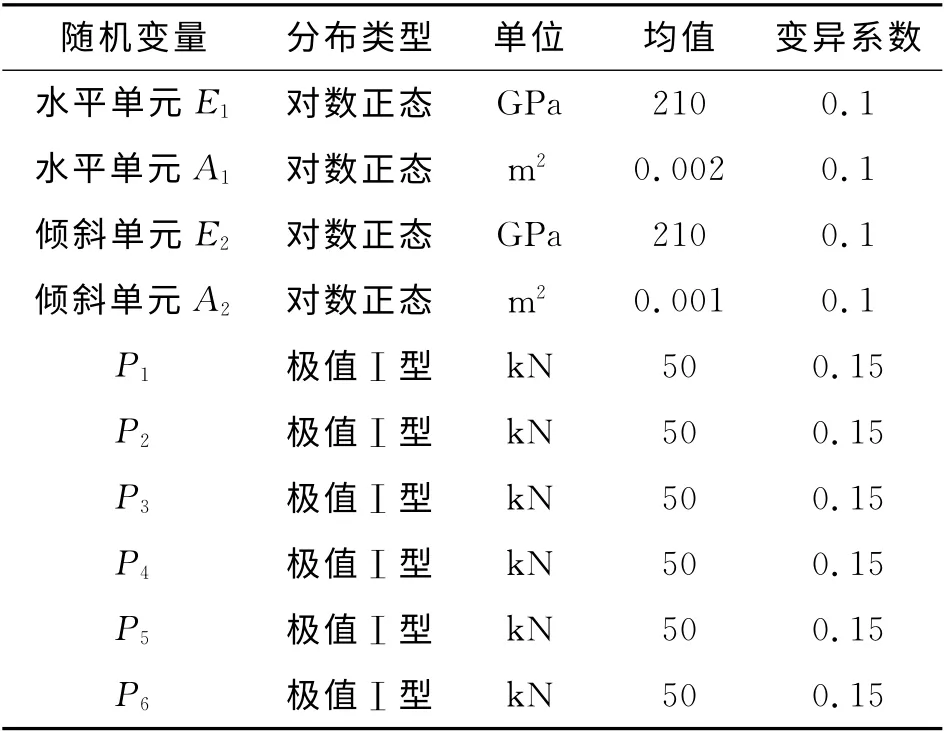
表4 隨機變量統計特性Tab.4 Statistic characteristics of random variables

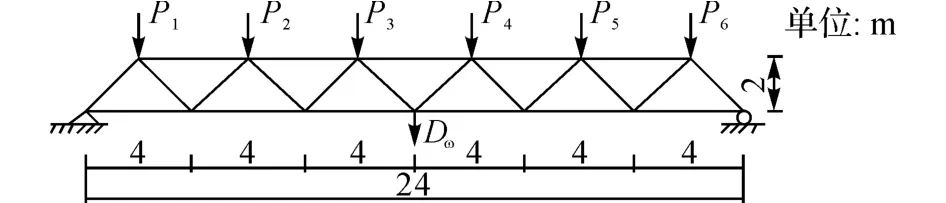
圖7 算例2的計算簡圖Fig.7 Calculation diagram of example 2

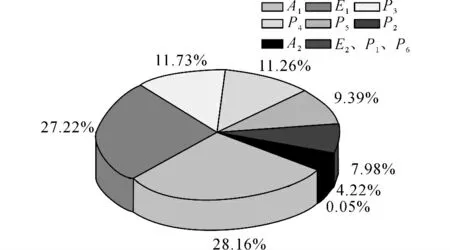
圖8 算例2的靈敏度因子Fig.8 Sensitivity factors of example 2

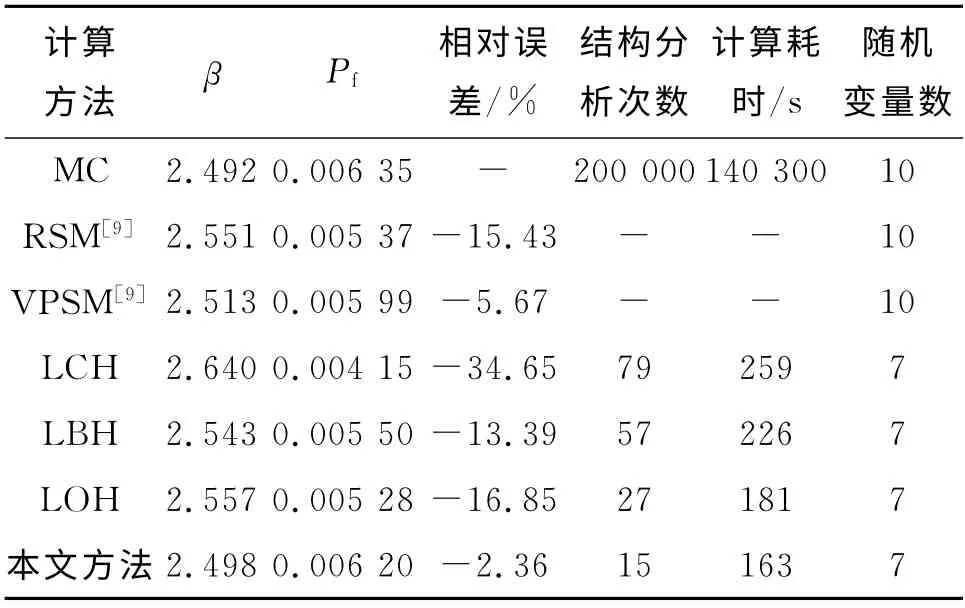
表5 算例2的可靠度分析結果Tab.5 Reliability analysis results of example 2

基于拉丁抽樣正交設計的混合模擬法擬合的功能函數表達式為

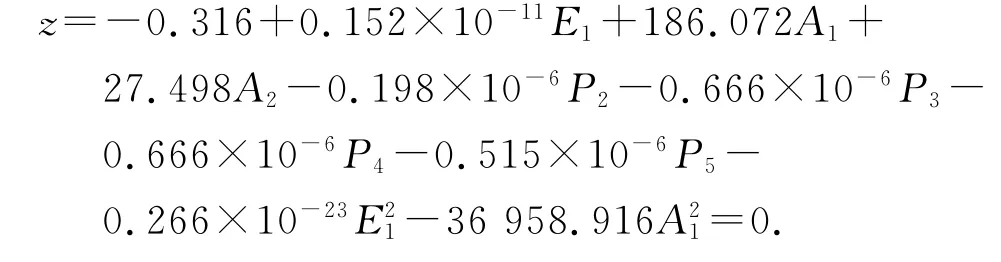
基于拉丁抽樣均勻設計的混合模擬法擬合的功能函數表達式為

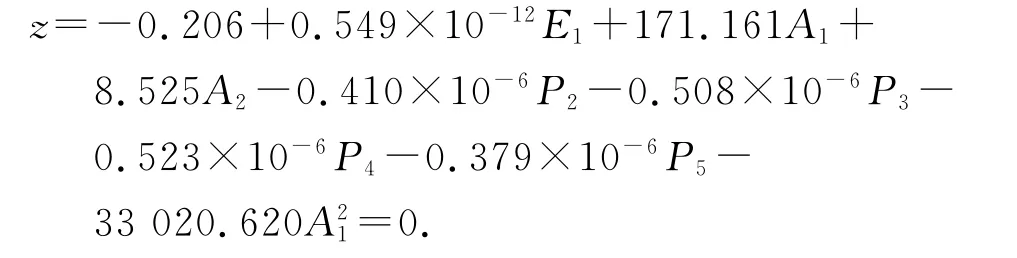
分析表2、5的可靠度計算結果可知，本文方法的計算結果最接近Monte-Carlo法的精確解，且計算耗時遠遠小于Monte-Carlo法.同時，本文方法考慮的隨機變量數少于常規響應面法，結構分析次數減少，計算效率提高.借助LHS法對隨機變量的可靠性靈敏度因子的分析，本文方法剔除了靈敏度較低的隨機輸入變量對構造響應面函數的干擾，使得計算精度較常規響應面法高.對比4種混合模擬法的計算結果可知，本文方法的精度最高、計算耗時最少.換言之，即在考慮相同的隨機變量時，均勻設計響應面法較中心復合設計響應面法、Box-Bechnken響應面法、正交設計響應面法的精度更高、計算效率更好.由此可見，本文方法是可行的，且精度較高.

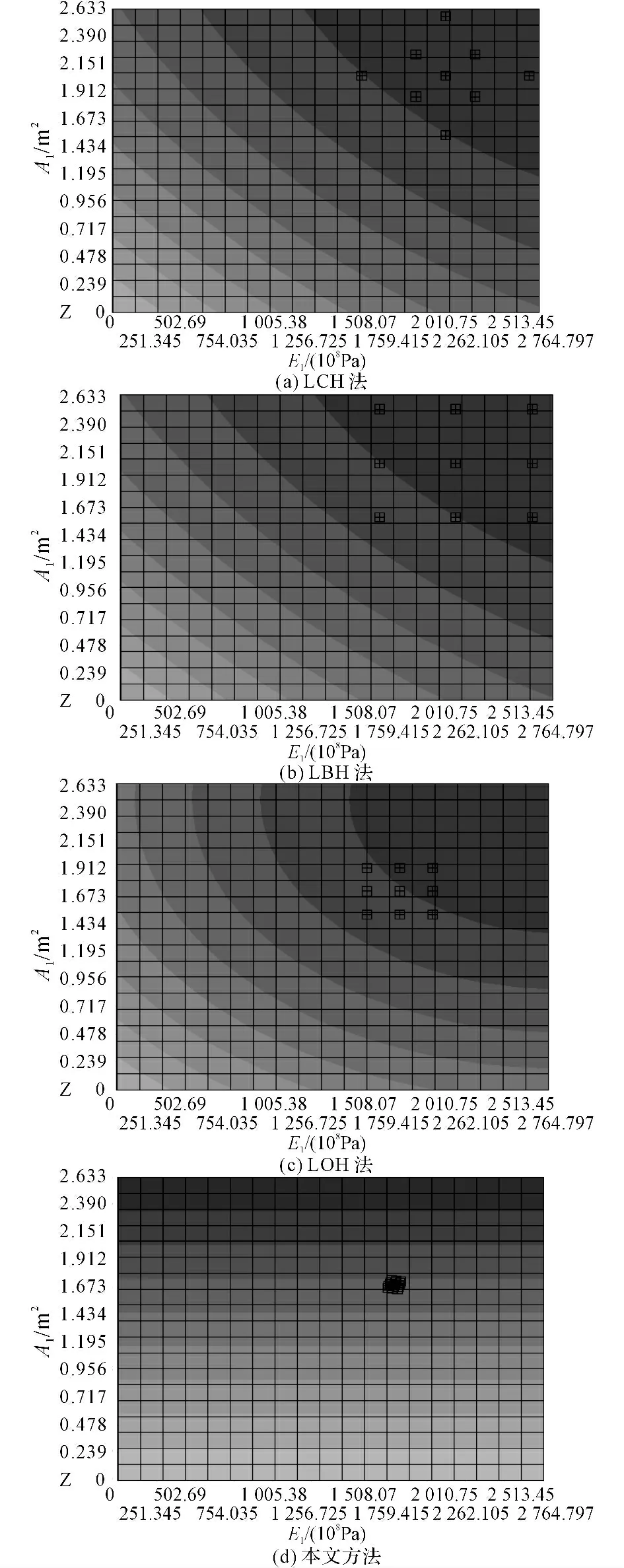
圖9 各混合模擬法取樣點分布比較Fig 9 Comparison of sample point for each hybrid simulation method

表6 算例2的設計驗算點比較Tab.6 Comparison of design points for example 2

對比圖6、9中4種混合模擬法的試驗取樣點分布情況可知，本文方法的試驗取樣點更接近設計驗算點，且在設計驗算點周邊均勻分散.表3、6的結果顯示，采用4種混合模擬法計算出的設計驗算點均較接近.

4 工程實例

某已建成的三跨連續剛構橋橫跨廣西右江主航道，上部構造采用跨徑為（85＋160＋85）m 的三向預應力混凝土連續箱梁結構，主梁采用單箱單室的箱形斷面.單箱頂寬為13.5m，底寬為7.0m，翼緣板寬為3.25m，支點處梁高9.0m，跨中及梁端梁高2.8m，梁底緣按二次拋物線變化.主墩下部構造采用雙壁式墩身，單壁寬為1.6m，兩壁中心縱向間距為8.0m.橋梁結構的總體布置圖如圖10所示.

考慮材料性能參數、幾何尺寸參數、荷載效應等的隨機性，應用本文提出的LUH 法對三跨連續剛構橋在正常使用極限狀態下中跨跨中撓度的可靠性進行分析.

根據文獻［28］中統計的材料性能參數、計算模式、幾何尺寸參數、作用效應等各種隨機變量，本文假定90項隨機變量，由于篇幅有限，僅將部分隨機變量列于表7.在正常使用極限狀態下，根據規范《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTG D62-2004）可知，連續剛構橋的主梁在車輛荷載作用下的最大豎向撓度不應超過計算跨徑的1／600，據此建立極限狀態方程：

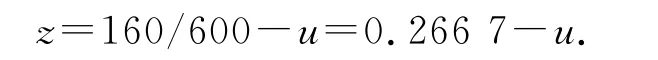
式中：u為三跨連續剛構橋中跨跨中豎向撓度.根據LUH 法可知，u可以表示為靈敏度因子較高的隨機變量的函數.

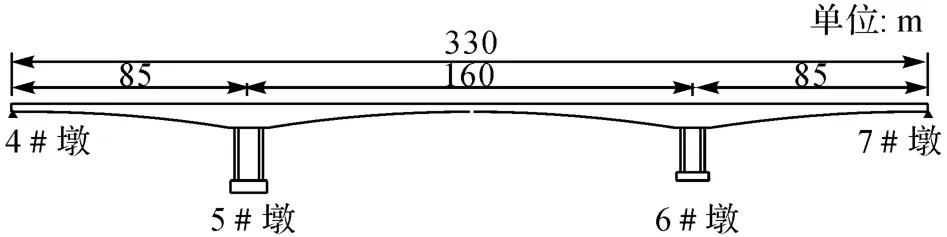
圖10 連續剛構橋總體布置圖Fig.10 Elevation view of continuous rigid frame bridge

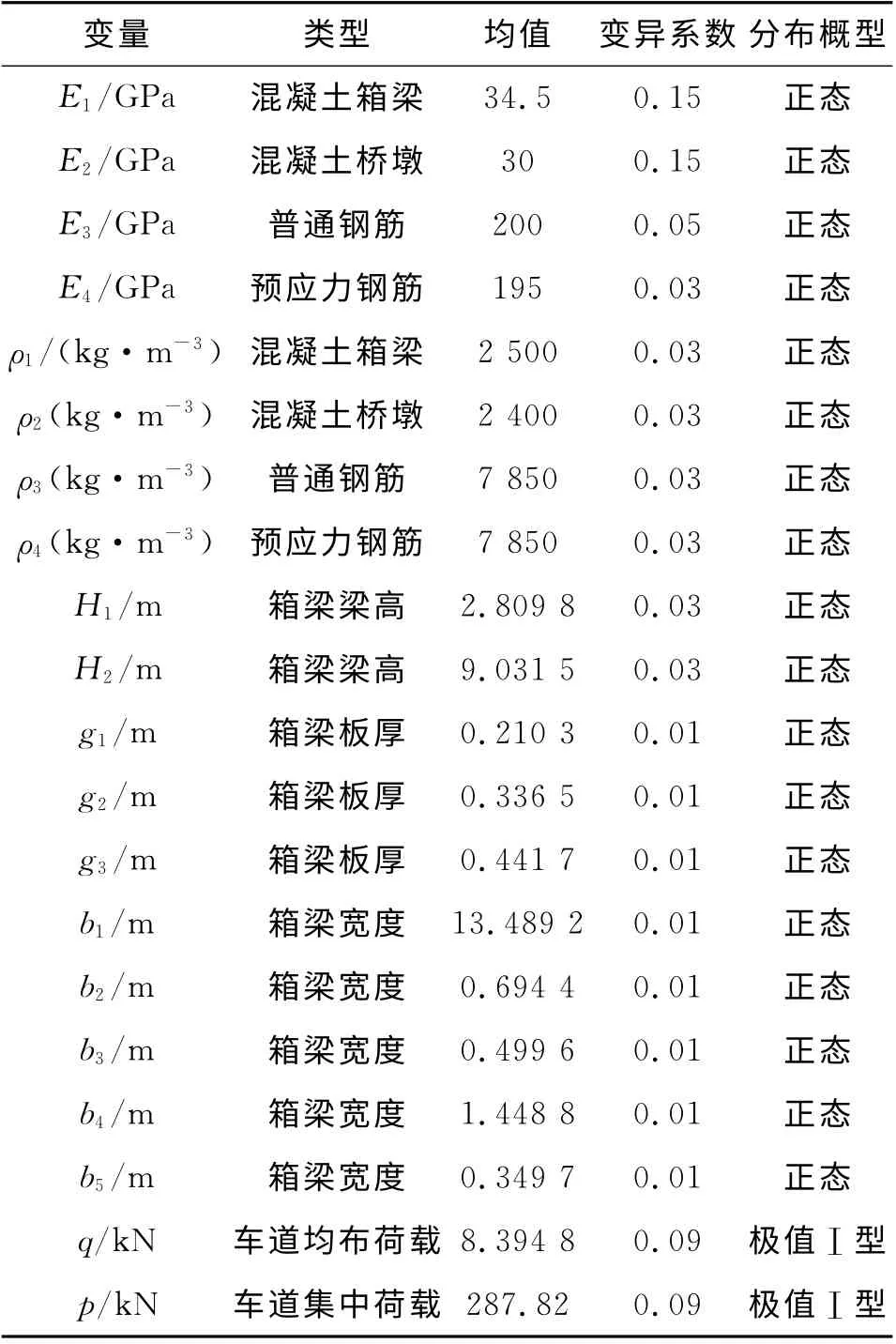
表7 隨機變量統計特性Tab.7 Statistic characteristics of random variables

利用ANSYS對連續剛構橋進行確定性結構分析.在ANSYS／Structural中建立三維有限元模型（見圖11），共計18 784個單元，29 105個結點.利用ANSYS／PDS對連續剛構橋進行500次LHS抽樣分析，得出各隨機變量的靈敏度因子如圖12所示.將靈敏度因子＜2.5%的隨機變量作為確定性變量考慮，其他靈敏度較高的8個輸入變量作為隨機變量考慮.當運用均勻設計響應面法擬合極限狀態方程 時，選用偏差為0.339 1的（178）均勻設計表在抽樣空間中選取試驗點.采用LOH 法、本文方法計算所得的可靠性指標及設計驗算點如表8所示. 基于拉丁抽樣均勻設計的混合模擬法擬合的功能函數表達式為

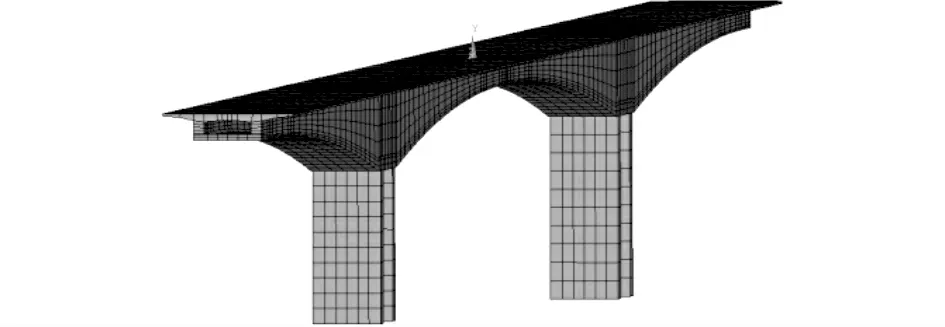
圖11 連續剛構橋有限元模型Fig.11 Finite element model of continuous rigid frame bridge

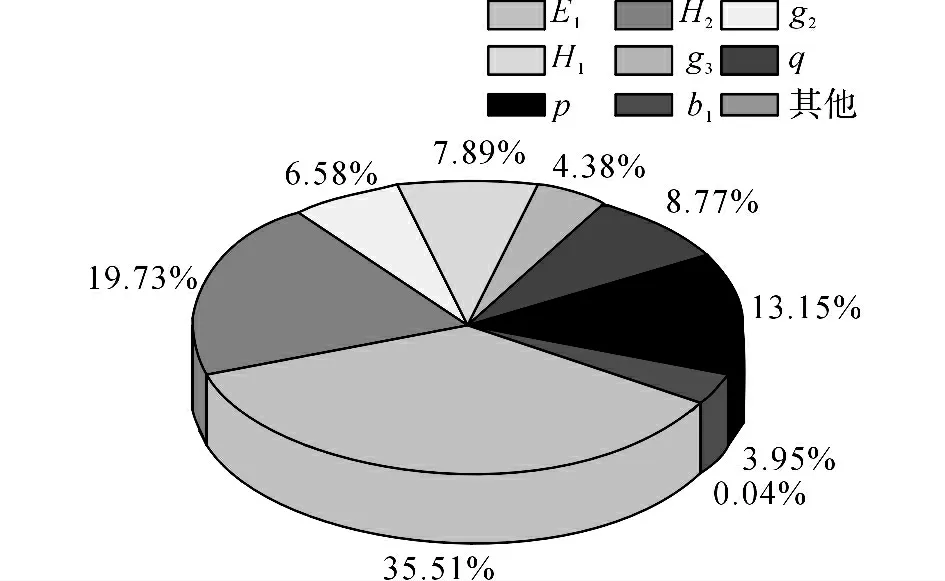
圖12 靈敏度因子圖Fig.12 Chart of sensitivity factors

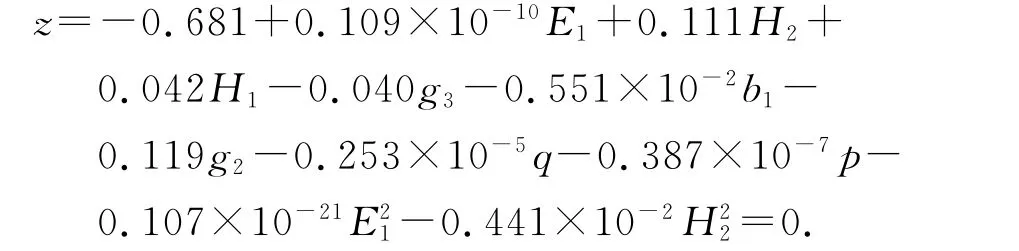
由于對該連續剛構橋進行一次確定性結構分析的時間較長，若采用Monte-Carlo法進行可靠度分析，則多次循環所需的計算耗時更冗長，計算效率極低甚至不可行.由于考慮了90項隨機變量，若采用響應面法，則所需進行的結構分析次數過多、計算耗時過長且難以擬合出響應面函數.因此，響應面法不可行.采用基于拉丁抽樣均勻設計的混合模擬法可以解決該問題，且計算效率較高，如表8所示.

表8 連續剛構橋可靠性計算結果Tab.8 Reliability analysis results of continuous rigid frame bridge

根據文獻［14］、［28］中建議正常使用極限狀態下的目標可靠度取βT＝1.5.由此可知，該三跨連續剛構橋的中跨跨中撓度滿足規范規定的目標可靠指標要求.

5 結 論

（1）本文方法結合了Monte-Carlo法和均勻設計響應面法2種方法的優點，相對Monte-Carlo法節約了大量的計算時間，相對響應面法減少了隨機輸入變量的數量，從而減少了結構計算次數，提高了計算效率.隨著結構隨機變量的增多，該方法的計算效率優勢將進一步得到體現.本文方法為復雜結構的可靠度分析提供了一條新途徑.

（2）本文方法較基于拉丁抽樣中心復合設計混合模擬法、基于拉丁抽樣Box-Bechnken混合模擬法和基于拉丁抽樣正交設計混合模擬法具有更高的計算精度、計算效率.換言之，在考慮相同隨機輸入變量的條件下，均勻設計響應面法較正交設計響應面法、中心復合設計響應面法、Box-Bechnken設計響應面法具有更高的計算精度和計算效率.

（3）運用LHS法對結構進行抽樣分析，可以尋找出對結構可靠性影響較大的因素.在實際工程中，應對這些因素的施工質量進行嚴格控制，從而使工程結構具有較高的可靠性指標.

（

）：

［1］佟曉利，趙國藩.一種與結構可靠度分析幾何法相結合的響 應 面 方 法［J］.土 木 工 程 學 報，1997，30（4）：51-57.TONG Xiao-li，ZHAO Guo-fan.The response surface method in conjunction with geometric method in structural reliability analysis ［J］.China Civil Engineering Journal，1997，30（4）：51-57.

［2］金偉良，袁雪霞.基于LS-SVM 的結構可靠度響應面分析方法［J］.浙江大學學報：工學版，2007，41（1）：44-47.JIN Wei-liang，YUAN Xue-xia.Response surface method based on LS-SVM for structural reliability analysis［J］.Journal of Zhejiang University：Engineering Science，2007，41（1）：44-47.

［3］OLSSON A M J，SANDBERG G E.Latin hypercube sampling for stochastic finite element analysis［J］.Journal of Engineering Mechanics，2002，128（1）：121-125.

［4］熊學玉，顧煒.基于改進LHS方法的預應力混凝土結構長期 性 能 概 率 分 析［J］.工 程 力 學，2010，27（4）：163-168.XIONG Xue-yu，GU Wei.Long-term performance probabilistic analysis of PCstructure based on improved LHS method［J］.Engineering Mechanics，2010，27（4）：163-168.

［5］JIN Wei-liang.Reliability-based design for Jacket platform under extreme loads［J］.China Ocean Engineering，1996，10（2）：145-160.

［6］金偉良.結構可靠度數值模擬的新方法［J］.建筑結構學報，1996，17（3）：63-72.JIN Wei-liang.A new approach to numerical simulation of structural reliability analysis［J］.Journal of Building Structures，1996，17（3）：63-72.

［7］JIN Wei-liang.Importance sampling method in V-space［J］.China Ocean Engineering，1997，11（2）：127-150.

［8］唐純喜，金偉良，陳進.結構失效面上的復合蒙特卡羅方法［J］.浙江大學學報：工學版，2007，41（6）：1012-1016.TANG Chun-xi，JIN Wei-liang，CHEN Jin.Composite Monte Carlo method on structural failure hyperplane［J］.Journal of Zhejiang University：Engineering Science，2007，41（6）：1012-1016.

［9］CHEN Jian-yun，QIANG Xu，FAN Shu-li，et al.Improved response surface method for anti-slide reliability analysis of gravity dam based on weighted regression［J］.Journal of Zhejiang University：Science A，2010，11（6）：432-439.

［10］SOARES R C，MOHAMEDB A，VENTURINI W S.Reliability analysis of non-linear reinforced concrete frames using the response surface method［J］.Reliability Engineering and System Safety，2002，75（1）：1-6.

［11］WONG S M，HOBBS R E，ONOF C.An adaptive response surface method for reliability analysis of structures with multiple loading sequences［J］.Reliability Engineering and System Safety，2002，75（1）：1-6.

［12］KIM S H，NA S W.Response surface method using vector projected sampling points［J］.Structural Safety，1997，19（1）：3-19.

［13］王宇，王春磊，汪燦，等.邊坡可靠性評價的向量投影響應面研究及應用［J］.巖土工程學報，2011，33（9）：1434-1440.WANG Yu，WANG Chun-lei，WANG Can，et al.Reliability evaluation of slopes based on vector projection response surface and its application［J］.Chinese Journal of Geotechnical Engineering，2011，33（9）：1434-1440.

［14］張哲，李生勇，石磊，等.結構可靠度分析中的改進響應面法及其應用［J］.工程力學，2007，24（8）：111-115.ZHANG Zhe，LI Sheng-yong，SHI Lei，et al.An improved response surface method for structural reliability analysis and its application ［J］. Engineering Mechanics，2007，24（8）：111-115.

［15］李洪雙，呂震宙，趙潔.基于加權線性響應面法的支持向量機可靠性分析方法［J］.工程力學，2007，24（5）：67-71.LI Hong-shuang，LV Zhen-zhou，ZHAO Jie.A support vector method for reliability analysis based on weighted linear response surface ［J］.Engineering Mechanics，2007，24（5）：67-71.

［16］呂大剛，賈明明，李剛.結構可靠度分析中的均勻設計響應面法［J］.工程力學，2011，28（7）：109-115.LV Da-gang，JIA Ming-ming，LI gang.Uniform design response surface method for structural reliability analysis［J］.Engineering Mechanics，2011，28（7）：109-115.

［17］呂大剛，賈明明，李剛.基于均勻設計響應面法的鋼框架結構抗震可靠度分析［J］.哈爾濱工業大學學報，2011，43（4）：1-5.LV Da-gang，JIA Ming-ming，LI gang.Seismic reliability analysis of steel frame structures based on uniform design response surface method［J］.Journal of Harbin Institute of Technology，2011，43（4）：1-5.

［18］金偉良，唐純喜，陳進.基于SVM 的結構可靠度分析響應面方法［J］.計算力學學報，2007，24（6）：713-718.JIN Wei-liang，TANG Chun-xi，CHEN Jin.SVM based on response surface method for structural reliability analysis［J］.Chinese Journal of Computational Mechanics，2007，24（6）：713-718.

［19］LIU Ji，LI Yun.An improved adaptive response surface method for structural reliability analysis［J］.Journal of Central South University，2012，19（4）：1148-1154.

［20］趙威，王偉.偏最小二乘回歸在響應面法可靠度分析中的應用［J］.工程力學，2013，30（2）：272-277.ZHAO Wei，WANG Wei.Application of partial least squares regression in response surface for analysis of structural reliability［J］.Engineering Mechanics，2013，30（2）：272-277.

［21］DENG Jian，GU De-sheng，LI Xi-bing，et al.Structural reliability analysis for implicit performance functions using artificial neural network ［J］.Structural Safety，2005，27（1）：25-48.

［22］CHENG Jin，LI Q S，XIAO Ru-cheng.A new artificial neural network-based response surface method for structural reliability analysis［J］.Probabilistic Engineering Mechanics，2008，23（1）：51-63.

［23］CHENG Jin，LI Q S.Artificial neural network-based response surface methods for reliability analysis of prestressed concrete bridges［J］.Structure and Infrastructure Engineering，2012，8（2）：171-184.

［24］方開泰，馬長興.正交與均勻試驗設計［M］.北京：科學出版社，2001.

［25］張偉.結構可靠性理論與應用［M］.北京：科學出版社，2009.

［26］郭彤，李愛群，繆長青，等.數值模擬聯合算法及其在潤揚大橋可靠度評估中的應用［J］.土木工程學報，2006，39（9）：80-85.GUO Tong，LI Ai-qun，MIAO Chang-qing，et al.Combined numerical simulation method and its application on the reliability assessment of Runyang bridge［J］.China Civil Engineering Journal，2006，39（9）：80-85.

［27］曹慧榮，李莉.均勻設計表的MATLAB實現［J］.統計與決策，2008，21（6）：144-146.CAO Hui-rong，LI Li.Uniform design table in Matlab［J］.Statistics and Decision，2008，21（6）：144-146.

［28］李揚海，鮑衛剛，郭修武，等.公路橋梁結構可靠度與概率極限狀態設計［M］.北京：人民交通出版社，1997.