分數階微分局部強反射的去噪方法應用
唐瑞尹沈鴻海 何鴻鯤
(華北理工大學電氣工程學院 唐山 063000)
分數階微分局部強反射的去噪方法應用
唐瑞尹*沈鴻海 何鴻鯤
(華北理工大學電氣工程學院 唐山 063000)
針對具有強反射的表面光條圖像出現散斑或復合散斑等嚴重噪聲情況,該文提出一種利用分數階微分增強的圖像去噪聲的處理算法,突出噪聲的顆粒化特征,通過連通區域面積統計的方法對有效連續光條進行分離并去除散斑噪聲,獲得有效光條圖像,最后利用灰度重心法提取有效光條的中心。經實驗對比,該方法得到的信息熵值和光條中心提取精度都顯著提高,體現了分數階微分算法增強圖像高頻信息的同時,有效保留更多的低頻信息的特點,保留了更多的圖像紋理細節,顯著提高了特征光條中心提取精度。
圖像去噪;分數階微分;強反射;光條中心提取;熵
1 引言
在結構光視覺測量系統中,關鍵任務之一是提取圖像特征光條的中心坐標[1]。激光光條中心坐標的提取精確度直接影響到了最終被測點的3維世界坐標測量精度[2]。
常見的光條中心線提取方法有灰度重心法、極值法、梯度閾值法和利用Hess矩陣的Steger方法[3,4]等。這些光條中心提取算法主要是根據光條具有高斯分布中心對稱的特點進行計算的。但是當激光投射到強反射區域,大量存在模糊散斑,造成CCD攝像機接收到的光條的橫截面光強不呈高斯分布。那么這些基于高斯分布的光條中心提取方法就不適用了。
本文在對現有特征光條提取方法分析的基礎上,結合強反射表面散斑的特點提出了基于分數階微分的特征光條中心高精度提取方法,在實驗中對其測量精度和誤差進行評估。
2 強反射表面光條中心提取
2.1 強反射表面的光學特性分析
根據物體表面的反射特性,可將物體表面劃分為朗伯(Lambert)表面、鏡面以及反射特性介于兩者之間的混合反射特性表面(以下簡稱混合表面)[5,6]。針對Lambert表面,采用基于光刀法的3維形貌測量精度較高,效果較好。而對于鏡面反面,一般具有較強的鏡面反射[7]。當激光投射到該表面后,會形成模糊的散斑。如圖1(a)所示,圖1(b)為其局部放大圖,圖1(c)為圖1(b)中白色直線對應的灰度分布圖。為有效提取強反射表面光條中心的位置,Kokku和Brooksby提出了模板法[8],該方法利用一種特殊的圖像模板來將有效信息和噪聲區分開,從而達到有效提取光條中心的目的。但是這種模板僅符合部分已進行過深入研究的測量表面,而不能用以進行較復雜或任意測量形態的研究[9]。
2.2 強反射表面光條中心提取
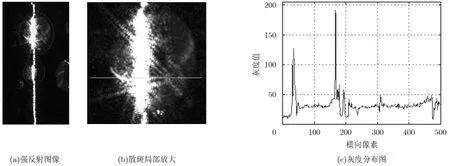
圖1 強反射表面的光條散斑圖像及其灰度分布圖
強反射表面的散斑噪聲與有效連續光條在于條紋的灰度離散程度差異,即顆粒狀與連續條紋的區別。因此,本文首先利用分數階微分增強圖像的處理方法,突出噪聲的顆粒化特征。接下來再通過連通區域面積統計的方法對有效連續光條和散斑噪聲進行分離并去除散斑噪聲,得到準確度更高的光條圖像。最后通過常規的灰度重心法獲取光條中心即可。算法的流程設計如圖2所示。
在該算法中,關鍵是在增強顆粒感明顯的散斑噪聲同時要保持灰度連續的有效條紋的圖像區域。而目前的圖像增強算法,如空域法、頻域法等都無法徹底解決強化高頻信息就會降低低頻信息這種問題。如直方圖均衡化方法增強了圖像中的高頻部分并使輸出圖像直方圖近似服從均勻分布,而對于邊緣部分過度銳化,會對紋理細節的識別產生影響[10];線性濾波方法則過度平滑了圖像低頻信息,但對增強圖像的邊緣等高頻部分作用很小;整數階微分梯度算子(一階微分算子如 Sobel, Prewitt, Canny算子;二階微分如Laplace二階微分算子)通常在突出圖像中的細節或是增強模糊的細節效果明顯, 但是造成低頻分量信息損失嚴重。而分數階微分在增強了高頻分量的同時也保留了低頻分量的信息,從而能有效克服整數階微分算子圖像增強中的缺點,在圖像處理領域也表現出了強有力的生命力。
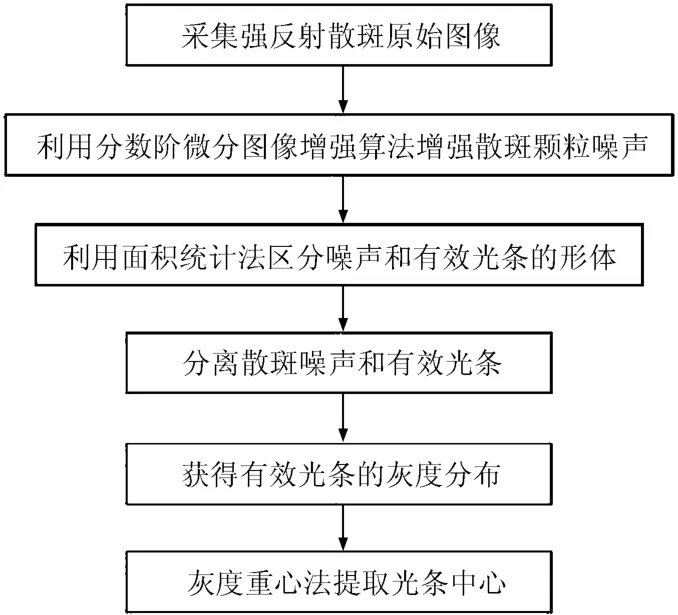
圖2 強反射區域光條中心提取算法
3 分數階微分圖像增強
3.1 分數階微分
目前常用的GrUmwald-Letnikov分數階微積分是在Euclid測度下定義的,是將微積階次從整數推廣到分數的結果,也就是說,分數階微積分的 G-L定義是將微積分階次從整數階變換到了分數階。依據規定,在Euclid測度空間發生的物理狀態與過程完全可以應用在Euclid測度下定義的分數階微積分描述和論證,對于這個分數階微分的定義如下[11]:
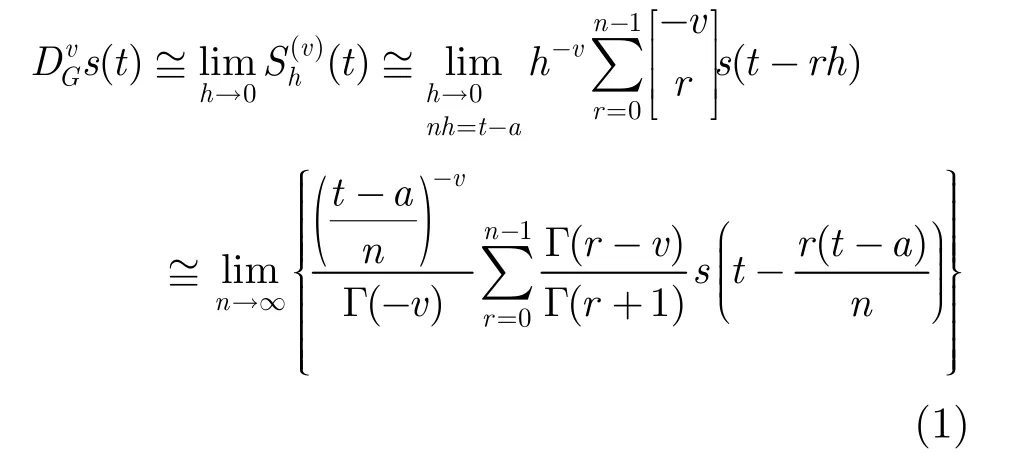
式中,Gamma函數
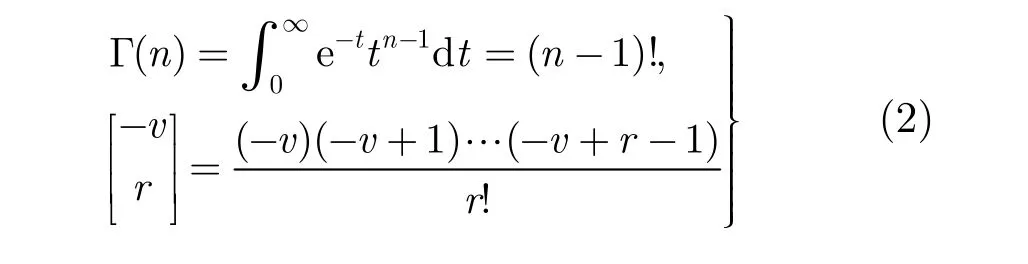
3.2 分數階微分圖像增強算法
根據式(1),2維數字圖像函數 f(x,y)對自變量x和y分別求分數階偏微分得到數值多項式和,其對應的后向差分近似表達式分別為式(3)和式(4)所示。
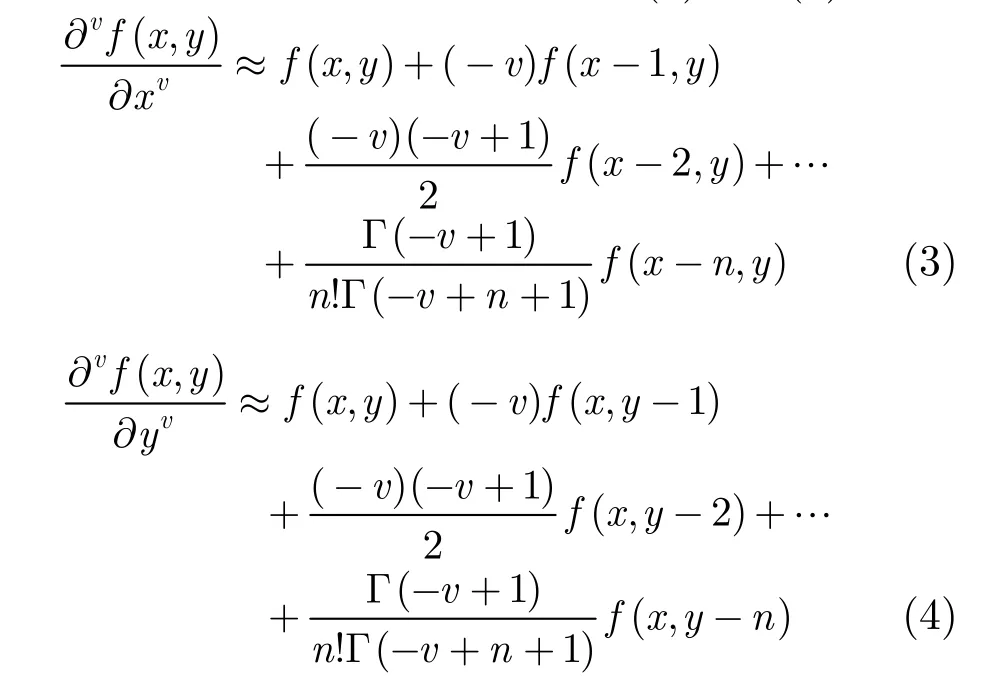
4 分數階微分圖像增強性能評價
4.1 比例尺的設定實驗
為了驗證分數階微分對圖像增強的卓越性,分別選擇2類樣本圖像:街道(street)圖像和硬盤光條強反射圖像。圖3,圖4分別展示了將2類樣本用Laplace增強、Sobel增強和本文的分數階微分增強的方法效果對比。
信息論中熵可以作為刻畫圖像紋理特征的有效參數[12]。圖像2維熵的定義為
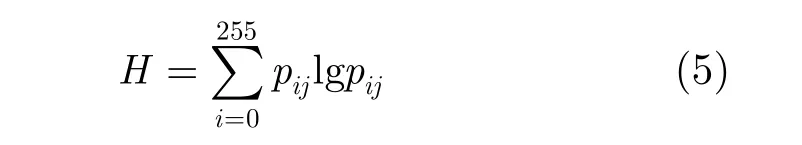
式中, pij=f(i,j)/N2, i表示像素灰度值(0 ≤i≤ 255), j表示鄰域灰度(0 ≤ j≤ 255), f(i,j)為特征二元組(i,j)出現的頻率,N為圖像的尺度。熵值越大,表面圖像信息量越大,紋理越豐富。表1中記錄了增強后各圖的熵值。
從表1可見,分數階微分增強后的leaf, street及硬盤圖像要比整數階微分增強后的這些圖像的熵值大。即分數階微分算法保留了更多的圖像紋理信息,達到了增強圖像高頻信息的同時,保留了更多的低頻信息[13]的效果。
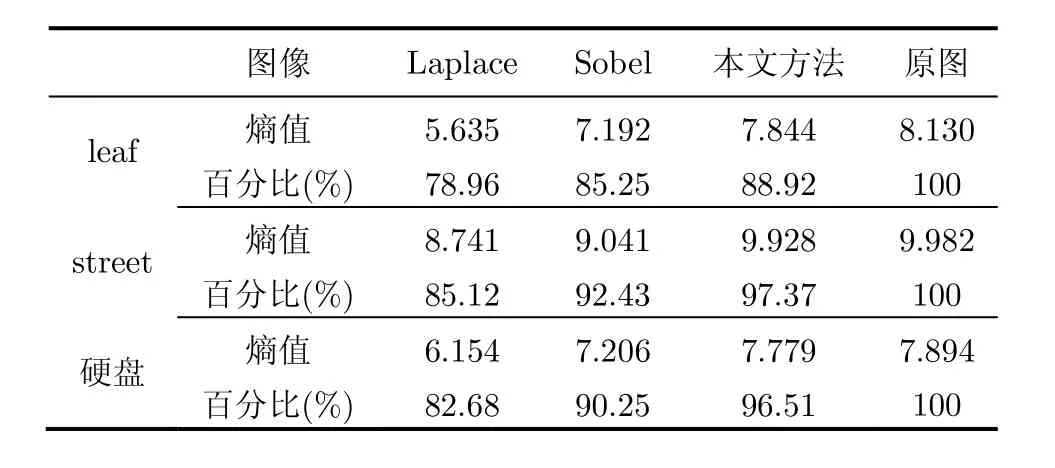
表1 3種算法增強后的熵值
利用分數階微分將強反射的散斑噪聲增強后,并與保留下來的連續有效條紋有效分離開后,就可以利用常規的灰度重心法進行提取了。

圖3 street樣本增強效果對比
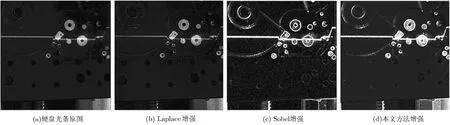
圖4 硬盤樣本增強效果對比
4.2 光條中心提取精度
如圖5所示為硬盤局部反射區域的光條圖像,用 Laplace法去噪后再用灰度重心法求取其光條中心如圖 5(a)所示,右圖黑色橢圓標出強反射區域光條中心提取失敗;用本文算法后提取的光條中心結果如圖5(b)所示。在暗背景暗光條下拍攝圖像進行光條中心提取結果如圖 5(c)所示,強反射區域的光條中心提取成功。同樣,以圖5(c)提取結果為基準,圖5(a),圖5(b)提取結果與圖5(c)誤差對比如圖5(d)所示。本文算法對硬盤的光條中心提取誤差優于其它傳統方法。
4.3 結構光視覺測量中的應用
采用線結構光視覺檢測系統對被測對象計算機硬盤進行掃描測量。由于硬盤表面多處具有強反射區域。圖6所示為直接用灰度重心法提取各個掃描光條中心后掃描測量得到的2維物體輪廓圖,從圖中白色方框部分可以明顯看出,光條中心提取失敗,造成圓形輪廓缺失,誤差很大,硬盤其它強反射的很多區域也出現了這種現象。
應用分數階微分方法對強反射區域進行增強后,然后利用上述方法進行光條中心提取,相應的2維輪廓圖如圖7所示。顯然,白色矩形框中強反射區域的輪廓更加清晰準確。
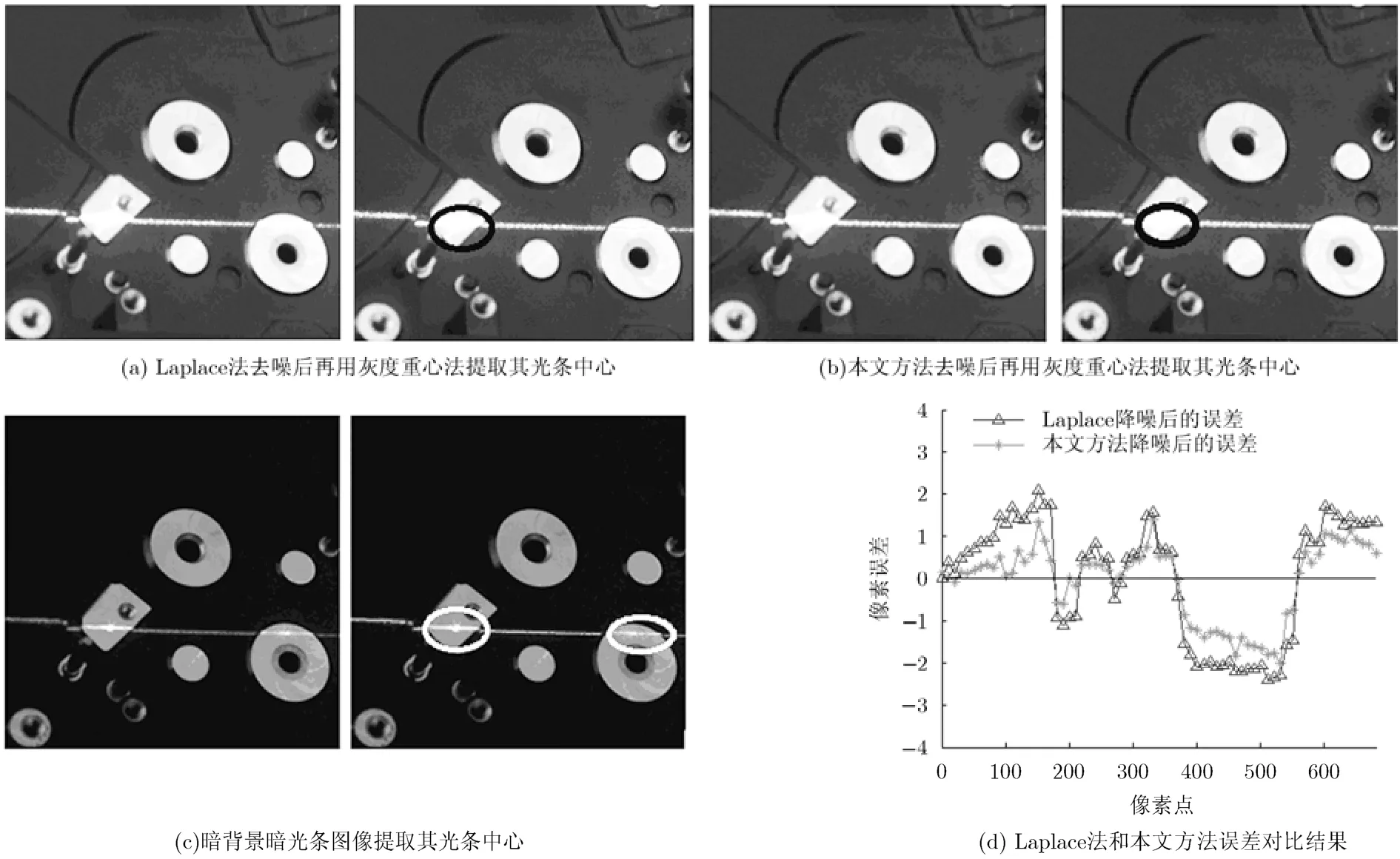
圖5 Laplace法和本文方法光條中心提取及誤差對比結果

圖6 直接用灰度重心法提取后的2維輪廓圖
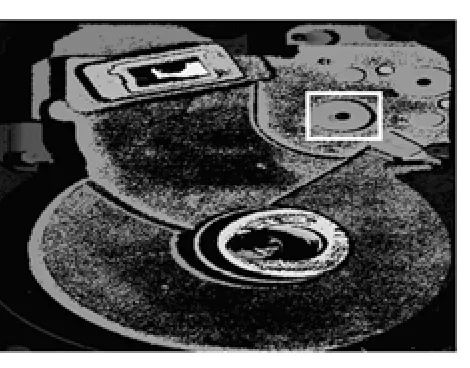
圖7 應用分數階微分 算法后的2維輪廓圖
5 結論
本文通過分析強反射表面反射特性,提出了一種基于分數階微分先增強散斑的顆粒狀,再利用面積統計的方法分離散斑,提取有效條紋光條中心的算法,給出了具體的算法流程。選用了包括硬盤在內的2類樣本分別用Laplace, Sobel和本文的分數階微分算法做圖像增強實驗,并利用信息熵做出定量對比,結果利用分數階微分算法對圖像增強后信息熵值明顯提高,均在88%以上,光條中心提取的精度明顯提高。同時將該算法應用在線結構光視覺測量計算機硬盤形貌中,在硬盤表面多處強反射區域2維輪廓清晰,有效克服原來強反射區域數據缺失的現象。分數階微分增強算法不僅增強了圖像的高頻信息,同時有效保留更多的低頻信息的特點,保留了更多的圖像紋理細節,有效克服整數階微分算子圖像增強中的缺點,為強反射物體表面的結構光視覺測量的精度提供有力的保障。
[1] 宋佳, 孫長庫, 王鵬. 錫膏激光掃描三維測量系統光強自適應調節技術[J]. 傳感技術學報, 2012, 25(8): 1166-1171. Song Jia, Sun Chang-ku, and Wang Peng. Techniques of light Intensity adaptive adjusting for the 3D measurement system of the solder paste[J]. Chinese Journal of Sensors and Actuators, 2012, 25(8): 1166-1171.
[2] 陳慶利, 黃果, 秦洪英. 數字圖像的分數階微分自適應增強[J].計算機應用研究, 2015, 32(5): 1597-1600. Chen Qing-li, Huang Guo, and Qin Hong-ying. Adaptive fractional differential algorithm for image enhance ment[J]. Application Research of Computers, 2015, 32(5): 1597-1600.
[3] Zuo Li-juan, Bai Cui-xia, Yang Yun-fan, et al.. Image signal enhancement based on fractional differential technologies[J]. Journal of Multimedia, 2014, 9(9): 1097-1104.
[4] Ying Y B, Wang J P, and Jiang H Y. Inspecting diameter and defect area of fruit with machine vision[J]. Transactions of the CSAE, 2002, 18(5): 216-220.
[5] 張國雄. 坐標測量技術發展方向[J]. 紅外與激光工程, 2008,37(S1): 1-5. Zhang Guo-xiong. Development orientations of coordinate measuring techniques[J]. Infrared and Laser Engineering,2008, 37(S1): 1-5.
[6] Yang C C, Marefat M M, and Ciarallo F W. Error analysis and planning accuracy for dimensional measurement in active vision inspection[J]. IEEE Transactions on Robotics and Automation, 2008, 14(3): 476-487.
[7] Kokku R and Brooksby G. Improving 3D surface measurement accuracy on metallic surfaces[J]. Society of Photo-Optical Instrumentation Engineers, 2005, 5856: 618-624.
[8] 趙博華, 王伯雄, 張金, 等. 粗糙金屬表面光條中心提取方法[J]. 光學精密工程, 2011, 19(9): 2138-2145. Zhao Bo-hua, Wand Bo-xiong, Zhang Jin, et al.. Extraction of laser stripe center on rough metal surface[J]. Optics and Precision Engineering, 2011, 19(9): 2138-2145.
[9] 易子麟, 尹東, 胡安洲, 等. 基于非局部均值濾波的SAR圖像去噪[J]. 電子與信息學報, 2012, 34(4): 950-955. Yi Zi-lin, Yin Dong, Hu An-zhou, et al.. SAR image despeckling based on non-local means filter[J]. Journal of Electronics & Information Technology, 2012, 34(4): 950-955.
[10] Kammel S and Leon F P. Deflectometric measurement of specular surfaces[J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(4): 763-769.
[11] Pu Yi-fei. Fractional differential analysis for texture of digital image[J]. Journal of Algorithms & Computational Technology,2009, 1(3): 102-107.
[12] Pu Yi-fei, Patrick Siarry, Zhou Ji-liu, et al.. Fractional partial differential equation denoising models for texture image[J]. Science China Information Sciences, 2014, 57(7): 1-19.
[13] 楊宇曉, 汪飛, 周建江, 等. 跳頻周期和跳頻間隔的最大條件熵射頻隱身設計方法[J]. 電子與信息學報, 2015, 37(4): 842-847. Yang Yu-xiao, Wang Fei, Zhou Jian-jiang, et al.. RF stealth design method for hopping cycle and hopping interval based on conditional maximum entropy[J]. Journal of Electronics & Information Technology, 2015, 37(4): 842-847.
唐瑞尹: 女,1976年生,副教授,主要研究圖像處理與光學精密檢測技術.
沈鴻海: 男,1990年生,碩士生,研究方向為圖像處理與光學精密檢測技術.
何鴻鯤: 男,1975年生,工程師,主要研究圖像處理技術.
Application of Denoising Method to Local Strong Reflection Based on Fractional Differentials
Tang Rui-yin Shen Hong-hai He Hong-kun
(College of Electrical Engineering, North China University of Science and Technology, Tangshan 063000, China)
To deal with the problem of the serious speckle or composite speckle noise in the image of the strong reflection surface, an image denoising algorithm based on fractional differential enhancement is proposed, which can highlight the granular characteristics of noise, by means of the method of connected region area to remove speckle noise and separate the effective continuous light stripe. Finally, the center of the effective light stripe is extracted with the gray gravity method. By comparison, the method can significantly improve the information entropy and the extraction accuracy of the light stripe center. The fractional differential enhancement algorithm enhance the high frequency information of the image, at the same time it effectively preserves the features of the low frequency information and more details of image texture, and the accuracy of feature extraction is significantly improved.
Image denoising; Fractional differentials; Strong reflection; Extraction of light stripe center; Entropy
The National Natural Science Foundation of China (51105273)
TP391.4
A
1009-5896(2015)12-3046-05
10.11999/JEIT150500
2015-04-30;改回日期:2015-07-27;網絡出版:2015-10-13
*通信作者:唐瑞尹 dancingbaby@126.com
國家自然科學基金(51105273)

