飽和非飽和滲流基本微分方程的推導

□楊 昱（鄭州市水利建筑勘測設計院）

0 引言

水在巖土體中沿著空隙流動的現象稱之為滲流，按照水在巖土體中的流動方式，滲流可以分為飽和流與非飽和流兩種類型。飽和滲流是指，水在巖土體流動過程中，任意一點的水頭及滲透系數不隨時間的改變。非飽和滲流是指，水在巖土體流動過程中，任意一點的運動要素隨時間而改變[1]。巖土體飽和-非飽和滲流的基本微分方程是解決巖土體滲流問題的理論基礎及計算依據。

達西定律是巖土體滲流理論的基礎，質量守恒定律及能量守能定律是一切流體運動普遍遵循的基本定律。文章首先從理論上推導了達西定律，然后根據質量守恒定律推導了連續性方程，以二者為基礎推導巖土體飽和滲流的基本微分方程，根據能量守恒定律推導了非飽和滲流的基本微分方程。

1 達西定律

達西定律是滲流理論的基本定律，最早通過實驗證實，它也可以從多孔介質中層流運動所遇到的阻力關系推導出來[2]。圖1為沿流線方向s 取得單元微分體,長為ds,斷面積為dA;作用在單元柱體上的力有:兩端的孔隙水壓力,孔隙水流的自重及水流受到顆粒孔隙道的摩阻力F。

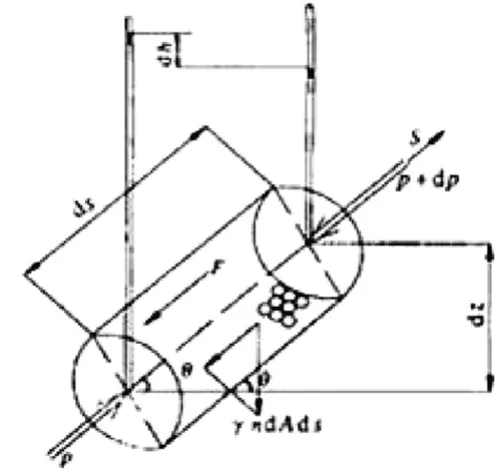
圖1 滲透水體的受力圖

沿土柱方向列出滲流的受力方程(略去水流的慣性力)：

將其代入（1）式，有：

根據斯托克斯阻力公式，單個土體顆粒所受阻力為：

式中，d 為土體顆粒直徑，v'為顆粒周圍沿滲流方向的局部平均流速；μ；λ 為一個系數，取決于臨近顆粒的影響，對于無限水體中的圓球，λ=3π。

對于總數為N 的土顆粒，引用一個球體系數β，則總阻力為：

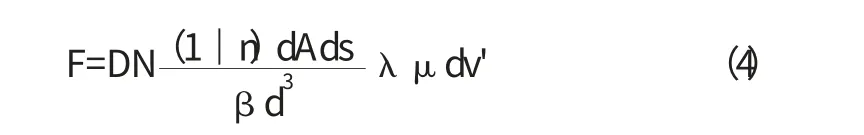
將（4）式代入（1）并考慮到斷面上的平均流速v=nv│及滲流坡降，則有：

該式即為達西定律的理論表達式。

一維飽和滲流，有：

三維飽和滲流況，有：

在直角坐標系中，以vx,vy,vz表示沿三個坐標軸方向的滲透速度分量，則有：

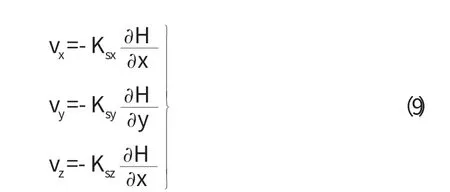
滲透速度矢量v 為：

非飽和滲流也遵循達西定律[3]。滲透系數K 是土壤含水率θ 和飽和度S 的函數K（θ）,K（S）。

在非飽和巖土體中，基質吸力表達式：

總水頭表達式：

將公式（11），(12)代入達西定律，得：

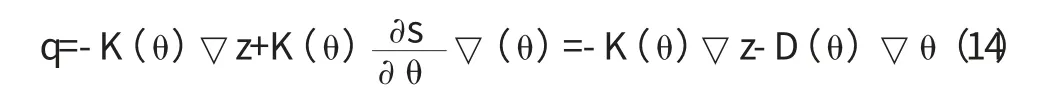
當巖土體只在x 一個方向產生非飽和滲流時，由式（13）可得：

由式（14）得：

2 連續性方程

如圖2所示，在巖土體中水分流動的空間內建立一微小的平行六面體，邊長分別為△x,△y,△z，與相應的坐標軸平行，六面體中心坐標（x，y，z）。

沿坐標軸方向的速度分量和液體密度分別用νx、νy、νz和ρ 來表示。

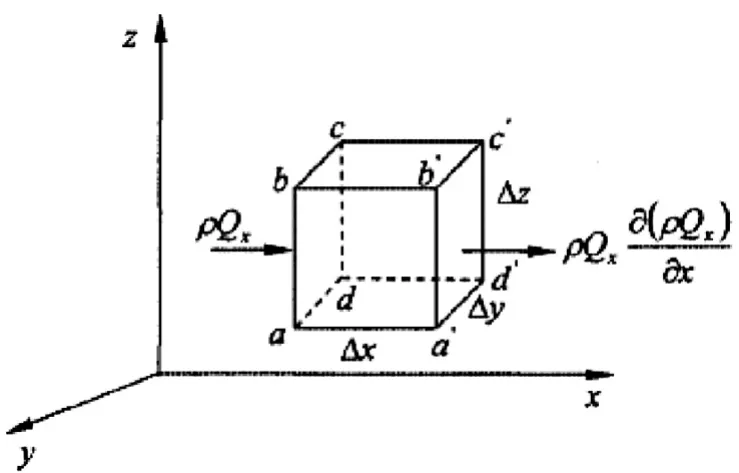
圖2 直角坐標系中的單元體圖

在△t 時間內，流入六面體左邊界面abcd 的液體質量為：

其中，Qx表示沿x 軸方向進入六面體的流量。而從六面體右邊界a'b'c'd'流出的液體質量為：

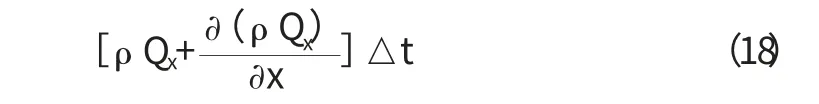
沿x 軸方向流入和流出六面體的質量差二者之差：

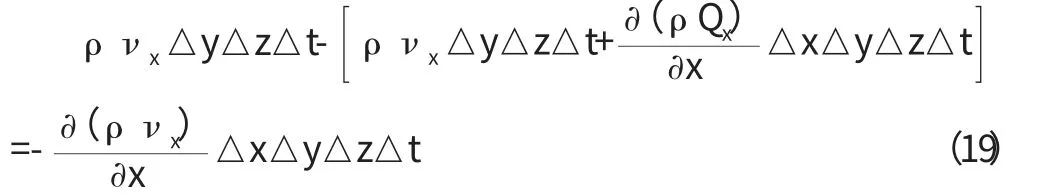
同理，沿y 軸和z 軸方向流入和流出六面體的質量差分別為：

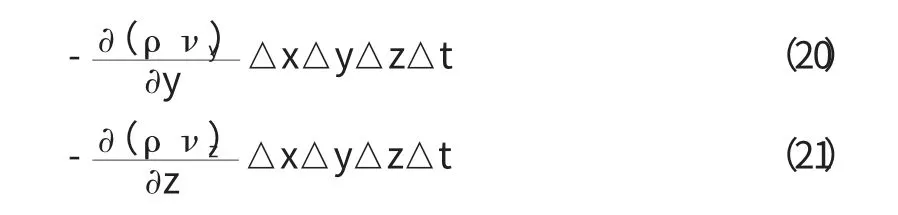
在△t 時間內流入和流出六面體單元的總的質量差為：

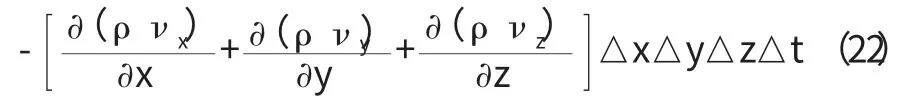
在△t 時間內，單元體內液體質量的變化量為：

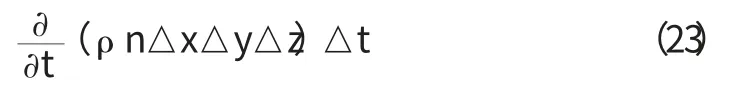
根據質量守恒定律，它應等于單元體內液體質量隨時間的變化量，即：

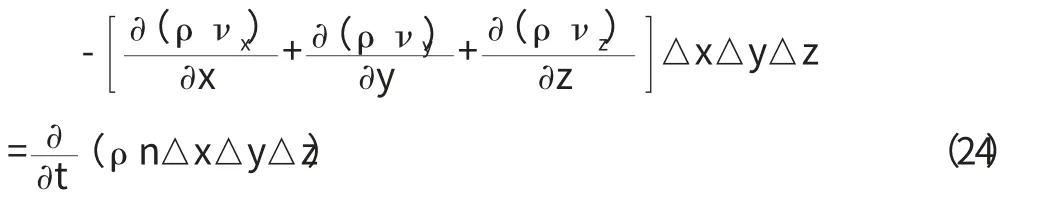
式（24）即為滲流的連續性方程。

對于不可壓縮的均質液體，密度為常數，如果含水層骨架不被壓縮，n 和△x、△y、△z 都保持不變，則有：

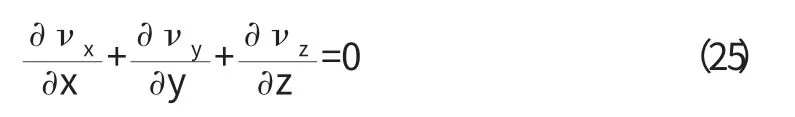
式（25）即為穩定滲流情況下的連續性方程。

3 Jacob 假定

為計算式（24）的右端項，1950年JacobBear 提出了著名的Jacob 假定[4]。假設巖土體只在垂直方向上有壓縮（或膨脹），△x、△y 視為常量，只有水的密度ρ、孔隙度n 和單元體高度△z 三個量隨壓力而變化，式（24）的右端項可以改寫為：

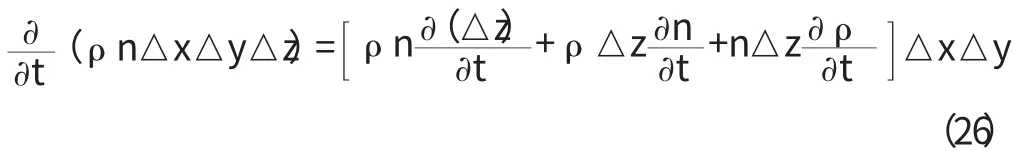
式（26）右端三項分別代表單元體骨架顆粒和孔隙體積以及流體的密度的改變速率，前兩項可表示為顆粒之間的有效應力，第三項可表示為流體壓力；就是說有效應力σ'作用于單元體，孔隙水壓力p 壓縮水體。

在多孔介質壓縮過程中，固體顆粒體積的壓縮可以略不計，即（1-n）νb=常數，則有：

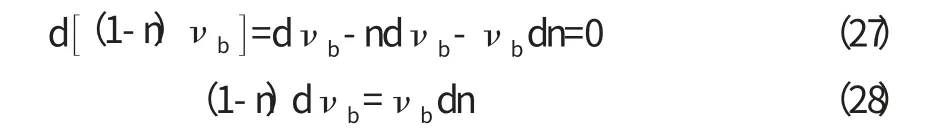
若含水層側向受限制，只在垂直方向上壓縮，即只有單元體垂直方向上長度△z 的變化，有

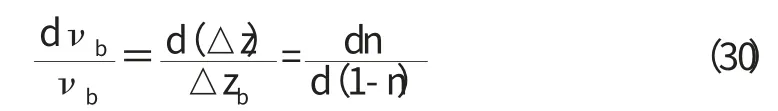
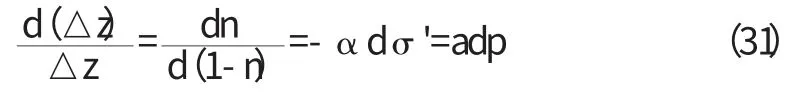
得到：

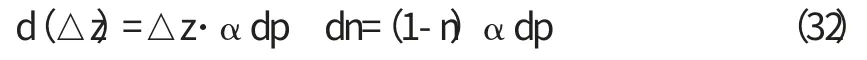
所以：

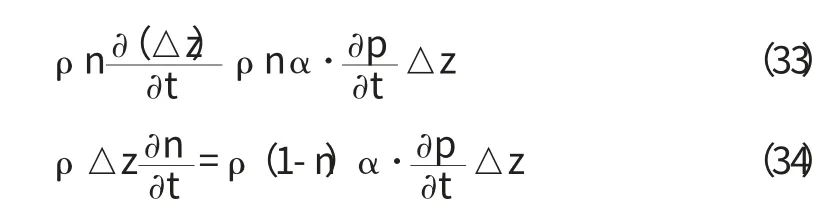
所以

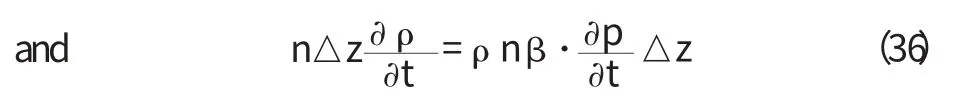
將（33）、（34）和（36）帶入（26）得：

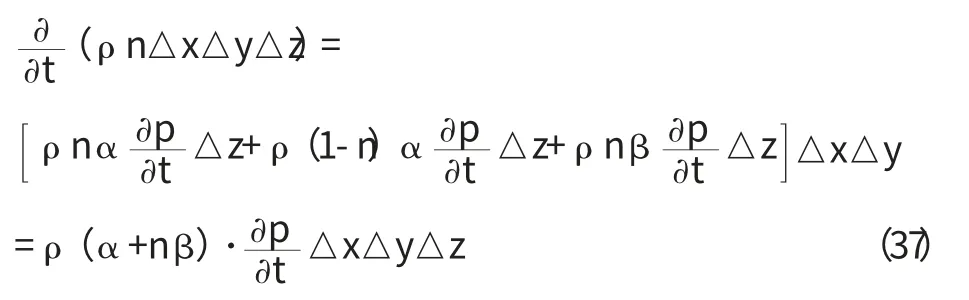
于是連續性方程（24）可化為：

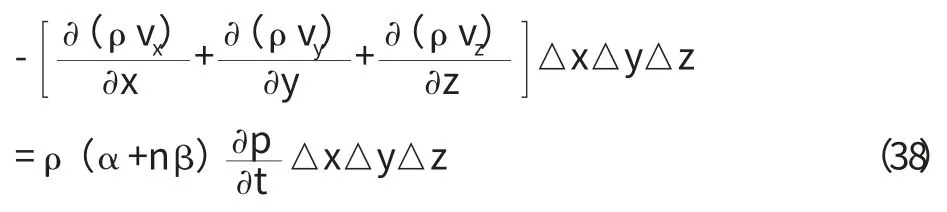
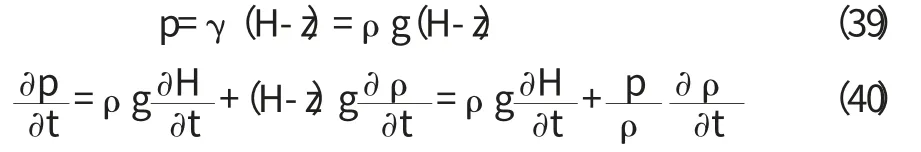
將式（39）代入上式得：

由于水的壓縮系數很小1-βp≈1，，從而有：

將式（42）代入式（38），并展開式（38）左端，得：

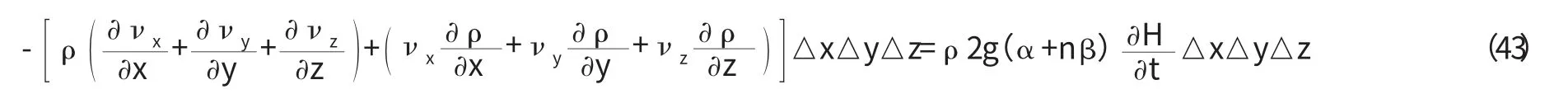
上式中，左端后一項比前一項要小得多，可以略去，故上式變為：

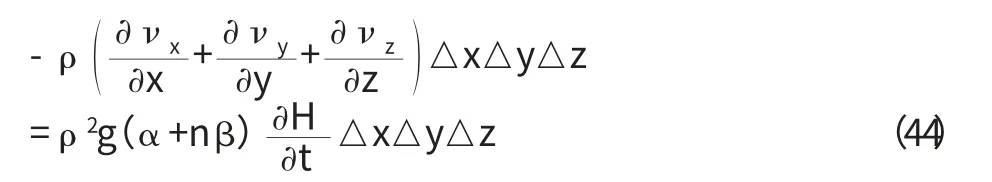
略去相同項得：

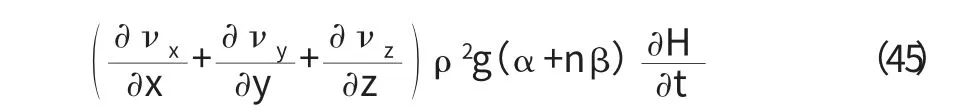
上式表示水流在運動過程中滲透速度與水頭的關系。

4 基本微分方程

根據達西定律，x、y、z 方向的滲流速度可表示為：

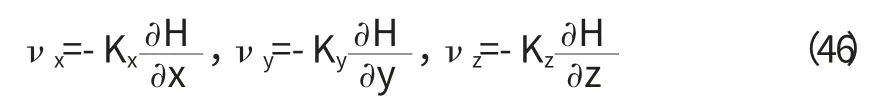
將式（46）代入式（45），并由μs=ρg（α+nβ)得：

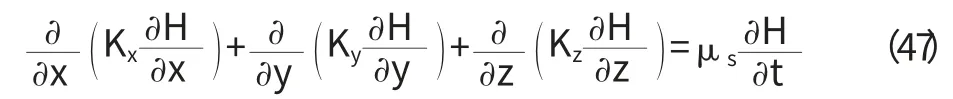
考慮抽水、注水、降雨及蒸發等情況，在基本微分方程中加入源匯項W，可得完整形式的飽和滲流微分方程[5]：

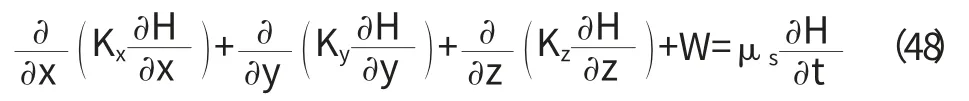
式中，W 稱為源匯項，為位置和時間的函數。

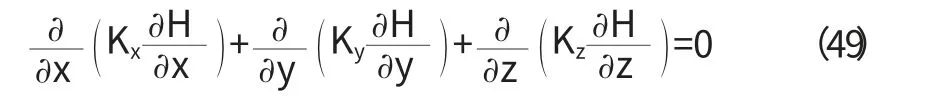
對于不考慮源匯項的均質各向同性的穩定流，有：

上式即為均質各向同性穩定流的Laplace 方程。

根據能量守恒定律[6]，在連續性方程（24）中，只要把等式右邊的孔隙度n 換成含水率θ，即可得到非飽和滲流的基本微分方程。假定非飽和介質不變形，△x△y△z 為微量，在方程兩端相同，可以約去；且在非飽和流中，水的密度ρ 變化很小，可看作常量，從而有：

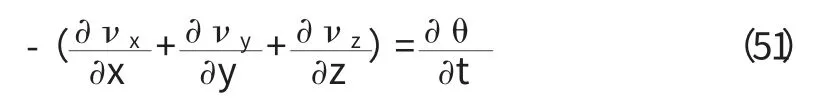
將達西定律代入可得：

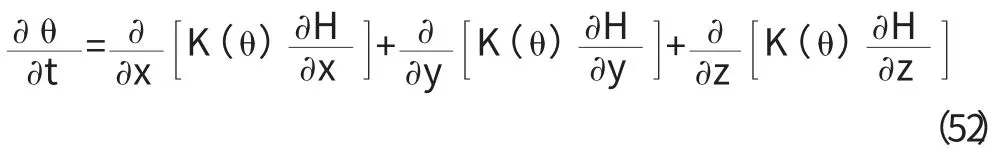
式（52）即為非飽和流的基本微分方程，稱為Richards 方程。

5 結論

針對飽和-非飽和滲流基本微分方程，以達西定律為基礎，從理論上進行了較為嚴密的，系統的推導，主要推導了以下幾個方程：

滲流的連續性方程：

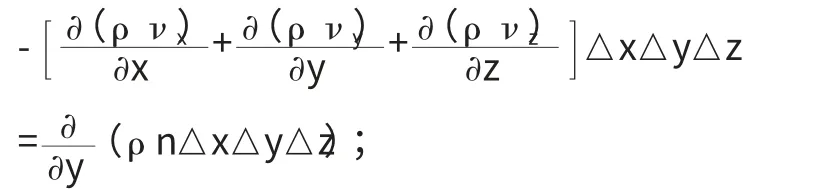
飽和流水頭與速度關系：

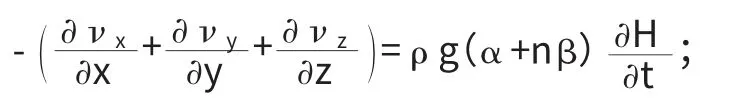
飽和滲流微分方程：

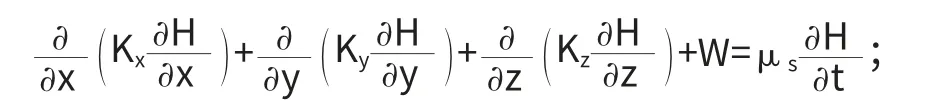
不考慮源匯項的穩定飽和滲流微分方程：

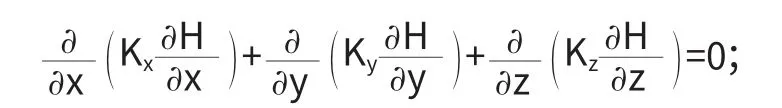
不考慮源匯項的均質各向同性的穩定飽和滲流微分方程：

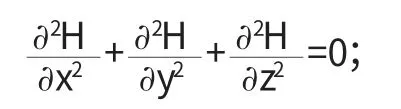
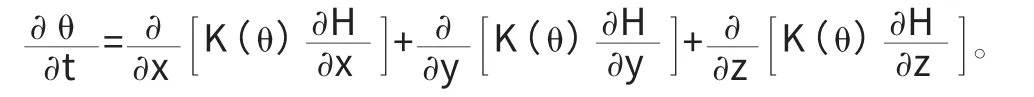
非飽和流的基本微分方程：

[1]曾鈴.降雨條件下邊坡滲流特性及穩定性研究[D].長沙理工大學,2011.

[2]苑寶軍,張玉文,姜袁.達西定律推導中的啟示在實際工程中的應用[J].常州工學院學報,2005,05:11-13+30.

[3]冉興龍,曹海東,夏斌,郭春華.Jacob 假定下含水層的儲水率及其地面沉降機理意義[J].水動力學研究與進展(A 輯),2005,03:393-399.

[4]楊永恒.滲流場與應力場耦合分析及其在尾礦壩工程中的應用[D].西安理工大學,2006.