POCKn的一類正則子半群的秩

張熹成，高榮海，b

（貴州師范大學 a.數學與計算機科學學院；b.學報編輯部，貴州 貴陽 550001）

POCKn的一類正則子半群的秩

張熹成a，高榮海a，b

（貴州師范大學 a.數學與計算機科學學院；b.學報編輯部，貴州 貴陽 550001）

設自然數n≥5,Xn=｛1,2,…,n｝,POn是Xn上的保序部分變換半群，POCKn是POn中核具有連續橫截面的元素所構成的子半群，我們得到POCKn的正則元構成的子半群秩為2n-1.

保序；連續橫截面；正則；秩

設自然數n≥5,Xn=｛1,2,…,n｝,若Xn上的一個全變換α滿足：對任意x,y∈Xn,x≤y?xα≤yα，則稱α是保序的，Xn上保序全變換（不含Xn上恒等變換）的集合記作On.設POn=On?｛｝

進而本文將考慮在POn上核具有連續橫截面的保序部分變換半群 POCKn的正則元構成子半群Reg（POCKn）的秩.

本文證明了如下主要結果：

定理設自然數n≥5，則rank（Reg（POCKn）=2n-1.

1　準備

設S是一個半群，ε∈S,若ε2=ε,則稱ε是S的一個冪等元；對于α∈S,若存在 β∈S,使得αβα=α,則稱α是S的一個正則元，S的正則元構成的集合記作Reg（S）.對于半群S,如果滿足條件：Reg（S）=S.那么稱S是正則半群.

設α∈POCKn,用im（α）表示α的象集，Ker（α）表示Xn上的一個等價關系α-1°α=｛（x,y）∈Xn×Xn:xα=yα｝,若|im（α）|=r（1≤r≤n-1），POCKn的元素有如下標準表示：其中maxA1=i,minA2=i+r-1,A1,A2?Xn，以及ai∈Xn,a1＜a2＜,...,＜ar,i=1,2,...,r.

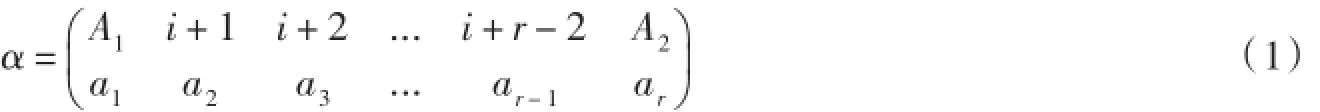
定義1［5］稱非空子鏈A?Xn是Xn的連續子鏈，若對任意k∈Xn，只要minA≤k≤maxA，則k∈A.

下面對POCKn中正則元特性進行刻劃.

命題1設α∈POCKn,||im（α）=r,4≤r≤n-1.并且有上述標準表示，則α是正則元的充要條件是：標準表示（1）中，a2＜,...,＜ar-1恰好是Xn的一個連續子鏈.

證明必要性：

α的象集是 β的核的部分連續橫截面，而 β的象集又是α的核的部分連續橫截面；若a2,...,ar-1不連續，不失一般性，不妨設a2,a3不連續，則a3=a2+x,（x≥2）,此時a2,a3一定屬于 β的兩個不相鄰單點核類，因此有a3β＞a2β+1，但由 αβα=α知，必有 a3β=i+2,a2β=i+1，即有 a3β=a2β+1，這與 a3β＞a2β+1矛盾，故a2,...,ar-1必為連續子鏈.

充分性：因為a2＜,...,＜ar-1恰好是Xn的一個連續子鏈.

POCKn中的正則元.

注1設α∈POCKn，αβα=α,由α的標準表示可知若1≤||im（α）≤3,則α都是正則元.

易見POCKn中所有正則元構成的集合構成POCKn的一個子半群，我們記作Reg（POCKn）.為了敘述上的方便，在Reg（POCKn）上引入下面的二元關系，對任意α,β∈Reg（POCKn）定義：

（α,β）∈LM?im（α）=im（β）；（α,β）∈RK?ker（α）=ker（β）；（α,β）∈J?||im（α）=||im（β）；

則LM,RK,J都是Reg（POCKn）上的等價關系，易知LM?J,RK?J.

對0≤r≤n-1,記Jr=｛α∈Re g（POCKn）:|im（α）|=r｝,Ir=｛α∈Re g（POCKn）:|im（α）|≤r｝,則J0,J1,J2,…,Jn-1恰好是Reg（POCKn）的n個J-類，I0?I1?...?In-1且恰好是Reg（POCKn）的n個理想構成的理想鏈，并且

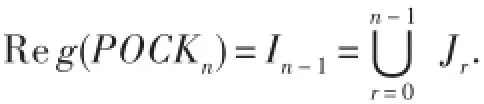
注2根據Reg（POCKn）中元素的標準表示，可知頂端J-類Jn-1中有4個R-類:

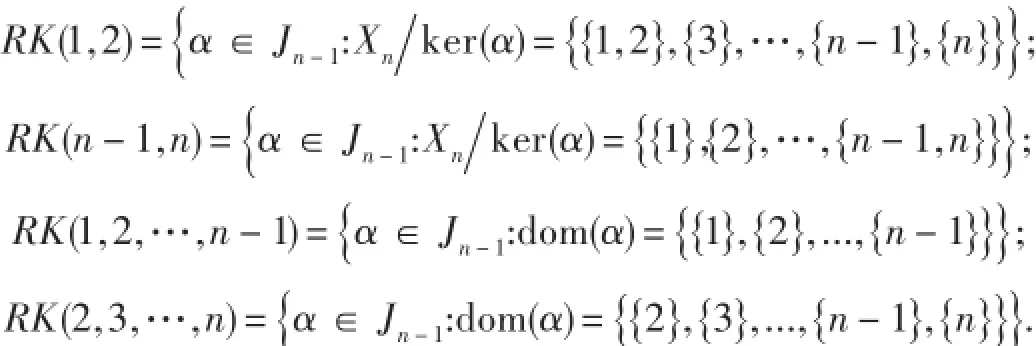
以及4個LM-類：LM（i）=｛α∈Jn-1:im（α）=Xn｛i｝｝,i=1,2,3,4.

由此可知頂端共有16個元.我們考慮Jn-1中的一個子集A=｛｝ε1,ε2,ε3,ε4分別定義為：1ε1=2,kε1=k,（k≠1）.nε2=n,kε2=k+1,（k≠n）,1ε2=1.

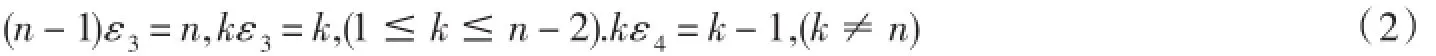
定義2設α∈POCKn,?α∈Jr（1≤r≤n-2）,若α?POCKnJr,則稱α為不可分解元.

在研究中發現Reg（POCKn）中同層J-類有兩個不可分解元而且不能相互生成，為了證明的方便，我們對Jr（1≤r≤n-2）中的兩個不可分解元分別記為：

2　主要結果及其證明

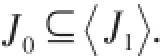
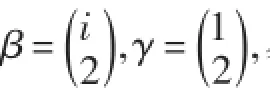
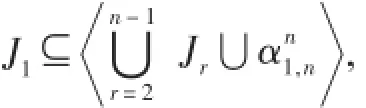
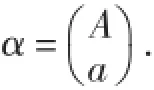
情形2當A為非單點集時.即||A＞1.

（1）當maxA=n時：

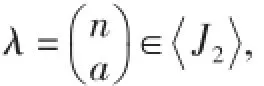
（2）當maxA≠n時，設i=maxA,t=maxA｛i｝,1＜i≤n-1.

②當a＜n時,

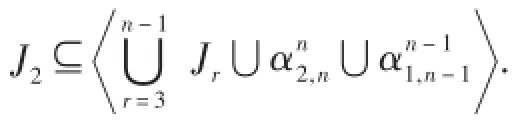
情形1當α為一一變換時：

Ⅰ.當i＞1時：

Ⅱ.當i≠n時：

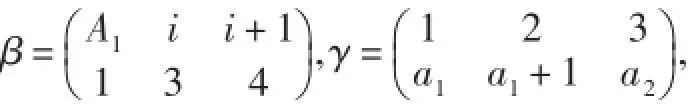
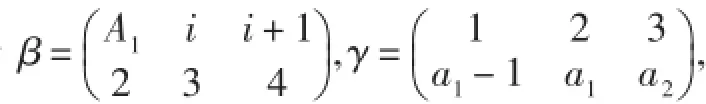
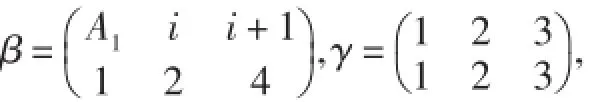
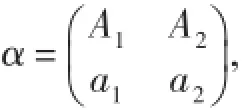
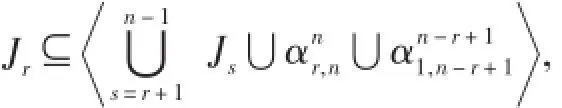
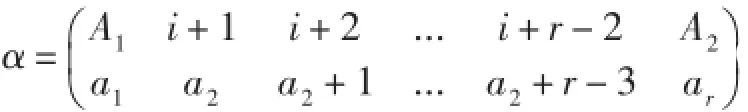
情形1當α為一一變換時：

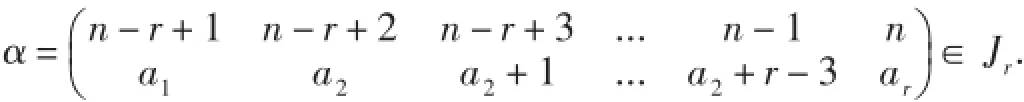
①當ar≤n-1時:

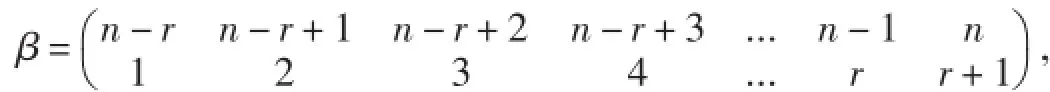
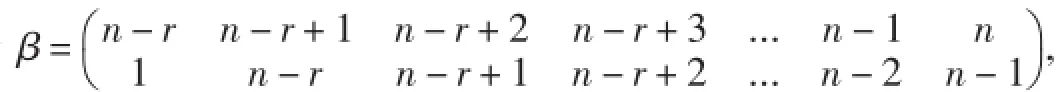
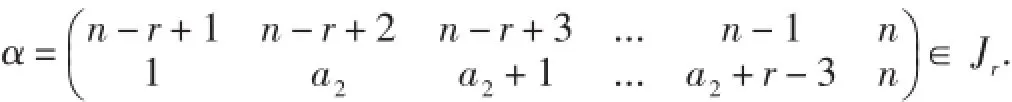
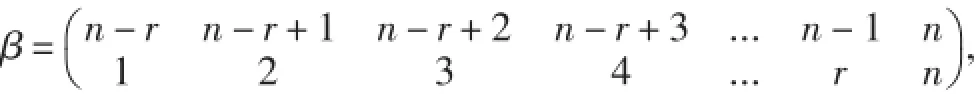
情形2當A1,A2不全為單點集時.

（1）若A1為單點集，A2為非單點集時.

①若t+1≠n時，

（2）若A1為非單點集，A2為單點集時：

①當maxA2=n時，

當t≠1時.

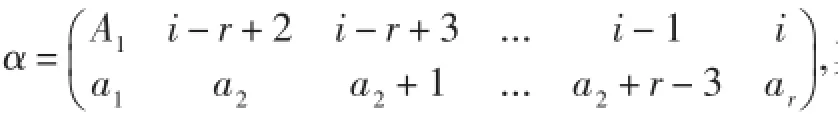
（3）若A1為非單點集，A2為非單點集時：

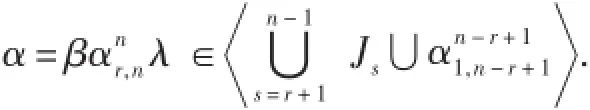
推論1自然數n≥5時，有Reg（POCKn）=Jn-1?V,其中V如前所述.

引理5設自然數n≥5,則有Jn-1?A.其中A=｛ε1,ε2,ε3,ε4｝.ε1,ε2,ε3,ε4如前文（2）所定義.

證明由于頂端J-類Jn-1中共有16個元 ε1,ε2,ε3,ε4,e1,e2,e3,e4,e5,f1,f2,f3,f4,f5,f6,f7以及 e1=ε1ε4ε3ε2. e2=ε4ε3ε2ε1,e3=ε2ε1ε4ε3,e4=ε2ε1ε4,e5=ε3ε2ε1ε4,f1=ε1ε4ε3,f2=ε1ε4,f3=ε2ε1,f4=ε3ε2ε1,f5=ε3ε2,f6=ε4ε3ε2, f7=ε4ε3.可知Jn-1?A.

由文獻［3］中引理7，易知Reg（POCKn）的任意生成集都必須覆蓋Jn-1中每個RK-類和每個LM-類，而Jn-1中共有4個LM-類和4個RK-類.因此我們得到，當自然數n≥5時,Jn-1的最少生成集的元素個數不少于4.由引理5，可得如下的推論：

推論2當自然數n≥5時，Jn-1最少生成集的個數恰好為4.

定理的證明由推論1及推論2，再由||V=2n-5,知當n≥5時，則rank（Reg（POCKn））=2n-1.

［1］Gomes G M S,Howie J M.On the ranks of certain semigroups of order-preserving transformations［J］.Semigroup Forum,1992,45 （1）:272-282.

［2］Garba G U.On the idempotent ranks of certain semigroups of order-preserving transformations［J］.Portugal Math,1994,51（2）: 185-204.

［3］高榮海，徐波.核具有連續橫截面的保序變換半群的秩［J］.西南師范大學學報：自然科學版，2013，38（4）：18-23.

［4］高榮海，徐波.半群OCKn的理想的秩［J］.蘭州大學學報：自然科學版，2013，49（3）：384-388.

［5］高榮海，喻秉均.保序壓縮變換半群的理想的極大子半群［J］.四川師范大學學報：自然科學版，2014，37（5）：643-648.

［6］徐波.正則保序壓縮變換半群的秩［J］.貴州師范大學學報：自然科學版，2012，30（3）：51-54.

［7］高榮海.關于一類純正半群的秩［J］.華南師范大學學報：自然科學版，2013，45（3）：33-35.

［8］徐波，馮榮權，高榮海.一類變換半群的秩［J］.數學的實踐與認識，2010，40（8）：222-224.

［9］高榮海，徐波.關于保序壓縮奇異變換半群的秩［J］.山東大學學報：理學版，2011，46（6）：4-7.

［10］高榮海，徐波.單調壓縮變換半群的秩［J］.數學的實踐與認識，2013，43（15）：259-262.

［11］高榮海.單調壓縮部分變換半群的秩［J］.常熟理工學院學報，2013，27（2）：35-38.

［12］Barnes G,Levi I.On idempotent ranks of semigroups of partial Transfo-rmations［J］.Semigroup Forum,2005,70（1）:81-96.

［13］Levi I.Nilpotent ranks of semigroups of partial transformations［J］.Semigroup Forum,2006,73（3）:459-476.

On the Ranks of Certain Regular Subsemigroups ofPOCKn

ZHANG Xi-chenga，GAO Rong-haia,b
（a.School of Mathematics and Computer Science；b.The Editorial Board of the Journal, Guizhou Normal University,Guiyang 550001,China）

LetPOnbe the semigroup of all the order-preserving partial transformations onXn=｛1,2,…,n｝for n≥5.LetPOCKnbe subsemigroup consisting of kernel with continuous transversal inPOn.It is shown that the rank of regular subsemigroup inPOCKnis equal to2n-1.

order-preserving；continuous transversal；regular；rank

O152.7

A

1008-2794（2015）02-0096-07

2014-10-22

通訊聯系人：高榮海，教授，碩士生導師，研究方向：半群代數理論，E-mail：gaorh1978@163.com.