嵌入技術的動態異構信息網絡的演化聚類

陳麗敏，楊靜，張健沛

(1.哈爾濱工程大學計算機科學與技術學院，黑龍江哈爾濱150001;2.牡丹江師范學院計算機科學與技術系，黑龍江牡丹江157011)

信息網絡普遍存在，如社會信息網絡、DBLP書目網絡，這些網絡由多種類型數據構成，不同類型數據之間彼此關聯，稱之為異構信息網絡。對異構信息網絡聚類分析能更好地理解網絡的隱藏結構以及每個類的數據所代表的角色［1］，而基于概率模型的異構信息網絡聚類算法［2-3］只針對具體的應用領域設計函數，不具有普遍性，且收斂性也不穩定。異構網絡的鏈接推理［4］時，往往需要最初的聚類劃分更精確一些，而傳統的高階異構聚類算法［5-6］復雜度太高不適合異構信息網絡。異構信息網絡經常是動態的而非靜態的，動態同構數據的演化聚類［7］的研究已經做了很多，而動態的異構信息網絡的演化聚類分析，目前只有ENetClus［8］算法，該算法沒有關注聚類質量，更側重跟蹤類的變化及分析類的推進、形成與消失。Khoa［9］使用近似 commute time嵌入聚類同構數據集，取得了很好的效果。受該思想啟發，本文從相容二部圖的角度提出一種基于嵌入技術的動態異構信息網絡的演化聚類算法，具有較高的聚類質量，且計算速度也比較快。

1 時間平滑二部圖

定義 1:給定G=＜V，E，W＞，V=X0∪X1，其中X0與X1為2個不同類型的數據集。若?〈xi，xj〉∈E，則xi∈X0且xj∈X1，稱G為二部圖。

r(xi，xj)表示二部圖G的結點xi與xj的關系，若結點xi與xj有關系，則結點xi與xj之間有邊存在，否則無邊存在。

給定t時刻的二部圖Gt，?xi，xj∈Gt。使用代價函數時間平滑Gt兩結點的關系:

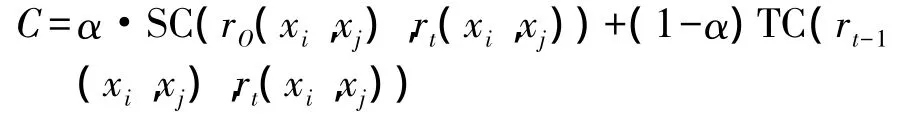
式中:rt(xi，xj)表示t時刻結點xi與xj的時間平滑的關系，rO(xi，xj)表示t時刻二部圖兩結點的原始關系，即沒有時間平滑的關系。rt－1(xi，xj)表示先前時間結點xi與xj之間的關系。SC(·)為快照代價函數，表示t時刻rt(xi，xj)與rO(xi，xj)的相似度。TC()為時間代價函數，表示t時刻rt(xi，xj)與rt－1(xi，xj)的相似度。

函數SC()和TC()可選擇多種衡量指標。取SC()=，使cost最小的rt(xi，xj)就是最佳關系，則兩結點最佳的關系為

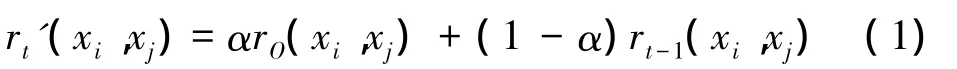
例如，t時刻DBLP書目網絡的papers與authors構成一個二部圖G，G中只有不同類型的結點之間存在關系。t時刻的G中，先前時間的papers已經全部更換，但先前時間的authors會保留在t時刻的二部圖中，因此t時刻的二部圖G，僅使用異構數據的關系無法體現先前時間authors之間的聯系。而先前時間authors之間的聯系影響著t時刻papers的劃分。所以需要表達先前時間所有結點間的關系。cij表示二部圖結點i，j的commute time距離，cij能夠表達二部圖的所有結點間的關系。cij是2個結點間所有路徑的平均值，故cij能夠表達一段時間兩結點的關系。令ct(xi，xj)表示t時刻及先前時間結點xi與xj的 commute time 距離。令rt－1(xi，xj)=ct－1(xi，xj)，rO(xi，xj)是t時刻二部圖Gt中兩結點的原始關系。由式(1)獲得t時刻時間平滑二部圖，若rt'(xi，xj)≠0，則兩結點之間存在邊，否則無邊。rt'(xi，xj)≠0的數目就是的邊的數目，中2個相同類型的結點之間也可能存在邊。充分體現了t時刻及先前時間所有結點間的關系。

式(1)只計算t時刻屬于的結點間的關系。先前時間結點的關系會導致不夠稀疏，通過計算Gt中也屬于的結點的k近鄰，可構造稀疏的時間平滑二部圖。由2.2節可快速計算的近似commute time嵌入，而由嵌入可計算任意兩結點的ct(xi，xj)，因此每次只要存儲t時刻近似commute time嵌入即可。

2 時間平滑二部圖的近似commute time嵌入

2.1 時間平滑二部圖的commute time嵌入

設G'是加權無向圖，L是G'的Laplacian矩陣，L+是L的偽逆矩陣，則

性質 1［10］:cij=Gvol'(ei－ej)TL+(ei－ej)

其中Gvol'是G'的權重總和，即Gvol'=∑wij;wij為G'的結點i、j構成的邊的權重;ei是第i個元素為1的單位列向量，即

設Λ與Φ分別是時間平滑二部圖的Laplacian矩陣L的特征值構成的對角矩陣及特征值對應的特征向量矩陣，特征值λ1≤λ2≤…≤λn。L+是的矩陣L的偽逆矩陣，則由性質1，的任意兩結點i，j的cij為

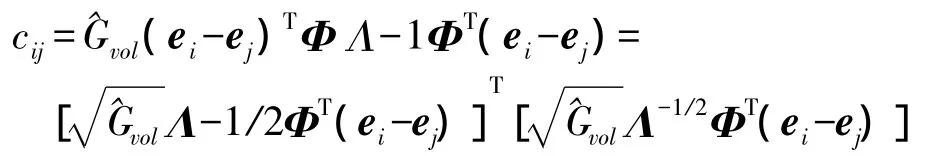
則cij是空間第i列向量與第j列向量的歐式距離的平方，稱為時間平滑二部圖的commute time嵌入［11］。

直接計算ψ需花費O(n3)時間分解特征矩陣。設有n個結點s條邊，定向的邊，令

則 Bs×n是一個有向邊－點入射矩陣。令是由邊的權值構成的對角矩陣，則的Laplacian矩陣 L=BTB［11］。

2.2 時間平滑二部圖的近似commute time嵌入

其中，Qkr×s是行向量獨立同分布的隨機矩陣，

但計算Y，涉及L+，直接計算 L+復雜度過高。根據文獻［12］方法，可分解計算Y。令()，則 Y=θL+，等價于計算 YL=θ。通過矩陣θ的每個行向量θi計算方程組yiL=θi，其中yi是矩陣Y的行向量。使用STSolve求解程序［13］能夠線性時間計算出yiL=θi每個近似的，由于，則

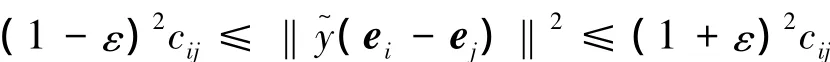
設Gt對應的鄰接矩陣為 Wn0×n1，t時刻的近似commute time嵌入的算法如下:

算法1 ApCte(approximate commute time embedding)

輸入:t時刻二部圖Gt的Wn0×n1;

輸出:的近似commute time嵌入;

步驟:

1)查找Gt中屬于的結點，由指示數據計算這些結點的k近鄰，由式(1)計算的鄰接矩陣;

4)采用 STSolve 方法［13］計算 YL=θ 的每個;

5)輸出的嵌入。

數據集X0與X1的樣本映射到了一個共同的子空間。的前n0個列向量指示數據集X0，后n1個列向量指示數據集X0。設Gt中屬于的結點數為nt，nt＜n，算法 1 的 1)步采用kd樹構造Gt中屬于的結點的k近鄰需要O(ntlnnt)時間。是稀疏圖，鄰接矩陣有s個非零元素，則2)步計算B與及L的時間為O(2s)+O(s)+O(n)。因為稀疏矩陣B有2s個非零元素，對角矩陣有s個非零元素，故3)步計算 θ的時間為O(2skr+s)。4)步用STSolve 方法［13］計算的時間為(skr)。則算法 1的時間復雜度僅為(ntlnnt+4s+n+3skr)。

3 基于近似commute time嵌入的異構信息網絡的演化聚類

3.1 模型的組成

定義2 給定一個由M+1種類型的數據集χ=構成的信息網絡G=＜V，E，W＞，如果?e=〈xi，xj〉∈E，那么xi∈X0且xj∈Xmm≠0，則G稱為星型模式的異構信息網絡，X0稱為目標類型，Xm(m≠0)稱為屬性類型。

給定一個由M+1種類型的數據集構成的星型模式的異構信息網絡，其中是Xm的對象數目，X0為目標數據集為屬性數據集。W(0m)∈Rn0×nm表示X0與Xm之間的關系，其中，元素表示X0的樣本與Xm的樣本的關系。如果與存在關系，則與有邊存在，邊的權重為，否則無邊該信息網絡包含M個關系矩陣

t時刻目標數據集X0與屬性數據集Xm構成一個二部圖，由式(1)可計算t時刻時間平滑二部圖，設的鄰接矩陣為。由 2.2節，可計算的近似commute time嵌入Y(0m)=，其中前n0個列向量指示目標數據集X0，表示為，稱之為指示子集，后nm個列向量指示屬性數據集Xm，表示為Y(m)。稱指示X0第i個對象的數據為指示數據，1≤i≤n0.的指示數據與X0的對象存在一一對應的關系。M個二部圖對應M個近似commute time嵌入，則目標數據集X0被M個指示子集所指示，X0的每個對象被M個指示數據所指示。

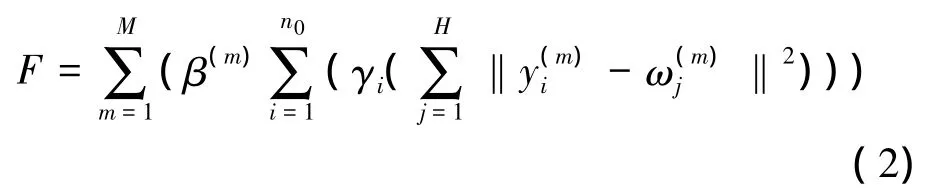
設X0劃分為H個類，β(m)是矩陣的權重，其中數據屬于M個類，這M個類分別位于不同的指示子集，這M個類設置相同的類標號。令

從相容的角度，式(2)的目標函數F取得最小值，則目標數據集X0聚類達到最佳。顯然，式(2)的全局最優解是NP難問題。

3.2 快速算法的推理

3.2.1 類標號設置

在目標數據集X0中隨機選擇H個對象，指示這H個對象的指示數據在各自的指示子集中作為H個類的初始中心點，指示同一個對象的中心點，令其所在類的標號一致，則其他指示同一個對象的指示數據或者都屬于第j個類，或者都不屬于第j個類，1≤j≤H。

3.2.2 加權距離總和

X0的一個對象被M個指示數據所指示，這M個指示數據到各自指示子集的類的中心點的距離都影響著這個對象所屬類的分配。設qi∈X0，指示qi，則權重距離總和決定了qi所屬的類。即

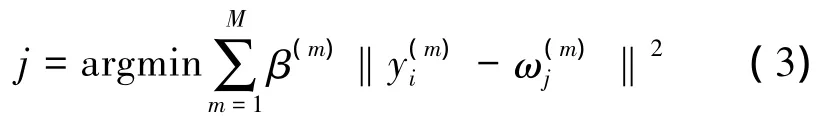
式中:j是qi所屬類的標號，也是所屬類的標號。

3.2.3F的極小值

式(2)的F也可以表示為指示同一個對象的指示

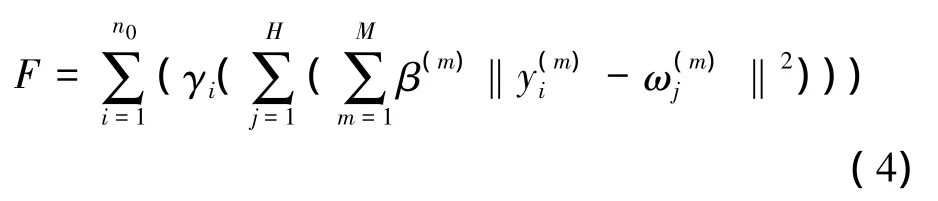
給定M個指示子集的類的初始中心點，首先由式(3)劃分指示子集的類，此時令F=F0;的類的中心點不變，然后計算的每個類的新中心點，新中心點取值所在類的所有指示數據的平均值，令

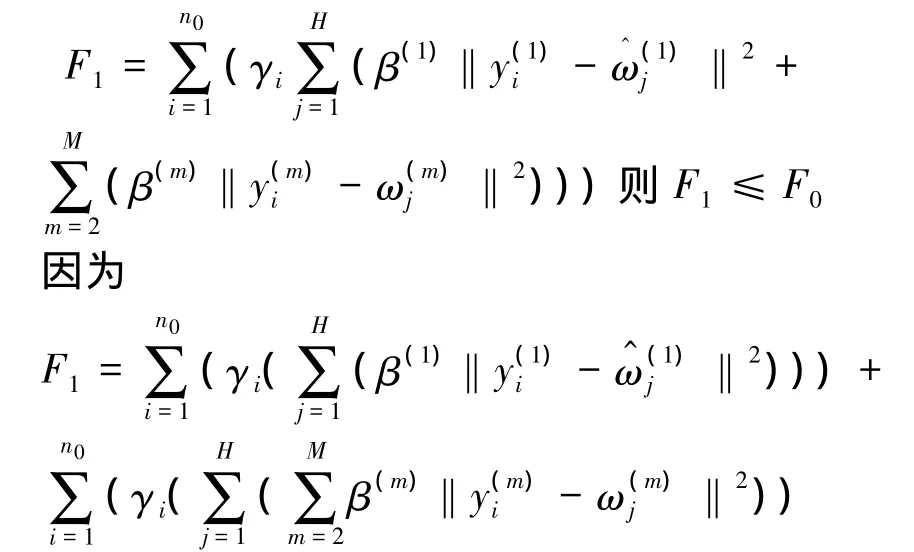
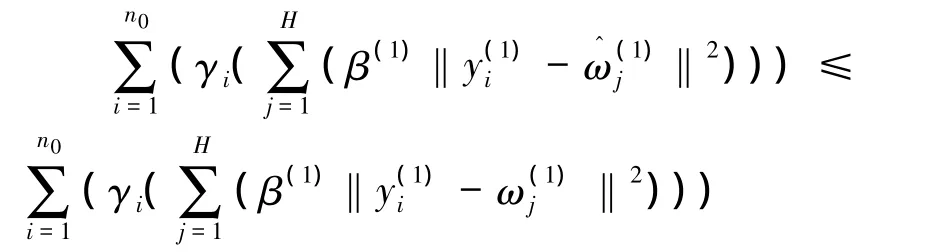
故F1≤F0。

而當的類替換了新的中心點的中心點不變，由式(3)重新劃分類，此時令F=F2，則有F2≤F1。

算法2 EClu-pACte(evolutionary clustering algorithm based on approximate commute time embedding for heterogeneous information network)

輸 入:t時 刻的，聚類數H;

輸出:t時刻目標數據集X0的類;

步驟:

1)form=1∶Mdo

{①由算法1計算的嵌入Y(0m);

②確定指示X0的指示子集;}

3)do

{form=1∶Mdo

{①計算式(3)劃分的H個類;

②重新確定每個類的新的中心點，并建立類標號;

}while式(4)收斂;

4)輸出目標數據集X0的類。

4 實驗

4.1 實驗數據

從DBLP信息網絡選取真實數據建立實驗數據集，取 venues、authors、papers和 terms建立書目網絡。選取4個學術區域建立小數據集Ssmall，這4個區域包括 database、data mining、information retrieval和machine learning。每個區域取5個有代表性的conference，共20個會議，20個會議的所有authors、papers及出現在論文題目中的所有terms。papers為目標數據集，venues、authors和terms為屬性數據集，建立一個星型模式的異構信息網絡。本文使用Ssmall分析kr對聚類準確率的影響。

對1993－2008年上述4個學術區域的20個會議的所有authors、papers及出現在論文題目中的所有terms，分析目標數據集papers的演化情況。

本文算法EClu-pACte的所有實驗均采用文獻［13］的一種近乎線性時間的求解程序計算的嵌入數據集，該方法用于對角占優矩陣。所有算法均在MATLAB環境中實現。

4.2 關系矩陣的確定

X0表示目標數據集 papers，X1、X2與X3分別表示屬性數據集 authors，venues與 terms。則X0與的原始關系為的元素為

4.3 參數kr取值分析

選取小數據集Ssmall，對于給定的kr，取u=50，α=1，參數kr的變化對papers聚類質量的影響，如圖1所示。實驗說明當kr＞50時準確率曲線已經趨于平滑，取kr=60很適合，則其他實驗也取kr=60。

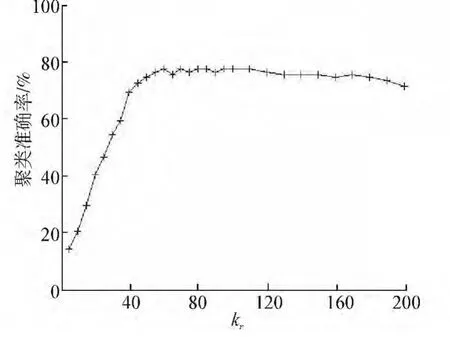
圖1 kr對聚類準確率的影響Fig.1 The influence of kron clustering accuracy

4.4 參數α取值分析

參數α是用來平衡快照質量與歷史質量的。本實驗的目標數據集papers在不同的時間點(年份)是不同的，沒有重復的，papers不存在連續性，但屬性數據集存在連續性。屬性數據集的連續性影響t時刻目標數據集papers的劃分，使得t時刻的papers與先前時間的papers存在著關聯。本次實驗取k=7，α的取值對聚類準確率的影響如圖2所示，其中圖2的聚類準確率取每個時刻(1994－2008)共計15個聚類準確率的平均值。說明α=0.8聚類質量最好。

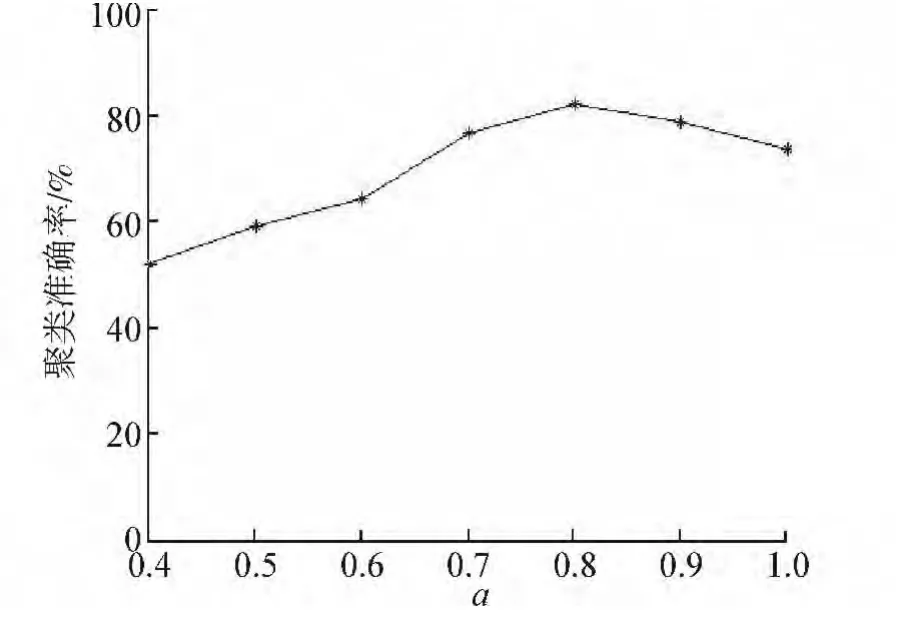
圖2 α對聚類準確率的影響Fig.2 The influence of α on clustering accuracy

4.5 計算速度分析

劃分1994年的papers，比較α取不同值時不同算法的計算速度。如表1所示，當α=1時，t時刻的二部圖沒有時間平滑，異構信息網絡是稀疏的，故計算速度很快，與ENetClus算法計算速度幾乎一致。當0＜α＜1時，計算速度略有下降，原因是需要計算中屬于的結點的k近鄰，以構造稀疏的時間平滑的二部圖。但采用kd樹構造Gt中屬于的結點的k近鄰僅需要O(ntlnnt)時間。實驗的目標數據集是papers，中的papers肯定不會出現在t時刻的中，故每次只需存儲指示屬性數據集authors、venues和terms指示子集即可，因此計算速度相對還是比較快的。

表1 計算速度比較Table 1 Comparison of computing speed s

4.6 準確率分析

ENetClus算法取文獻［8］的最佳參數，本文算法取α=0.8，其他參數同上述實驗。準確率比較如圖3所示，本文算法的聚類質量要明顯好于ENet-Clus算法。與ENetClus算法相比，本文算法能夠比較真實地反映在t時刻及先前時間數據對象的關系。若t時刻的數據對象與先前的數據對象不存在任何關系，本文算法能夠真實地反映出來。而ENetClus算法是從類的角度時間平滑，而不管前后兩個時刻數據是否確實存在關系，因此比較粗糙。若前后時刻數據存在關系，ENetClus能大致反映其關系，否則ENetClus反映的是錯誤的關系。而且基于概率模型的ENetClus算法受應用領域限制，通用性不強。

圖3 演化聚類準確率比較Fig.3 Comparison of evolutionary clustering accuracy

5 結論

通過理論分析及實驗驗證說明:

1)本文采用時間平滑二部圖充分反映了某時刻及先前時間結點間的關系，聚類質量高于以往的算法;

2)實驗的運行時間說明利用稀疏性，采用線性時間求解程序加快了計算速度;

3)本文算法通用性強，適合于任何的星型模式的異構信息網絡，不受異構信息網絡的應用領域所限制。但本文算法參數較多，每個時間平滑二部圖的關系的權重都需要人為確定，如何自動選取最佳的關系權重，還需進一步研究。

［1］SUN Yizhou，HAN Jiawei.Mining heterogeneous information networks:principles and methodologies［J］.Synthesis Lectures on Data Mining and Knowledge Discovery，2012，3(2):1-159.

［2］SUN Yizhou，YU Yintao，HAN Jiawei.Rankclus:rankingbased clustering of heterogeneous information networks with star network schema［C］//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，ACM，2009:797-806.

［3］WANG R，Shi C ，PHILIP S Y，WU B.Integrating clustering and ranking on hybrid heterogeneous information network［M］.Berlin Advances in Knowledge Discovery and Data Mining.2013:583-594.

［4］AGGARWAL C，XIE Y，PHILIP S Y，On dynamic link inference in heterogeneous networks［C］//SDM.2013:415-426.

［5］GAO Bin，LIU Tieyan，MA Weiying.Star-structured highorder heterogeous data co-clustering based on cosistent information theory［C］//ICDM＇06.Hong Kong，China，2006:880-884.

［6］LONG Bo，ZHANG Zhongfei，WU Xiaoyun，et al.Spectral clustering for multi-type relational data［C］//Proceedings of the 23rd International Conference on Machine Learning，ACM.2006:585-592.

［7］AGGARWAL C，SUBBIAN K.Evolutionary network analysis:a survey［J］.ACM Computing Surveys(CSUR)，2014，47(1):10.

［8］GUPTA M，AGGARWAL C，HAN J，et al.Evolutionary clustering and analysis of bibliographic networks［C］//Advances in Social Networks Analysis and Mining(ASONAM).Kaohsiung，Taiwan，2011:63-70.

［9］KHOA N L D，CHAWLA S.Large scale spectral clustering using resistance distance and Spielman-Teng solvers［J］.Discovery Science，2012:7-21.

［10］QIU H，HANCOCK E R.Clustering and embedding using commute times［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(11):1873-1890.

［11］SPIELMAN D A，SRIVASTAVA N，Graph sparsi fi cation by effective resistances［J］.SIAM Journal on Computing，2011，40(6):1913-1926.

［12］SPIELMAN D A，TENG Shanghua.Nearly-linear time algorithms for preconditioning and solving symmetric，diagonally dominant linear systems［J］.SIAM Journal on Matrix Analysis and Applications，2014，35(3):835-885.

［13］KOUTIS I，MILLER G L，TOLLIVER D.Combinatorial preconditioners and multilevel solvers for problems in computer vision and image processing［J］.Computer Vision and Image Understanding，2011，115(12):1638-1646.