不確定載荷下剛架體結構穩健優化設計

楊繼超，戴宗妙

(1.哈爾濱工程大學機電工程學院，黑龍江哈爾濱150001;2.中國船舶重工集團公司第七一三研究所，河南鄭州450015)

優化設計是指在特定約束條件下，獲得結構某種性能指標(如體積、質量或擾度等)最優。傳統的優化設計，往往建立在確定性模型基礎上，沒有考慮變量參數實際值與名義值存在的差異，得到的優化解位于可行域邊界。當實際工程中變量參數(如載荷)發生擾動時，理論最優解很可能落在不可行區域，給設計帶來潛在風險。針對工程設計中不確定性，國內外學者提出許多設計理論和方法。其中穩健設計基本思想是在不消除不確定性源的前提下，提高產品對不確定因素抵抗力［1］。結構穩健優化一個難點是對不確定性力的分析及對優化過程影響，即建立不確定性優化模型。

目前，基于概率不確定模型應用比較成熟。文獻［2-4］通過構造約束和目標函數靈敏度分析，進行穩健優化設計;文獻［5］采用Kriging模型，建立以目標性能指標均值和方差為優化目的優化模型;文獻［6］將穩健優化問題轉化成多目標優化問題，對結構進行優化設計;為了提高計算效率，文獻［7］基于隨機響應量前四階矩建立穩健優化設計模型。基于概率模型方法需要大量樣本數據估算參數的不確定度或分布函數，而這些數據在實際工程中往往很難實現。然而獲得不確定因素的邊界，是相對容易的。非概率方法就是根據不確定參數未知但有界的特點進行建模。文獻［8-10］提出了基于凸集理論的非概率不確定模型分析方法，對結構進行穩健性分析。文獻［11］在非概率凸模型可靠性約束下，通過超橢球域界定不確定參量，進行結構優化設計。文獻［12-13］運用區間模型對不確定性參數進行非概率性描述，建立結構優化和設計方法。目前，在集合理論凸模型中，大多方法都是求解結構響應上下界解析解的近似值［14］;對于復雜的結構，區間模型計算量往往非常大，計算效率低下甚至無法實行。

20世紀90年代，Ben-Haim提出非概率Information-Gap(I-G)理論描述不確定性模型，并以系統承受最大不確定性波動作為評價結構穩健性的指標。文獻［15-16］給出了非概率的I-G模型處理不確定性的理論方法，文獻［17-18］基于I-G理論，對地下結構在非確定因素影響下結構的穩健性進行分析。為此，本文針對剛架體結構承受不確定載荷特點，引入I-G理論，建立結構非概率穩健性模型，并結合優化設計方法，對剛架體結構進行穩健性優化設計，提高對不確定因素的抵抗能力。

1 不確定載荷I-G模型

1.1 剛架體應力約束方程

在實際工程中，剛架體結構通常會受到不確定載荷作用，且結構需要滿足最基本應力約束要求。令一個線彈性的三維剛架體結構自由度為n，則系統平衡方程為

式中:u∈Rn和f∈Rn分別表示節點的位移和外載荷矢量，K∈Sn為剛度矩陣。對于有m個桿件的剛架體結構，桿截面積a=(ai)∈Rm，則K可以寫成如下形式:

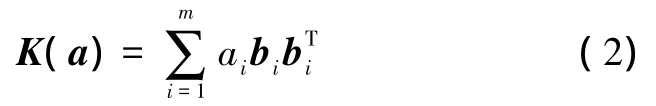
式中:b=(bij)∈Rn是常向量。則由上述關系式，應力約束方程為

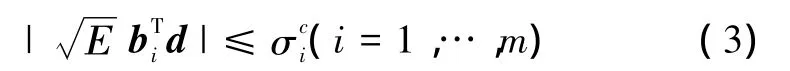
式中:E表示彈性模量，表示第i桿許用應力。根據位移表示約束方程，則有

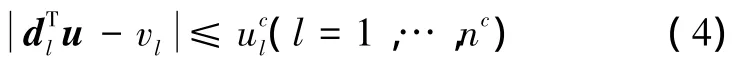
式中:dl∈R，常量vl∈R。為了保證剛架體結構的安全穩定，桿件必須滿足式(3)或式(4)。當上述約束關系式滿足時，不確定變量允許一定的變化幅度。這里通過穩健函數來度量，它與影響剛度矩陣的桿截面積和不確定程度相關。

1.2 不確定性因素I-G分析

I-G模型是由凸集理論基礎發展而來。根據I-G理論，不確定度是采用已知信息與未知信息的偏離程度或斷缺狀態描述。由于外在環境的不可控性以及所需解決問題信息掌握貧乏，結合剛架體結構特點，建立不確定性影響因素的I-G模型。不確定參數不確定性程度可表達為［17］

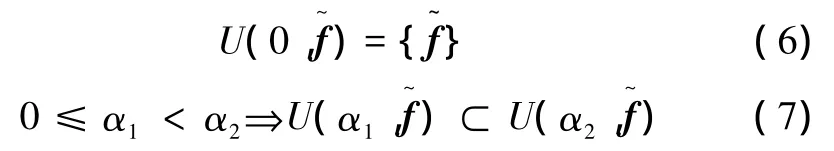
式(6)表明，當不考慮載荷不確定性(α=0)時，名義載荷即為實際載荷f，I-G模型退化成確定性模型。式(7)表明，不確定參數α決定不確定因素真實值和名義值之間的偏離程度，當α小時，和f越接近;反之偏離程度大。相比較其他非概率模型，如固定區間模型或凸集模型，I-G模型U(α，)的嵌套凸集特性能更好反應不確定性載荷的動態變化。

1.3 基于I-G模型穩健函數構造

穩健性反映結構對不確定性因素的抵抗程度，如果結構能夠允許較大不確定性變化而不失效，就認為該結構穩健強。上一節，建立了不確定載荷的I-G模型，定義參數α表示不確定性變化幅度。

在滿足約束條件式(3)或(4)的前提下，結合I-G理論，剛架體結構系統的平衡方程(1)所有可能解集可表示成

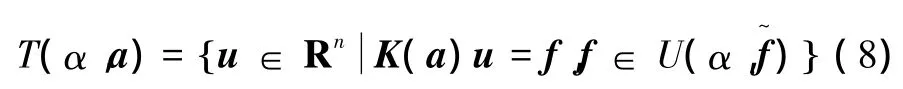
結合式(4)、(8)，式(9)的最優規劃問題可表示為

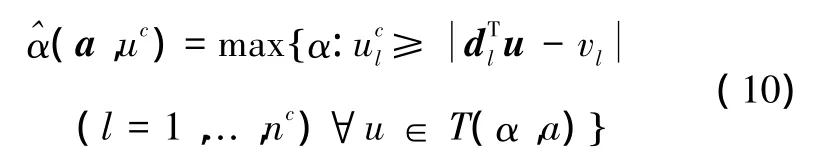
式(10)即為穩健函數。對于兩組不同剛架體截面積向量a1∈Rn和a2∈Rn，如果則a1比a2穩健。

2 結構穩健優化模型

2.1 一般優化模型形式

傳統的確定性問題數學優化模型可以表示為

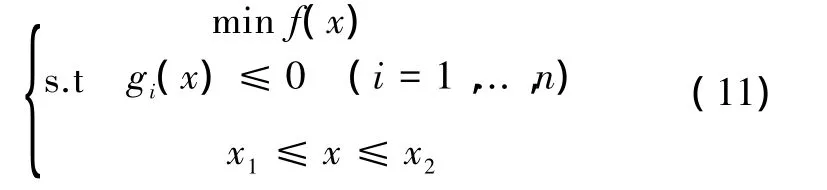
式中:f(x)為優化模型的目標函數，x優化設計變量;gi(x)和n分別為約束條件以及約束條件數量;x1、x2為設計變量的取值范圍。

當存在不確定因素時，結構穩健優化不但要考慮不確定因素對優化模型的影響，還要考慮目標函數的穩健性，即能抵御不確定因素的影響。結合上一節的分析，注意到穩健函數值大的結構更為強健。基于優化理論，建立穩健函數最大化問題的優化模型。考慮結構體積(質量)約束條件，橫截面向量a應該滿足:

式中:li＞0 表示第i個桿長，為體積上限。對限定的位移uc和，應力約束下魯棒函數最大化問題優化模型可以寫為

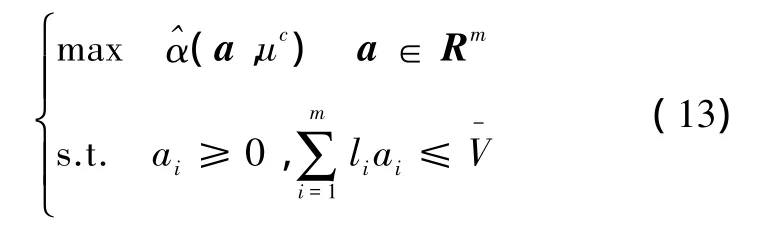
優化目標為穩健性函數最優，即結構抵抗不確定性載荷最大化。

2.2 半定規劃模型

上述過程中，基于I-G模型處理不確定載荷，則載荷集中包含無窮多載荷，常規方法很難對上式進行求解。因此通過半定規劃對穩健優化模型進行重新構造。傳統半定規劃的數學形式為［14］

式中 c，x∈Rn，Fi(i=0，…，n)為n階常對稱矩陣，x 為設計變量，矩陣F(x)?0為正定。

結合本文優化模型式(13)，令F?Rn表示滿足上述應力約束(4)的力集合:

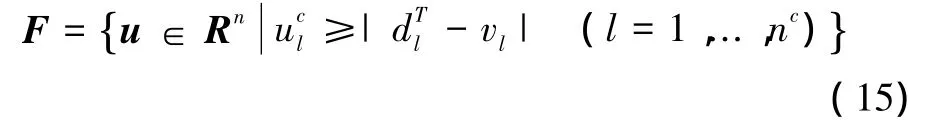
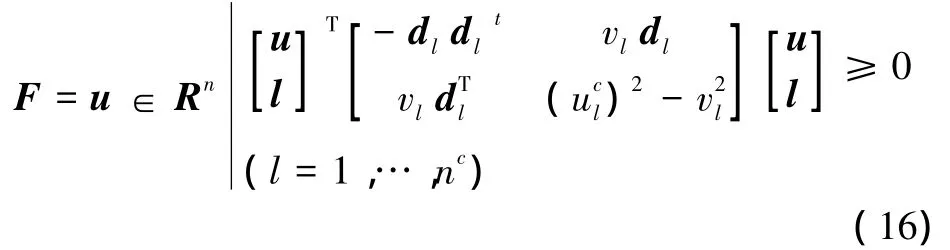
進行如下定義:

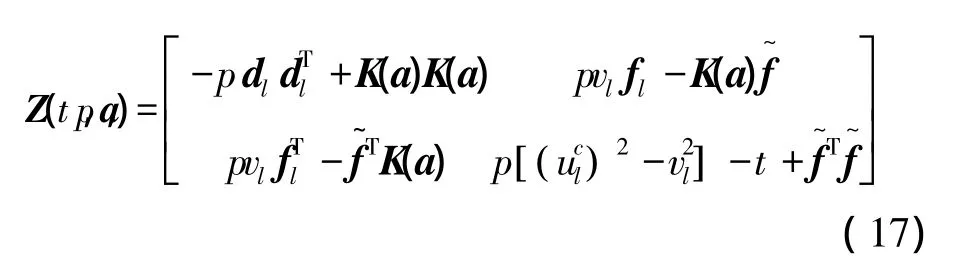
其中，p，t∈R，a∈Rm。將新參數(t，p)引入穩健函數(a，uc)中，則可以得到:

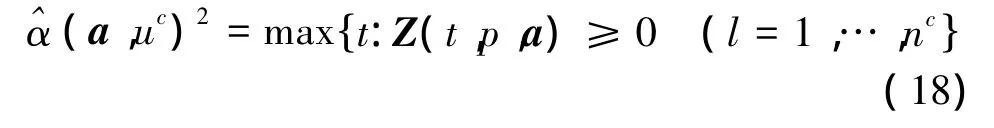
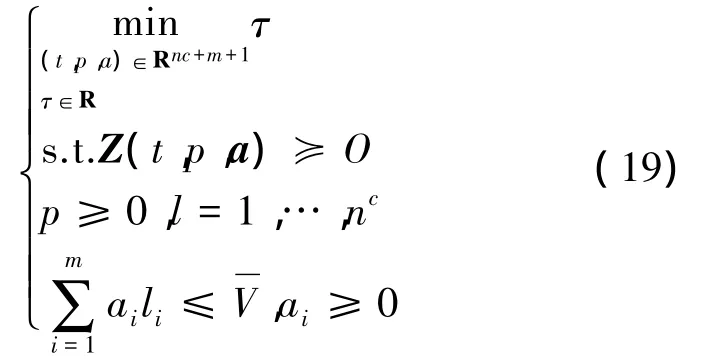
半定規劃算法有成熟的商業計算軟件包，可直接方便快捷調用，避免如牛頓法那樣推導雅可比矩陣和海森堡矩陣。

3 數值仿真

3.1 三桿系穩健性優化

考慮如圖1所示的三桿件架體。其形式為對稱結構，桿件個數和自由度分別為m=3，n=2。為了結果分析方便，這里將單位歸一化處理。桿件3的長度l3=15且垂直于水平方向，θ=45°。桿件所受力狀態如圖1所示，名義載荷大小為100。考慮應力約束式(3)=3.0(i=1，2，3)。設定結構初始變量為a0=(20，20，20)，以a=a0時結構體積為基準，則結構體積約束為≤1 148.53。

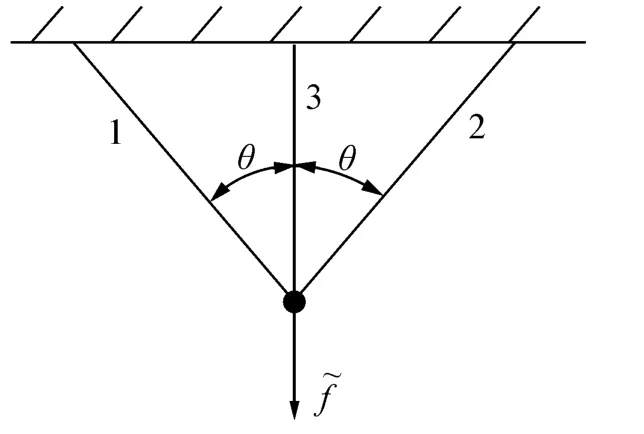
圖1 三桿架體Fig.1 3-bar structure

已知初始變量值a0，對式(18)進行求解，得到(a0，σc)=0.822。通過半定規劃模型式(19)，對架結構進行優化設計，得到優化迭代過程如表1。

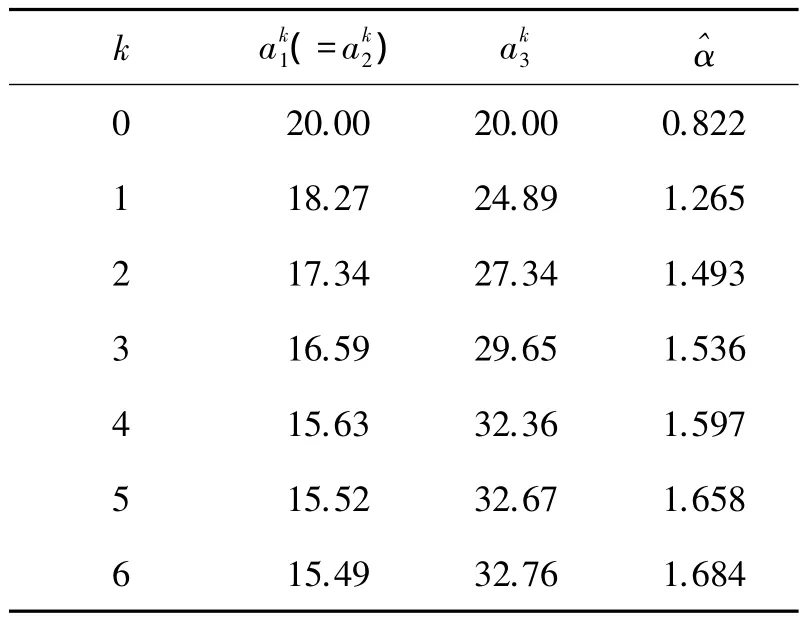
表1 優化迭代過程Table 1 Iteration history of the optimization

對結構初始狀態a0進行分析。隨機產生一組力f，使其落在穩健函數(a0，σc)限定的不確定載荷集之中。則結構中桿件應力σi(i=1，2，3)分布狀態如圖2所示。

經過觀察可以發現，桿件3在應力σ3=3.0附近有分布，而桿件1(或桿件2)應力值始終沒有發揮最大功效。

剛架經過優化后，最優解為a=a*，經過計算和分析，得到結構桿件應力σi(i=1，2，3)分布狀態如圖3所示。其中，應力約束σi≤σc(i=1，2，3)在3個桿件中均產生作用，優化后改善了結構性能，最大程度發揮了剛架體結構的潛力。

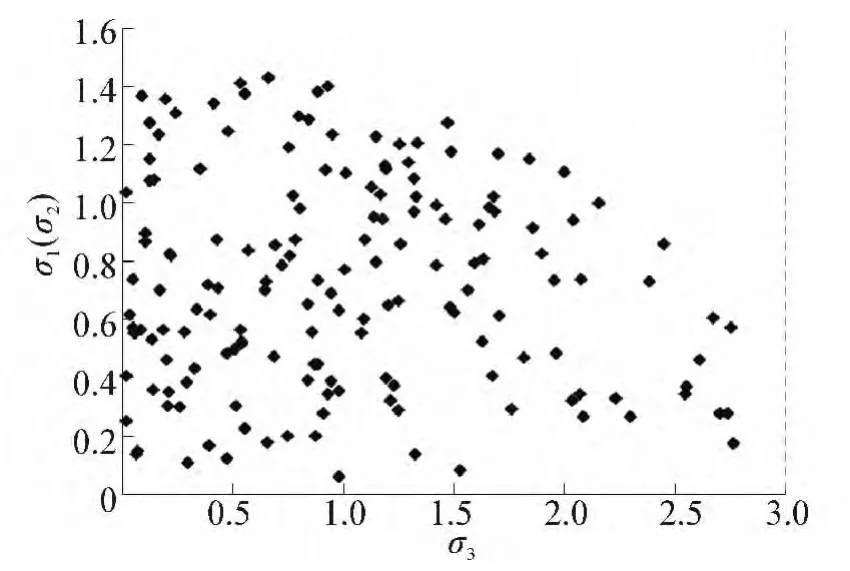
圖2 當a=a0時桿件應力分布Fig.2 Stress states of the 3-barstructure with a=a0

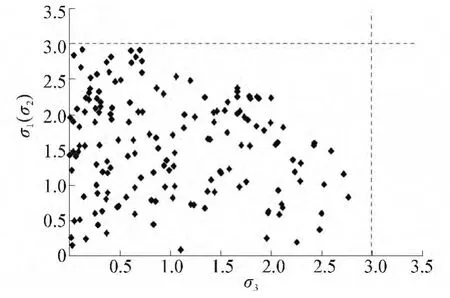
圖3 當a=a*時桿件應力分布Fig.3 Stress states of the 3-barstructure with a=a*

3.2 多桿系剛架體結構

如圖4所示多桿架體結構，桿件個數和自由度分別為m=100，n=90。桿件在x軸和z軸方向的長度均為100，在y軸方向有桿長100和30(即中部連接處短桿)2種規格，其余為連接斜桿。結構底座完全約束。載荷作用于如圖4所示位置，垂直方向載荷名義值為=(0，10，0);水平方向名義值=(2，0，0)。

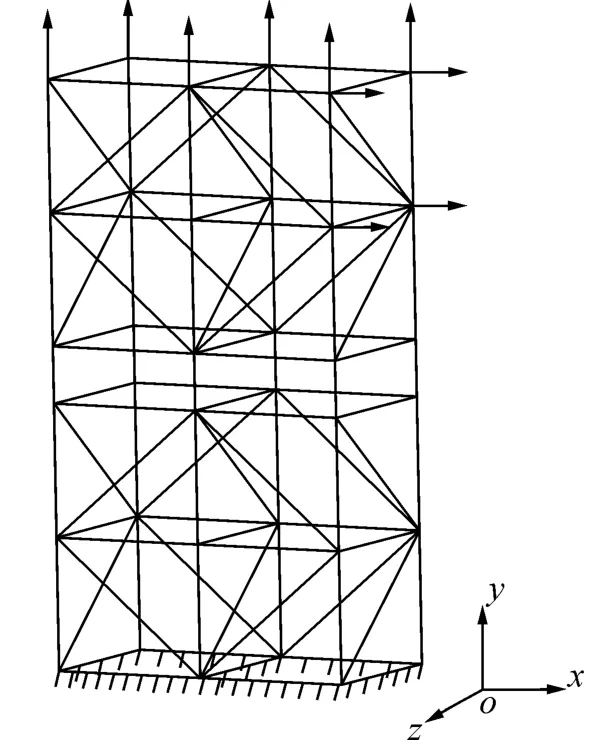
圖4 多桿架結構Fig.4 Complex frame structure

圖5 架體優化設計Fig.5 Optimal design of the frame structure

為了驗證優化結果，觀察后標記如圖6所示，對部分桿件進行分析。當結構中a=a0和a=a*時，產生一組隨機攝動載荷分別滿足應力約束式(3)要求。

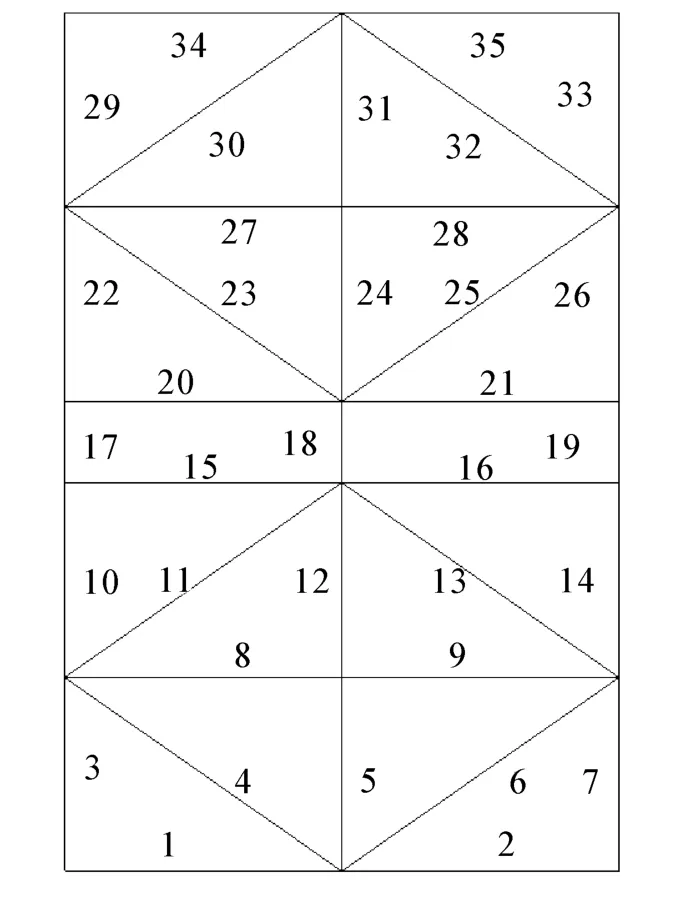
圖6 架體平面結構Fig.6 2-D structure of the frame structure

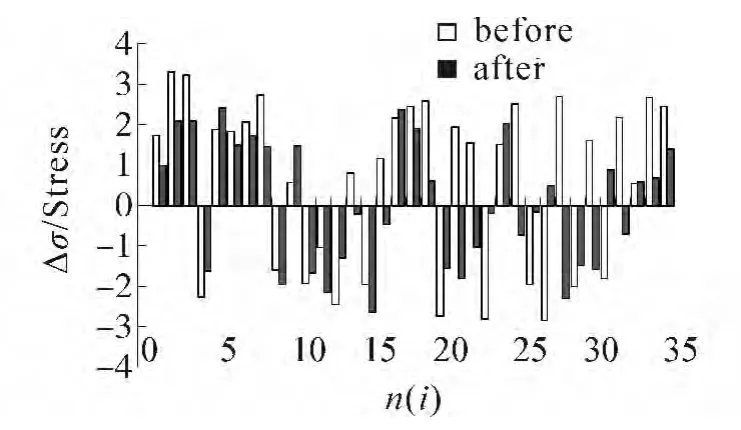
圖7 隨機攝動載荷下最大應力Fig.7 Fluctuation stress under random loading

圖7表示優化前后對比，即對應a=a0、a*時，圖6中標記對應桿桿件最大應力變化范圍。其中淺色為設計變量初始取值，深色為優化后取值。通過觀察發現，優化后結構在隨機攝動載荷下，最大應力變化幅值總體上小于優化前，結構保持較大的安全富裕度，能更好抵抗不確定載荷的影響。

4 結束語

本文基于穩健性函數構建了剛架體結構穩健性優化算法。該方法充分考慮了載荷的不確定因素，利用I-G理論處理不確定載荷，構造應力約束下的穩健性函數最大值優化模型，利用半定規劃松弛技術重新將優化問題轉換成半定規劃問題，降低工程設計人員求解的難度，提高求解效率。通過數值仿真可以發現在優化過程中約束條件發揮作用，在同等體積(質量)條件下，雖結構局部一些桿件應力有所增加，但總體應力狀態得到改善，提高了結構抗擾動載荷的能力。

［1］TAGUCHI G，CHOWDHURY S，TAGUCHI S.Robust engineering［M］.New York:McGraw-Hill，2000:327-533.

［2］張瑞軍，邱繼偉，賈慶軒，等.基于靈敏度附加項的多目標可靠性穩健優化設計［J］.應用基礎與工程科學學報，2013，21(4):777-785.ZHANG Ruijun，QIU Jiwei，JIA Qingxuan，et al.Multi-objective reliability-based robust optimization design based on the sensitivity additional items［J］.Journal of Basic Science and Engineering，2013，21(4):777-785.

［3］丁力平，馮毅雄，譚建榮，等.基于性能穩健指數的產品族穩健優化設計［J］.計算機集成制造系統，2010，16(6):1121-1130.DING Liping，FENG Yixiong，TAN Jianrong，et al.Robust optimization design of product family based on performance robustness index［J］.Computer Integrated Manufacturing Systems，2010，16(6):1121-1130.

［4］高一聰，馮毅雄，譚建榮，等.基于MSRE的機械產品質量特性穩健優化設計方法［J］.計算機集成制造系統，2010，16(5):897-904.GAO Yicong，FENG Yixiong，TAN Jianrong，et al.Product quality characteristics robust optimization design based on minimum sensitivity region estimation［J］.Computer Integrated Manufacturing Systems，2010，16(5):897-904.

［5］李小剛，程錦，劉振宇，等.基于雙層更新Kriging模型的機械結構動態特性穩健優化設計［J］.機械工程學報，2014，50(3):65-173.LI Xiaogang，CHENG Jin，LIU Zhenyu，et al.Robust optimization for dynamic characteristics of mechanical structures based on double renewal kriging model［J］.Journal of Mechanical Engineering，2014，50(3):165-173.

［6］于利磊，唐文勇，張圣坤，等.一種工程結構的魯棒優化設計方法［J］.上海交通大學學報，2003，37(8):1189-1192.YU Lilei，TANG Wenyong，ZHANG Shengkun，et al.Robust optimization design method for engineering structures［J］.Journal of Shanghai Jiaotong University，2003，37(8):1189-1192.

［7］宋述芳，呂震宙.基于高階矩的穩健優化設計研究［J］.力學學報，2012，44(4):735-744.SONG Shufang，LYU Zhenzhou.The robust optimization design based on moment estimation method［J］.Chinese Journal of Theoretical and Applied Mechanics，2012，44(4):735-744.

［8］BEN H Y，ELISHAKOFF I.Convex models of uncertainty in applied mechanics［M］.Amsterdam:Elsevier，1990:175-230.

［9］BEN-HAIM Y.Robust reliability of structures［J］.Advances in Applied Mechanics，1997，33:1-41.

［10］張成，吳慧，高博青，等.非概率不確定性結構的魯棒性分析［J］.計算力學學報，2013，30(1):51-56.ZHANG Cheng，WU Hui，GAO Boqing，et al.Analysis of structural robustness with non-probabilistic uncertainties［J］.Chinese Journal of Computational Mechanics，2013，30(1):51-56.

［11］王曉軍，王磊，賈曉，等.基于非概率凸模型可靠性的結構優化設計［J］.北京航空航天大學學報，2012，38(5):630-635.WANG Xiaojun，WANG Lei，JIA Xiao，et al.Structural optimization design based on non-probabilistic convex modeling reliability［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(5)630-635.

［12］劉曉，徐格寧，楊萍.區間干涉模型下的非概率可靠性應用研究［J］.中國礦業大學學報，2012，41(4):675-680.LIU Xiao，XU Gening，YANG Ping.Application of nonprobabilistic reliability based on interval interference model［J］.Journal of China University of Minging ＆ Technology，2012，41(4):675-680.

［13］石海軍，錢林方，徐亞棟，等.具有參數區間不確定的機械臂結構優化［J］.南京理工大學學報，2014，38(1):100-105.SHI Haijun，QIAN Linfang，XU Yadong，et al.Structural optimization for manipulator with interval uncertainties［J］.Journal of Nanjing University of Science and Technology，2014，38(1):100-105.

［14］WOLKOWICZ H，SAIGAL R，VANDENBERGHE L.Handbook of semidefinite programming:theory，algorithms，and applications［M］.(s.l.):Kluwer Academic Publishers，2000:137-201.

［15］YAKOV B H.Set-models of information-gap uncertainty:axioms and an inference scheme［J］.Journal of the Franklin Institute，1999，336:1093-1117.

［16］YAKOV B H.Uncertainty，probability and information-gaps［J］.Reliability Engineering and System Safety，2004，85:249-266.

［17］蘇永華，李翔.基于Info-Gap理論的地下結構穩健性分析方法［J］.巖土工程學報，2011，33(2):227-233.SU Yonghua，LI Xiang.Robust reliability analysis for underground structures based on Info-Gap theory［J］.Chinese Journal of Geotechnical Engineering，2011，33(2):227-233.

［18］曹文貴，李媛，翟友成.基于Info-Gap理論的基樁下伏巖溶頂板穩定性的主動分析方法［J］.巖石力學與工程學報，2013，32(2):393-400.CAO Wengui，LI Yuan，ZHAI Youcheng.Active analysis method for stability of karst roof under foundation pile based on info-gap theory［J］.Chinese Journal of Rock Mechanics and Engineering，2013，32(2):393-400.