基于CFD的水潤滑靜壓推力軸承承載能力分析

王艷真，蔣　丹，尹忠慰，高庚員，張秀麗

(上海交通大學 機械與動力工程學院，上海 200240)

基于CFD的水潤滑靜壓推力軸承承載能力分析

王艷真，蔣丹，尹忠慰，高庚員，張秀麗

(上海交通大學 機械與動力工程學院，上海 200240)

基于計算流體動力學(CFD)理論，針對某水潤滑靜壓推力軸承建立了不同的水膜模型，分析水膜厚度與軸承承載能力的關系，以及水腔厚度、進水孔直徑、軸承轉速對軸承承載能力的影響.結果表明：隨水膜厚度的增加，靜壓推力軸承承載力顯著減小；隨水腔厚度或進水孔直徑的增加，軸承承載力先增大后基本不變；水腔厚度越大，使承載能力最大的進水孔直徑越小；隨轉速增大，軸承端泄增強，且承載能力明顯下降.

水潤滑；靜壓推力軸承；承載能力；影響參數

目前，軸承的主要潤滑介質仍然為油，近年來對油潤滑的研究已日益成熟，但油潤滑軸承在有些特定工況(如核泵)中不適用，并且其結構復雜，存在一系列嚴重問題，如潤滑油泄漏、環境污染等.水潤滑推力軸承以水為潤滑介質，因其環境友好性及可持續性等優點，水潤滑軸承的應用越來越廣泛[1]，常用于電廠、水輪機、水泵以及螺旋槳等場合.

國外對水潤滑軸承的研究和應用較早，而我國對于水潤滑軸承的研究始于20世紀80年代末，且近年來才逐漸重視對水潤滑軸承的研究.文獻[2]研究了靜壓推力軸承的油腔位置、尺寸對其性能和承載力的影響.文獻[3]給出了靜壓推力軸承的設計參考，并研究了影響軸承動特性的因素.文獻[4]研究了不同腔型的靜壓推力軸承的潤滑特性.文獻[5]研究了油墊深度對動壓效應的影響.文獻[6]基于計算流體動力學(CFD)理論，指出了水潤滑動壓推力軸承承載力的影響因素，并對各因素進行了分析.文獻[1]基于CFD理論建立了不同水潤滑斜面推力軸承的水膜模型，分析了斜面推力軸承承載能力的影響因素，從而為水潤滑斜面推力軸承的設計提供了理論依據.文獻[7]研究了水潤滑石墨推力軸承的摩擦學性能，提出了提高軸承摩擦學性能的方法，設計出適合于主泵機組運行工況的水潤滑推力軸承結構形式，分析潤滑水膜的形成條件.文獻[8]以潛水泵的水潤滑推力軸承為研究對象，開展了推力軸承流體動壓潤滑和彈流潤滑、熱-結構耦合特性以及試驗驗證等方面的研究.文獻[9]運用Matlab軟件編程計算求解了層流和紊流兩種工況下水潤滑推力軸承的水膜厚度分布和壓力分布，并分析計算了推力軸承的運行工況參數和軸承幾何參數對其主要潤滑性能的影響規律，其結論為推力軸承的設計提供了理論依據.以上文獻僅對油潤滑靜壓推力軸承或水潤滑動壓推力軸承進行了研究，探究了影響承載力的因素及軸承的潤滑特性，對水潤滑靜壓推力軸承的承載能力影響因素的研究較少，因此有必要做進一步探索.

本文針對水潤滑靜壓推力軸承，采用CFD軟件Fluent，通過對不同最小水膜厚度、水腔厚度、進水孔直徑及轉速的模型進行仿真計算，得到水膜的承載能力與各因素的關系圖和軸承壓強分布云圖，進一步得到軸承水膜厚度與承載能力的關系以及水腔區域厚度、進水孔直徑大小、軸承轉速與水潤滑靜壓推力軸承承載能力的關系.研究流程如圖1所示.

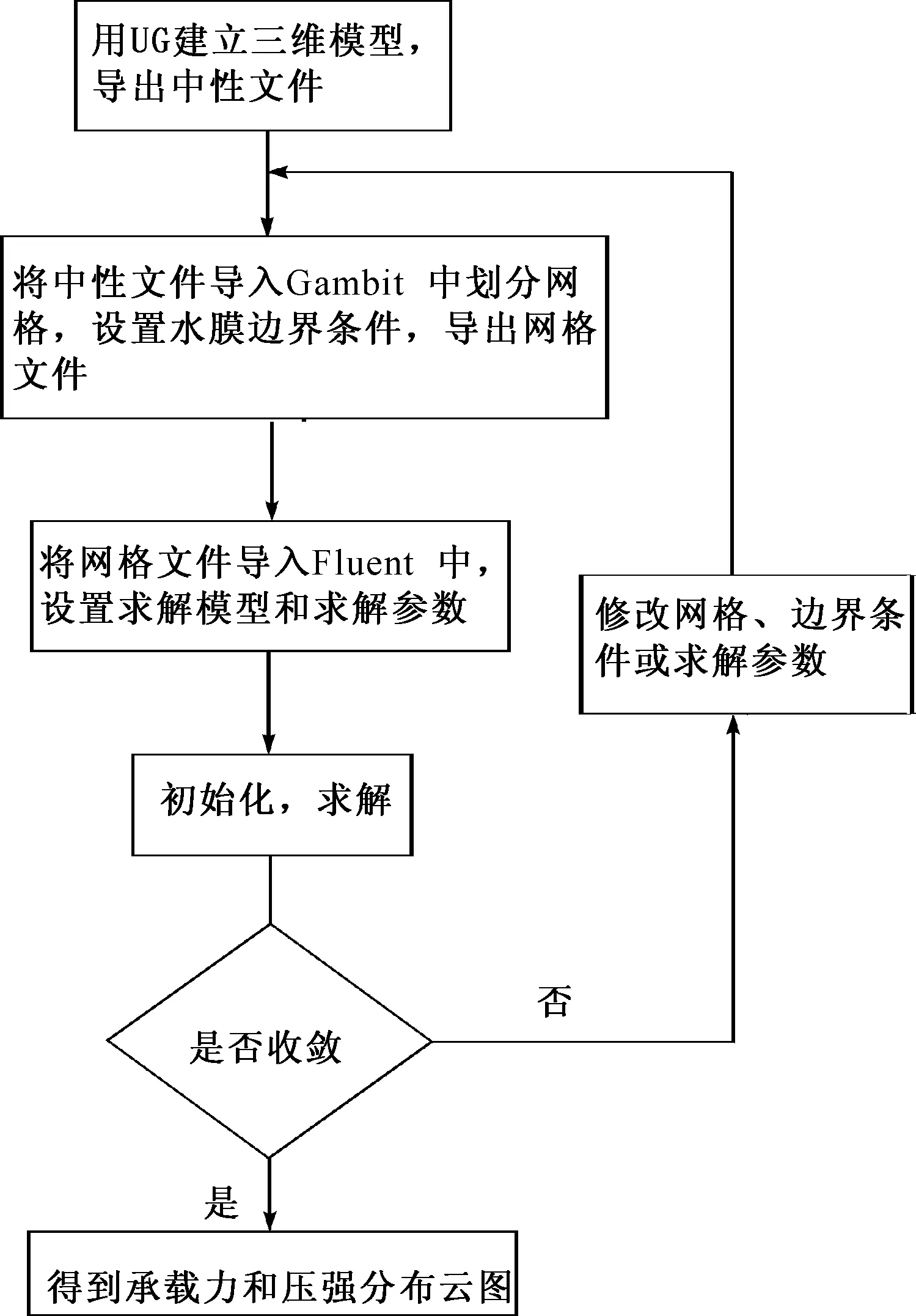
圖1　計算流程Fig.1　Computational procedure

1　水潤滑靜壓推力軸承結構及參數

液體靜壓軸承的基本工作原理是在軸承滑動表面開設液體腔，由外部液壓系統通過進液孔往腔內注入壓力，利用液膜壓力將軸承托起[10].當水潤滑靜壓推力軸承工作時，將具有壓力的水打入水腔中，形成壓力水膜，保證主軸始終懸浮在壓力水膜上，利用靜壓水腔間的壓力差承受軸承本身重量及外載荷.當軸承處于靜壓潤滑狀態時，軸承副兩表面間隙中的水壓力不是由相對運動產生的，而是由軸承外部的水泵產生的.

靜壓軸承系統由承載部分、補償元件和供水液壓系統組成，其中承載部分稱為水腔.本文主要研究多水腔靜壓推力軸承，其系統簡圖如圖2所示.

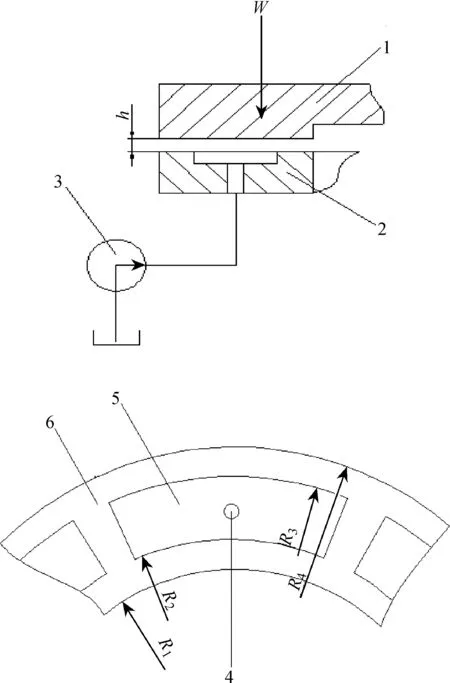
1—工作臺；2—導軌；3—水泵； 4—進水孔；5—水腔；6—封水邊；h—水膜厚度； W—外載荷圖2　水潤滑靜壓推力軸承結構Fig.2　Structure of hydrostatic thrust bearing

2　潤滑理論及水膜模型

2.1水膜控制方程

流體流動所滿足的基本守恒定律包括3項，即質量守恒定律、動量守恒定律和能量守恒定律.由于水溫升高較小，故不考慮能量守恒.這些基本守恒定律均需要用控制方程的形式進行數學描述.

2.1.1質量守恒方程

根據質量守恒定律，可寫出質量守恒方程，又稱連續性方程，如式(1)所示.

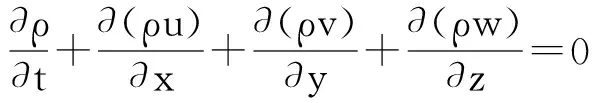
(1)

式中：ρ為流體密度； t為時間；u, v, w 為速度矢量在x, y, z軸方向的分量.

2.1.2動量守恒方程

流體動量守恒方程又稱為Navier-Stokes 方程,如式(2)所示.

式中： p為流體微元體上的壓力；μ為動力黏度.

2.2流態分析

在潤滑理論中，慣性力與黏性力的比值用雷諾數(Re)[11]表示，如式(3)所示.

(3)

式中：μ為流體的動力黏度(Pa·s)；hm為流體膜厚均值(m)；v為流體流速(m/s)；ρ為流體密度(kg/m3).

大量試驗與理論表明，液體從層流向紊流轉變的臨界雷諾數為1 000～1 500[12].本文采用的雷諾數為1 500.

對于本文中的水潤滑靜壓推力軸承，其雷諾數表達式如下：

式中：ρ =103kg/m3；Ro為推力軸承的中徑，Ro=192.5 mm；μ=10-3Pa·s.經計算可得：n·hmax= 0.074448 m·r/min，若軸承轉速n=3500 r/min，則計算得到從層流轉變為紊流的最大水膜厚hmax=21.17 μm.本文所考慮的水流動狀態均在此范圍內，即滿足n·hmax=0.074448 m·r/min，故采用層流進行仿真計算.

2.3水膜模型的建立

本文采用周期邊界條件，將瓦塊兩側水膜設置為旋轉周期邊界，一個瓦塊的潤滑模型通過對稱即可得到總體的潤滑模型.所選取的推力環轉速為0～3500 r/min.邊界條件設置如下：進水孔壓強為泵壓，出口壓強設置為大氣壓.水膜的計算模型如圖3所示.

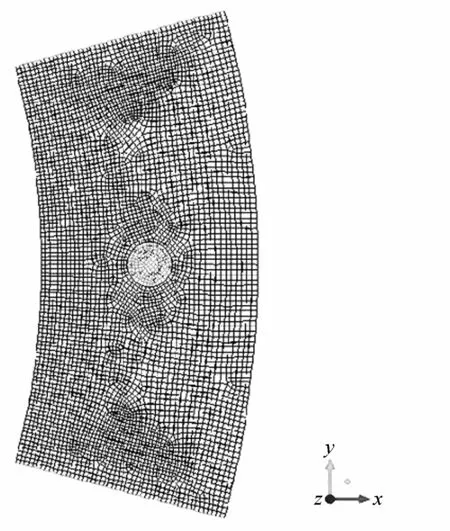
圖3　計算模型Fig.3　Calculation model

3　結果及分析

3.1水膜厚度對水潤滑靜壓推力軸承承載能力的影響

為得到水膜厚度與軸承承載能力之間的關系，當轉速為750 r/min，水腔厚度為3.2 mm，進水孔直徑和長度分別為16和4 mm，入口壓強為0.5 MPa時，分別計算了不同水膜厚度下(0.03～0.50 mm)的軸承承載能力，其結果如圖4所示，其中，承載能力以軸瓦工作面上單位面積所承受的載荷(即比壓)來表示.由圖4可知，隨水膜厚度的增加，承載能力顯著下降；水膜厚度為0.07與0.30 mm是承載能力變化的轉折點.由于水潤滑靜壓推力軸承隨膜厚的增加承載能力下降顯著，故要得到大的承載能力，對軸承表面的加工精度要求更高，最適宜的水膜厚度為0.09 mm左右.

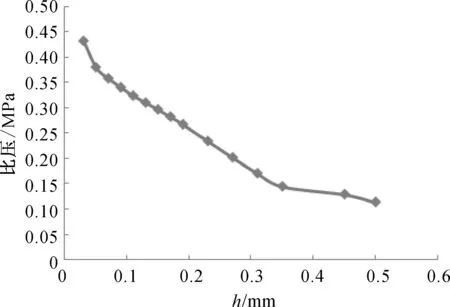
圖4　水膜厚度對水潤滑靜壓推力軸承承載能力的影響Fig.4　The influence of water film thickness on the load capacity of the water lubricated hydrostatic thrust bearing

圖5給出了水膜厚度h分別為0.07， 0.09， 0.11， 0.13 mm時的水膜壓強分布云圖.由圖5可知，當h為0.07，0.09 mm時，由于軸承旋轉時形成動壓，最大壓強分別為5.15×105， 5.03×105Pa，均大于入口壓強5.0×105Pa；當h為0.11， 0.13 mm時，水腔區的最大壓強均等于入口壓強.

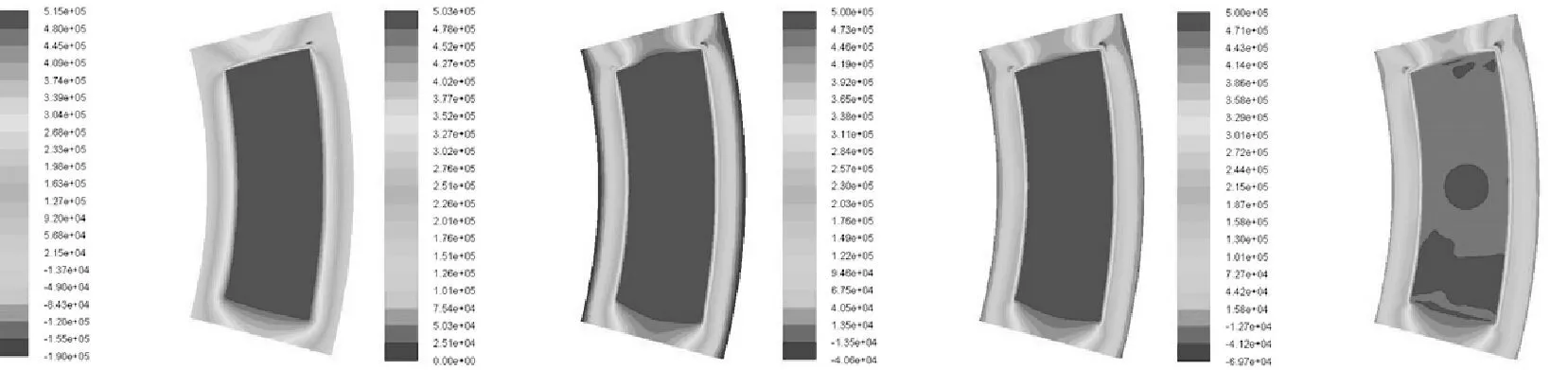
h=0.07 mm　h=0.09 mm　h =0.11 mm　h=0.13 mm圖5　水膜厚度對壓強分布的影響Fig.5　 The effect on water film pressure distribution for different water film thickness

3.2水腔厚度對水潤滑靜壓推力軸承承載能力的影響

當軸承轉速為750 r/min，水膜厚度為0.1 mm，進水孔深度為4 mm，進水孔直徑為16 mm時，水腔厚度與承載能力之間的關系如圖6所示.由圖6可知，軸承承載能力隨水腔厚度的增大而增大.當水腔厚度小于1.6 mm時，隨水腔厚度的增加，軸承承載能力的變化率較大；當水腔厚度大于1.6 mm時，隨水腔厚度的增加，軸承承載能力的變化率很小.

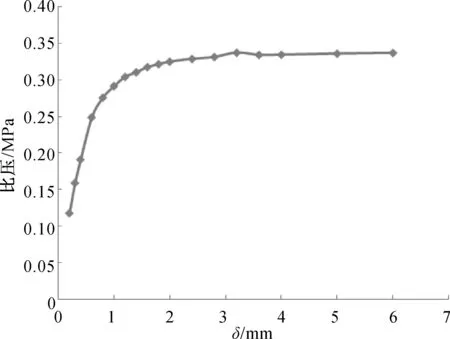
圖6　水腔厚度對水潤滑靜壓推力軸承承載能力的影響Fig.6　 The influence of water cavity thickness on the load capacity of the water lubricated hydrostatic thrust bearing

圖7給出了不同水腔厚度δ的水膜壓強分布.由圖7可知，隨著水腔厚度的增大，水腔區的壓力逐漸增大，直至達到入口壓力0.5 MPa時軸承承載能力達到最大值.

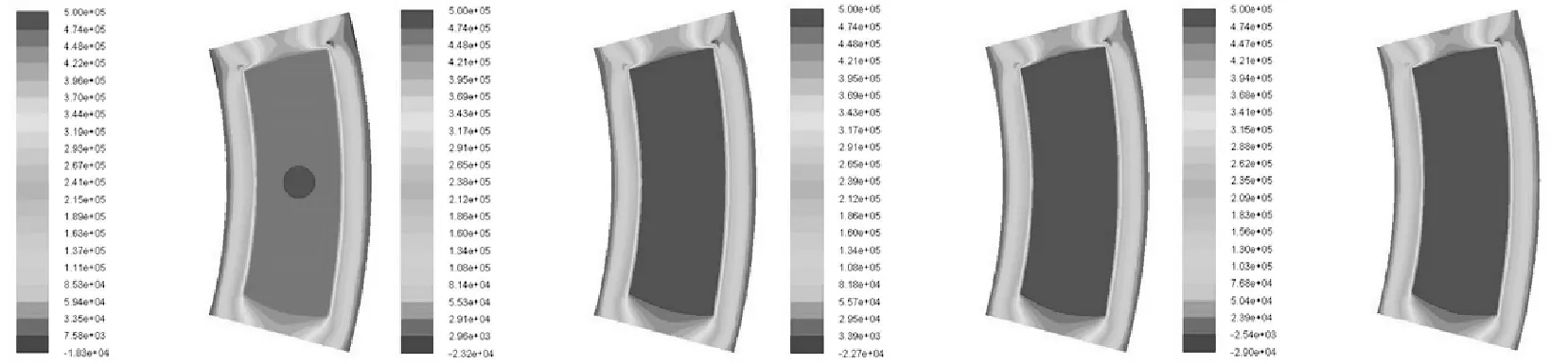
δ=1.6 mm　δ=2.4 mm　δ=3.2 mm　δ=4.0 mm圖7　水腔厚度的水膜壓強分布的影響Fig.7　 The effect on water film pressure distribution for different water cavity thickness

3.3進水孔直徑對水潤滑靜壓推力軸承承載能力的影響

當軸承轉速為750 r/min，水膜厚度為0.1 mm，入口壓力為0.5 MPa，水腔厚度分別取0.8， 1.6， 3.2 mm時，不同進水孔直徑(6～40 mm)與水潤滑靜壓推力軸承承載能力關系如圖8所示.由圖8可知，進水孔直徑是顯著影響水潤滑靜壓推力軸承承載能力的重要因素.隨進水孔直徑和水腔厚度的增大，軸承承載能力增強；水腔越厚，使軸承承載力最大的進水孔直徑越小；同一水腔厚度下，隨進水孔直徑的增大，承載能力的變化率逐漸減小；當進水孔直徑接近40 mm時，不同水腔厚度的軸承均達到最大承載能力，且此時承載能力接近同一值；當水腔厚度為3.2 mm時，使軸承承載力最大的進水孔直徑為16 mm.

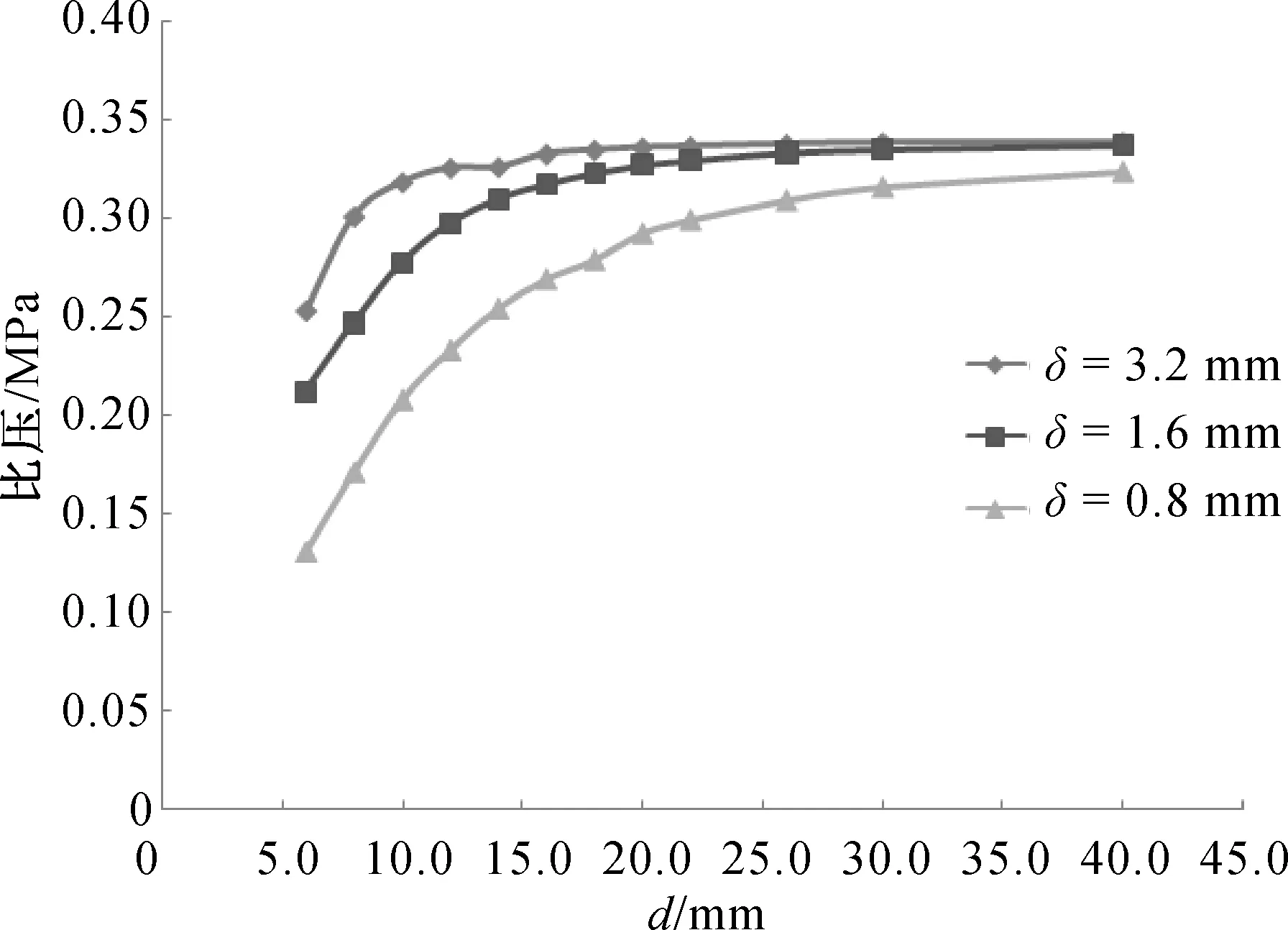
圖8　進水孔直徑對水潤滑靜壓推力軸承承載能力的影響Fig.8　 The influence of inlet opening diameter on the load capacity of the water lubricated hydrostatic thrust bearing

當水腔厚度為3.2 mm時，不同進水孔直徑d的水膜壓強分布如圖9所示.由圖9可看出，隨進水孔直徑的增加，水腔區的壓強逐漸增大，直至等于入口壓強0.5 MPa，與此同時軸承的承載能力也逐漸增加.

3.4軸承轉速對水潤滑靜壓推力軸承承載能力的影響

為研究軸承轉速對水潤滑靜壓推力軸承承載能力的影響，取水膜厚度為0.1 mm，水腔厚度為3.0 mm，進水孔直徑為16 mm，入口壓強為0.5 MPa情況下，分別計算了不同轉速下軸承的承載能力,結果如圖10所示.由圖10可知，隨轉速的增加，由于軸承的端泄增大，靜壓軸承承載能力下降，轉速是影響靜壓軸承水膜承載能力的重要因素.當軸承轉速為200 r/min時，其比壓為0.336 MPa；當轉速為2000 r/min時，其比壓為0.319 MPa.從圖10中還可看出，當轉速小于600 r/min時，隨轉速的增大，軸承承載能力下降的趨勢較為緩慢；當轉速大于600 r/min時，隨轉速的增大，水潤滑推力軸承的承載能力基本按恒定斜率下降.

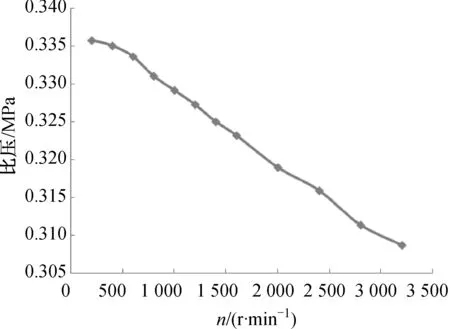
圖10　轉速對水潤滑靜壓推力軸承承載能力的影響Fig.10　 The influence of rotational speed on the load capacity of the water lubricated hydrostatic thrust bearing

圖11為不同軸承轉速的水膜壓強分布圖(僅給出了轉速為200～1600 r/min時的壓力分布圖).從圖11可看出，靜壓推力軸承的壓強從水腔到邊緣逐漸減小；轉速為200 r/min左右時，由于動壓效應水腔區的實際壓強大于入口壓強.

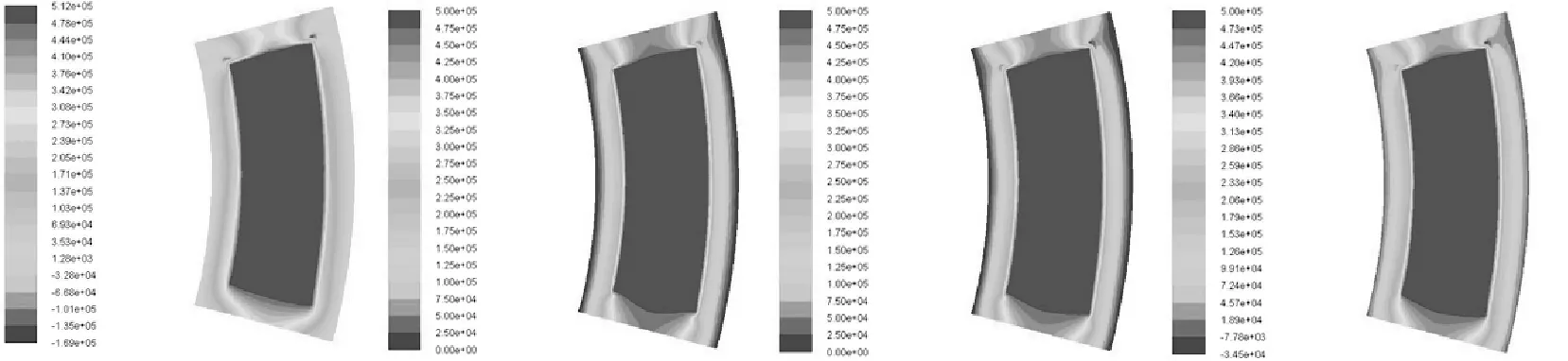
n=200 r/mimn=400 r/mimn=600 r/mimn=800 r/mim

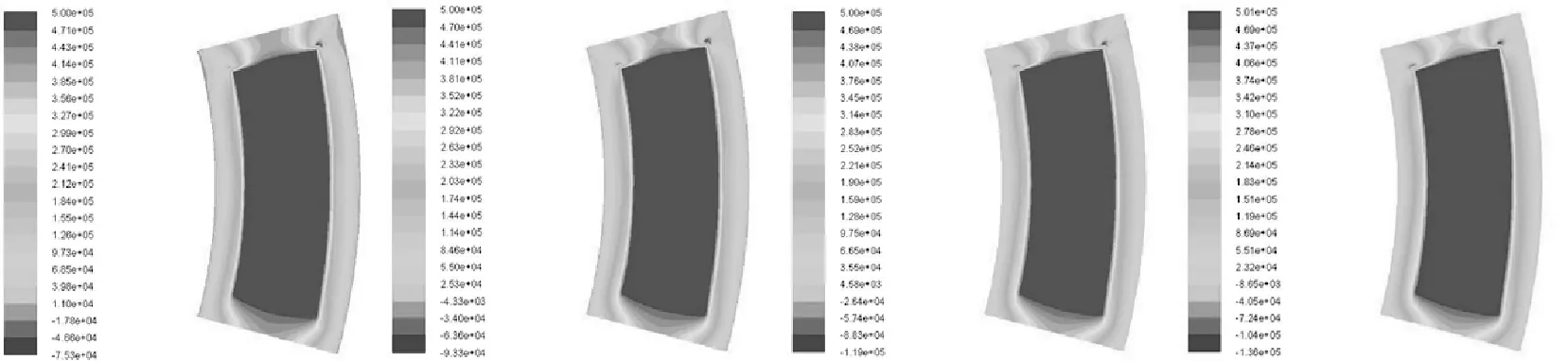
n=1 000 r/mimn=1 200 r/mimn=1 400 r/mimn=1 600 r/mim圖11　轉速對水膜壓強分布的影響Fig.11　 The effect on water film pressure distribution for different rotational speed

4　結　語

(1) 隨水膜厚度的增加，水潤滑靜壓推力軸承的承載能力顯著減小，故要提高該軸承的承載能力，設計的軸承間隙將大幅減小，這對軸承的加工精度有更高要求；

(2) 水腔厚度和進水孔直徑是影響水潤滑靜壓推力軸承承載能力的重要因素.隨水腔厚度或進水孔直徑的增加，軸承承載能力先增大后基本不變；

(3) 水腔越厚，使承載能力最大的進水孔直徑越小；

(4) 隨軸承轉速的增加，軸承的端泄增大，靜壓軸承承載能力顯著下降；當轉速較小時，隨轉速的增大，承載能力下降的趨勢較為緩慢；當轉速較大時，隨轉速的增大，承載能力的下降基本和轉速成線性關系.

[1] 張秀麗, 蔣丹, 尹忠慰, 等. 基于 CFD 的水潤滑斜面推力軸承承載能力分析[J]. 東華大學學報: 自然科學版, 2013, 39(4): 411-416.

[2] OSMAN T A, DORID M, SAFAR Z S, et al. Experimental assessment of hydrostatic thrust bearing performance[J]. Tribology International, 1996, 29(3): 233-239.

[3] OSMAN T A, SAFAR Z S, MOKHTAR M O A. Design of annular recess hydrostatic thrust bearing under dynamic loading[J]. Tribology International, 1991, 24(3): 137-141.

[4] SHARMA S C, JAIN S C, BHARUKA D K. Influence of recess shape on the performance of a capillary compensated circular thrust pad hydrostatic bearing[J]. Tribology International, 2002, 35(6): 347-356.

[5] SHAO J, ZHOU L, LI H, et al. Influence of the oil cavity depth on dynamic pressure effect of hydrostatic thrust bearing[C]//Intelligent Human-Machine Systems and Cybernetics, 2009.

[6] 張霞,周勇,王新榮,等.水潤滑推力軸承承載力影響因素及提高方法研究[J].機械制造,2011,49(4):16-19.

[7] 楊麗華. 水潤滑石墨推力軸承摩擦學性能研究[D]. 佳木斯：佳木斯大學機械工程學院, 2013.

[8] 何春勇, 劉正林, 吳鑄新. 潛水泵水潤滑推力軸承潤滑性能數值分析[J]. 潤滑與密封, 2010 (8): 59-62.

[9] 劉奇. 大型水潤滑推力軸承承載性能及推力瓦型面優化研究[D].太原：中北大學機械與動力工程學院, 2013.

[10] 李洪，曲中謙. 實用軸承手冊[M]. 沈陽：遼寧科學技術出版社, 2001.

[11] 鄧禮平.推力軸承層流向紊流轉變區域的理論分析[J].潤滑與密封, 1997,22(4):5-9.

[12] 溫詩鑄, 黃平. 摩擦學原理[M]. 北京：清華大學出版社，1990：20.

Load Capacity Analysis of Water Lubricated Hydrostatic Thrust Bearing Based on CFD

WANGYan-zhen,JIANGDan,YINZhong-wei,GAOGeng-yuan,ZHANGXiu-li

(School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China)

Based on the theory of computational fluid dynamics (CFD), different water hydrostatic thrust bearing models were established . The influence of the thickness of water film, water cavity thickness, inlet opening diameter, and rotational speed on the load capacity of the hydrostatic thrust bearing were analysed. The results indicate that load capacity significantly decreases with the increase of film thickness; with the increase of the water cavity thickness or inlet opening diameter, load capacity increases ,then basically remains unchanged; the water cavity is thicker, the inlet opening diameter is smaller for the maximum load capacity; load capacity decreases as the discharge increases with the increase of rotational speed.

water lubrication; hydrostatic thrust bearing; load capacity; influence parameters

1671-0444(2015)04-0428-05

2014-10-27

國家自然科學基金資助項目( 50875169)

王艷真(1991—)，女，河北邢臺人，碩士研究生，研究方向水潤滑軸承. E-mail: merinawang@163.com

蔣丹(聯系人)，女，教授，E-mail: jiangdan@sjtu.edu.cn

TH 133.37

A