基于Epiphany 計(jì)算并行矩陣乘法的研究

曾弘揚(yáng)

（北京工業(yè)大學(xué) 軟件學(xué)院， 北京 100124）

對(duì)于工程科學(xué)中的許多計(jì)算問(wèn)題中，數(shù)值計(jì)算問(wèn)題都是最基本的內(nèi)容。 矩陣乘法作為基本的線性代數(shù)運(yùn)算，被廣泛地應(yīng)用于工程學(xué)領(lǐng)域[1]。 矩陣乘積在實(shí)際應(yīng)用中是經(jīng)常要用到的，例如，在解決有限元素的方法中，模型元素之間的關(guān)系被表示為狀態(tài)矩陣元素。 對(duì)狀態(tài)的改變，被表示成輸入一個(gè)矩陣或向量，通過(guò)進(jìn)行矩陣乘法來(lái)計(jì)算出新的狀態(tài)。 所以如何高效的計(jì)算矩陣乘法是十分重要的。

1 矩陣乘法的串行實(shí)現(xiàn)

矩陣相乘串行實(shí)現(xiàn)的i－j－k 形式， 其中最內(nèi)層運(yùn)算是點(diǎn)積，數(shù)據(jù)用到A 的行和B 的列。

for（i=0；i＜M；i++）

for（j=0；j＜N；j++）

for（k=0；k＜P；k++）

C[i][j]+=A[i][k]*B[K][j]；

矩陣相乘的前提條件，前一個(gè)矩陣列數(shù)，須與后一個(gè)矩陣行數(shù)相等。 矩陣A 為M 行P 列，矩陣B 為P 行N 列，則矩陣乘法，繼承前一個(gè)矩陣的行數(shù)M，和后一個(gè)矩陣的列數(shù)N，相乘矩陣中每一項(xiàng)，都要經(jīng)過(guò)P 次加和乘。 算法分析：該算法需要進(jìn)行n3個(gè)乘法運(yùn)算和n3個(gè)加法運(yùn)算， 順序代碼的時(shí)間復(fù)雜度為O（n3）。

2 串行計(jì)算大矩陣乘法的問(wèn)題

2.1 串行計(jì)算不適應(yīng)于大矩陣乘法

許多先進(jìn)的計(jì)算機(jī)都配有高效的用于解矩陣乘法的的串行程序庫(kù)，比如常用的SGEMM（單精度普通矩陣乘法）函數(shù)就是用于實(shí)現(xiàn)矩陣乘法運(yùn)算一個(gè)常規(guī)形式的標(biāo)準(zhǔn)API，但它不適用于很大的矩陣。 因此，為了在并行計(jì)算環(huán)境下實(shí)現(xiàn)矩陣乘積，研究并行矩陣乘法是非常必要的[2]。

2.2 并行計(jì)算時(shí)數(shù)據(jù)在多核間的傳輸速率慢

在多核處理器上，當(dāng)操作的矩陣足夠大時(shí)，數(shù)據(jù)就必須從外部?jī)?nèi)存中取出，例如系統(tǒng)的DRAM。 而Epiphany 芯片的外部?jī)?nèi)存DRAM，通過(guò)eMesh 網(wǎng)絡(luò)在STARTIX FPGA 上來(lái)連接。 這個(gè)擴(kuò)展的eMesh 時(shí)鐘頻率是50 MHz，相較于芯片的時(shí)鐘來(lái)說(shuō)是很慢。 因此，數(shù)據(jù)在DRAM 的傳輸非常緩慢。 通過(guò)eMesh 連接的Epiphany 能夠在每個(gè)時(shí)鐘周期讀寫一個(gè)字節(jié)的數(shù)據(jù)。 在一個(gè)負(fù)載均衡的系統(tǒng)上，400 MHz 的Epiphany E16G3 芯片， 從芯片到DRAM 的理論寫速率是400 MB/s，但實(shí)際測(cè)量到的寫速率是82 MB/s[3]。

可見，為了生成優(yōu)化的代碼，應(yīng)盡可能減少對(duì)速度相對(duì)緩慢的DRAM 的訪問(wèn)。因此，在設(shè)計(jì)算法時(shí)，我們必須試圖盡可能多的去重復(fù)利用這些讀取出來(lái)的數(shù)據(jù)。

3 矩陣向量乘法的并行計(jì)算

矩陣與向量相乘是線性方程組迭代求解的核心問(wèn)題，其并行計(jì)算的效率直接影響迭代求解的整體效率。n 階矩陣A，與n 維向量x=[x1x2… xn]T，并行計(jì)算A 與x 的乘積y=[y1y2…yn]T。

并行矩陣向量乘法，對(duì)矩陣采用一維塊狀劃分（帶狀劃分），即把矩陣按整行（或整列）劃分成組，將每組的數(shù)據(jù)指派給一個(gè)處理器存儲(chǔ)。 劃分的這些行列可以是連續(xù)的（連續(xù)帶狀劃分），也可以是等距相間的（循環(huán)帶狀劃分）。 這里，我們對(duì)矩陣A 進(jìn)行按列連續(xù)劃分， 將矩陣A 按行連續(xù)劃分成p塊，則每塊所占行數(shù)為n/p 行（其中n 能被p 整除）。同時(shí)再將每個(gè)行塊按列也相應(yīng)地劃分成p 個(gè)子塊， 則第k 個(gè)行塊Ak又可 進(jìn)一步劃 分為[Ak，0Ak，1… Ak，p－1]。 則Ak，j可以表 示如下：

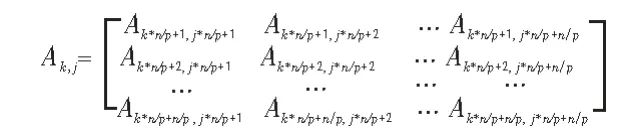
圖1 矩陣的二維網(wǎng)格劃分Fig. 1 The matrix of the two-dimensional grid

圖1 中劃分矩陣A 的下標(biāo)k 是按行連續(xù)劃分的下標(biāo)，下標(biāo)j 是與處理器個(gè)數(shù)相對(duì)應(yīng)的列上劃分， 它們都與處理器個(gè)數(shù)p 相關(guān)，因此范圍都是[0，…，p－1]。

n 階矩陣A 的子塊分成了n/p 階， 同理后面所要乘的向量x，與所得新向量y 的子塊，也都要分成行為n/p 的子塊，因此也都要按 行來(lái)進(jìn)行 劃分成：x=[x0x1…xp－1]T，y=[y0y1… yp－1]T，它們對(duì)應(yīng)成的第k 塊分別是：xk=[xk*n/p+1xk*n/p+2… xk*n/p+n/p]T，yk=[yk*n/p+1yk*n/p+2… yk*n/p+n/p]T。 劃分到處理器上，在處理器k 上進(jìn)行的第k 塊乘積yk的計(jì)算公式為：

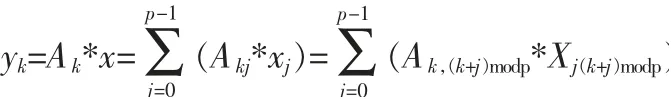
列下標(biāo)j 按[0，1， …，p－1]移動(dòng)時(shí)，下標(biāo)（k+j） mod xk的模依次為[k，k+1，…，k－1]，即先做本地處理器上的Ak，kxk，再做Ak，k+1xk+1，…，就這樣不斷地循環(huán)向下移動(dòng)，直至做到Ak，k+1xk－1完成整個(gè)循環(huán)， 即按順序逐次遍歷完整個(gè)x 向量上的每一個(gè)子塊為止。

矩陣A 的子塊行坐標(biāo)始終為k 不變，即按上式進(jìn)行計(jì)算時(shí)，所用到的矩陣A 中的子塊，就存儲(chǔ)在當(dāng)前運(yùn)行的處理器上。而向量x 的子向量下標(biāo)為（k+j） mod p，會(huì)隨著j 的變化而變化， 即在計(jì)算的過(guò)程中需要用到整個(gè)x 向量上的所有子向量，因此可以通過(guò)在每次計(jì)算完成后，就將處理器中所存儲(chǔ)的x 子向量，循環(huán)向上移動(dòng)到上一列的處理器中。

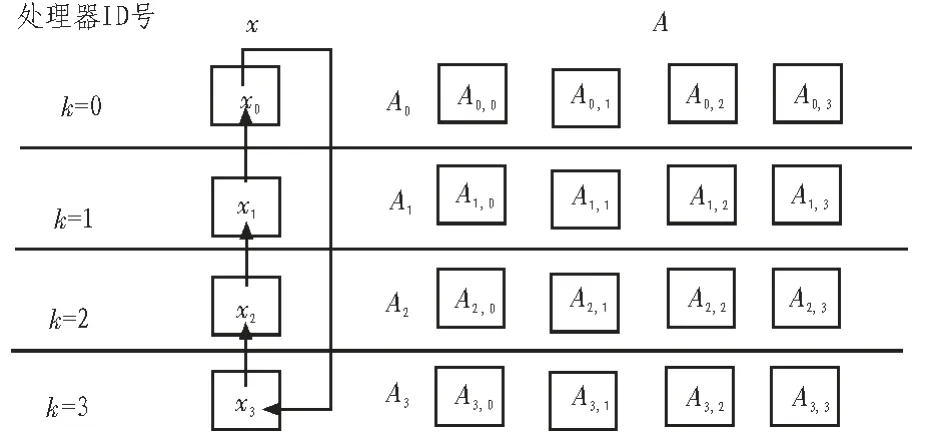
圖2 并行計(jì)算矩陣向量乘積Fig. 2 Parallel computing matrix vector product

如圖2 所示， 將各處理器中所存儲(chǔ)的矩陣A 中的子塊Ak，與處理器中存儲(chǔ)的向量x 的當(dāng)前子塊xk相乘，進(jìn)行p 次，每次x 向量中的子向量都向上循環(huán)移動(dòng)一個(gè)位置， 對(duì)同一處理器中p 次的乘積進(jìn)行累加求和， 即可得出矩陣向量的乘積向量y。

4 矩陣乘法的并行Cannon 算法實(shí)現(xiàn)

根據(jù)矩陣A 與矩陣B 在處理器中的不同存儲(chǔ)方式可得到多種并行計(jì)算矩陣乘積的劃分方法。 比如：行列劃分算法，將矩陣A 按行連續(xù)劃分成p 個(gè)一維塊狀子矩陣（行塊），將矩陣B 按列連續(xù)劃分成p 個(gè)一維塊狀子矩陣（列塊）。 但無(wú)論是按行列、行行、列列，還是按列行來(lái)對(duì)矩陣進(jìn)行劃分，其本質(zhì)都是基于矩陣的一維塊狀劃分。而Cannon 算法是基于矩陣的二維塊狀劃分的。 其特點(diǎn)是矩陣A 中的子塊在指定行中循環(huán)移動(dòng)，矩陣B 中的子塊在指定列中循環(huán)移動(dòng)，對(duì)每個(gè)處理器來(lái)說(shuō)，計(jì)算量都是相同的，具有很好的負(fù)載均衡。 當(dāng)p＞=4 時(shí)，Cannon 算法具有優(yōu)越性[4]。

4.1 二維連續(xù)塊狀劃分

Cannon 算法中并行計(jì)算矩陣的乘法，與并行計(jì)算矩陣向量的乘法原理類似。但不同于矩陣向量的乘法中，只讓一邊的矩陣的各子矩陣循環(huán)移動(dòng)。Cannon 算法是通過(guò)矩陣A 中的各行塊，與矩陣B 中的各列塊同時(shí)進(jìn)行循環(huán)移位，來(lái)完成對(duì)矩陣C 中子塊的計(jì)算。

一個(gè)二維網(wǎng)絡(luò)由p*p 個(gè)處理器組成，將矩陣A、B、C 各劃分成p*p 塊，按二維連續(xù)塊狀進(jìn)行劃分，如上面的矩陣A 圖的形式。 則處理器Pi，j上面的子矩陣Ci，j的計(jì)算公式如下：

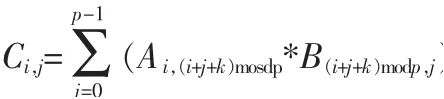
其中，i 是行下標(biāo)，j 是列下標(biāo)，范圍都是[0，p－1]。 而k 是點(diǎn)積次數(shù)，即在m*l*n 中所乘的相同維度的l，因此k 的范圍同其他維度一樣也是[0，p－1]。

k 從0 變化到p－1 時(shí)，（i+j+k） mod p 也從0 取到p－1，k每增加1， 相應(yīng)的行列坐標(biāo)也循環(huán)遞增1。 因此，i，（i+j+k）mod p 是i 行的所有塊，（i+j+k） mod p，j 是j 列的所有塊。 所以，式子中的Ci，j就是A 的i 行上與B 的j 列上對(duì)應(yīng)的所有塊乘積之和。

4.2 對(duì) 準(zhǔn)

相乘的關(guān)鍵是相乘的兩個(gè)元素下標(biāo)要滿足對(duì)準(zhǔn)的要求。

在存儲(chǔ)數(shù)據(jù)時(shí)， 處理器Pi，j上存儲(chǔ)的數(shù)據(jù)應(yīng)當(dāng)是矩陣A的子塊Ai，j，與矩陣B 的子塊Bi，j。 而在計(jì)算開始時(shí)，從初始狀態(tài)k=0 開 始，在處理器Pi，j上處 理 的 是Ai，（i+j）modp* B（i+j）modp，j的乘積。 可見，需要處理的兩個(gè)子塊均不在當(dāng)前的處理器上。 因此，在計(jì)算k=0 狀態(tài)之前，須要先進(jìn)行對(duì)準(zhǔn)操作，將處理器Pi，（i+j）modp上的子塊Ai，（i+j）modp及處理器P（i+j）modp，j上的子塊B（i+j）modp，j都先傳遞到Pi，j上后，才能開始計(jì)算。 即對(duì)p*p 二維網(wǎng)格上的每一個(gè)處理器Pi，j來(lái)說(shuō)，都要進(jìn)行的對(duì)準(zhǔn)操作是，先將其上A的子塊向左循環(huán)移動(dòng)i 個(gè)位置，傳遞給位于i 行（i+j） mod p列上的處理器； 再將其上B 的子塊向上循環(huán)移動(dòng)j 個(gè)位置，傳遞給位于（i+j）mod p 行j 列上的處理器。

對(duì)準(zhǔn)完成后，就可以從k=0 起始，從0 到p-1 按步進(jìn)行計(jì)算了。

4.3 反對(duì)準(zhǔn)

當(dāng)計(jì)算p 次，即第p-1 次計(jì)算結(jié)束后，在Pi，j上參與計(jì)算的子塊實(shí)際是Ai，（i+j+k）modp和B（i+j+k）modp，j。要想將之 前執(zhí)行的 對(duì)準(zhǔn)進(jìn)行還原，需要進(jìn)行反對(duì)準(zhǔn)，使Pi，j上存儲(chǔ)的操作子塊恢復(fù)成Ai，j與Bi，j。 因此，要將多核 上的每一個(gè)處理 器Pi，j上存儲(chǔ) 的A矩陣子塊向右循環(huán)移動(dòng)i 個(gè)位置，B 矩陣子塊向下循環(huán)移動(dòng)j個(gè)位置。

5 基于Epiphany 的矩陣乘法的Cannon 算法

為了實(shí)現(xiàn)一個(gè)任意大小矩陣乘法的高效的多核并行運(yùn)算，需要使用單線程的C 代碼來(lái)構(gòu)建運(yùn)算中的子塊。其中，內(nèi)存的分配被分為兩個(gè)主要部分。 第一部分，是在芯片上每一個(gè)單核上的內(nèi)存。 里面存放的是子塊點(diǎn)積計(jì)算的結(jié)果。 第二部分，是芯片外的DRAM。 在這里，存放的是要操作的A、B、C矩陣。 以及，應(yīng)用于系統(tǒng)層的主從設(shè)備間通信的Mailbox，和用于控制主從設(shè)備交互的結(jié)構(gòu)體。

5.1 程序在核間的存儲(chǔ)

圖3 單核中的內(nèi)存分配Fig. 3 The mononuclear memory allocation

Epiphany 芯片的每個(gè)核都具有32 kb 的SRAM， 將其分配成4 個(gè)8 kb 的bank。每個(gè)核都可并發(fā)訪問(wèn)多個(gè)bank，且不會(huì)帶來(lái)性能損失。 bank 0 用來(lái)存儲(chǔ)程序代碼。 bank 1 用來(lái)存放操作矩陣A 中子塊的兩個(gè)緩存。 同理，bank 2 用來(lái)存放操作矩陣B 中子塊的兩個(gè)緩存。 將bank 3 中的內(nèi)存等分為兩部分。 bank 3 中低位的部分，用于存放矩陣C 中子塊的計(jì)算結(jié)果，因?yàn)橛?jì)算結(jié)束后，也不需寫回計(jì)算后的結(jié)果，因此不需要用兩個(gè)緩存來(lái)存放矩陣C 中的子塊。 將bank 3 中高位的部分， 用于存放對(duì)單核進(jìn)行控制的結(jié)構(gòu)體， 和核間交互的mailbox，以及運(yùn)行bank 0 中代碼時(shí)，程序所需要的棧。內(nèi)存分塊情形如圖3 所示。

5.2 子塊在多核間的傳遞

為了討論方便，先給出一些記號(hào)的約定：

假設(shè)有p 個(gè)處理器，每個(gè)處理器上運(yùn)行一個(gè)進(jìn)程，則Pj表示第j 個(gè)處理器或進(jìn)程，Pmyid表示當(dāng)前運(yùn)行程序的處理器或進(jìn)程。 算法都是在Pmyid上運(yùn)算的，處理器排序均以0 為起始，因此分成的塊也從0 起始，矩陣的行列均從1 開始，如n階矩陣A 為[a1，1… an，n]。

send 和recv 分別表示在Pmyid中的發(fā)送和接收操作。send（x，j）表示將運(yùn)行當(dāng)前進(jìn)程的Pmyid處理器中的數(shù)據(jù)x 發(fā)送給Pj處理器。recv（x，j）表示將Pj處理器中的數(shù)據(jù)x 接收到運(yùn)行當(dāng)前進(jìn)程的Pmyid處理器中。

因此在子塊 移 動(dòng) 的實(shí)現(xiàn)為順序 為Send （Ai，j，Pi，（p+i-j）modp）；Recv（Ai，j，P（i+j）modp）；即 先 把 本 處 理 器 中 計(jì) 算 出 的 數(shù) 據(jù) 循 環(huán) 向前移動(dòng)到第i 個(gè)位置處理器的內(nèi)存PING 中， 再接收循環(huán)向后第i 個(gè)位置處理器的數(shù)據(jù)放到本地內(nèi)存的PONG 中[5]。 在Epiphany 芯片中的實(shí)際操作如圖4 所示。

圖4 子塊在多核間移動(dòng)Fig. 4 Sub-block mobile between multicore

6 實(shí)驗(yàn)與結(jié)果分析

通過(guò)計(jì)算兩個(gè)512*512 大小的矩陣乘積來(lái)測(cè)試該算法。分別使用在雙核AMD 處理器的臺(tái)式機(jī)， 和單核的Epiphany芯片上，使用串行算法；以及在16 核的Epiphany 芯片在上運(yùn)行優(yōu)化后的并行程序， 來(lái)計(jì)算相同的512*512 矩陣乘法，每組進(jìn)行10 次實(shí)驗(yàn)得到數(shù)據(jù)如下：

通過(guò)表格中的數(shù)據(jù)可以發(fā)現(xiàn)：

與在標(biāo)準(zhǔn)臺(tái)式電腦上得到的結(jié)果相比較，我們看到基于Epiphany 系統(tǒng)的巨大優(yōu)勢(shì)——在一個(gè)負(fù)載平衡的系統(tǒng)中和采用更低的時(shí)鐘頻率，運(yùn)算速度卻可以提高5 倍以上。

表1 計(jì)算矩陣乘法耗時(shí)時(shí)間Tab. 1 Calculate matrix multiplication takes time

進(jìn)一步研究， 在基于16 核的Epiphany 芯片在上運(yùn)行的并行程序的各階段的時(shí)間花費(fèi)，測(cè)量時(shí)間如下：

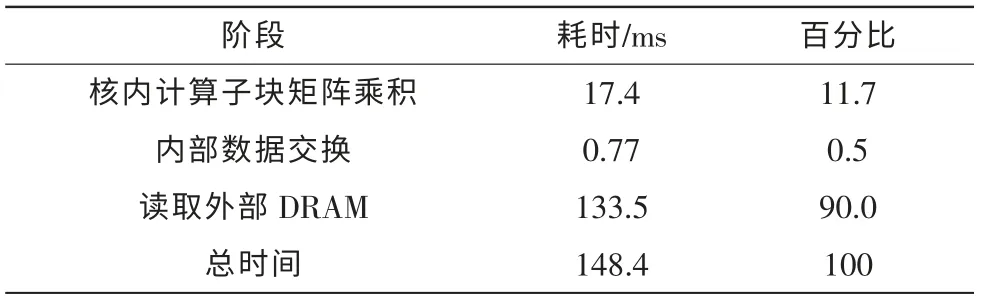
表2 并行算法各階段的耗時(shí)Tab. 2 Every stage of the parallel algorithm’s time-consuming

通過(guò)表格中的數(shù)據(jù)可以發(fā)現(xiàn)：

1）總時(shí)間并不等于各項(xiàng)時(shí)間的和，在并行運(yùn)算在多核上的性能會(huì)更低些。

2） 只有大約10%的時(shí)間是用來(lái)做真正的矩陣乘法運(yùn)算的，其余時(shí)間都用來(lái)進(jìn)行對(duì)DRAM 的讀寫。

7 結(jié)束語(yǔ)

本文在分析矩陣乘法的串行算法的基礎(chǔ)上，找出了影響其計(jì)算效率的問(wèn)題，給出了通過(guò)并行計(jì)算來(lái)實(shí)現(xiàn)可擴(kuò)展的大矩陣乘法的Cannon 算法， 以此來(lái)提高大矩陣乘法的計(jì)算效率。Cannon 算法在多核并行計(jì)算矩陣乘法中具有廣泛的應(yīng)用性[6]。

[1] 李曉梅，吳建平. 數(shù)值并行算法與軟件[M]. 北京：科學(xué)出版社，2007.

[2] 廖曉鐘，賴汝. 科學(xué)與工程計(jì)算[M]. 北京：電子工業(yè)出版社，2003.

[3] Yaniv Sapir. Scalable Parallel Multiplication of Big Matrices[EB/OL].（2013-06）[2015-03].http://www.adapteva.com/wpcontent/uploads/2012/10/Scalable -Parallel -Multiplication -of-Big-Matrices.pdf.

[4] 姜弘道，張健飛. 工程科學(xué)中的高性能計(jì)算[D]. 北京:科學(xué)出版社，2013.

[5] Adapteva， Inc. Approaching Peak Theoretical Performance with Standard C [EB/OL].（2013-06）[2015-03].http://www.adapteva.com/white-papers/approaching-peak-theoreticalperformance-with-standard-c/.

[6] 李小洲， 李慶華. 矩陣相乘cannon并行算法在工作站機(jī)群上的實(shí)現(xiàn)[J]. 計(jì)算機(jī)工程，2002（6）:102-130.