基于GA-SVM 的帶鋼表面缺陷模式識別

陳 功， 苗 瑞， 張 潔

（上海交通大學(xué) 機(jī)械與動力工程學(xué)院， 上海 200240）

模式識別即模式分類，旨在研究在原始樣本數(shù)據(jù)中尋找一種區(qū)分不同種類對象的客觀規(guī)律，依據(jù)規(guī)律構(gòu)建一個分類器，實現(xiàn)對新的樣本不同種類對象的自動歸類。 隨著社會的高速發(fā)展，我國對帶鋼的需求量不斷增大，然而由于加工環(huán)境，加工工藝，設(shè)備等原因，帶鋼表面在生產(chǎn)工程中容易出現(xiàn)諸如擦傷，輥印，銹斑，麻點等各種缺陷[1]。 對上述不同種類的缺陷進(jìn)行模式識別，有助于分析各類缺陷成因，改進(jìn)生產(chǎn)參數(shù)，所以是十分必要的。

對于帶鋼缺陷的模式識別主要包括圖像采集， 特征提取，圖像分類識別幾個步驟。 其中圖像分類識別作為其中一個關(guān)鍵技術(shù)，長久以來沒得到良好的解決。 圖像分類識別是對圖像信息，如灰度，紋理等特征參數(shù)建立機(jī)器規(guī)則，使得機(jī)器可以自動快速地對缺陷進(jìn)行歸類。 圖像識別的常用方法包括統(tǒng)計模式識別方法、人工神經(jīng)網(wǎng)絡(luò)以及基于核機(jī)器學(xué)習(xí)的方法等。 其中以支持向量機(jī)（SVM）作為模式識別的工具被廣泛采用，SVM 對于小樣本、非線性、高維模式的識別中具有很大優(yōu)勢，廣泛用于文本識別[2]，DNA 分析[3]，面部識別[4]等領(lǐng)域。

傳統(tǒng)的支持向量機(jī)或者針對某類樣本進(jìn)行優(yōu)化的支持向量機(jī)如果直接用于帶鋼表面缺陷分類時，往往會出現(xiàn)泛化性能差，過度學(xué)習(xí)，識別率低等問題。 本文采用了遺傳算法（Genetic Algorithm，GA）對SVM 進(jìn)行優(yōu)化，系統(tǒng)研究了將遺傳算法與SVM 方法結(jié)合起來用于帶鋼表面缺陷分類的過程，采用加州大學(xué)歐文分校（UCI）標(biāo)準(zhǔn)數(shù)據(jù)庫提供的真實生產(chǎn)數(shù)據(jù)進(jìn)行方法驗證， 并且與傳統(tǒng)SVM 以及BP、LVQ 神經(jīng)網(wǎng)絡(luò)、ID3 決策樹進(jìn)行比較研究，從而對帶鋼表面分類問題中GA-SVM 方法的應(yīng)用進(jìn)行科學(xué)評價。

1 算法原理

1.1 支持向量機(jī)（SVM）

支持向量機(jī)的原理是找到一個分類超平面作為決策曲面，最大化正例和反例的隔離邊緣。 支持向量機(jī)基于結(jié)構(gòu)風(fēng)險最小化的原則，不利用領(lǐng)域內(nèi)部問題，在分類問題上具有良好的泛化性能。 支持向量機(jī)有著通用性強(qiáng)，魯棒性高，計算簡單等優(yōu)點。 具體形式如下：

其中為核函數(shù)，對于徑向基核函數(shù)（RBF）：

構(gòu)造決策函數(shù)：

以上模型是二分類器，本文通過一對一法實現(xiàn)將二分類器構(gòu)造為多分類器，即對于樣本中任意兩種類別均構(gòu)造一個兩分類器，這樣共有個兩分類器，對某個樣本分類時選取所有二分類器分類結(jié)果最多那個類別作為該樣本的類別。

1.2 遺傳算法（GA）

遺傳算法（Genetic Algorithm，GA）[5-6]是模仿自然界生物遺傳進(jìn)化過程中“物競天澤，適者生存”的原理，開發(fā)出的一種全局優(yōu)化隨機(jī)搜索算法。 該算法由J.Holland 教授于1975年提出，具有應(yīng)用廣泛，使用簡單，魯棒性強(qiáng)等特點。 它借用了生物遺傳學(xué)的觀點，通過自然選擇、交叉、變異等遺傳操作，實現(xiàn)各個體適應(yīng)性的提高。 算法擁有一群個體組成的種群每個體在種群演化過程中都被評價優(yōu)劣并得到其適應(yīng)值，個體在選擇、交叉以及變異算子的作用下向更高的適應(yīng)度進(jìn)化以達(dá)到尋求問題最優(yōu)解的目標(biāo)。

2 建立GA-SVM 仿真模型

2.1 GA-SVM 模型的確定

傳統(tǒng)的SVM 也可用作分類器， 然而由于無法確定相關(guān)參數(shù)的最優(yōu)取值，所以分類效果不理想。 利用GA 對SVM 進(jìn)行優(yōu)化，主要優(yōu)化式（2）中的懲罰參數(shù)C 和式（3）中的核函數(shù)參數(shù)，確定這兩個參數(shù)的取值，從而使SVM 分類器具有較高準(zhǔn)確率。 傳統(tǒng)的網(wǎng)格搜索優(yōu)化法運行時間長，搜索效果不好，本文利用GA 算法對這兩個參數(shù)進(jìn)行優(yōu)化，采用10 折交叉驗證法下的SVM 分類準(zhǔn)確率作為遺傳算法函數(shù)適應(yīng)度值，這樣可以有效地避免過度學(xué)習(xí)和欠學(xué)習(xí)的發(fā)生，結(jié)果具有說服性。在GA-SVM 模型中，每個粒子對應(yīng)一組C、g 的取值，算法的基本步驟如下：

1）讀取樣本數(shù)據(jù)并進(jìn)行預(yù)處理，采用10 折交叉驗證法將樣本分組，初始化種群；

2）對于當(dāng)前取值的C、g，利用訓(xùn)練集進(jìn)行模型訓(xùn)練，并記錄該C、g 下的適應(yīng)度函數(shù)；

3）進(jìn)行組合交叉，變異操作，進(jìn)一步搜尋更佳的C、g 取值；

4）重復(fù)步驟2、3，直到滿足最大進(jìn)化代數(shù)。

2.2 GA-SVM 模型優(yōu)化仿真

本文采用UCI 數(shù)據(jù)庫提供的帶鋼表面缺陷數(shù)據(jù)，該數(shù)據(jù)集來自實際生產(chǎn)， 將帶鋼表面缺陷分為7 類典型的缺陷，分別為斑點，氣刀縱痕，氣刀斜痕，亮點，粗渣粒和凸起以及其他缺陷。該數(shù)據(jù)集共有1 941 組樣本，對缺陷圖像提取了包括灰度直方圖，紋理特征，投影量，圖形狀4 類共27 種特征。

模型仿真利用林智仁教授開發(fā)的LibSVM 工具箱， 使用Matlab 軟件進(jìn)行遺傳算法優(yōu)化支持向量機(jī)模型的建立和訓(xùn)練。 遺傳算法的參數(shù)設(shè)置如下：種群數(shù)量為20，交叉概率為0.7，交換表一概率為0.8，反轉(zhuǎn)變異概率為0.3，新增概率為0.3，最大進(jìn)化600 代，核函數(shù)選擇徑向基（RBF），得到SVM最優(yōu)懲罰參數(shù)C=3.73419，最優(yōu)核函數(shù)參數(shù)g=0.3657。 將此參數(shù)用于數(shù)據(jù)集的訓(xùn)練和分類， 采用10 折交叉驗證法下的分類的結(jié)果如表1 所示。

從表1 中可以看到，GA 優(yōu)化SVM 分類器的分類準(zhǔn)確性大多維持在80%以上，第7 個缺陷類別由于代表了其他缺陷類別因而分類準(zhǔn)確率較低。

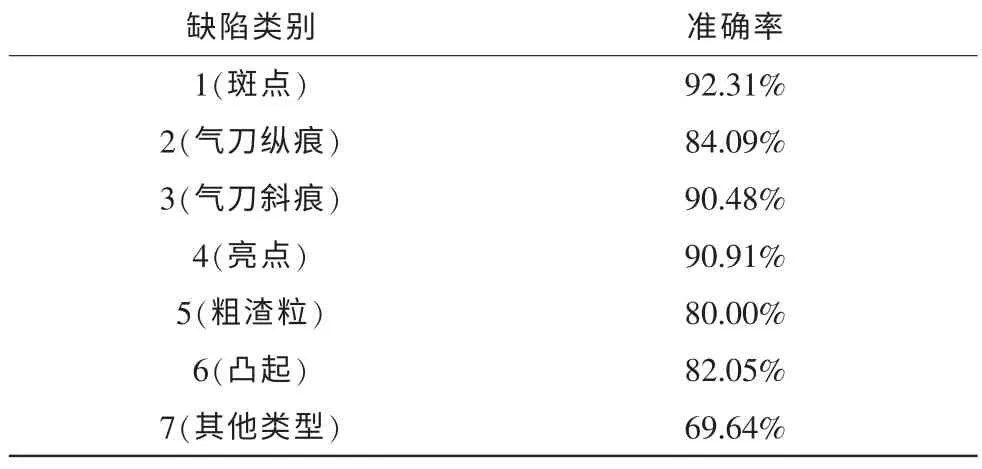
表1 分類準(zhǔn)確率表Tab. 1 Classification accuracy rate

3 結(jié)果分析

為了進(jìn)一步驗證遺傳算法優(yōu)化支持向量機(jī)的優(yōu)越性，將GA-SVM 方法與傳統(tǒng)SVM 分類器進(jìn)行對比， 分析GA-SVM方法的優(yōu)越性。 傳統(tǒng)SVM 分類器采用在[0，100]的范圍內(nèi)隨機(jī)生成的參數(shù)C、g，對比結(jié)果見圖1。

圖1 隨機(jī)參數(shù)與GA-SVM 優(yōu)化參數(shù)準(zhǔn)確率對比圖Fig. 1 Classification accuracy rate of PSO-SVM and SVM with random parameters

圖1 中黑色折現(xiàn)代表經(jīng)過遺傳算法優(yōu)化的支持向量機(jī)分類器對于每一類缺陷的分類準(zhǔn)確率，方塊，圓形，三角符號代表的數(shù)據(jù)分別表示三組隨機(jī)生成參數(shù)的SVM 分類準(zhǔn)確率，隨機(jī)得到的參數(shù)分別為第一組：C=70.6046，第二組：g=3.1833；C=19.2837，g=2.0756； 第三組：C=54.7216，g=13.8624。所有仿真實驗數(shù)據(jù)均采用10 折交叉驗證法得出分類準(zhǔn)確率。 可以明顯看出， 雖然有個別隨機(jī)參數(shù)的缺陷準(zhǔn)確率比GA-SVM 高，但是這些個別的高準(zhǔn)確率實際上是由于判別樣本少造成的。整體來看GA-SVM 的準(zhǔn)確率大都保持在80%以上，可見本文采用遺傳算法對支持向量機(jī)分類器進(jìn)行優(yōu)化是有效的。

圖2 所示為GA-SVM 與其他三種常用算法的分類準(zhǔn)確率比較。 比較的對象分別為BP 神經(jīng)網(wǎng)絡(luò)，LVQ 神經(jīng)網(wǎng)絡(luò)和ID3 決策樹算法， 對比各算法對于每一缺陷類別的分類準(zhǔn)確率， 依舊采用10 折交叉驗證法下的分類準(zhǔn)確率。 圖2 中可見，經(jīng)過遺傳算法優(yōu)化的支持向量機(jī)分類器的分類準(zhǔn)確率相較其他三種算法更高， 平均分類準(zhǔn)確率達(dá)到83.62%， 而BP神經(jīng)網(wǎng)絡(luò)，LVQ，ID3 的平均分類準(zhǔn)確率分別為63.09%、74.90%、70.36%。由此可見，GA-SVM 模型能夠更準(zhǔn)確地對缺陷類型進(jìn)行分類預(yù)測，對于帶鋼表面缺陷分類問題，GA-SVM方法相較其他方法具有一定的優(yōu)越性。

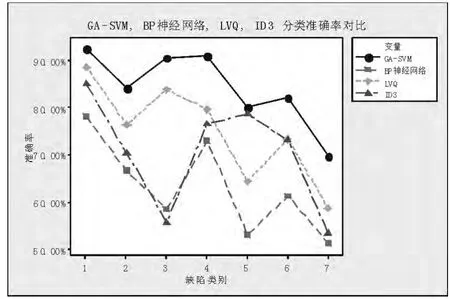
圖2 4 種算法分類準(zhǔn)確率對比Fig. 2 Classification accuracy rate of four kinds of algorithms

4 結(jié)束語

帶鋼表面缺陷的準(zhǔn)確分類，是帶鋼在線檢測技術(shù)的重要環(huán)節(jié)。 傳統(tǒng)分類方法在處理多分類問題時有一定局限性。SVM 算法具有很強(qiáng)的非線性建模能力，主要根據(jù)所提供的生產(chǎn)數(shù)據(jù)，通過學(xué)習(xí)和訓(xùn)練找到輸入數(shù)據(jù)與輸出數(shù)據(jù)之間的潛在關(guān)聯(lián)，從而對新樣本進(jìn)行預(yù)測。 本文將遺傳算法與支持向量機(jī)相結(jié)合， 采用10 折交叉驗證法下的分類準(zhǔn)確率作為遺傳算法適應(yīng)度，充分發(fā)揮了SVM 方法的非線性建模能力，同時規(guī)避了隨機(jī)設(shè)定SVM 參數(shù)的盲目性， 提高了模型的泛化能力。 通過與傳統(tǒng)SVM 分類器以及其他分類算法的比較，GA-SVM 對于帶鋼表面缺陷多分類問題效果更優(yōu)。

[1] 魏 烈 省. 冷軋鋼帶表面缺陷分析[J]. 鋼鐵，2006，41（2）:386-388.

WEI Lie-sheng. Analysis of surface defects of cold rolled steel strip[J]. Iron and Steel，2006，41（2）:386-388.

[2] 高學(xué)，金連文.一種基于支持向量機(jī)的手寫漢字識別方法[J].電子學(xué)報，2002，30（5）:484-487.

GAO Yue，JIN Lian-wen. A handwritten Chinese character recognition method based on support vector machine [J].Electronic Journal，2002，30（5）:484-487.

[3] A Zien，G Ratsch，S Mika，et al. Engineering supportvector machine kernels that recognize translation initiation sites[C]//Bioinformatics，2000，16（9）:799.

[4] Y Li，S Gong，J Sherrah，et al. Support vector machine based multi-view facedetection and recognition[J]. Image and Vision Computing，2004，22（5）:413-427.

[5] JHHolland. Ada Ptationin Natural Artifieial Systems [M].MITPress，1975:1-17.

[6] 黃少榮. 遺傳算法及其應(yīng)用[J]. 電腦知識與技術(shù)，2008，4（7）:1874-1875.

HUANG Sao-rong. Genetic algorithm and its application[J].Computer Knowledge and Technology，2008，4（7）:1874-1875.