近岸波生環流的三維數值模擬研究

王平，張寧川

(1.國家海洋環境監測中心，遼寧大連116023;2.大連理工大學海岸和近海工程國家重點實驗室，遼寧大連116023)

在近岸區域隨著水深的變淺，潮動力逐漸減弱，波生沿岸流和波生環流則成為近岸主要的水動力因素。根據Longuet-Higgins等［1］的研究，波浪在傳播和破碎的過程中會引起剩余動量流稱之為輻射應力，這一動量的存在影響流體的運動，引起波浪增減水及波生流，其形態包括平面以及垂向環流。早期的水動力模型在研究波浪對潮流的影響時，大都采用沿深度均布的輻射應力公式［2］，可研究波生流的平面分布，對其三維結構研究較少。為此，Zheng等［3］提出了笛卡爾坐標系下沿水深分布的輻射應力計算公式，Xia等［4-5］分別提出了σ坐標系下的三維輻射應力公式，但是基于上述三維輻射應力理論的三維波生流模型的研究較少。謝鳴曉［6］基于沿深度分布的輻射應力理論建立了三維波生流模型，但并未系統研究其機理，且模型基于結構化網格計算;佟飛飛等［7］分別建立了基于曲線網格下波生流模型，但未考慮三維輻射應力的影響，Wang等［8］基于非結構化網格構建了三維波流耦合模型，但并未系統研究近岸波生環流的機理問題。因此，本文基于沿深度變化的三維輻射應力計算公式，在水動力模型的基礎上建立了波生流三維數值計算模型，模型考慮波浪紊動效應，以及波流共同作用下的表面和底部切應力。模型基于非結構化網格離散，較結構化網格在近岸復雜區域的擬合精度更高，且可對重點區域進行加密計算。模擬了由于近岸地形及岸線變化形成的波生平面環流、沿岸流，以及斜坡地形上波浪破碎引起的垂向環流，并同實驗數據進行對比，驗證了模式精度和通用性。

1 波生流三維模型的建立

1.1 控制方程

水動力模型采用FVCOM模式，控制為在ζ坐標系下的三維Navier-Stokes方程組，同時引入波生三維時均剩余動量和紊動摻混效應對水體的影響。

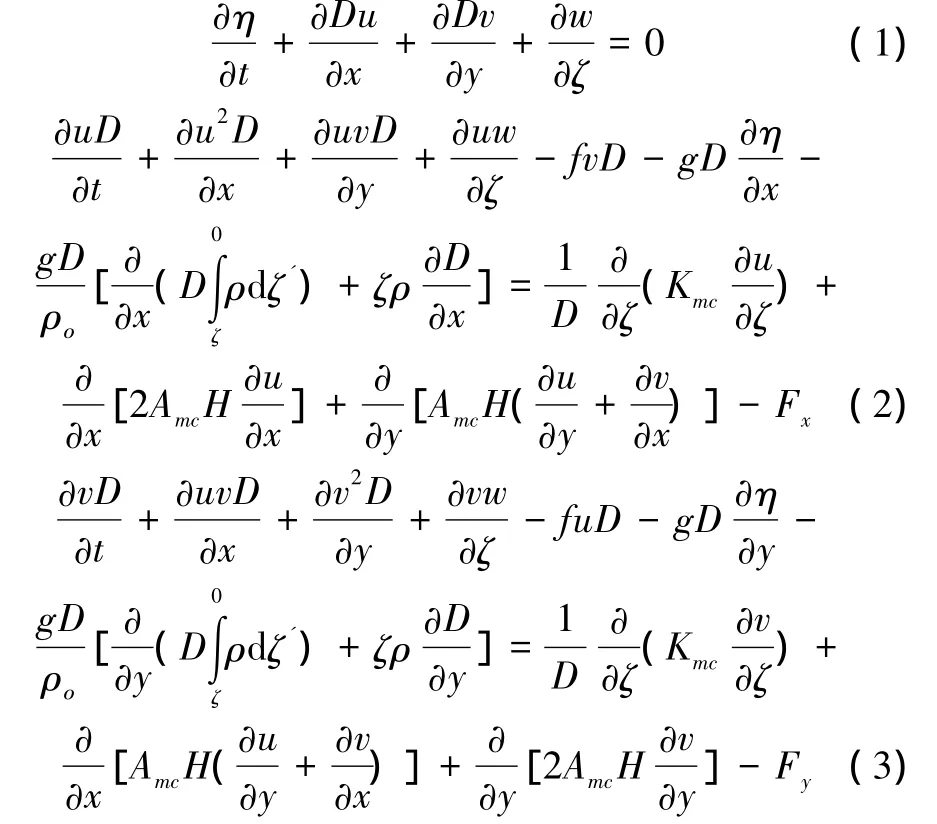
式中:η為自由水面;x和y為水平坐標;ζ=(z-η)/D為轉換后的垂向坐標;w為ζ坐標系下的垂向流速分量;u和v為水平流速分量;Kmc為波流共存的垂向紊動粘性系數;Amc為波流共存的水平紊動粘性系數;F為波浪輻射應力項。

對波流共同作用下的紊動系數采用文獻［6］的方法，即分別單獨求解水流與波浪引起的紊動系數A和K，再將其線性疊加，可表述為

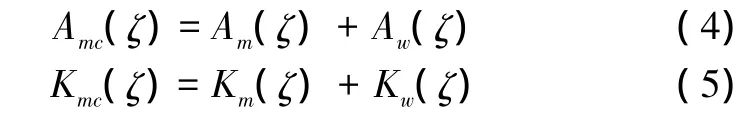
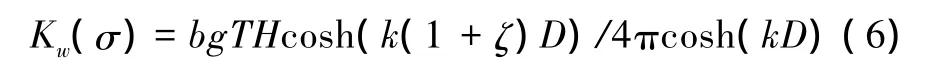
水流引起的水平紊動系數采用Smagorinsky公式:

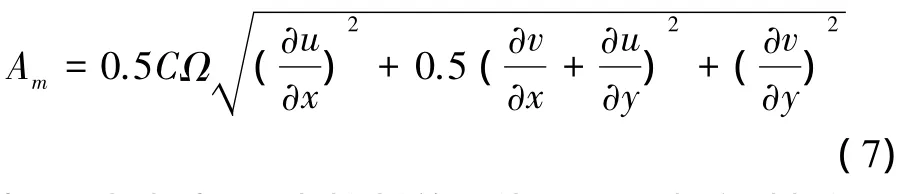
式中:C為常速;Ω為控制單元體面積。水流引起的垂向紊動系數Km采用Mellor-Yamada紊流閉合模型求解。

1.2 邊界條件

根據Signell［9］簡化波流相互作用模式，得到波流聯合作用下底部切應力可寫為

式中:τc為流作用下的底應力;τw為波浪作用下的最大底應力，，U0為波浪近底最大流速，U0=Aσ/sinhkh，A為波浪振幅;fw為波浪摩擦參數，可由半經驗公式(9)迭代求出:

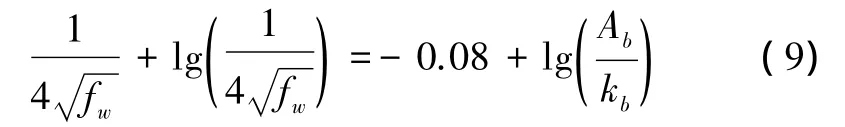
式中:kb=30z0，z0為底粗糙參數;Ab=U0/ω。

根據τw可求得波浪摩阻流速，流作用下的底應力可以寫為，F=B1/2fcρu(u2+v2)1/2，GB=1/2fcρv(u2+v2)1/2，流摩擦系數fc可寫為

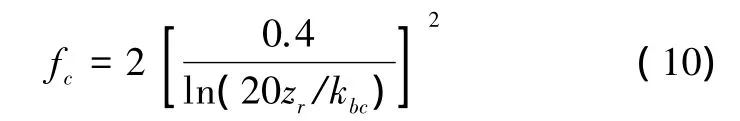
式中:zr為計算點與海底的距離不考慮波浪對流影響時，kbr=kb=30z0，流的摩阻流速，波流相互作用下總的摩阻流速則為

通過調查學生聽、說、讀、寫四大語言技能發現，81%的學生表示可以看懂并寫出英語。 但對于聽說，尤其是聽的技能，54%的學生表示完全聽不懂英美原聲廣播或電視節目； 32%的學生能聽懂部分內容； 其余則表示不確定能否聽懂。 這一現象說明： 日常大學英語側重讀寫技能，而忽視聽說技能，尤其是真實語境中聽說能力的訓練。 這嚴重割裂了語言與社會及文化的關系，學生只習得目的語的詞匯、語法系統，構建了詞匯-語法潛勢。 但無法了解到伴隨的副語言系統，如肢體語等非語言交際，因而缺乏行為潛勢和意義潛勢的培養，這一現象嚴重影響了學生跨文化交際能力的培養。

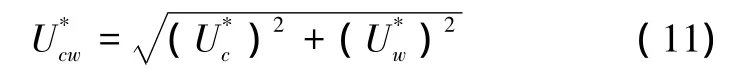
1.3 輻射應力項計算

本文采用波浪輻射應力隨深度變化的Zhang［5］公式，具體形式為

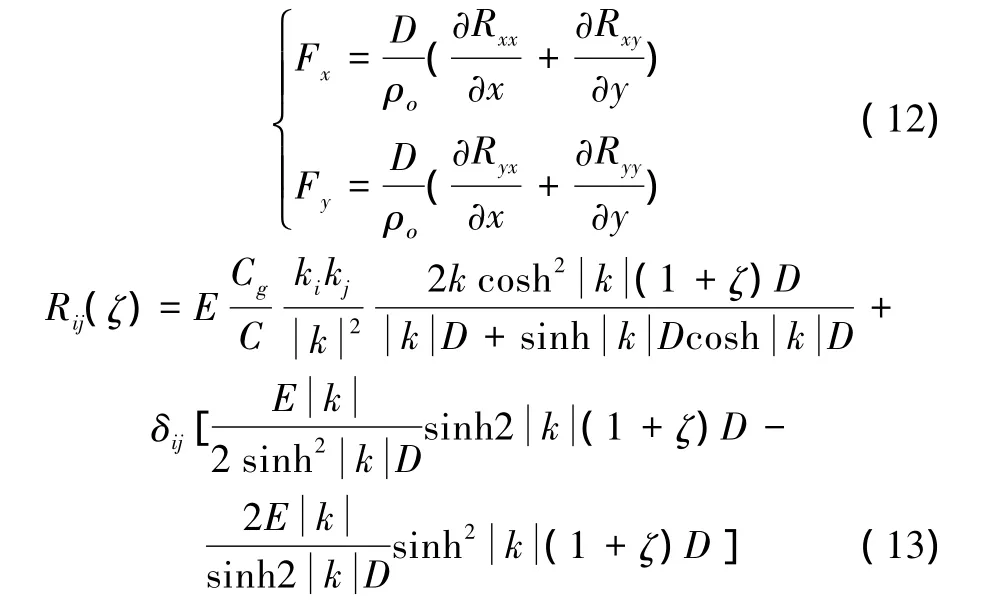
式中:E為波能;k為波數;δ為克羅內爾標記;i、j分別代表x，y方向。

1.4 離散方法

波生流模型基于非結構化網格離散，方程求解采用內外模態分離法，外模求解采用顯式方法，內模采用隱式求解。參量η、D、w、ρ、q2、q2l、KM、KH、AM、AH和Rij在三角形節點上計算，而u和v則基于三角形中心。對控制方程在空間上沿控制體積分，并利用格林公式得到沿控制體邊的離散形式;時間上差分采用二階精度的Runge-Kutta積分格式離散。波浪近岸增水會引起漫灘，動邊界采用干濕網格法處理。

2 模式驗證及研究

2.1 斜坡上三維環流

波浪傳播到近岸破碎帶時會發生底部離岸流現象，在破波帶內表層水體向岸流動，為達到水體平衡，底部水體發生離岸運動，從而形成回流。Okayasu等［10］研究了造成這一現象的主要原因是輻射應力分布表層大于底部而形成的。Ting［11］利用波浪水槽進行了多次試驗，研究了斜坡上的底部離岸流特征。

試驗用的水槽長40 m，地形坡度為1∶35;造波機處的水深為0.4 m;入射波高為0.127 m;周期為 2 s;模型垂向分成30層;網格步長為0.05 m;時間步長為0.01 s。模型計算的破波點發生在離岸邊6.4 m處，與試驗結果相同。

計算得到輻射應力隨深度增加逐漸減小，見圖1，L為點離岸線的距離。表層和底層輻射應力沿波浪傳播方向的變化見圖2，其中表層為數值σ層中第一層、底層為第30層。

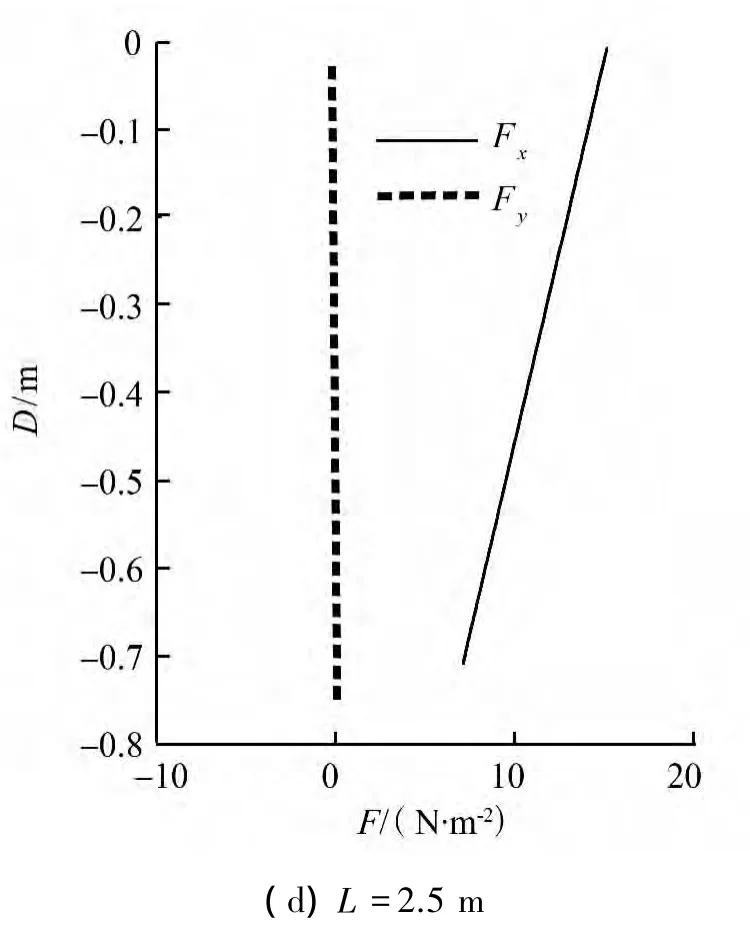
圖1 輻射應力在不同位置處的沿深度分布Fig.1 Vertical profile of radiation stresses in different water depths

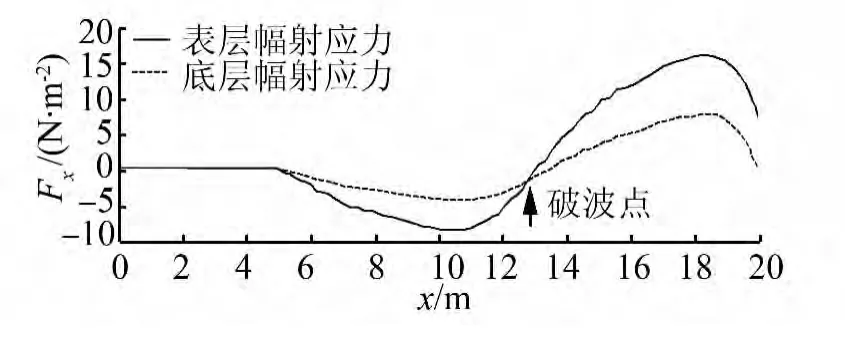
圖2 表層和底層輻射應力的平面分布Fig.2 Horizontal profile of radiation stresses in surface and bottom

模擬得到的底部離岸流的垂向分布結構見圖3，從圖中得到計算區域內存在2個垂向環流，在破碎帶內表層水體向岸流動，底層水體離岸流動。

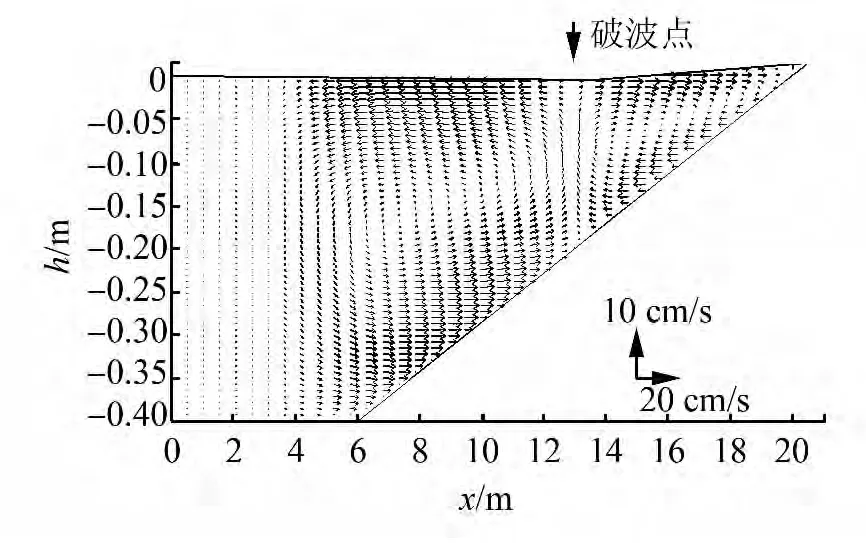
圖3 破波帶內外垂向環形流場Fig.3 Wave-induced circulation inside and outside the surf zone

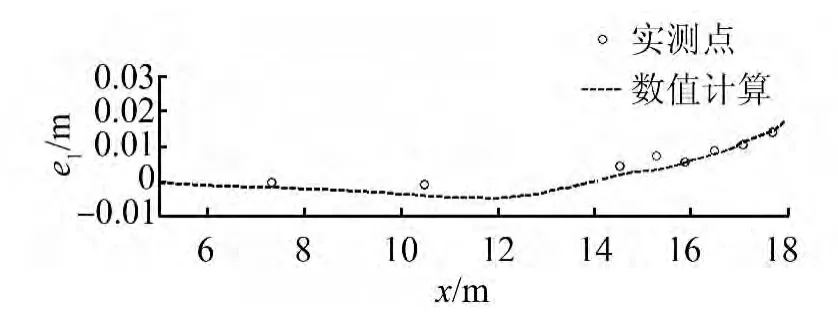
圖4 增減水對比圖Fig.4 Comparison of wave set-up and set-down

而在破波帶外，受輻射應力變化與破碎帶內的趨勢相反，故其表層水體離岸流動，底層水體向岸流動，這一流場特征和 Zhang［5，12］描述的相同。計算得到波浪增減水結果及驗證見圖4，試驗實測的8個點的垂向流速分布與模型計算結果對比見圖5。

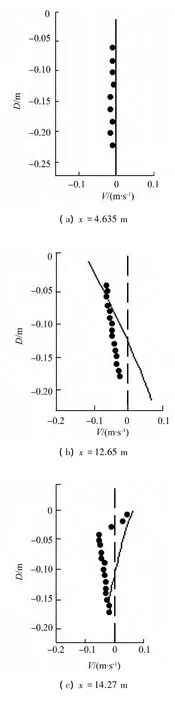
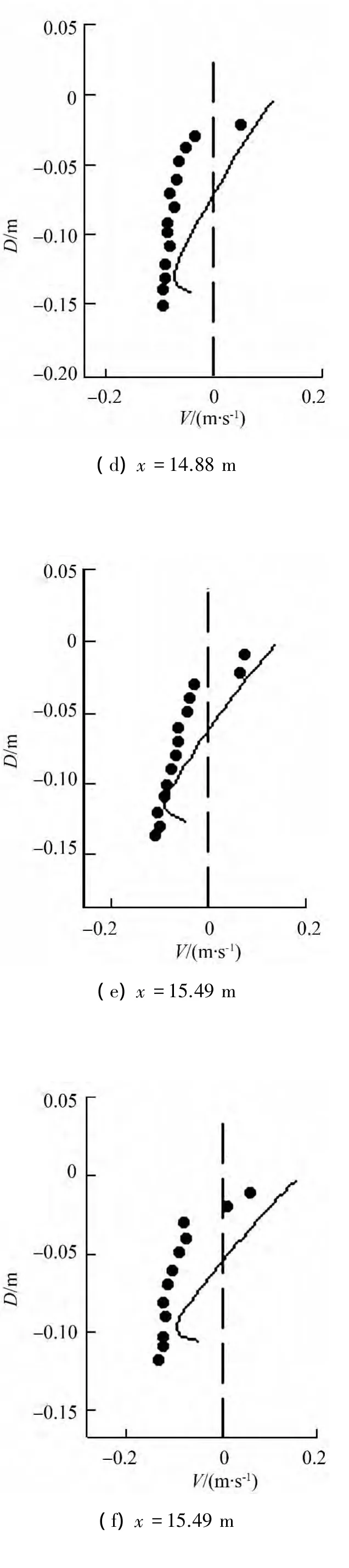
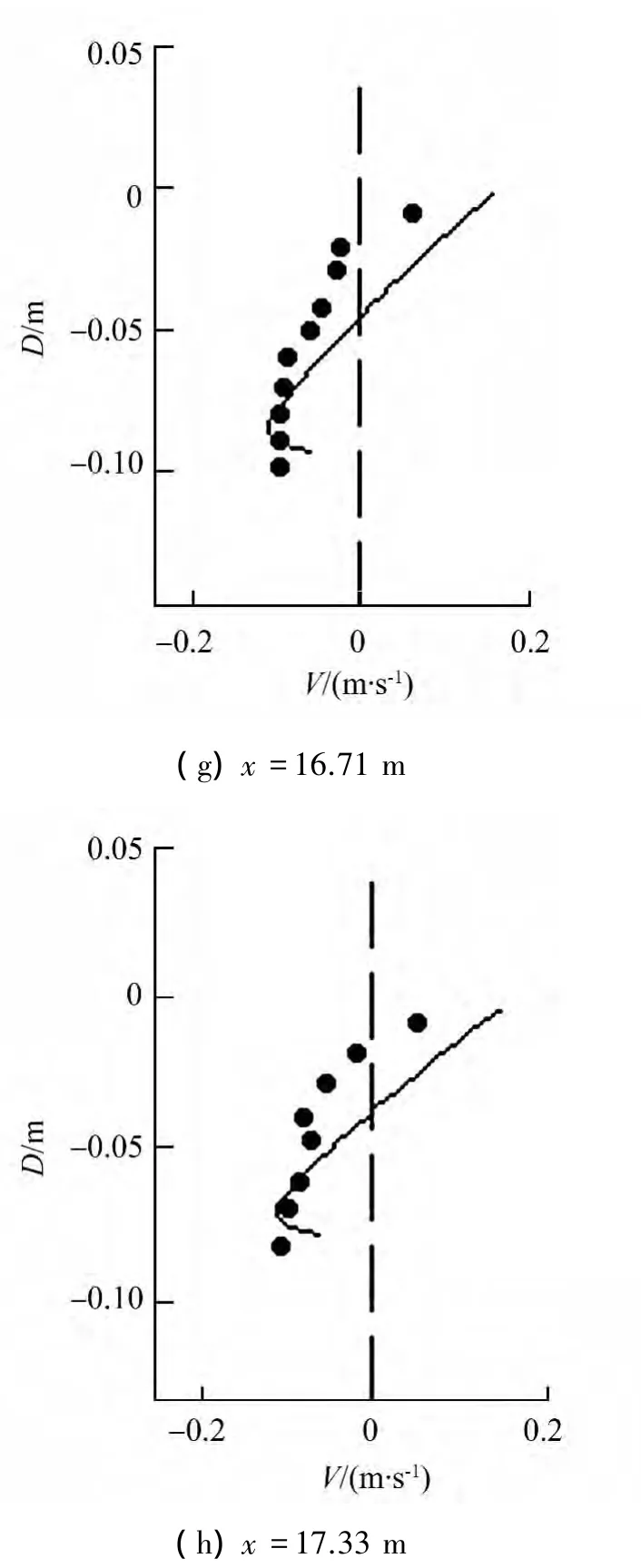
圖5 不同位置處的垂向流速驗證Fig.5 Verification of the vertical velocity in different locations

2.2 人工島后的波生環流

波浪傳播過程中遇到人工島等障礙物時，會在人工島后發生繞射;由于波浪繞射形成島后波影區剩余動量的各向梯度，從而會形成島后環流現象。日本東京電力研究所實驗研究了人工島內側取水口周圍波浪場以及波浪破碎引起的波生流［13］。

試驗中人工島布置在坡度為1∶50的斜坡上，整個實驗區域長為 23.5 m，寬為 19.2 m;人工島大小為 6.6 m×3.3 m。模型計算時計算域選取19.2 m×15.0 m，入射波高為 0.03 m，周期為 1.0 s，波浪破碎指標選為0.76，流場底摩擦系數選為 0.025。

圖6中給出實驗得到的波生流實測流場分布，表1給出了A-J10個點的平均流場實測值和計算值對比。圖7給出了波生流模型的計算網格，圖8為模型模擬得到的平均流場分布。

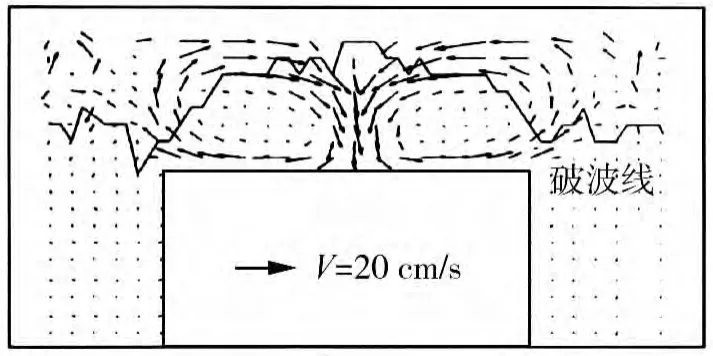
圖6 人工島后實測波生流場(規則波，H=4.22 cm，T=1.06 s)Fig.6 The measured wave-induced flow field behind artificial island(regular wave，H=4.22 cm，T=1.06 s)

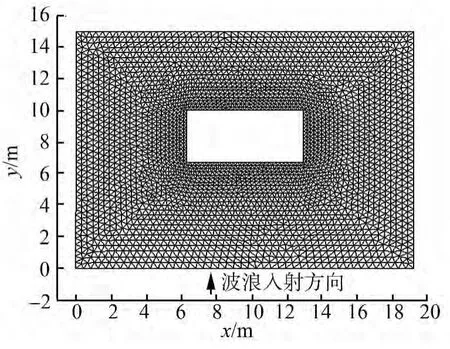
圖7 模型計算網格Fig.7 The computational mesh

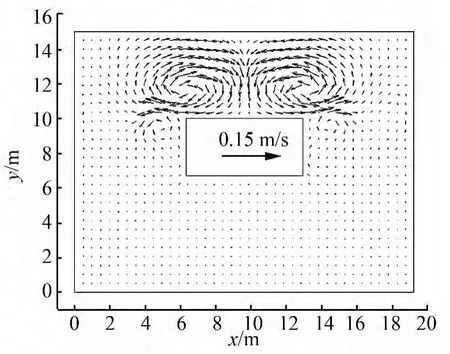
圖8 波生流場計算結果Fig.8 The simulated wave-induced flow field

表1 浮式風機模型主尺度Table 1 Main scale of the model

根據對比可以看出本模型流場流速的數值解和實測值比較接近;模擬得到在人工島內側的對稱軸附近產生了回流現象，同時在島內側區域形成一對方向相反的環流，該形態和實測得到人工島后的波生流結果一致。

2.3 正弦波狀地形下的裂流

實際海灘剖面在沿岸方向是不規則變化的，這種地形的沿程不均勻會導致裂流及沿岸流的出現。Borthwick等［14］研究了正弦波狀地形下、不同入射角度的波生流結構。數值計算中，波浪入射波高為0.125 m，波周期1.2 s。波浪分別按沿x軸正向、偏離x軸5°和20°斜向下入射3種工況計算。

數值計算地形見圖9(a)，計算得到波浪正向入射后的垂向平均流場見圖9(b)，實測平均流場見圖9(c);斜向5°入射后的流場見圖10(a);斜向20°入射后的流場見圖10(b)，實測流場見圖10(c)。從圖中可以得到，正向入射波浪傳播到近岸破碎后會形成向岸的波生流，兩股向岸流會在兩凸起中間形成裂流，進而形成平面波生環流。波浪5°斜向入射時，依然會形成裂流和波生環流，此時裂流的方向不再嚴格垂直于岸線;但當入射角度為20°后則會形成正弦狀沿岸流。與實測結果的誤差可能由于數值模式中對固邊界的近似處理造成的。

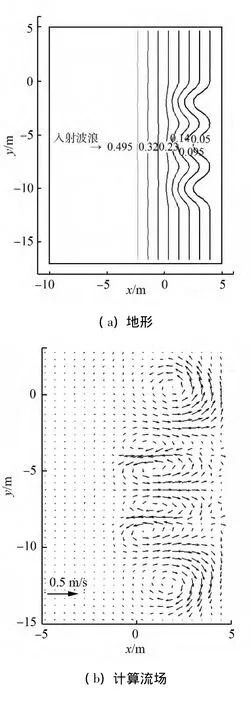
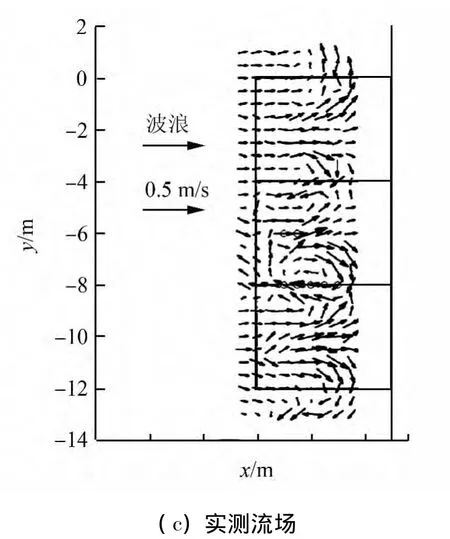
圖9 計算地形與正向入射平均流場及驗證Fig.9 Computational topography and verification of wave-induced flow field

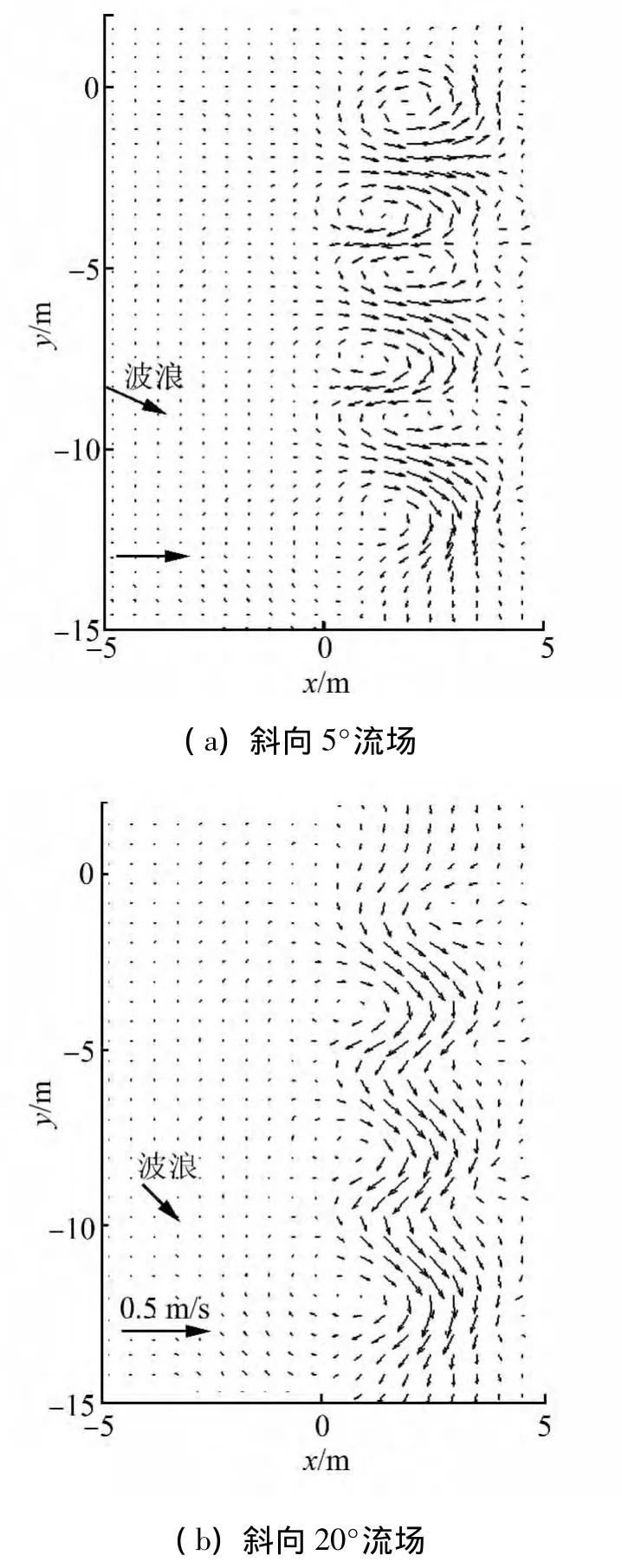
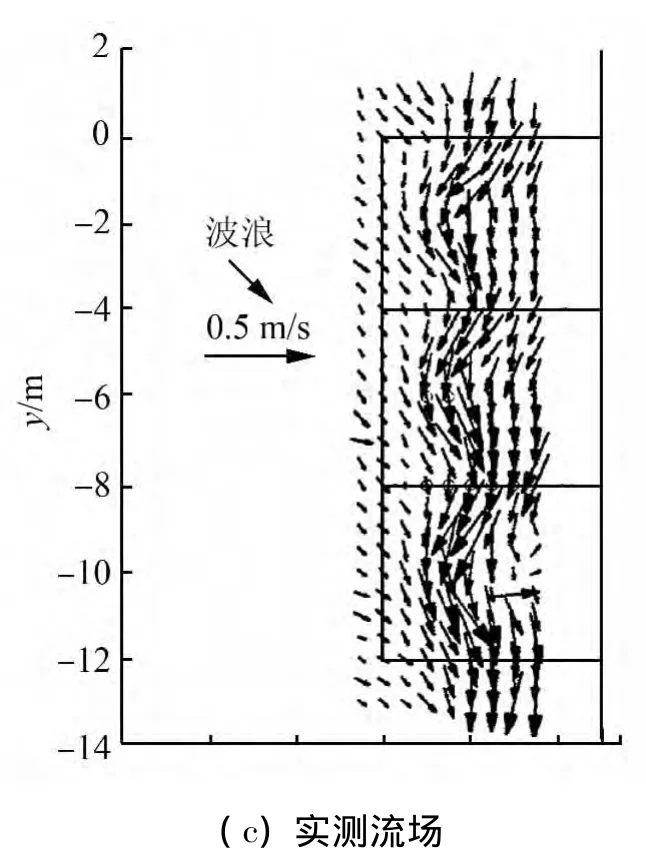
圖10 斜向入射平均流場及驗證Fig.10 Verification of flow field induced by oblique wave

3 結論

采用沿深度變化的三維輻射應力公式，建立了近岸波生流三維數值模型。數值模擬結果和實驗數據吻合很好，并得到如下結論:

1)在近岸斜坡地形上，水深變淺以及波浪破碎導致波高變化，并會引起沿平面和深度分布不均的三維輻射應力。輻射應力的分布不均會驅生兩個不同方向的垂向環流，即在破碎帶內表層水體向岸流動，底層水體離岸流動;而在破碎帶外表層水體離岸流動，底層水體向岸流動。

2)在人工島等擋浪建筑后，由于波浪繞射和破碎會引起波影區內剩余動量的各向梯度，從而驅生了平面分布的環形時均流。而在正弦波狀斜坡地形上，正向入射波浪傳播到近岸破碎后會形成向岸的波生流，并會在兩凸起中間形成裂流，進而形成平面環流。波浪小角度斜向入射時，依然會形成裂流和波生環流;但當入射角度過大則會形成正弦狀沿岸流。

［1］LONGUET-HIGGINS M S，STEWART R W.Radiation stress and mass transport in gravity waves with application to surf beats［J］.Journal of Marine Research，1962，13:481-504.

［2］GODA Y.Examination of the influence of several factors on longshore current computation with random waves［J］.Coast Eng，2006，53(2/3):157-170.

［3］ZHENG J H.Depth-dependent expression of obliquely incident wave induced radiation stress［J］.Progress in Natural Science，2007，17(9):1067-1073.

［4］XIA H Y，XIA Z W，ZHU L S.Vertical variation in radiation stress and wave-induced current［J］.Coast.Eng.，2004，51(4):309-321.

［5］ZHANG D.Numerical simulation of large-scale wave and currents［D］.Singapore:National University of Singapore，2004:10-17.

［6］謝鳴曉，張瑋.近岸波生流運動三維數值模擬及驗證［J］.水科學進展，2011，22(3):391-399.XIE Mingxiao，ZHANG Wei.3D numerical modeling of nearshore wave-induced currents［J］.Advances in Water Science，2011，22(3):391-399.

［7］佟飛飛，沈永明，崔雷.基于曲線坐標系下緩坡方程模擬近岸波浪及波生流［J］.中國科學，2011，41(2):161-169.TONG Feifei，SHEN Yongming，CUI Lei.Numerical simulation of nearshore waves and wave-induced currents based on mild-slope equation in curvilinear coordinates［J］.Scientia Sinica Phys，Mech ＆ Astron，2011，41(2):161-169.

［8］WANG J H，SHEN Y M.Development and validation of a three-dimensional，wave-current coupled model on unstructured meshes［J］.Science China G，2011，54(l):42-58.

［9］SIGNELL R P.Effect of wave-current interaction on windderived circulation in narrow，shallow embayments［J］.Geophys Res，1990(95):9671-9678.

［10］OKAYASU A，SHIBAYAMA T，HORIKAWA K.Vertical variation of undertow in the surf zone［C］//Proceedings of Coastal Engineering，ICCE，ASCE，1988，478-491.

［11］TING F C K，KIRBY J T.Observation of undertow and turbulence in a laboratory surf zone［J］.Coast Eng.，1994，24(1):51-80.

［12］NOBUOKA H，KATO H，MIMURA N.Vertical distribution of radiation stresses and 3D nearshore currents around coastal structures［C］//Proc 12th Int offshore Polar Eng Conf.Kitakyushu，Japan，2002:672-679.

［13］李紹武，柴山知也.近岸區人工島周圍波生流系統數學模型的驗證［J］.天津大學學報，1998，31(5):584-589.LI Shaowu，TOMOYA S.Verification of a wave-induced current model around nearshore artificial island［J］.Journal of Tianjin University，1998，31(5):584-589.

［14］BORTHWICK A G L，FOOTE Y L M.Nearshore measurements at a cusped beach in the UK Coastal research Facility［C］//Coastal dynamic 97 Plymouth，ASCE，USA，1997:953-962.