基于分布式ICA-PCA模型的工業過程故障監測

衷路生，何東，龔錦紅，張永賢

（華東交通大學電氣學院，江西 南昌 330013）

基于分布式ICA-PCA模型的工業過程故障監測

衷路生，何東，龔錦紅，張永賢

（華東交通大學電氣學院，江西 南昌 330013）

提出基于分布式ICA-PCA( independent component analysis-principal component analysis)模型的工業過程故障監測方法，適合于復雜工業過程難以自動劃分子塊及過程數據存在非高斯信息的情況。首先，對過程數據進行PCA分解，并在PCA主成分不同的方向上構建不同的子塊，把原始特征空間自動劃分為不同子空間。然后，對各個子塊采用ICA-PCA兩步信息提取的策略，提取出高斯信息和非高斯信息，并構建新的統計量和統計限。最后，通過Tennessee Eastman(TE)過程的仿真實驗，驗證所提出故障監測模型的有效性和可行性。

復雜工業過程；自動劃分子塊；非高斯；ICA-PCA；故障監測

獨立主元分析（ICA）由于能有效處理非高斯信息而廣泛應用在過程監測領域。Lee等[10]提出使用ICA進行統計過程監測，同時，國內學者陳國金等[11]也對此做了很多工作；而后，Lee等[12]提出動態ICA的過程監測方法；Yoo等[13]指出可使用多路ICA進行在線過程監測；最近，Ge等[14]結合集成學習算法和貝葉斯推理策略提高了ICA的監測能力；Kano等[15]首次將ICA和PCA結合在一起，將數據分為高斯部分和非高斯部分；此后，Ge等[16]提出基于ICA-PCA兩步信息提取的故障監測方法。

針對工業系統的復雜性，研究人員提出分層和分區統計的思想。MacGregor等[17]提出建立各個子塊監測診斷圖和全體監測圖，提高監測性能；Westerhuis等[18]從算法和理論角度分析了多嵌段和多層次PCA、PLS算法，指出對同一個工業過程，其結果可以用普通PCA和PLS算法計算；Cherry 等[19]在討論多嵌段PLS算法時，給出了子塊和變量對T2及SPE貢獻的新定義；Ge等[20]提出兩步多嵌段監測方法。顯然，這些方法都是利用過程知識來劃分子塊，而復雜工業過程的知識通常難以獲得。因此，它們雖然提高了每個子塊的監測能力，卻無法滿足自動劃分子塊的要求[21-22]。

基于以上分析，本文結合ICA理論提出分布式ICA-PCA模型，適合于復雜工業過程難以自動劃分子塊及過程數據存在非高斯信息的情況。首先，對過程數據進行PCA分解，獲得各自含有不重疊信息的主元，在各個主元子空間和殘差子空間上構建子塊；其次，利用過程變量對各個子塊的貢獻值選擇變量，構建互不相關的子塊空間；最后，利用ICA算法提取各個子塊的非高斯信息，對其殘差進行PCA分解，構建統計量和統計限實現工業過程監測。

1　獨立成分分析（ICA）

1.1ICA基本原理

ICA是伴隨著盲分離問題而發展起來的一種統計信號處理方法，處理對象是相互統計獨立的源信號經線性組合而產生的一組混合信號，目的是確定一個線性變換矩陣，使得混合信號變換后的輸出分量盡可能地統計獨立。假設有l個測量變量，在樣本點k處，可以表示為r個未知獨立成分[s1, s2,…,sr]T的線性組合，其中r≤l ；它們的關系如下所示[10]

ICA算法的基本原理就是在X已知的情況下，估計源信號矩陣S和混合矩陣A，其主要目的就是尋找一個分離矩陣W，可從觀測信號中分離出源信號，即

1.2獨立成分的排序和數目選取

對過程數據獨立成分分析時，若獨立成分數目選取過多，則會放大過程數據的噪聲，反之，則難以有效提取數據的非高斯信息。為了選取合適的獨立成分，本文首先根據分離矩陣 W每一行iw的歐幾里得范數對信號的貢獻大小來實現獨立成分的排序，然后借鑒 PCA方差貢獻圖的原理，繪制iw的歐幾里得范數對W的貢獻圖，采用試湊法來選取獨立成分數目[10]。

2　基于分布式 ICA-PCA模型的過程監測

本節首先利用離線正常數據建立分布式ICA-PCA的故障監測模型；其次，對于新的測試樣本，進行在線監測；最后，實現故障診斷。

2.1過程數據的子塊劃分和模型建立

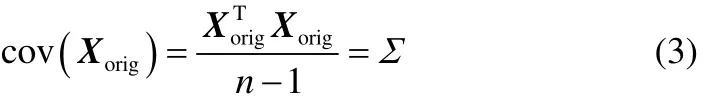
其中，origX已作歸一化處理，即均值為0，標準差為1。如果選擇k個主成分構建PCA模型，那么原始數據矩陣origX可以表示為it、ip和殘差 E的和

其中，it是得分向量，ip是載荷向量。式（4）可等價表示為

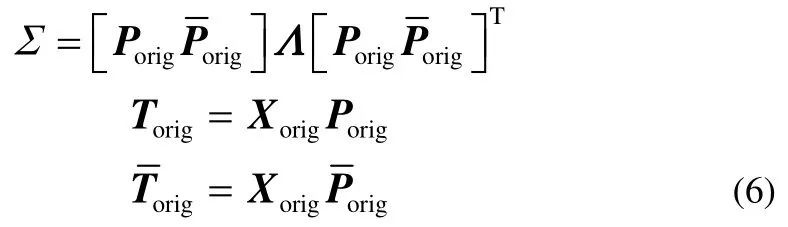
由于 PCA是在最小均方意義下尋找最能代表原始數據的投影方向，那么選擇的k個主成分彼此是不相關的。通過在每一個不相關的主成分上構建子塊，可以滿足子塊劃分的多樣性要求；在每一個不相關的子塊上選擇最相關的變量，可以滿足每一個子塊模型的精度要求。PCA模型的殘差部分與每一個主成分都不相關，因此可在殘差子空間構建一個子塊。即在過程數據中，共構建k+1個子塊。根據每個變量對各個主成分即各個子塊的貢獻值大小來選擇各子塊相應的變量[22]，具體地，所有變量對前k個子塊的貢獻值為

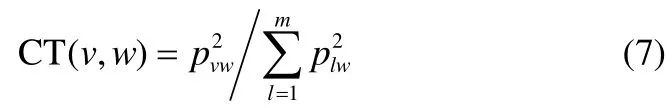
其中，v=1,2,…,m ，m為過程變量的數目；w=1,2,…,k，k為主成分數目；p為主元載荷矩陣，pvw表示該載荷矩陣在第v行、第w列的元素。

每個變量在殘差載荷矩陣所有主元上的平均值為

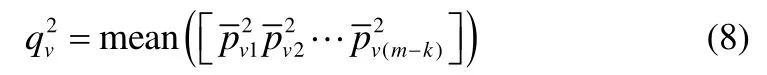
由式（8）可得所有變量對第k+1個子塊的貢獻值為

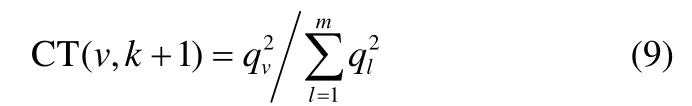
其中，v=1,2,…,m ，m為過程變量的數目；k為主成分數目，mean表示求均值。

根據式（7）、式（9），對各個子塊貢獻大的變量分別選作該子塊的變量。

根據以上構建的子塊，對每個單獨子塊構建分布式ICA-PCA模型。

首先，對每個單獨子塊Xi進行獨立成分分析，設共提取出 ri個獨立成分，則

源信號矩陣iS的估計值為

然后，對每個子塊的殘差矩陣Ei進行PCA分解

其中，i=1,2,…,k+1，Ti為每個子塊的得分矩陣， Pi為每個子塊的載荷矩陣， Fi為每個子塊的殘差矩陣。

本文通過檢測各子塊負熵值選擇獨立成分的數目：如果當前子塊的負熵值為零或接近為零，說明子塊過程數據的非高斯信息提取完全；主成分的數目可以由累計方差百分比規則（CPV）確定。

2.2基于分布式ICA-PCA模型的在線過程監測

對于一個新的數據樣本 Z，計算每個子塊的獨立成分矩陣、得分矩陣如下

其中，i=1,2,…,k+1。

構建新的統計量I2、T2和SPE[10,16]。

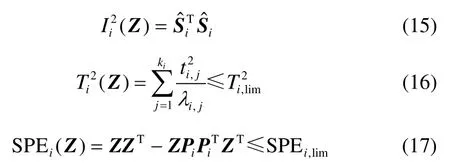
其中，i=1,2,…,k+1，ki為每個子塊選取的主成分數目，λi, j為每個子塊的特征值。

利用一維核密度估計（KDE）的方法求子塊 I2的統計限[10-11]，定義如下

其中，i=1,2,…,k+1， xi為子塊過程數據，h為窗寬或光滑參數，n為各子塊樣本數目，k為核函數。根據概率理論，核函數滿足以下條件

如果各個子塊監測圖的統計量超出了統計限，那么說明該子塊發生了故障。

2.3故障診斷

為了確定引起故障的變量，借鑒文獻[22]的思想，采用以下的故障診斷方法。

首先，把所有子塊劃分為兩部分：可監測到故障的子塊集合（FY）和無法監測到故障的子塊集合（FN）。具體定義如下

其中，u代表可監測到故障的子塊數目，v代表無法監測到故障的子塊數目，且u+v=k+1，A和B表示相應子塊集合中所包含變量的向量。

其次，求出可監測到故障的子塊所含變量的交集IVS（included variable set）和無法監測到故障的子塊所含變量的交集EVS（excluded variable set），具體定義為

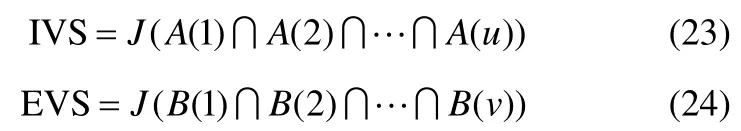
其中，J表示求所有子塊變量的交集。

最后，通過整合IVS和EVS兩個變量集合，可求得該故障的責任變量集合（responsible variable set，RVS），即

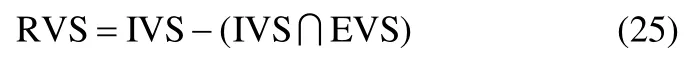
2.4監測模型效率分析

由于采集原始數據和故障測試數據的復雜性相同，因此本文從定性角度分析分布式 ICA-PCA故障監測模型的效率問題。在分布式PCA模型中，首先通過 PCA分解劃分子塊并求出可監測到故障的子塊，然后在該子塊構建傳統PCA監測模型。而分布式ICA-PCA模型是在分布式PCA模型的基礎上，增加了ICA的計算，即式（10）和式（11），因此分布式 ICA-PCA模型的效率稍慢。相比于ICA-PCA故障監測模型，由于分布式ICA-PCA模型已確定引起故障的子塊，即建模矩陣和測試矩陣的維數大大降低，所以分布式 ICA-PCA模型的效率快于ICA-PCA模型。

2.5基于分布式ICA-PCA模型的故障診斷算法

綜合2.1節、2.2節、2.3節的分析，得到分布式ICA-PCA模型的故障診斷算法，其中，步驟（1）～（3）為離線建模階段，步驟（4）～（8）為在線監測階段，具體為：

（1）獲取正常數據，并進行歸一化處理，構成建模數據庫；

（2）對正常數據進行原始PCA分解，運用CPV準則提取 k個主成分，把過程數據劃分為k+1個子塊；

（3）對每個子塊首先進行獨立成分分析，獲取分離矩陣Wi，并對其殘差矩陣Ei進行PCA分解，獲取載荷矩陣Pi；

（4）對于新的樣本數據，同樣進行歸一化處理；

（5）計算每個子塊新的獨立成分矩陣 S?i和得分矩陣 ti；

（6）根據式（15）～式（21）計算每個子塊的I2、T2和SPE統計量及其對應的統計限；

（7）根據故障監測的結果，把子塊劃分為兩類：可監測到故障和無法監測到故障；

（8）利用式（25）求出引起該故障的變量，實現故障診斷。

3　TE過程仿真研究

為了說明所提出方法的性能，本節通過TE過程進行分布式 ICA-PCA、傳統 PCA、文獻[16]的ICA-PCA和文獻[22]的分布式 PCA的對比仿真實驗。

Tennessee Eastman（TE）仿真平臺是美國Eastman化學公司根據實際化工反應過程開發的，該平臺是一個開放的、具有挑戰性的化工模型仿真平臺[21,23]。整個過程包括以下5個主要單元：冷凝器、反應器、分離器、壓縮機和汽提塔。TE過程的流程如圖1所示。

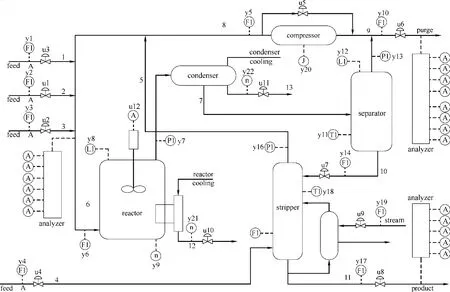
圖1　TE平臺流程Fig.1　TE benchmark process

TE過程包括12個操作變量和41個測量[21,23]，借鑒文獻[10,16]的分析，本文選擇了 33個變量，其中包括 11個操作變量，22個測量變量。采集過程平穩運行時的 960個數據作為訓練樣本，模擬故障工況時，采集 21種故障運行時的 960個樣本，故障均在樣本點161時引入。本文選用包含 960個樣本的正常和故障數據集，來源于網站http://depts.washington.edu/control/LARRY/TE/down load.html。

根據CPV準則，對原始數據選擇14個主成分進行傳統 PCA分解，建立 15個子塊的分布式ICA-PCA監測模型，通過檢測各個子塊的負熵值是否為零或接近零來選擇獨立成分數目，利用CPV準則確定子塊的主成分數目，所有統計限的置信度均為95%。15個子塊選擇的主成分數目和獨立成分數目如表1所示。

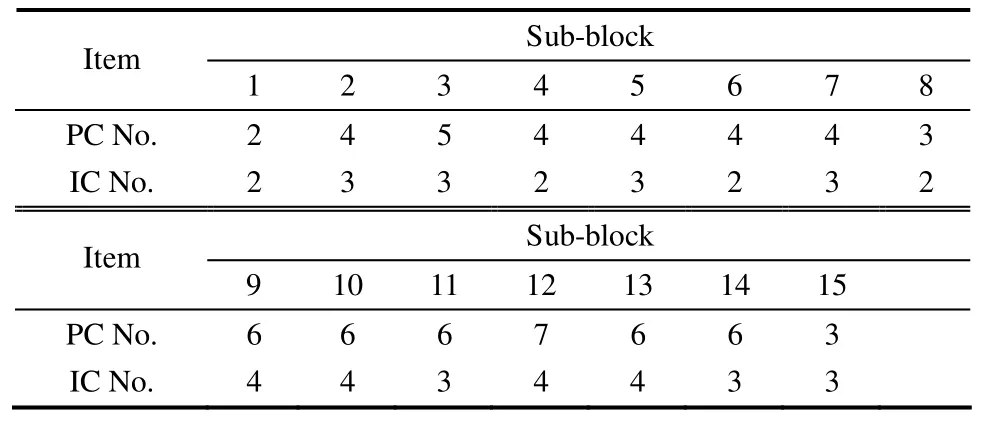
表1　子塊主成分和獨立成分數目Table 1　Selected PC and IC number in each sub-block

分別采用本文方法、傳統PCA方法、ICA-PCA方法、分布式PCA方法進行對比仿真實驗，其中，傳統PCA和ICA-PCA方法的數據來自于文獻[16]，分布式PCA方法的結果來源于文獻[22]。4種方法對于21種故障的漏報率如表2所示，黑體表示同一故障漏報率的最小值。由表2可知，本文的分布式ICA-PCA方法對 TE過程監測的改進效果是明顯的，即監測精度明顯提高，特別對于故障1～4，8～11，15～21，漏報率明顯低于另外3種方法。

引起故障5的原因是冷凝器冷卻水入口溫度階躍變化，在此模式下，從冷凝器到分離器的出口流量也會增加，導致分離器溫度和分離器冷卻水出口溫度升高。由于控制回路溫度補償的作用，約10 h后會再次達到穩態。文獻[16]中PCA模型的監測結果如圖2所示，從圖2可知： T2、SPE統計量能夠監測到第161～350樣本點的故障，但對于350樣本點之后的故障漏報率高，容易引起操作人員的誤判。實際上，在故障5模式下，350樣本點之后的壓縮機冷卻水的進口溫度依然高于其設定值[16]。

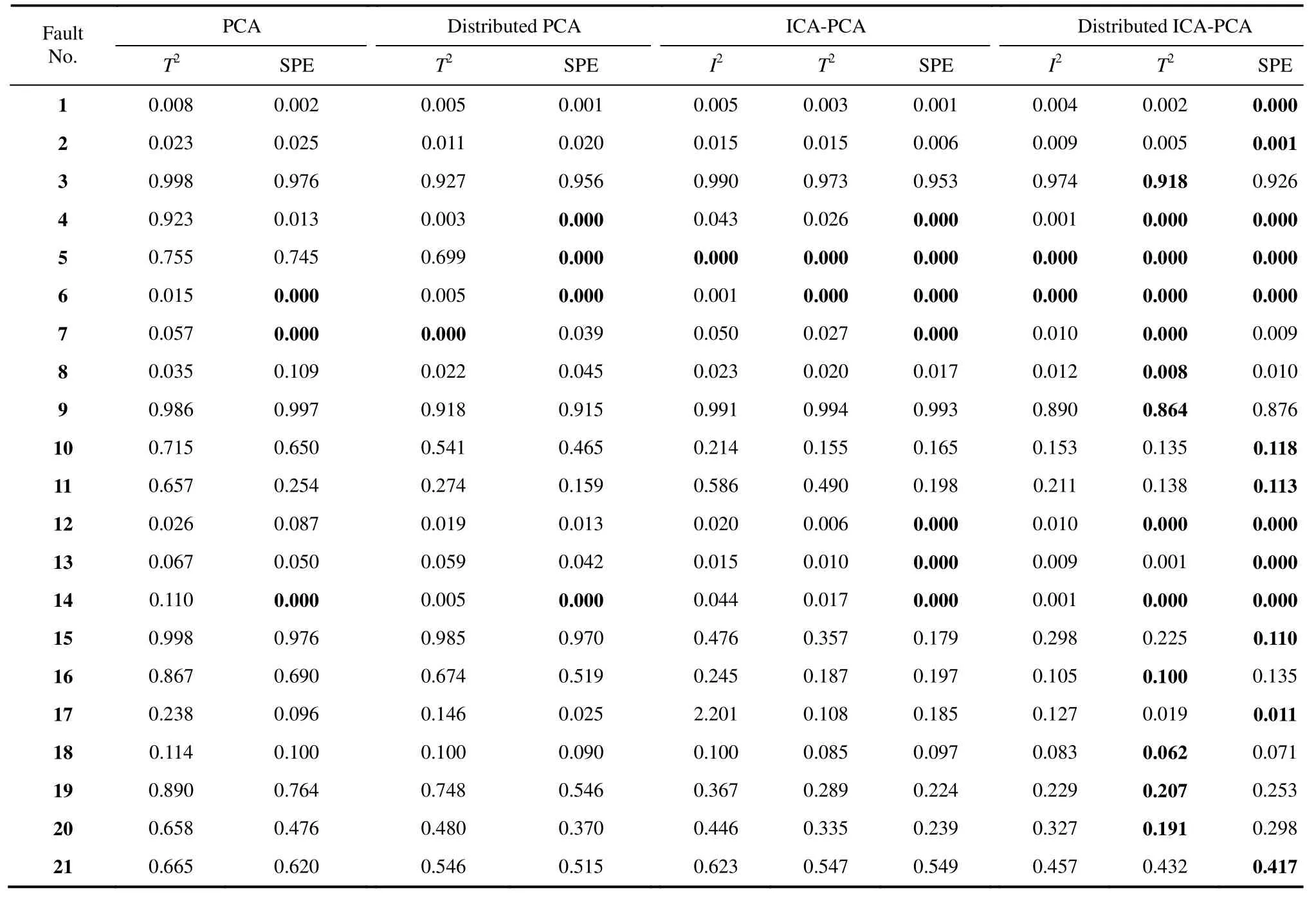
表2　TE過程中故障數據集的漏報率Table 2　Miss alarm rate of fault database in TE process

圖2　故障5的PCA監測結果Fig.2　Monitoring results of fault 5 by PCA

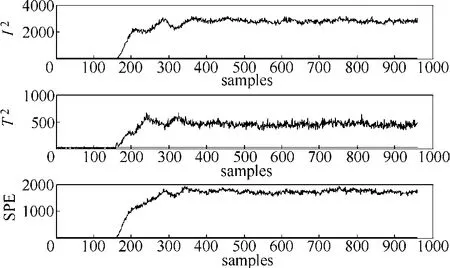
圖3　故障5的ICA-PCA監測結果Fig.3　Monitoring results of fault 5 by ICA-PCA

文獻[16]中ICA-PCA監測模型的結果如圖3所示，可以看出，其達到很好的監測效果，且從表 2可知， I2、T2和SPE統計量的漏報率均為零，但由于其建模的全局性，ICA-PCA模型對大型復雜工藝流程監測效果不理想，且不能實時診斷出引起故障的因素。在文獻[22]的分布式PCA監測模型中，對比各個子塊監測圖發現，只有子塊4和子塊6監測到故障。由圖4可知，子塊4和子塊6均包括變量15（解析塔液位）、變量17（汽提塔底部流量）、變量30（汽提塔液體產品流量）和變量33（冷凝器冷卻水流量），且其他子塊不包括這些變量。因此，變量15、變量17、變量30和變量33為引起故障5的主要原因。以子塊4和子塊6為研究對象，其分布式PCA監測結果如圖5所示，由圖5可知：分布式PCA監測模型子塊4、子塊6的SPE統計量在故障發生后一直處于報警狀態，但其 T2統計量在第350樣本點后不能監測到故障。圖6是本文的分布式ICA-PCA模型監測結果，從圖6可得：分布式ICA-PCA模型子塊4和子塊6的I2、T2和SPE 3個統計量在故障發生后均處于報警狀態，3個統計量的幅值大，結合表2可知，3個統計量平均漏報率均為零。

表3列出了4種方法對故障5和故障10的監測時間，結合表2故障5的漏報率說明：對于故障5，分布式ICA-PCA監測模型與ICA-PCA監測模型相比，其在精確監測到故障的同時，并沒有犧牲系統的監測效率；與分布式PCA模型和PCA模型相比，雖然監測效率稍慢，但漏報率明顯降低。

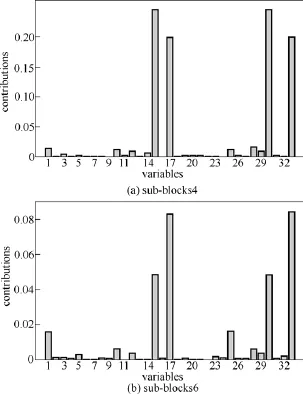
圖4　兩個子塊的變量貢獻圖Fig.4　Variable contributions in two sub-blocks

圖5　故障5的分布式PCA監測結果Fig.5　Monitoring results of fault 5 by distributed PCA

圖6　故障5的分布式ICA-PCA監測結果Fig.6　Monitoring results of fault 5 by distributed ICA-PCA

表3　故障5的監測時間Table 3　Monitoring time of fault 5/s

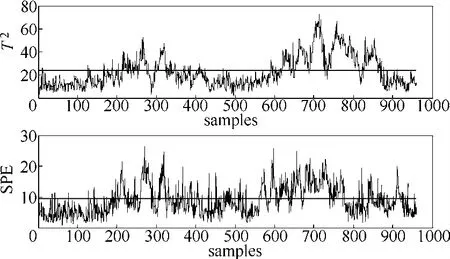
圖7　故障10的PCA監測結果Fig.7　Monitoring results of fault 10 by PCA

引起故障10的原因是物料C的溫度發生隨機變化，文獻[22]中PCA模型的監測結果如圖7所示，根據表2，PCA模型對于故障10的故障漏報率高。圖8為文獻[16]的ICA-PCA模型監測結果，相比于圖7，ICA-PCA模型提高了監測性能。由表2可知，ICA-PCA方法與PCA相比漏報率更低，但由于其建模的局限性，仍存在一定的漏報。在文獻[22]分布式PCA監測模型中，對比15個子塊的監測效果發現，僅子塊1、子塊2和子塊15能夠很好地監測故障。分析圖9子塊1、子塊2和子塊15的變量貢獻圖，3個子塊均包括變量18（汽提塔溫度）、變量19（汽提塔上部蒸汽流量）和變量27（壓縮機再循環閥），且其他子塊不包含這3個變量，因此，變量18、19和27是引起故障10的主要原因。圖10是子塊1、子塊2和子塊15的分布式PCA監測圖。分布式ICA-PCA模型對于故障10的監測結果如圖11所示，與圖10、圖8和圖7相比，圖11提高了監測性能。根據表2中4種方法對于故障10的漏報率可知，分布式ICA-PCA模型3個統計量的漏報率的均值小（最小值為0.118），說明相較于其他3種方法，本文方法對于故障10的監測精確性更高。

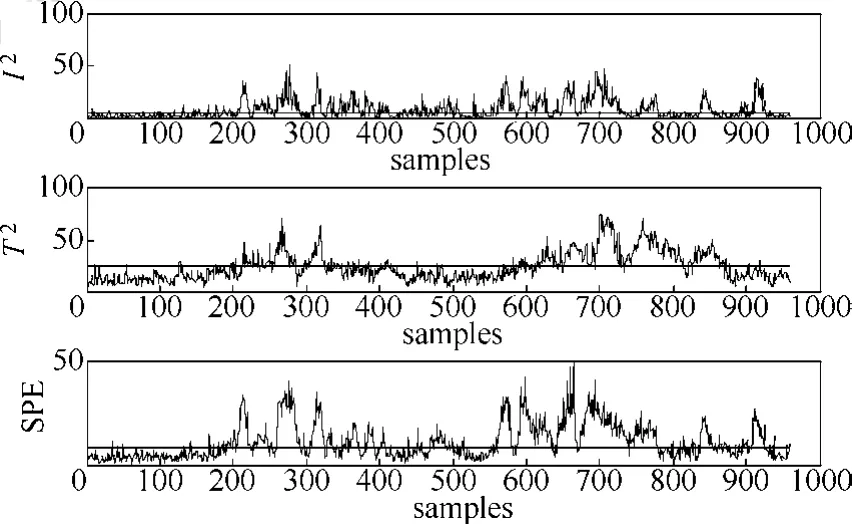
圖8　故障10的ICA-PCA監測結果Fig.8　Monitoring results of fault 10 by ICA-PCA

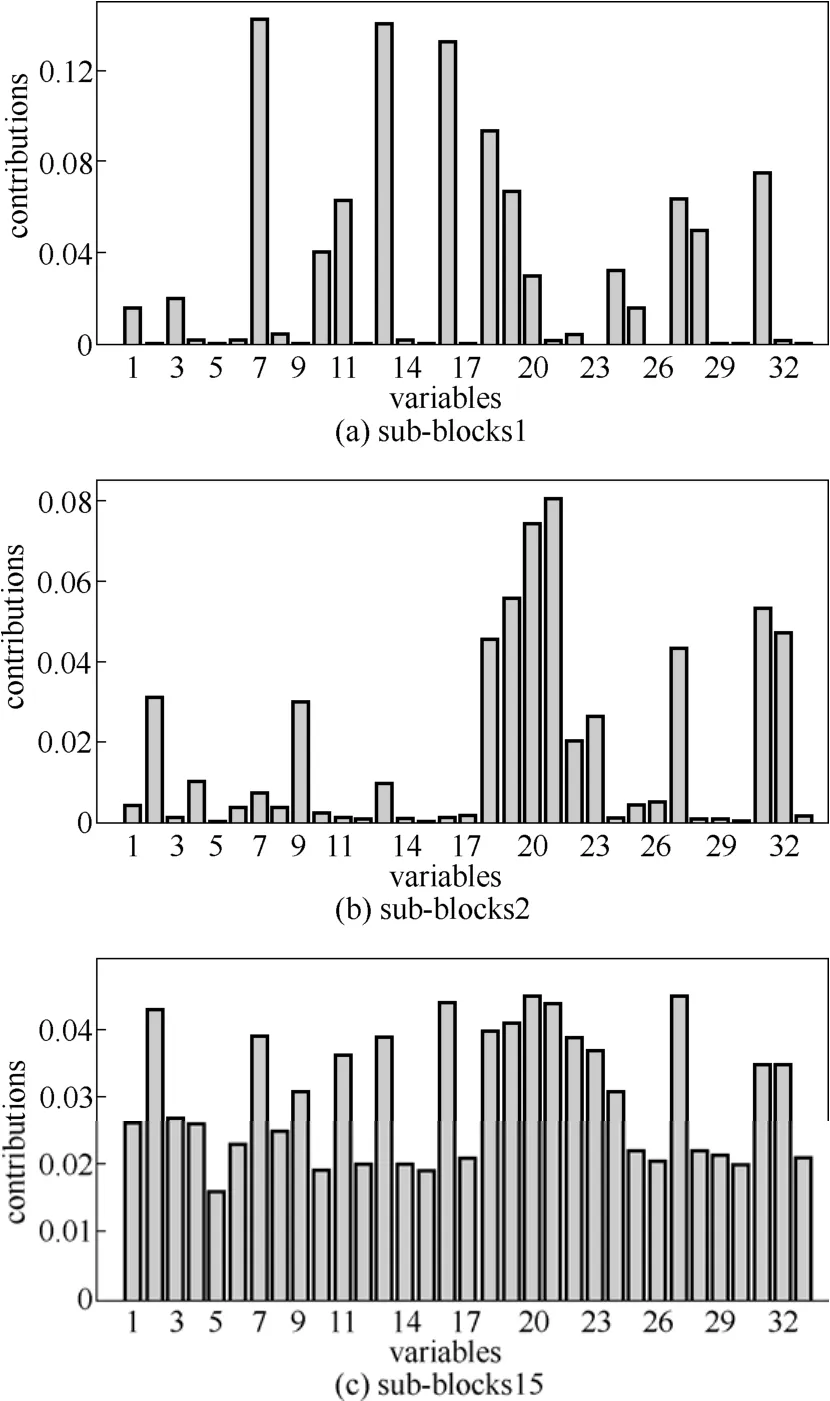
圖9　3個子塊的變量貢獻圖Fig.9　Variable contributions in three sub-blocks

圖10　故障10的分布式PCA監測結果Fig.10　Monitoring results of fault 10 by distributed PCA

表4　故障10的監測時間Table 4　Monitoring time of fault 10/s

表4給出了故障10的監測時間，根據表2 中4種監測模型對故障10的漏報率可以得出：分布式ICA-PCA監測模型與ICA-PCA監測模型相比，不僅提高了監測精度，而且提高了監測效率；與分布式PCA模型和PCA模型相比，雖然降低了漏報率，但監測效率也稍低。

考慮每種方法分別對 21種故障監測效率的相似性，結合對表3和表4的分析可知：本文所提方法與PCA方法和分布式PCA方法相比，監測效率稍低；與ICA-PCA模型相比，提高了監測效率。

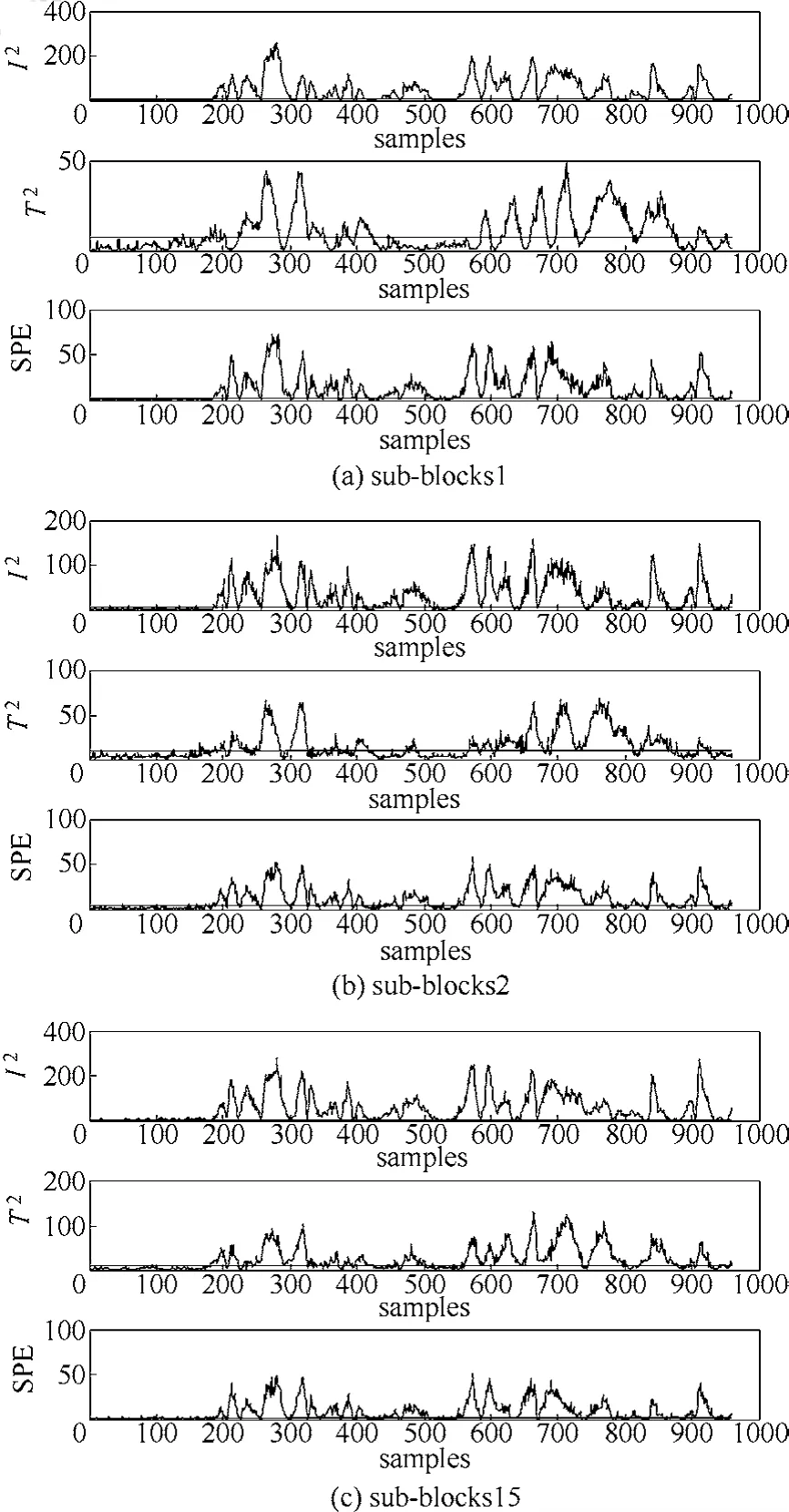
圖11　故障10的分布式ICA-PCA監測結果Fig.11　Monitoring results of fault 10 by distributed ICA-PCA

4　結　論

本文提出了一種基于分布式 ICA-PCA模型的工業過程故障監測方法，針對復雜工業過程難以自動劃分子塊和過程數據的非高斯性，該方法首先通過原始 PCA分解把工業過程自動劃分為互不相關的子塊，其次對各個子塊采用 ICA-PCA的兩步信息提取策略，分別提取出子塊數據中的高斯信息和非高斯信息，最后構建各子塊的 I2、T2和SPE 3個統計量及對應的統計限，并通過變量貢獻圖確定故障變量，實現故障監測和診斷。TE平臺的仿真結果表明所提出方法的性能：該方法適用于復雜工業過程自動劃分子塊和過程數據存在非高斯信息的情況。

References

[1]Nomikos P, MacGregor J F. Monitoring batch processes using multiway principal component analysis [J]. AIChE J., 1994, 40: 1361-1375.

[2]Nomikos P, MacGregor J F. Multi-way partial least square in monitoring batch processes [J]. Chem. Intell. Lab. Syst., 1995, 30: 97-108.

[3]Ku W, Storer R H, Georgakis C. Disturbance detection and isolation by dynamic principal component analysis [J]. Chem. Intell. Lab. Syst., 1995, 30: 179-196.

[4]Bakshi B R. Multiscale PCA with applications to multivariate statistical process monitoring [J]. AIChE J., 1998, 44: 1596-1610.

[5]Cheng C, Chiu M S. Nonlinear process monitoring using JITL-PCA [J]. Chem. Intell. Lab. Syst., 2005, 76:1-13.

[6]Kim D, Lee I B. Process monitoring based on probabilistic PCA [J]. Chemom. Intell. Lab. Syst., 2003, 67: 109-123.

[7]Zhao Zhonggai (趙忠蓋), Liu Fei (劉飛). Factor analysis and its application to process monitoring [J]. Journal of Chemical Industry and Engineering (China) (化工學報), 2007, 58 (4): 970-974.

[8]Zhang Y, Ma C. Fault diagnosis of nonlinear processes using multiscale KPCA and multiscale KPLS [J]. Chem. Eng. Sci., 2011, 66: 64-72.

[9]Song Bing (宋冰), Ma Yuxin (馬玉鑫), Fang Yongfeng (方永鋒), Shi Hongbo (侍洪波). Fault detection for chemical process based on LSNPE method [J]. CIESC Journal (化工學報), 2014, 65 (2): 620-627.

[10]Lee J M, Yoo C K, Lee I B. Statistical process monitoring with independent component analysis [J]. J. Process Control., 2004, 14: 467-485.

[11]Chen Guojin (陳國金), Liang Jun (梁軍), Qian Jixin (錢積新). ICA and its application to chemical process monitoring and fault diagnosis [J]. Journal of Chemical Industry and Engineering (China) (化工學報), 2003, 54 (10): 1474-1477.

[12]Lee J M, Yoo C K, Lee I B. Statistical monitoring of dynamic processes based on dynamic independent component analysis [J]. Chem. Eng. Sci., 2004, 59: 2995-3006.

[13]Yoo Chang Kyoo, Lee Dae Sung. Application of multiway ICA for on-line process monitoring of a sequencing batch reactor [J]. Water Research, 2004, 4: 1715-1732.

[14]Ge Z Q, Song Z H. Performance-driven ensemble learning ICA model for improved non-Gaussian process monitoring [J]. Chemometrics and Intelligent Laboratory Systems, 2013, 123: 1-8.

[15]Kano M, Hasebe S, Hashimoto I, Ohno H. Evolution of multivariate statistical process control: application of independent component analysis and external analysis [J]. Comput. Chem. Eng., 2004, 28: 1157-1166.

[16]Ge Z Q, Song Z H. Process monitoring based on independent component analysis-principal component analysis (ICA-PCA) and similarity factors [J]. Ind. Eng. Chem. Res., 2007, 46: 2054-2063.

[17]MacGregor J F, Jaeckle C, Kiparissides C, Kourtoudi M. Process monitoring and diagnosis by multiblock PLS methods [J]. AIChE J., 1994, 40: 826-838.

[18]Westerhuis J A, Kourti T, MacGregor J F. Analysis of multiblock and hierarchical PCA and PLS models [J]. J. Chemom., 1998, 12: 301-321.

[19]Cherry G A, Qin S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis [J]. IEEE Trans. Semiconductor Manufacturing, 2006, 19: 159-172.

[20]Ge Z Q, Song Z H. Two-level multiblock statistical monitoring for plant-wide processes [J]. Korean J. Chem. Eng., 2009, 26, 1467-1475.

[21]Ge Z Q, Song Z H. Nonlinear soft sensor development based on relevance vector machine [J]. Ind. Eng. Chem. Res., 2010, 49: 8685-8693.

[22]Ge Z Q, Song Z H. Distributed PCA model for plant-wide process monitoring [J]. Ind. Eng. Chem. Res., 2013, 52: 1947-1957.

[23]Downs J, Vogel E F. A plant-wide industrial process control problem [J]. Computers &Chemical Engineering, 1993, 17: 245-253.

Fault monitoring of industrial process based on distributed ICA-PCA model

ZHONG Lusheng, HE Dong, GONG Jinhong, ZHANG Yongxian
(College of Electrical Engineering, East China Jiaotong University, Nanchang 330013, Jiangxi, China)

A fault monitoring method based on distributed independent component analysis-principal component analysis (ICA-PCA) model is proposed, which is suitable for complex industrial process that cannot be divided into several sub-blocks through an automatic way and has non-Gaussian information. Firstly, an initial PCA decomposition is carried out upon the variables of the whole process. By constructing sub-blocks through different directions of PCA principal components, the original feature space can be automatically divided into several sub-feature spaces. In addition, a two step extractions of the ICA-PCA information are carried on upon all sub-blocks in order to extract both Gaussian and non-Gaussian information, establishing the new statistics and their statistic limits. Finally, the simulation of TE process shows that the proposed fault detection model is efficient and feasible.

complex industrial process; automatic partitioning sub-blocks; non-Gaussian; ICA-PCA; fault monitoring

引　言

隨著工業過程生產規模的不斷擴大，對其過程的故障監測已成為過程控制領域的研究熱點。其中，主成分分析（PCA）和偏最小二乘法（PLS）在過程監測和故障診斷領域得到了成功的應用。之后研究人員又提出PCA、PLS的拓展方法，并成功應用在故障監測中：Nomikos等[1-2]提出使用多向 PCA 和PLS監測批處理過程；Ku等[3]使用動態PCA實現了故障的監測和分離；Bakshi[4]提出使用基于小波分析的多尺度PCA監測不同頻率范圍的故障。最近，國內外學者又提出一些新的方法用于工業過程故障監測。Cheng等[5]提出使用實時學習（JITL）和 PCA結合的方法監測非線性靜態或動態系統；Kim等[6]指出：針對過程數據存在噪聲情況，使用概率主成分分析（PPCA）構建 PPCA故障監測模型；趙忠蓋等[7]針對PCA需要噪聲各向同性的限制，提出基于因子分析的故障監測模型；Zhang等[8]將核函數的思想引入到多尺度主元分析中，不僅改善了常規PCA在時頻域的局部分析能力，而且使其能夠處理非線性過程。這些方法通常要求過程數據服從高斯分布[9]，這一條件在復雜的工業過程中卻很難滿足。

date: 2015-05-04.

ZHONG Lusheng, lszhongzju@163.com

supported by the National Natural Science Foundation of China (61263010, 60904049), the Natural Science Foundation of Jiangxi Province (20114BAB211014) and the Project of Education Department of Jiangxi Province (GJJ14399).

10.11949/j.issn.0438-1157.20150546

TP 277

A

0438—1157（2015）11—4546—09

2015-05-04收到初稿，2015-08-06收到修改稿。

聯系人及第一作者：衷路生（1979—），男，博士，副教授。

國家自然科學基金項目（61263010，60904049）；江西省自然科學基金項目（20114BAB211014）；江西省教育廳項目（GJJ14399）。