探尋本質 多題歸一
2015-09-10 09:07:07孫飛
初中生世界·七年級 2015年2期
孫飛
數學學習離不開解題.在解決問題時,我們可對問題的局部(條件或結論)進行改變(往往是位置或數量),從而得到新的數學問題.通過這樣的改變,我們能夠實現多題歸一的目的,從而提升解決問題的能力.下以一例予以說明.
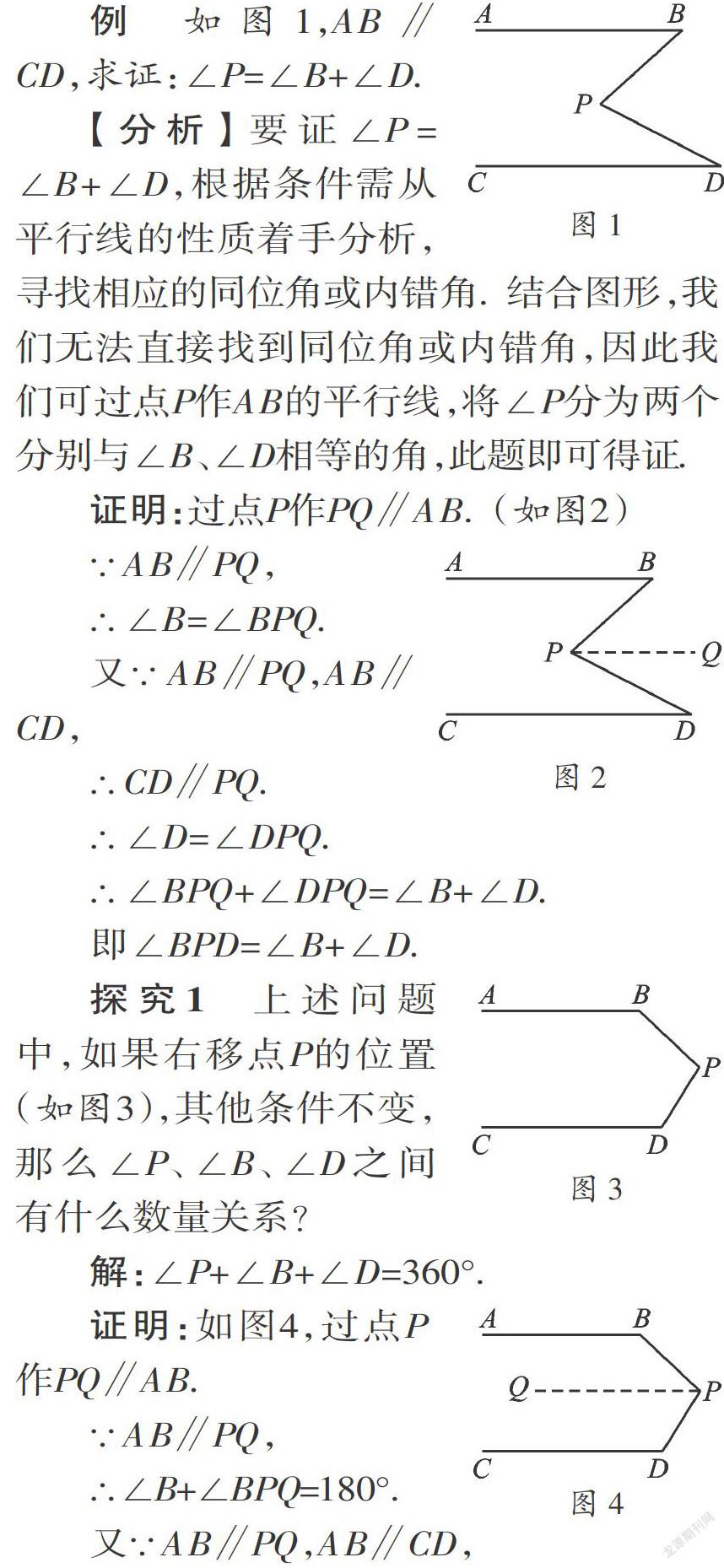
【分析】要證∠P=∠B+∠D,根據條件需從平行線的性質著手分析,尋找相應的同位角或內錯角.結合圖形我們無法直接找到同位角或內錯角,因此我們可從點P作AB的平行線,將∠P分為兩個分別與∠B、∠D相等的角,此題即可得證.
【分析】根據上述例子的解題方法,利用平行線的性質,不難推理出∠P=∠D-∠B,根據兩直線平行,同位角相等;三角形外角的性質即可證之.
探究3 如果繼續改變點P的位置(如圖6),其它條件不變,那么∠P、∠B、∠D之間又有什么數量關系?
【分析】本題中沒有已知的同位角(或內錯角)可以利用,我們可根據上面積累的解題經驗,作出合適的輔助線,構造出同位角(或內錯角),從而解決問題.

探究4 如果將點P移到直線CD的下方,(如圖8、圖9),其它條件不變,那么∠P、∠B、∠D之間又有什么數量關系?
【分析】根據圖8、圖9,由上述的探究思路,不難得出以下結論.
如圖8,有∠P=∠B-∠D.
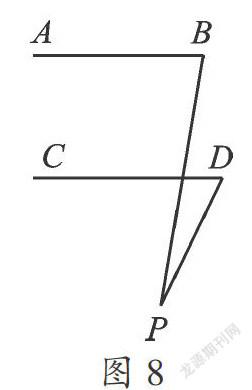
證明過程參見圖5.
如圖9,有∠P=∠D-∠B.
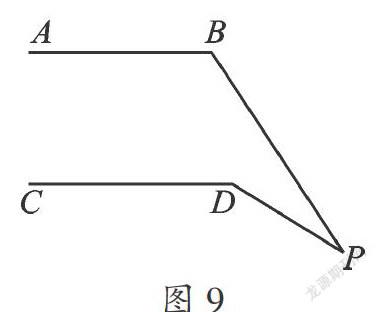
證明過程參見圖6.
改變問題的局部只是給問題“換了件外衣”,其本質是并未改變.在平時的數學學習中,我們要善于在“變”中找出“不變”,洞察本質,從而實現問題的關聯.
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
小學生學習指導(中年級)(2022年4期)2022-04-26 06:34:46
今日農業(2021年9期)2021-11-26 07:41:24
中學生數理化·七年級數學人教版(2021年10期)2021-11-22 07:53:00
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
中等數學(2021年11期)2021-02-12 05:11:46
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42

