握手的次數(shù)

范敏祎

我們經(jīng)常會碰到有關(guān)求多邊形對角線條數(shù)的問題，那么這樣的問題該怎么去解決，如何去思考呢？

首先我們可以通過畫圖來找到關(guān)于多邊形對角線的規(guī)律

例如： 四邊形對角線有2條 五邊形對角線有5條.

可以看到，2，5，9，14……這些數(shù)字背后存在著規(guī)律，我們可以根據(jù)這些規(guī)律去解決問題.那么，有沒有簡單一點的方法呢？我們可以從多邊形對角線的定義來想：連接多邊形不相鄰的兩個頂點的線段，叫做多邊形的對角線.

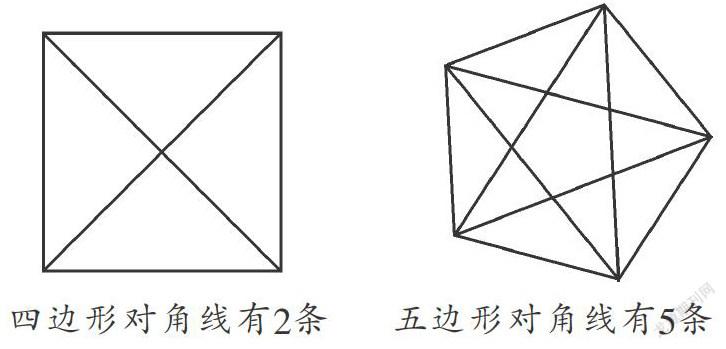
先考慮從一個頂點發(fā)出的對角線數(shù)目，它不能向本身引對角線，不能向相鄰的兩個頂點引對角線，它只能向n邊形剩下的（n-3）個頂點連接對角線.因此，一個n邊形從一個頂點能引的對角線數(shù)為n-3條；又因為n邊形共有n個頂點，就一共能引n（n-3）條，但是考慮到每一條對角線都是由兩個頂點連接構(gòu)成的，這樣計算所得的對角線中有一半是重復(fù)的，所以正確答案應(yīng)該是 .

而多邊形對角線的問題與另一個著名的問題有著異曲同工之妙，那就是“握手問題”.

“握手問題” 屋子里有n個人，每兩個人都要握一次手，又不能重復(fù)握手，那么這n個人一共握了幾次手？

我們可以把每個人看做多邊形的頂點，每兩個人握一次手就是每兩個頂點之間連接一條線段.因不能和自己握手，所以一個人可以和n-1個人握手，所以總握手次數(shù)就是n（n-1）次；但你和我握與我和你握的意義是一樣的，所以總次數(shù)中有一半是重復(fù)的，所以正確答案是 .

大家可以發(fā)現(xiàn)：多邊形對角線問題與握手問題的本質(zhì)是相同的.多邊形對角線條數(shù)的解決其實是“握手問題”的一種應(yīng)用.

握手問題除了能解決多邊形條數(shù)問題外，還能解決送禮物問題：n個人，每兩個人之間都要互送禮物一共要準(zhǔn)備多少份禮物？握手問題中，我和你握手，你和我握手，屬于重復(fù)，具有相同的意義；

送禮物問題中，我送你禮物，你送我禮物具有不同意義，不屬于重復(fù)，所以可以得到n個人互相送禮物要送n（n-1）份.

類似，車票問題：一條剛開通的鐵路上一共建設(shè)有x個車站，每兩個車站之間要準(zhǔn)備車票，那么要準(zhǔn)備多少種車票？這個問題和送禮物問題同理，甲車站到乙車站的車票與乙車站到甲車站的車票意義不同，所以這條鐵路x個車站之間一共要準(zhǔn)備x（x-1）種車票.

看到這，大家有沒有感受到數(shù)學(xué)問題很多都是相通的，關(guān)鍵就是識破它們各自的“偽裝”.如果我們以后遇到一個較復(fù)雜的問題，我們可以試著像解決握手問題一樣，先把它轉(zhuǎn)換成一個我們所熟悉的問題，然后去探索兩者之間的關(guān)系，這樣去思考問題，復(fù)雜的數(shù)學(xué)問題有時候就不是一個難題了.

（指導(dǎo)老師：浦長宇）