結構參數對泵站卸荷閥影響的仿真及分析

徐 鵬

（北京天地瑪珂電液控制系統有限公司，北京 100013）

0 引言

卸荷閥礦山泵站系統的關鍵部件之一，是實現泵站壓力自動調節功能的重要壓力控制元件[1]，其功能是在泵持續運轉的情況下滿足綜采工作面斷續用液的需求[2]，其性能的好壞對其自身可靠性以及泵站系統能否穩定運行有著直接影響[3]，進而影響乳化液泵站的供液質量和系統的節能效果[4]。

本文針對某型號的泵站卸荷閥，深入分析其工作原理，建立數學模型并確定關鍵結構參數，利用計算機仿真技術，分析關鍵結構參數對卸荷閥不同性能指標的影響及其規律，并根據仿真結果優化結構設計。

1 泵站卸荷閥的工作原理

某型號的泵站卸荷閥的結構如圖1所示，其主要結構分為單向閥、主閥、先導調壓閥三部分，其中單向閥出口通往工作面液壓系統，主閥出口通回液箱。由于礦山泵站系統工作介質為高水基乳化液，針對高水基介質易泄漏、磨損、易生銹等問題，泵站卸荷閥采用直接密封結構、耐磨材料配對等相應措施[5]，先導調壓閥直接選用硬度高、耐腐蝕性好的陶瓷球作為閥芯[6]。

圖1 泵站卸荷閥結構圖

其工作原理如圖2所示，泵出口液體分為四路，一路通過單向閥進入工作面液壓系統，一路通過單向閥進入控制活塞腔，一路通過主閥阻尼孔以及主閥配合間隙進入彈簧腔，一路通過主閥卸荷流回液箱[2]。卸荷閥的開啟由先導調壓閥控制，當負載端壓力大于先導調壓閥設定壓力時，先導調壓閥開啟，彈簧腔內液體流回液箱，隨著先導調壓閥開口量增大，流經主閥阻尼孔的壓力損失增大，達到主閥開啟壓差，主閥開啟，單向閥關閉，負載端壓力通過控制活塞作用于先導調壓閥維持其開啟，乳化液泵通過主閥卸載。當負載端壓力低于先導調壓閥設定壓力時，先導閥復位關閉，主閥關閉，單向閥重新開啟，泵站繼續向工作面供液[7]。

圖2 泵站卸荷閥工作原理圖

2 泵站卸荷閥的數學模型建立與分析

衡量卸荷閥性能好壞的指標為至工作面出口處的壓力變化特性，即卸載閥的主閥升壓與卸荷時該處允許的壓力變化范圍與所需時間[4]，即動態特性。影響卸荷閥動態特性的因素很復雜，除閥自身結構參數之外，還受到系統中管路及其他零件影響，在本研究中忽略其他零件動態特性影響以及過液孔的液阻、閥芯自重與液壓卡緊力的影響，假定閥出口壓力為零，以主閥芯、先導閥芯與控制活塞為研究對象，建立如下數學模型：

1）主閥芯運動微分方程：

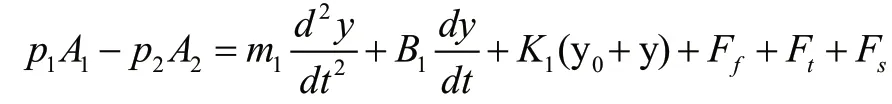
式中：Fs為作用在主閥上的穩態液動力：

Ft為作用在主閥上的瞬態液動力：

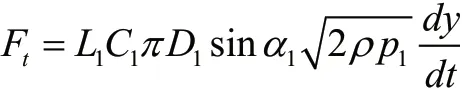
Ff為主閥芯與閥套間的摩擦力。

2）通過主閥口的流量方程：

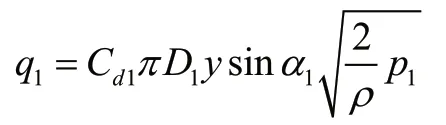
3）主閥芯阻尼孔節流方程[8]：

4）先導閥芯運動微分方程：

式中：Fs2為作用在先導閥上的穩態液動力：

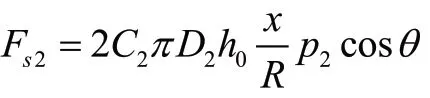
Ft2為作用在先導閥上的瞬態液動力：

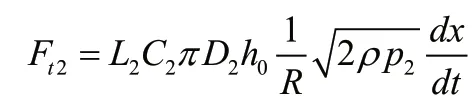
5）先導閥口流量方程：

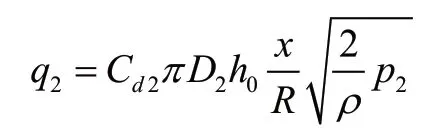
總流量方程：

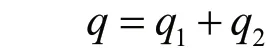
7）控制腔流量連續性方程[9]：

8）控制活塞運動微分方程：

9）先導閥開啟瞬間，x=y=0，q2＞0，有：

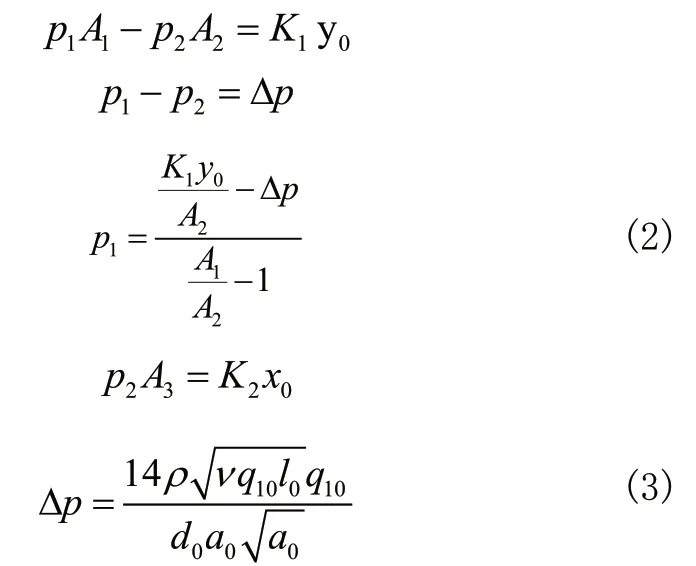
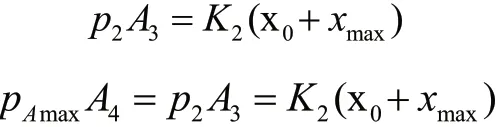
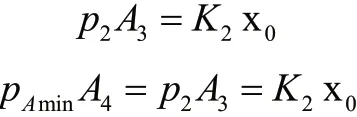
12）系統壓力波動范圍：

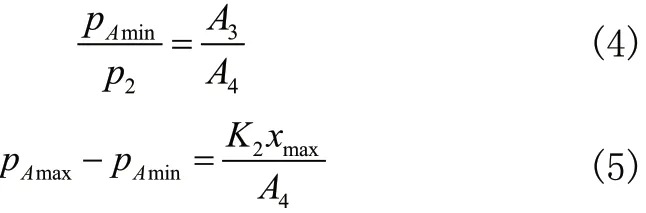
由式(1)知，壓力p2的響應速度主要由主閥芯控制腔體積V0決定。

由式(2)與式(3)可知，p2由p1和pΔ決定，其關鍵因素的參數為K1y0、A1、A2、d0、l0值，但對p1的影響，K1y0遠不如A1/A2大，對pΔ的影響，l0與d0起關鍵因素。

由式(4)知，系統壓力下限pAmin則由先導閥口與控制活塞的面積比A3/A4和主閥芯上腔壓力p2決定。

由式(5)知，先導閥調壓彈簧剛度K2越大，調節靈敏度越大，x稍有變化便會導致壓力波動范圍增大。

綜上所述，對泵站卸荷閥性能起關鍵作用的結構參數為阻尼孔參數l0與d0，主閥芯控制腔體積V0、先導閥口與控制活塞的面積比A3/A4、先導閥調壓彈簧剛度K2和主閥芯上下腔面積比A1/A2，下面分別對其各自影響進行仿真分析。

以上公式中：

p2、p1為主閥芯上下腔的液壓力（Pa）；

pA為單向閥出口壓力（Pa）；

A2、A1為主閥芯上下腔的作用面積（m2）；

A3、A4為先導閥、控制活塞作用面積（m2）；

K1、K2為主閥、先導閥的彈簧剛度（N/m）；

y0、x0為主閥、先導閥的彈簧預壓縮量（m）；

x、y、z為先導閥、主閥、控制活塞的位移（m）；

m1、m2、m3為先導閥、主閥、控制活塞的質量（m）；

C1、C2為主閥、先導閥閥口的流量系數；

D1、D2為主閥、先導閥出流口直徑（m）；

α1為主閥芯閥口半錐角；

θ為先導閥座半錐角；

R為先導球閥半徑（m）；

a0為阻尼孔有效作用面積（m2）；

d0為阻尼孔直徑（m）；

l0為阻尼孔長度（m）；

ρ為液體密度（kg/m3）；

v為液體運動粘度（m2/s）；

K為液體彈性模量（MPa）；

V0為主閥芯控制腔體積（m3）。

3 Runge-Kutta算法

針對各微分方程，使用Runge-Kutta[10,11]對其進行迭代求解，該方法是一種在工程上應用廣泛的求解處置問題的高精度單步算法。

假設初值問題：

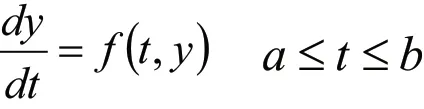
該問題的解y(t)及f(t,y)足夠光滑。將y(ti+1)在ti處做n階泰勒展開，得將，得：

當h充分小時，

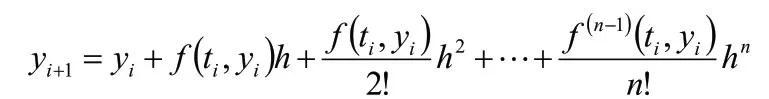
以上為n階泰勒法。如果在積分區間[ti+tI+1]內，多預估幾個點的斜率值，并用加權平均數作為平均斜率的近似值，經過數學推導、求解，可以得到四階Runge-Kutta公式，也就是在工程中應用廣泛的經典Runge-Kutta算法。

應用Fortran語言編寫計算程序，采用Runge-Kutta算法求解描述卸荷閥模型的微分方程組，算法如圖3所示，從而建立了泵站卸荷閥動態仿真分析模型，該模型能夠計算泵站卸荷閥各口壓力、流量和閥芯位移隨時間變化規律。

圖3 泵站卸荷閥動態分析算法

4 仿真結果與分析

在本研究中，我們初設單步計算時間為0.1s，計算步數為100，總計10s；計算初始變量設置為x=y=z=0mm，dx/dt=dy/dt=dz/dt=0，P1=P2=1bar。

模型主要結構參數如表1所示。

表1 模型主要結構參數

1）阻尼孔長度8mm不變，分別設定阻尼孔徑為0.5mm、1mm與3mm，進行批處理運算，獲得系統壓力曲線如圖4所示。

圖4 不同阻尼孔徑下系統壓力圖

由圖4可看出，阻尼孔長徑比越小，系統壓力波動越小，響應越快，但當長徑比小于某極限值時，系統壓力波動為零，此時卸荷閥的工作狀態為溢流，導致回液管路液體溫度急劇升高，對系統不利應予避免。孔徑過小，還會容易造成阻尼孔堵塞，使得卸荷閥失效。在實際設計中，應合理選取阻尼孔長徑比，該參數值過大或過小均對卸荷閥性能產生不利影響。

2）主閥芯直徑不變，分別設定主閥芯控制腔長度為22mm、44mm與88mm，進行批處理運算，獲得系統壓力曲線如圖5所示。

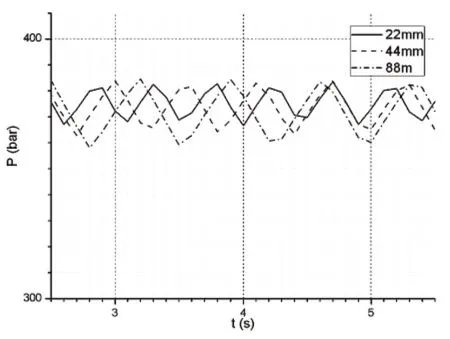
圖5 不同控制腔體積下系統壓力圖

由圖5可以看出，控制腔長度越小，即體積越小，系統壓力響應越快，壓力波動越小，在保證主閥芯開度滿足閥口阻力損失要求的情況下，應盡量減小彈簧腔的長度，使卸荷閥獲得更好的動態特性。

3）先導閥座孔直徑5mm不變，分別設定控制活塞直徑為5.1mm、5.3mm與6mm，進行批處理運算，獲得系統壓力曲線如圖6所示。

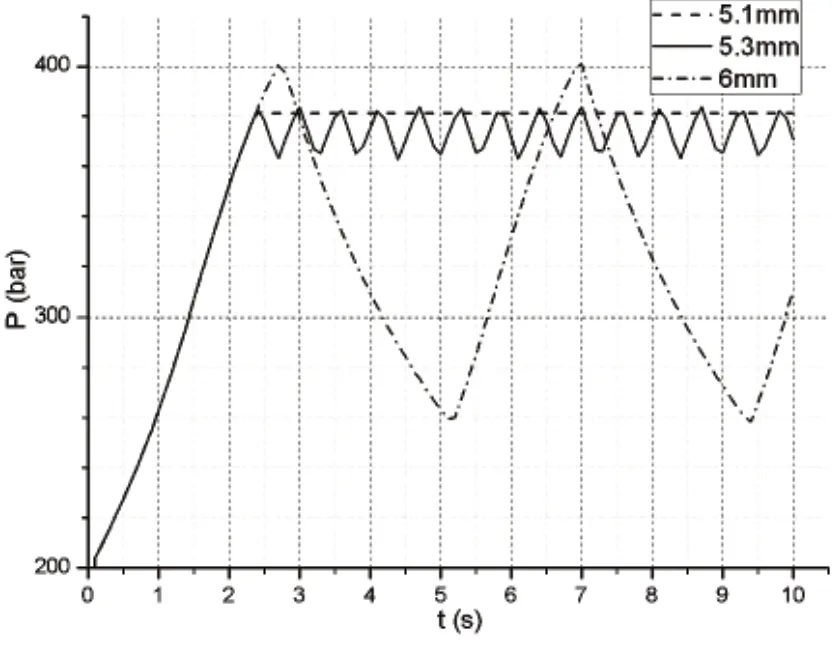
圖6 不同先導閥口與控制活塞面積比下系統壓力圖

由圖6可以看出，先導閥口與控制活塞面積比越小，系統壓力波動越小，響應越快，但當兩者面積比接近于1時，系統壓力波動為零，此時卸荷閥工作狀態為溢流，應予避免。在實際設計中，應合理選取先導閥口與控制活塞面積比，該參數值過大或過小均對卸荷閥性能產生不利影響。

4）分別設定調壓彈簧剛度為100N/mm、200N/mm與400N/mm，進行批處理運算，獲得系統壓力曲線如圖7所示。

由圖7可以看出，調壓彈簧剛度越小，系統壓力響應越快，壓力波動越小，在保證調壓彈簧預壓縮力滿足額定開啟壓力的情況下，應盡量減小調壓彈簧剛度，從而使卸荷閥獲得更好的動態特性。

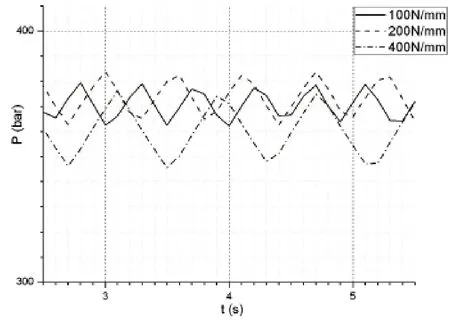
圖7 不同調壓彈簧剛度下系統壓力圖

5）主閥座孔直徑（即主閥芯下腔直徑）為46mm，分別設定主閥芯上腔直徑為46.5mm、50mm與80mm，進行批處理運算，獲得系統壓力曲線如圖8所示。其中主閥上腔直徑80mm時閥芯位移曲線如圖9所示。

圖8 不同主閥上下腔面積比下系統壓力圖

圖9 上腔直徑80mm時主閥芯位移圖

由圖8可以看出，在主閥上下腔面積比越大，系統壓力波動越小，響應越快。當兩者面積比超過極限值時，盡管系統壓力波動在1MPa之內，但由圖9可以看出，此時主閥芯在一定開度下震蕩，不能實現正常開關，工作狀態為溢流，應予避免。在實際設計中，應合理選取主閥芯上下腔面積比，該參數值過大或過小均對卸荷閥性能產生不利影響。

5 結束語

1）主閥芯阻尼孔長徑比、主閥芯控制腔體積、先導閥口與控制活塞面積比、調壓彈簧剛度、主閥芯上下腔面積比是影響泵站卸荷閥性能的5個關鍵結構參數。

2）減小主閥芯控制腔體積與調壓彈簧剛度有利于提高泵站卸荷閥的動態響應。

3）主閥芯阻尼孔長徑比、先導閥口與控制活塞面積比與主閥芯上下腔面積比的選取需適中，過大或過小均對系統不利。

4）在未來進一步的研究中，需通過試驗與仿真相結合的方式對這5個參數的匹配關系進行分析，用以優化泵站卸荷閥的設計，提高產品性能。

[1] 韓建華,劉志奇.基于遺傳算法的卸載閥結構參數優化[J].太原科技大學學報,2011,(08)：305-308.

[2] 王國法,等.液壓支架控制技術[M].北京：煤炭工業出版社,2010：19-24.

[3] 王偉.泵站溢流閥模型的動態特性仿真及分析[J].制造業自動化,2014,(08)：100-102,106.

[4] 袁利才.一種新型礦用卸載閥的研究[J].液壓氣動與密封, 2011,(09)：46-49.

[5] 弓永軍,周華,楊華勇.結構參數對先導式純水溢流閥性能的影響[J].浙江大學學報(工學版),2006,(05)：869-873.

[6] 賀小峰,黃國勤,楊有勝,李壯云.球閥閥口流量特性的試驗研究[J].機械工程學報,2008,(08)：30-33.

[7] 李培良.電磁卸荷閥動態特性仿真及流場數值模擬[D].太原：太原理工大學,2012：11-13.

[8] 宋鴻堯,等.液壓閥設計與計算[M].北京：機械工業出版社,1982：100-102,124-127.

[9] 蔡亦剛.流體傳輸管道動力學[M].浙江：浙江大學出版社,1990：6-8.

[10] 富明慧,梁華力.一種改進的精細龍格-庫塔法[J].中山大學學報,2009,48(5)：1-5.

[11] 李夏云,陳傳淼.用龍格-庫塔法求解非線性方程組[J].數學理論與應用,2008,28(2)：62-65.