基于多目標優化的汽車混合流水線平衡方法研究

曹守啟，朱雅雯

（上海海洋大學 工程學院，上海 201306）

0 引言

自從1913年福特公司開發出了世界上第一條流水線起，流水線作業逐漸成為汽車行業生產的唯一生產方式。隨著而來的便是流水線的平衡問題，這一問題最早由B.Bryton于1954年在他的碩士論文中提出，而在1955年Salveson首先建立了單品種裝配流水線的數學模型，并給出了模型的解法[1]，而自從20世紀80年代起，主要應用于飛機、汽車制造業的多品種的混合流水線得到了迅速發展[2]。這使得汽車行業從大批量、單一品種的生產方式，轉變為中多品種、小批量的精益生產方式。但由于混合流水線多品種的特點使得流水線平衡成為復雜的多目標問題。因此，流水線平衡成為混合流水線使用行業重要的關注點。流水線平衡系統由流水線平衡及流水線排產組成，用以協調各工位中不同型號車輛工藝數及各型號車輛投放順序來解決混合流水線效率問題的主流方法。目前對于混合流水線平衡的研究多著重在于流水線平衡而忽視流水線排產，在完成各工作站的車輛工藝平衡后直接根據各型號汽車需求量排產。但平衡與排產問題存在相互影響，單獨考慮平衡問題會降低優化效果。因此，目前對于平衡系統的研究多是獨立研究。而本文提出的合作性協同進化算法是一種能夠體現子目標間相互協作關系的多目標問題協同求解算法。其能夠有效，精確的解決如汽車混合流水線平衡系統這樣存在平衡與排產協作關系的多目標問題。

1 汽車混合流水線的多目標平衡

隨著汽車行業競爭與市場需求的變化，混合流水線的誕生時的流水線平衡問題變得更加復雜化。半個多世紀以來，混合流水線在汽車領域的使用已普及開來。但對于汽車混合流水線乃至所有混合流水線的設計，都將流水線的平衡與產品的投產排序分開作為兩種單獨的問題來考慮，但這樣的方式往往使得設計出現缺陷，無法得到最優解。這導致了混合流水線的使用停滯不前。現今的解決方式是將平衡設計與排產設計進行串聯考慮，在完成平衡設計后再參開排序設計。但這種方式并不能完全解決缺陷，如要得到全局最優解應把兩種設計并行考慮，在平衡的同時考慮排產，即將平衡問題看作多目標的優化問題。

1.1 以工作站負荷為基礎的混合流水線平衡

混合流水線的平衡只要分為三類：在流水線節拍已知的情況下，求得最少的線上工作站數；在已知不變的工作站數的條件下計算最小節拍；以及在節拍與工作站數都確定不變的基礎上均衡每個工作站的負荷。一般情況下，對于前兩類的平衡計算較少，這是由于如需對前兩者進行設計則設計投資、設備購買、場地規劃等等問題，屬于長期決策，一般在流水線建造設計之初就已確定。因此，本文中我們對于流水線的平衡問題主要考慮的是工作站的平均負荷，但汽車混合裝配流水線相較于普通生產單一產品的流水線，其平衡特點在于即使當平均負荷未超出標準的情況下單個型號產品也會出現超節拍的情況。而對于流水線平衡問題來說，其工作就是合理分配工作站工序，并使得每個工作站作業時間最大限度接近平均節拍，同時又能減少工作站的閑置時間與超載時間。

其中K為流水線負荷系數，F表示流水線上有效作業時間的總和，N表示流水線中的工作站數，C表示流水線的節拍（即流水線上生產兩件產品間的時間間隔）。

以一個擁有N個工作站的汽車混合流水線為例，線上共生產M種產品，產品的生產總量為D，每種型號汽車的需求產量為dm（m=1,2,3,…,M），對于以優化汽車混合流水線工作站負荷為目標的平衡工作來說，在滿足流水線節拍的條件下，在完成分配后希望其空閑時間最小，即使用節拍計算得到的理論工作時間與實際有效作業時間的相對誤差，用算式表達為：

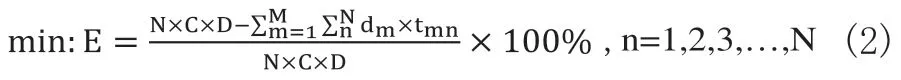
其中：

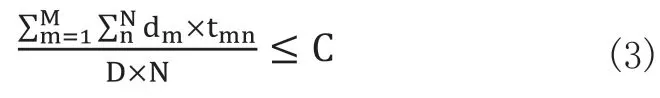
tmn為型號為m的產品在工作站n上的的作業時間；式(3)表示計算空閑時間的前提條件要求實際有效平均作業時間必定不能超過已定節拍值。

1.2 以工作站負荷為基礎的混合流水線排產

汽車混合裝配線的排產排序是屬于平衡系統的重要組成部分，隨著投產順序的改變，每種型號產品在同一工作站的節拍不盡相同，時常導致工作站中出現閑置或者超載的情況發生。而汽車混合裝配線的排產設計是基于流水線平衡的重要步驟，其決定了不同型號的產品在同一流水線上的投放順序，目的是保證產品的均衡化。對于汽車混合流水線排產，簡單的說來就是把各種型號的產品按照合理排序投送到流水線上，用算式可以這樣表達：在與平衡設計相同條件下，假設a為各型號產品生產dm的最大公約數，使得即M種類型產品在單次循環中每種類型產品的投產數量，一般情況下，對于流水線的排產就是對這單次循環中F個產品的排序。這樣循環a次，便是一條混合流水線的的排產結果。而在單次循環中的m種產品排序就要根據工作站最少空閑與超載的原則來計算。假設一條汽車混合流水線的移動速度為v，工作站n（n=1,2,…,N）的流水線長度為Ln，產品投產間隔為e，假設單次循環中第f位置的產品為m，m在工作站n的的工作時間tmnf流水線小于投產間隔則可能出現空閑狀態，考慮操作者走動速度vp，則空閑時間為：，假設混合流水線上第一輛汽車的起始位置為lml0=0，則第f位置車輛在工作站n上的位置為，考慮操作人員走動時間后的超載時間為：。則可用閑置與超載費用來體現排產效果，即目標函數為：

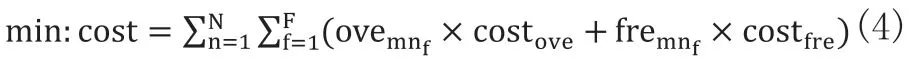
從上述模型公式中可以看到，汽車混合流水線的排產是基于產品在工作站中的工作時間進行計算的，即tmnf。而tmnf是根據流水線的平衡決定的各型號車輛在工作單元的作業要素決定的。因此，在一定程度上，流水線的平衡結果決定了排產結果。

2 汽車混合流水線平衡系統算法

2.1 汽車混合流水線獨立優化算法

汽車混合流水線平衡系統的兩個子目標為流水線平衡與流水線排產，兩者之間存在一定影響，一個子目標的改善會引起另一個子目標的變化。在一定程度上，流水線的平衡結果決定了排產結果，同時不同車型有著不同生產工藝，投產排序的不同會影響工作站上的工作時間，從而影響平衡效果，反之亦然。這樣的相互影響使得兩個子目標無法同時達到最優，只能協調子目標達到盡可能的最優化[3]，因此這是典型的多目標問題。

解決多目標問題的傳統方法有一個共同特征，即將多目標問題轉化為單目標問題進行求解，常見的化多目標為單目標的方法有加權和法、目標規劃法、E-約束法、目標滿意法等[4]。但多目標問題很難簡化為單目標問題，在簡化過程中難免收到主觀因素影響，這會大大影響優化結果。

而在20世紀50年代末，出現了一種進化算法，以模擬自然界的生物進化過程來進行優化的方法，之后在20世紀90年代中期得到迅速發展，是相較于傳統算法更為優秀的優化算法。其主要原理為，從隨機生成的種群出發，通過選擇、交叉、變異等進化來提高個體適應度。以此逐步逼近多目標優化問題的最優解集[3]。相較于傳統多目標優化方法，多目標進化算法在運行效率、精確度、分布型等方面都有了大大的提高，在工業、工程、科學等領域都有了大量的運用。但多目標進化算法無法完全滿足汽車混合流水線平衡系統的優化要求，由于平衡系統由兩個子系統組成，多目標進化算法無法體現兩個子系統之間的相互作用，單獨求解或者串行求解都無法得到系統整體最優解集。因此，考慮一種協同進化的算法，利用子系統間的系統關系進行并行求解。

2.2 汽車混合流水線協同優化算法

在1996年，Ehrlich和Raven在其發表的有關植物和昆蟲之間的協同進化時首次提出了協同進化遺傳算法(Coevolutionary Genetic Alorithm, CGA)[5]的概念。其將大型復雜問題分解，以子問題的形式存在，這些子問題存在協同關系，并行計算求解。這種算法模擬實際生態環境，各物種的進化過程具有一定關聯性而非獨立，物種間的進化相互影響，存在共生關系或者競爭關系，以這種角度考慮生物進化過程，即協同進化[6]。協同進化算法特點在于子系統間在相互作用下求得最優解，而汽車混合流水線的平衡系統是由流水線平衡與流水線排產共同組成，兩者相互影響，同時考慮才能得到最優解，因此適合使用協同進化算法進行求解。而協同進化算法又因為子種群間的不同協同關系分為基于生物間相互共生的合作型協同進化算法和基于種群間競爭的競爭型協同進化算法。其中競爭型系統優化算法體現了種群之間的對抗關系，以競賽的形式迫使種群進化；而合作型協同進化算法是模擬了種群之間的共生關系，即一方的進化需要另一方的幫助，這符合汽車混合流水線的平衡系統的實際情況。圖1為合作型協同進化基本框架。

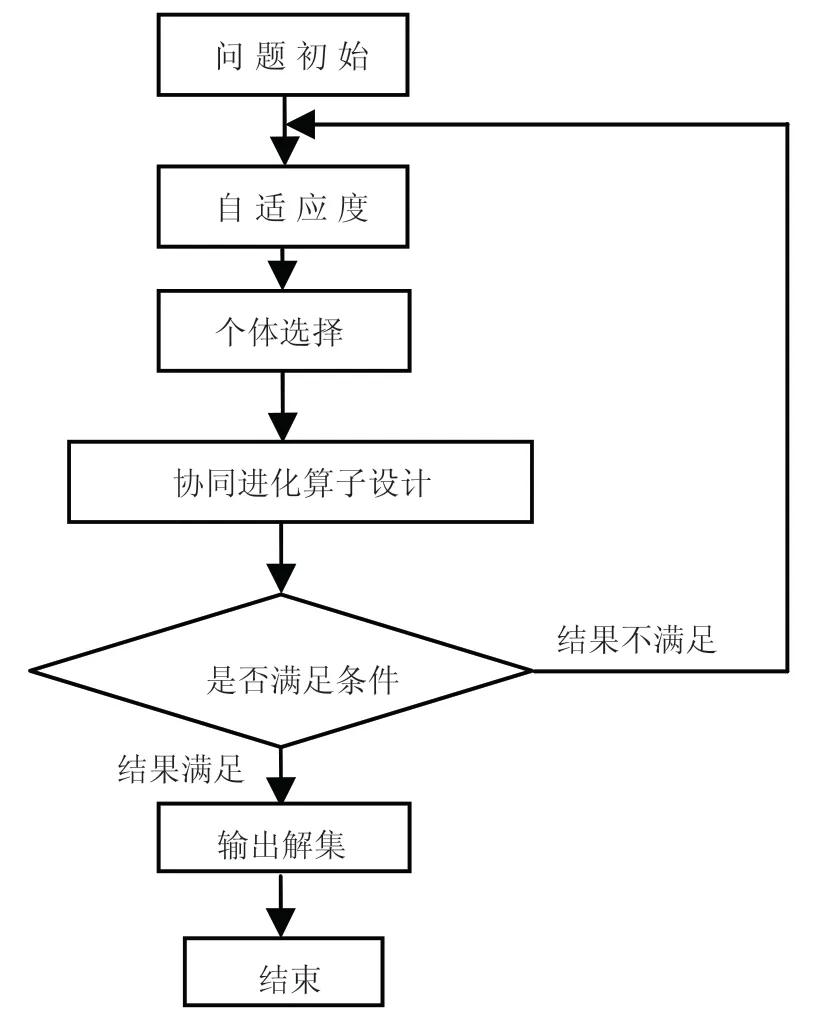
圖1 合作型協同進化基本框架

1994年Potter等提出了合作型協同進化算法，用來解決函數優化問題。由于該算法是以遺傳算法為基礎,所以稱其為合作型-協同遺傳算法[7](Cooperative Coevolutionary Genetic Algorithm, CCGA)。汽車混合流梳線使用合作型協同進化的核心思想是子群體間的協同合作關系，即將系統分解為2個變量組成的2個子群體，將一個子群體中的個體與另一個子群體中的代表體組成完整解，根據解的優劣評價個體與另一子群體的協同合作能力，如圖2所示。

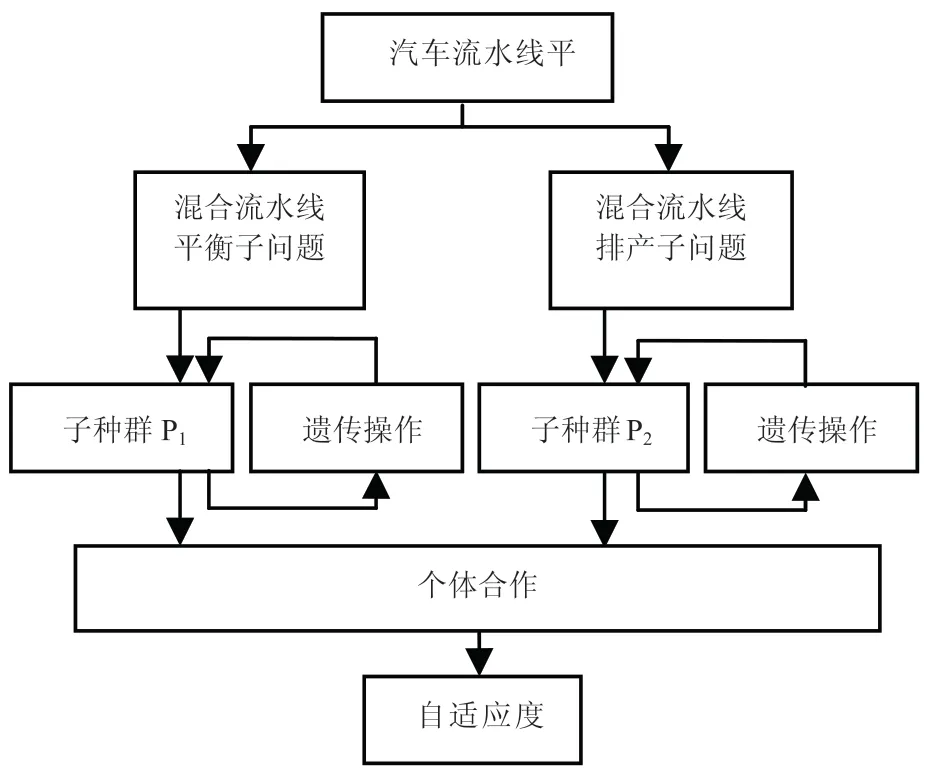
圖2 合作型協同進化圖

2004年Kuntinee Maneeratana[8]及AntonyW Iorio[9]等人將合作型協同進化算法引入已有的包括MOGA、NPGA、NSGA、CNSGA、NSGA -Ⅱ的多目標優化進化算法中。研究發現，使用合作型協同進化算法可以提高普通進化算法在多目標問題中的搜索效率。

3 結束語

隨著市場的需求變化，汽車混合流水線的應用變得迫切起來，混合流水線的平衡優化問題一直是其廣泛運用的困難之一。傳統的單獨對流水線進行平衡而忽略排產問題的算法存在一定問題。混合流水線排產與平衡是相互影響的兩部分，單獨考慮其中之一或串行的求解方式難以得到真正的最優解集。本文考慮將兩者進行并行求解，使用合作型協同進化算法對混合流水線這一多目標優化問題，為解決這一復雜優化問題提供了一個解決途徑。

[1] Kroo I Altus S,Braun R,eta.l Multidisciplinary optimization methods for aircraft preliminary design[R].AIAA,1994,94-4325-CP.

[2] Gokcen H,Erel E.A Goal Programming Approach to Mixed Model Assembly Line Balancing Problem[J].International Journal of Production Economics,24 January 1997,48(2)：177-185.

[3] 肖曉偉,肖迪,林錦國,肖玉峰.多目標優化問題研究概述[J].計算機應用研究,2011,3：28(3)805-808,827.

[4] Deb K,Agrawal S, Pratap A and Meyarivan T.A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization： NSGA II.[A].Parallel Problem Solving from Nature[C].(PPSN VI),Berlin,2000.

[5] Ehrlieh P R,Raven P H. Butterflies and plants：a study in coevolution[J].Evolution,1964,18(4)：586-608.

[6] 王磊.并行與雙系統協同差異進化算法及其應用[D].大連理工大學,2011.12.

[7] Potter M, De Jong K. A cooperative co evolutionary approach to function optimization[J].Lecture Notes in Computer Science, 1994,866(1994)：249-257.

[8] Kuntinee Maneeratana, Kittipong Boonlong and Nachol Chaiyaratana. Multi- objective Optimization by Co-operative Co-evolution[A].In Xin Yao eta.l editors, Parallel Problem Solving from Nature-PPSN VIII,Springer-Verlag, Lecture Notes in Computer Science[C].Birmingham, UK,September 2004,3242：772-781.

[9] AntonyW Iorio and Xiaodong Li A Cooperative Co evolutionary Multiobjective Algorithm Using non-dominated Sorting[A].In Kalyanmoy Deb eta.l editors,Proceedings of the Genetic and Evolutionary Computation Conference, Part I,Springer-Verlag, Lecture Notes in Computer Science[C].Seattle,Washington,USA, June 2004,3102：537-548.