基于輪球自平衡機(jī)構(gòu)的機(jī)器人設(shè)計(jì)
毛麗民,盧振利,朱培逸,劉叔軍
(常熟理工學(xué)院 電氣與自動(dòng)化工程學(xué)院,常熟 215500)
0 引言
自平衡機(jī)器人的概念源于二十世紀(jì)八十年代,基于倒立擺的模型,其系統(tǒng)是一個(gè)非線性、強(qiáng)耦合、多變量和自然不穩(wěn)定的系統(tǒng)[1]。
輪球自平衡機(jī)構(gòu)組成的機(jī)器人通過自身的平衡調(diào)節(jié)器,使其在球上近似平穩(wěn)的站立,實(shí)現(xiàn)動(dòng)態(tài)平衡。球與地面有一個(gè)微小的接觸點(diǎn),和一般的多輪車相比,單足平衡機(jī)器人靈活性更好。可以應(yīng)用到大型購物中心、際會(huì)議或展覽場(chǎng)所等領(lǐng)域,根據(jù)不同的應(yīng)用場(chǎng)合加入各類不同功能,例如加入避障、定位和網(wǎng)絡(luò)訪問控制,實(shí)現(xiàn)物體運(yùn)送的功能
1 機(jī)器人機(jī)構(gòu)及自平衡原理
1.1 機(jī)器人機(jī)構(gòu)
機(jī)器人結(jié)構(gòu)主要由主控制器、主框架、藍(lán)牙模塊、陀螺儀模塊、各類模塊等組成。機(jī)器人總高度為28cm;身長25cm,寬25cm;全向輪直徑5cm;球直徑18cm。機(jī)器人模型如圖1所示。
圖1中數(shù)字代表:1為構(gòu)架,2為電機(jī)驅(qū)動(dòng),3為主控制器獨(dú)立電源,4為OLED,5為主控制器,6為藍(lán)牙模塊,7為24V電源8為穩(wěn)壓模塊,9為總開關(guān),10為直流電機(jī),11為全向輪。
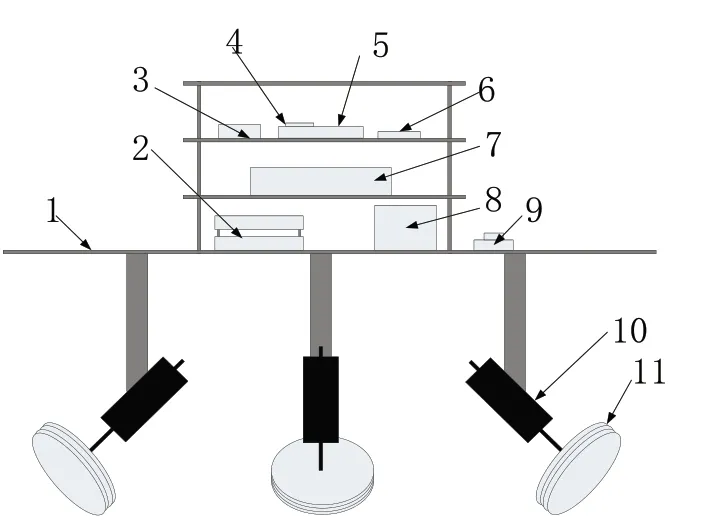
圖1 輪球自平衡機(jī)器人模型(無球部分機(jī)構(gòu))
根據(jù)上述模型,設(shè)計(jì)完成第一代輪球自平衡機(jī)器人(無球部分機(jī)構(gòu))樣機(jī)如圖2所示。

圖2 輪球自平衡機(jī)器人樣機(jī)
1.2 輪球移動(dòng)機(jī)器人自平衡原理
該機(jī)器人驅(qū)動(dòng)部分是通過三個(gè)電機(jī)驅(qū)動(dòng)的輪子,組成一個(gè)平面,彼此相差120度。該部分與球組成一個(gè)移動(dòng)機(jī)構(gòu),該球直徑應(yīng)該滿足R球>α*R萬向輪組, α為實(shí)驗(yàn)安全系數(shù),這里取1.414。
在機(jī)器人維持平衡過程中,由于變化的角度相對(duì)較小,把機(jī)器人的運(yùn)動(dòng)系統(tǒng)近似的看成平面,建立的運(yùn)動(dòng)模型如圖3所示。
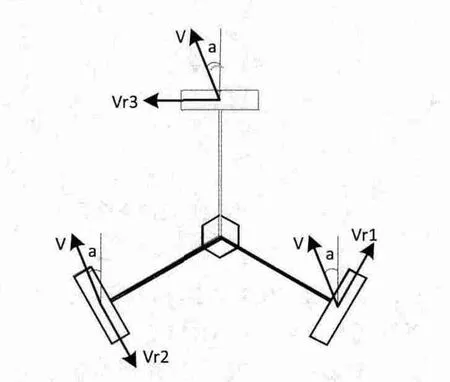
圖3 運(yùn)動(dòng)模型
模型中三個(gè)電機(jī)兩兩相隔120度,Vr是萬向輪運(yùn)動(dòng)正方向的運(yùn)動(dòng)速度,V是任意的某一方向的運(yùn)動(dòng)速度,a是V和0度線間的夾角,通過調(diào)節(jié)三個(gè)電機(jī)的轉(zhuǎn)速和正反轉(zhuǎn)合成V,由于本模型的建立是在剛性物體的基礎(chǔ)上,得到以下公式:

通過上述的數(shù)學(xué)模型,實(shí)現(xiàn)機(jī)器人在保持自平衡基礎(chǔ)上的二維運(yùn)動(dòng)。Vr1,Vr2,Vr3分別代表萬向輪系統(tǒng)中3個(gè)輪的轉(zhuǎn)速。
2 基于多傳感器設(shè)計(jì)機(jī)器人控制系統(tǒng)
本文設(shè)計(jì)的單足自平衡機(jī)器人,以STM32為控制核心,以MPU-9150實(shí)現(xiàn)姿態(tài)檢測(cè),得到角速度和角加速度,經(jīng)過卡爾曼數(shù)據(jù)融合得到真實(shí)的姿態(tài)值。通過PID算法對(duì)實(shí)時(shí)姿態(tài)值處理得到PWM波,對(duì)以F2807S為開關(guān)管的H橋電機(jī)驅(qū)動(dòng)進(jìn)行控制,以三號(hào)足球?yàn)闄C(jī)器人的單足,實(shí)現(xiàn)機(jī)器人在足球上保持平衡。利用OLED顯示屏實(shí)現(xiàn)人機(jī)交互,通過藍(lán)牙模塊進(jìn)行通訊。機(jī)器人多傳感器控制系統(tǒng)框圖如圖4所示。
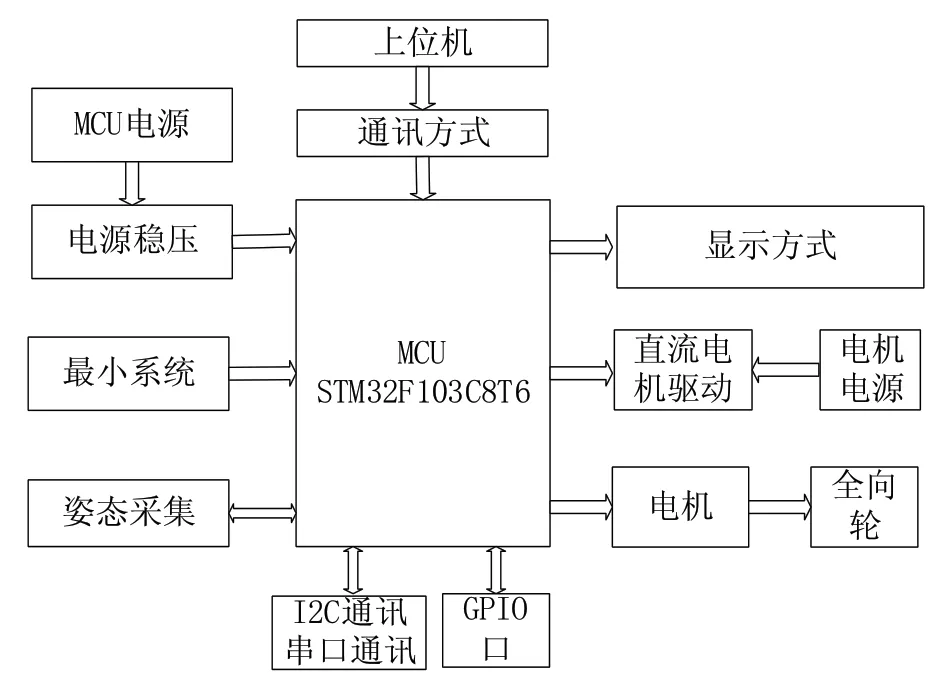
圖4 機(jī)器人多傳感器控制系統(tǒng)框圖
3 機(jī)器人多傳感器控制系統(tǒng)硬件設(shè)計(jì)
3.1 系統(tǒng)的供電電路設(shè)計(jì)
單足自平衡機(jī)器人的電源是3.7V的鋰電池,選用AMS1117三端穩(wěn)壓器將3.7V電壓轉(zhuǎn)成3.3V給單片機(jī)供電,如圖5所示。
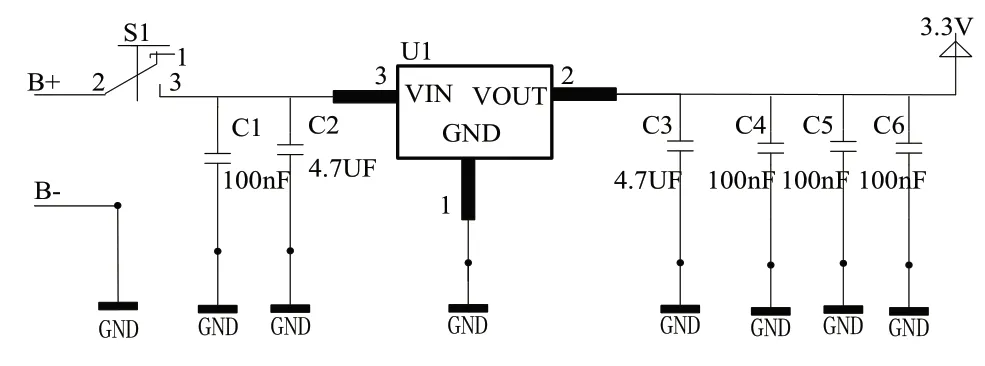
圖5 AMS1117-3.3V穩(wěn)壓電路圖
3.2 姿態(tài)檢測(cè)電路設(shè)計(jì)
輪球自平衡移動(dòng)機(jī)器人為保持平衡,需實(shí)時(shí)采集機(jī)器人的姿態(tài)值,在本設(shè)計(jì)選用MPU-9150姿態(tài)傳感器,通過對(duì)加速度值和速度值的處理可得到機(jī)器人的姿態(tài)值。姿態(tài)檢測(cè)電路如圖6所示。
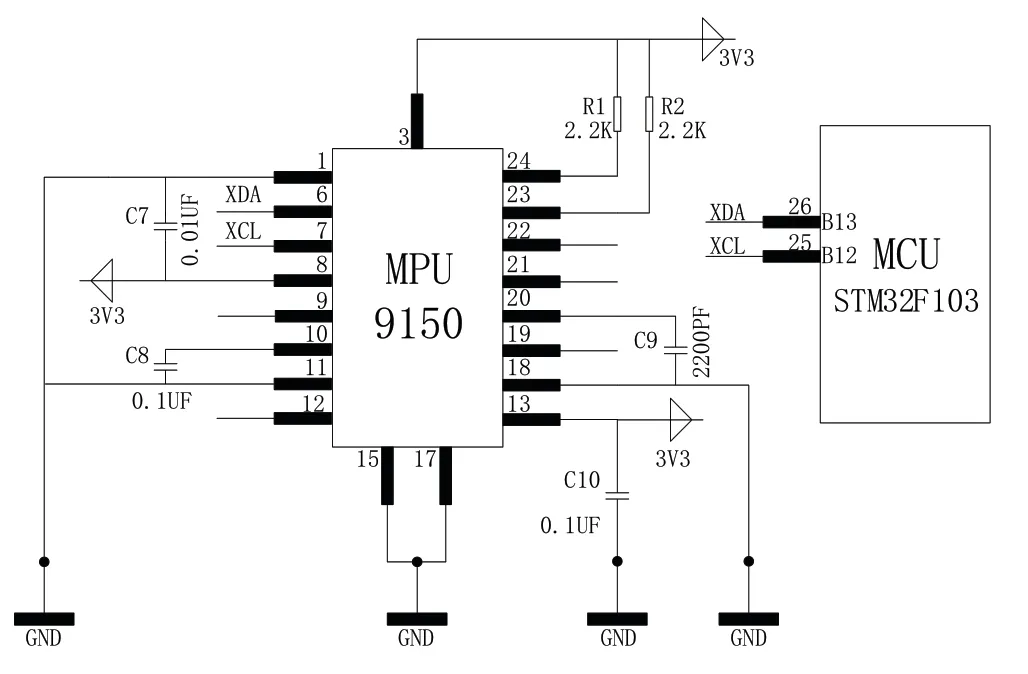
圖6 姿態(tài)檢測(cè)電路圖
3.3 電機(jī)驅(qū)動(dòng)電路設(shè)計(jì)
本文設(shè)計(jì)的電機(jī)驅(qū)動(dòng)電路是N溝道MOS管全橋電路,主要由控制電路和主電路組成,實(shí)現(xiàn)直流電機(jī)的加、減速和正反轉(zhuǎn)的功能。
圖7為電機(jī)驅(qū)動(dòng)信號(hào)邏輯電路圖,圖中控制電路使用與非門邏輯器,控制端口使用0和1來控制電機(jī)正反轉(zhuǎn),PWM波占空比來控制電機(jī)轉(zhuǎn)速,達(dá)到最優(yōu)的控制效果。
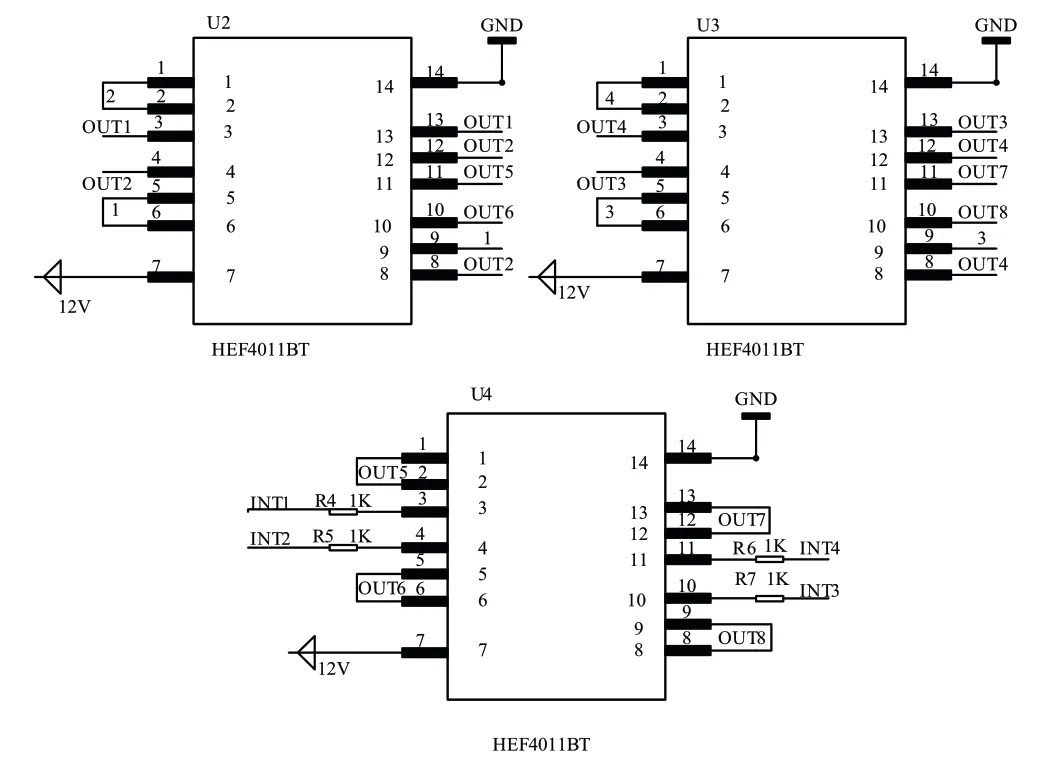
圖7 信號(hào)邏輯電路圖
圖8為電機(jī)驅(qū)動(dòng)主電路圖,圖中IRF2807S為MOS管,漏極電流為82A,最大電壓為75V。IR2104S是半橋驅(qū)動(dòng)器,使得電路可以無需脈沖變壓器驅(qū)動(dòng),得到所須的工作頻率,提高了電路的頻率穩(wěn)定性。
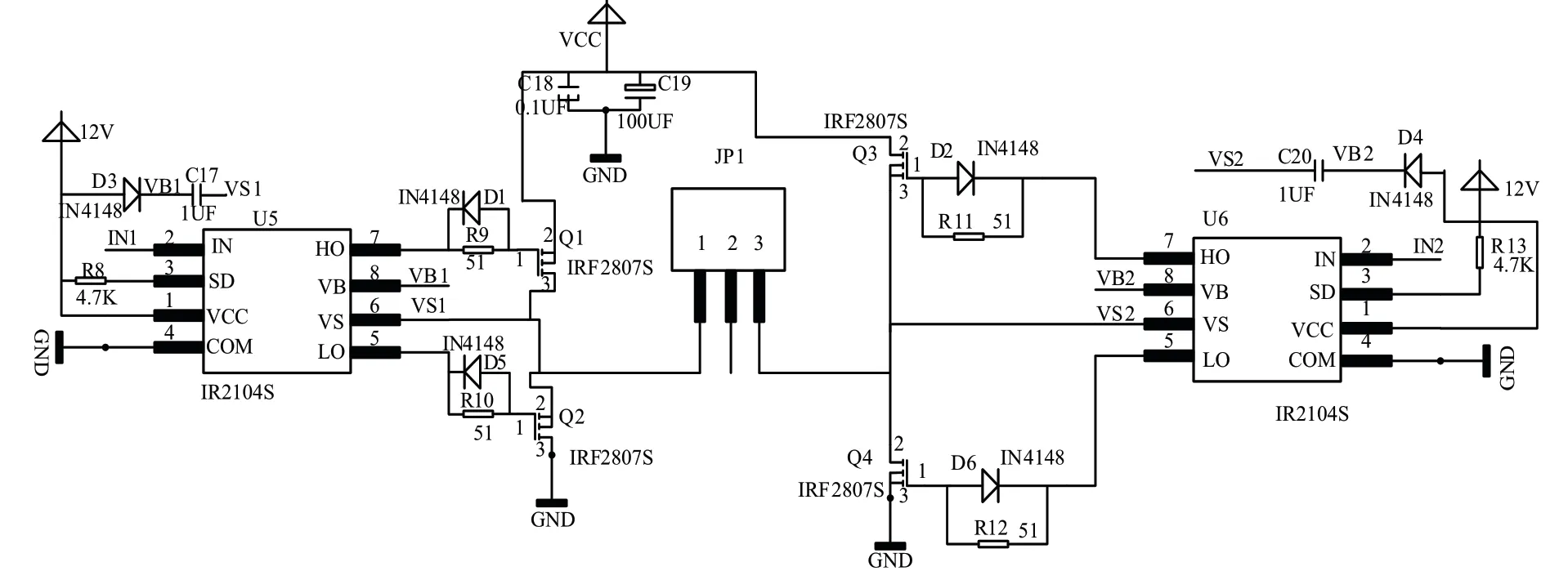
圖8 電機(jī)驅(qū)動(dòng)主電路圖
4 機(jī)器人多傳感器控制系統(tǒng)軟件設(shè)計(jì)
4.1 姿態(tài)檢測(cè)軟件設(shè)計(jì)
控制器通過I2C傳輸協(xié)議讀取姿態(tài)傳感器中的速度和加速度值,進(jìn)行處理,得出姿態(tài)角(傾斜角和航向角),流程如圖12所示。
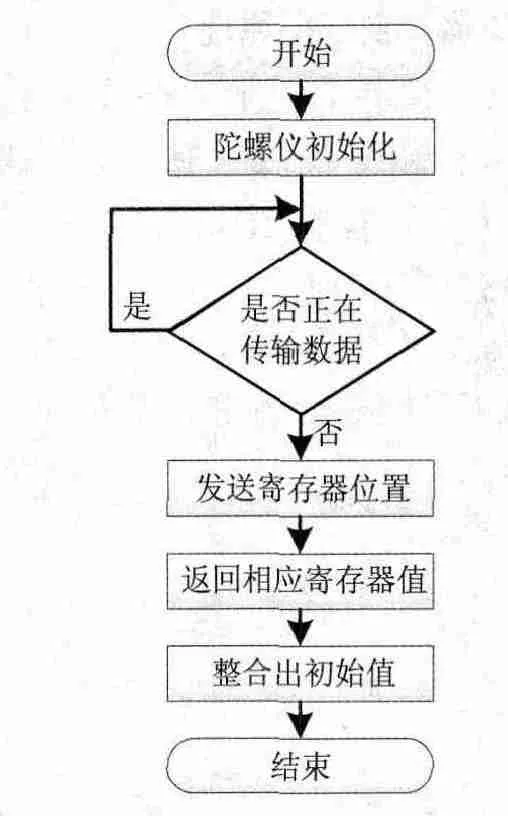
圖9 陀螺儀軟件設(shè)計(jì)流程圖

圖12 單足自平衡機(jī)器人調(diào)試
姿態(tài)傳感器程序中包括讀取相應(yīng)寄存器中的值和整個(gè)處理得出初始值兩個(gè)部分,其中BUF[12]是一個(gè)用于陀螺儀數(shù)據(jù)緩存的數(shù)組,ACCEL_XOUT_L、ACCEL_YOUT_L、ACCEL_ZOUT_L分別表示X、Y、Z軸的角加速度值得低八位數(shù)據(jù);ACCEL_XOUT_H、ACCEL_YOUT_H、ACCEL_ZOUT_H分別表示X、Y、Z軸的角加速度值得高八位數(shù)據(jù);GYRO_XOUT_L、GYRO_YOUT_L、GYRO_ZOUT_L分別表示X、Y、Z軸的角速度值得低八位數(shù)據(jù);GYRO_XOUT_H、GYRO_YOUT_H、GYRO_ZOUT_H分別表示X、Y、Z軸的角速度值得高八位數(shù)據(jù);A_X、A_Y、A_Z為整合處理后的角加速度初始值;G_X、G_Y、G_Z則為整合處理后的角速度初始值。
4.2 基于卡爾曼濾波器設(shè)計(jì)機(jī)器人姿態(tài)估計(jì)器
卡爾曼濾波器的控制主要有兩個(gè)方面:預(yù)測(cè)與更新。在預(yù)測(cè)時(shí),通過上一時(shí)刻狀態(tài)的判斷,計(jì)算出實(shí)時(shí)狀態(tài);在更新時(shí),實(shí)時(shí)觀測(cè)值使預(yù)測(cè)階段取得的測(cè)量值最優(yōu)化,得出最新估計(jì)值。卡爾曼濾波步驟如下:
1)先驗(yàn)狀態(tài)估計(jì):
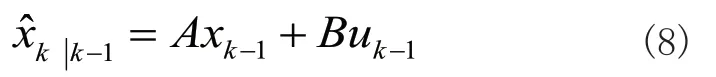
2)先驗(yàn)估計(jì)誤差協(xié)方差:
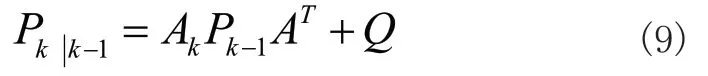
3)卡爾曼增益:
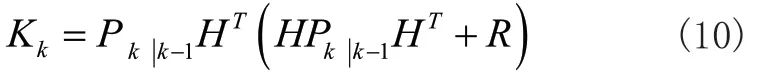
4)后驗(yàn)狀態(tài)估計(jì):
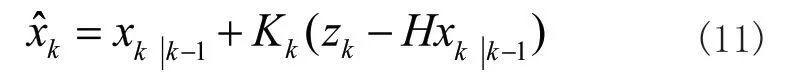
5)后驗(yàn)誤差協(xié)方差:
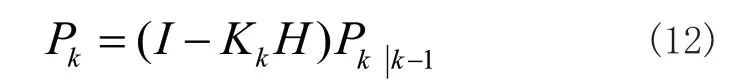
程序中使用公式Angle+=(Gyro_y-Q_bias)*dt計(jì)算出機(jī)器人某一個(gè)軸的角度,Q_bias表示陀螺儀輸出值與期望值之間的誤差,Angle就是系統(tǒng)預(yù)先估計(jì)值,然后得到觀測(cè)方程;但加速度傳感器采回的角度值A(chǔ)ccel就是類似于系統(tǒng)中的測(cè)量值,從而得出系統(tǒng)的狀態(tài)方程式。
Q_angle和Q_gyro各代表了系統(tǒng)對(duì)加速度傳感器及陀螺儀傳感器的信任程度。根據(jù)Pdot[0]=Q_angle-PP[0][1]-PP[1][0]計(jì)算出先驗(yàn)估計(jì)協(xié)方差的微分值,再把實(shí)時(shí)估計(jì)值進(jìn)行線性化計(jì)算。之后計(jì)算系統(tǒng)估計(jì)角度的協(xié)方差矩陣PP。計(jì)算卡爾曼增益K_0和K_1,K_0用于最優(yōu)預(yù)算值,K_1用于處理最優(yōu)預(yù)算值的偏差和刷新協(xié)方差矩陣PP。通過進(jìn)一步的計(jì)算得較真實(shí)的機(jī)器人姿態(tài)值。
4.3 PID控制器設(shè)計(jì)
4.3.1 PID控制器原理
PID因其簡單的結(jié)構(gòu)、較高的穩(wěn)定性和便于調(diào)整的特性,得到了廣泛的應(yīng)用。
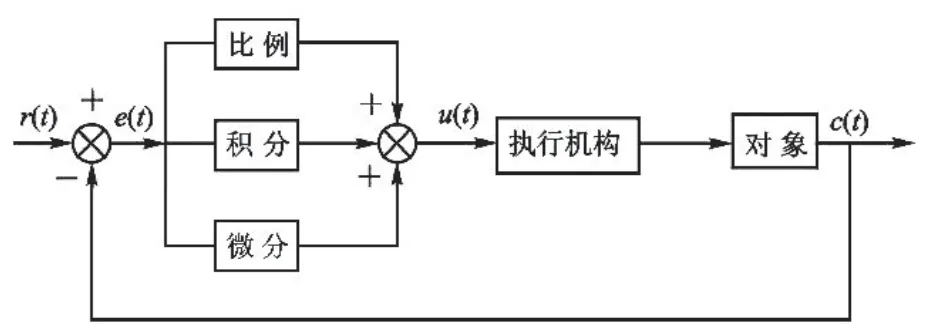
圖10 PID控制示意圖
上圖為PID控制示意圖,r(t)為輸入量;e(t)為穩(wěn)態(tài)誤差量;u(t)為PID輸出量;c(t)為實(shí)際輸出量。PID的輸入e(t)與輸出u(t)的等式為:
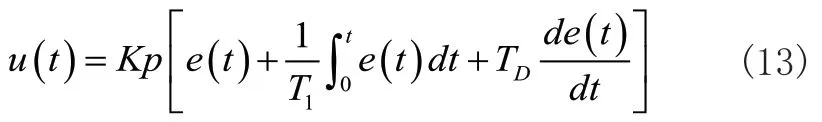
在式(13)中,Kp為比例系數(shù);T1為積分系數(shù);TD為微分系數(shù),PID調(diào)節(jié)器原理簡單、適應(yīng)性強(qiáng),實(shí)現(xiàn)自平衡機(jī)器人的控制方案是完全可行的。
4.3.2 PID控制器實(shí)現(xiàn)
在本系統(tǒng)中,Uk代表卡爾曼數(shù)據(jù)融合后機(jī)器人的實(shí)時(shí)傾斜角;U代表機(jī)器人直立時(shí)的傾斜角;ek為實(shí)時(shí)傾斜角度值與期望值的誤差;Kp、Ki和Kd分別為比例、積分和微分環(huán)節(jié)的系數(shù);Pp、Pi和Pd分別為比例環(huán)節(jié)、積分環(huán)節(jié)和微分環(huán)節(jié)增益量;P為PID輸出量,用來控制PWM波的占空比,實(shí)現(xiàn)電機(jī)的轉(zhuǎn)速控制。
5 基于多傳感器的機(jī)器人自平衡實(shí)驗(yàn)
5.1 卡爾曼濾波器參數(shù)設(shè)計(jì)
機(jī)器人在調(diào)節(jié)過程中會(huì)出現(xiàn)輕微的抖動(dòng),通過卡爾曼濾波使抖動(dòng)部分更為平緩。在對(duì)濾波器進(jìn)行調(diào)試的過程中,要對(duì)卡爾曼濾波器的陀螺儀、加速度傳感器的權(quán)值Q_gyro、Q_angle和卡爾曼增益R_angle設(shè)定參數(shù),設(shè)定完成后可發(fā)送數(shù)據(jù)到上位機(jī)顯示,如圖11所示。
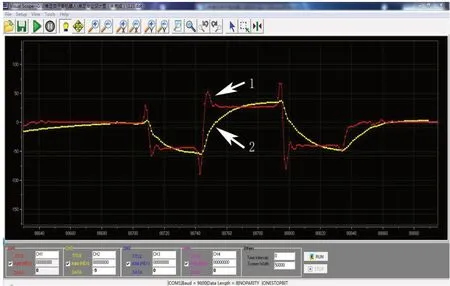
圖11 卡爾曼濾波調(diào)試圖
上圖為卡爾曼濾波調(diào)試圖,圖中1表示姿態(tài)傳感器原始曲線,2表示經(jīng)過卡爾曼濾波后的曲線。從圖可以看出,姿態(tài)值的初始曲線有很多的尖峰,噪聲比較大,經(jīng)過卡爾曼濾波后的波形比較的平滑,毛刺較少,可以比較精確的體現(xiàn)出機(jī)器人姿態(tài)的真實(shí)情況。
5.2 PID控制參數(shù)整定
通過實(shí)驗(yàn),比例調(diào)節(jié)能使自平衡機(jī)器人完成動(dòng)態(tài)平衡,但是響應(yīng)時(shí)間較長,同時(shí)在穩(wěn)定的位置不停地抖動(dòng),加入積分和微分調(diào)節(jié)使機(jī)器人的動(dòng)態(tài)偏差減小,縮短調(diào)節(jié)反應(yīng)時(shí)間。

圖13 單足自平衡機(jī)器人PID參數(shù)整定
PID參數(shù)的整定過程:第一步調(diào)整比例系數(shù)值的大小,使機(jī)器人能直站立起來,機(jī)器人在實(shí)現(xiàn)站立的過程中可能會(huì)伴隨著抖動(dòng)現(xiàn)象,第二步,將比例系數(shù)值降低到設(shè)定值的70%左右,小幅度的增大微分的系數(shù)值讓機(jī)器人可以穩(wěn)定的平衡。
6 結(jié)束語
面向服務(wù)型行業(yè)中對(duì)移動(dòng)機(jī)器人的需求,設(shè)計(jì)輪球自平衡機(jī)器人,應(yīng)用多傳感器實(shí)時(shí)檢測(cè)機(jī)器人位姿信息,應(yīng)用卡爾曼濾波算法對(duì)數(shù)據(jù)進(jìn)行優(yōu)化,通過整定PID控制器參數(shù)實(shí)現(xiàn)了該機(jī)器人的自平衡。實(shí)驗(yàn)結(jié)果表明該設(shè)計(jì)能使機(jī)器人在無干擾情況下實(shí)現(xiàn)自平衡,并通過有干擾自平衡實(shí)驗(yàn)表明了該控制器的魯棒性。該設(shè)計(jì)為機(jī)器人實(shí)用化提供了新的技術(shù)和方法。
[1] 張友民,戴冠中,等.卡爾曼濾波計(jì)算方法研究進(jìn)展[J].控制理論與應(yīng)用.1995(05).
[2] 陸如華,徐傳玉.卡爾曼濾波的初值計(jì)算方法及其應(yīng)用[J].應(yīng)用氣象學(xué)報(bào).1997(01):1-3.
[3] 陸芳,劉俊.卡爾曼濾波在陀螺儀隨機(jī)漂移中的應(yīng)用[J].微計(jì)算機(jī)信息.2007(23):12-16
[4] 張鵬飛,齊曉慧.基于N溝道MOS管H橋驅(qū)動(dòng)電路設(shè)計(jì)與制作[J].科技信息.2012(20):2-4.
[5] 張程.基于STM32的永磁同步電機(jī)驅(qū)動(dòng)器設(shè)計(jì)[J].福建工程學(xué)院學(xué)報(bào).2011(01):5-10.
[6] 張志強(qiáng).基于STM32的雙輪平衡車[J].電子設(shè)計(jì)工程.2011(13):19-25.
[7] 楊智,朱海鋒,等.PID控制器設(shè)計(jì)與參數(shù)整定方法綜述[J].化工自動(dòng)化及儀表.2005(05):25-27.
[8] 鄒凌,孫玉強(qiáng).基于卡爾曼濾波器的PID控制仿真研究[J].微計(jì)算機(jī)信息.2007(16):1-20.

