矩形石板優化排樣及切割路徑規劃研究
袁 哲,王永振,趙漢馳,安 冬
(1.沈陽建筑大學 機械工程學院,2.高檔石材數控加工設備與技術國家地方聯合工程實驗室,沈陽 110168)
0 引言
國內石材加工現處于粗放型的加工階段,多采用人工計算排樣和切割加工,石材利用率低,浪費了大量珍貴的不可再生資源[1]。為了提高石材的利用效率,有必要研制一種可自動排樣及切割加工的橋式切機,這需要對矩形石板的優化排樣及對應的切割路徑規劃問題進行研究[2~4]。國內外學者對矩形排樣進行了很多的研究,趙民[5]等利用VC++設計了矩形單一排樣系統;M.Z.Arslanov等[6]人利用多項式算法得到了同高度或同寬度矩形的最優排樣方式,并且得到了相應的最短路尋優路徑;Andrea Cassioli等[7]利用啟發式算法研究了同尺寸矩形在凸區域中的最優排樣方式。上述學者對矩形排樣有了深入的研究,并且給出了最短路尋優路徑,但是并沒有給出與排樣方式對應的切割方式及切割坐標,不能滿足橋式切機“一刀切”的特點。因此,針對石材“一刀切”的單一排樣方式以及切割路徑規劃方面還有待研究。
本文利用動態規劃算法建立單一排樣的數學模型,通過尋求動態規劃算法的全局最優路線,確定矩形石板的單一排樣方式,并且按照單一排樣的過程,尋找到矩形石板的切割路徑,提高了矩形石板的加工效率。
1 基于動態規劃的單一排樣數學模型的建立及求解
動態規劃是解決多階段決策問題的一種數學方法。動態規劃算法根據多階段決策問題的特點,把多階段的問題變換為一系列相互聯系的單階段問題,然后逐個加以解決的算法[8]。利用動態規劃算法求解多階段決策問題,必須先將問題的過程分為幾個相互聯系的階段,恰當的選取狀態變量和決策變量,并定義目標函數,把一個大問題化為一族同類型的子問題逐個求解,然后利用階段之間的遞推關系尋求全局最優路線。動態規劃算法所針對的問題有一個顯著的特征:它所對應的子問題樹中的子問題呈現大量的重復性。動態規劃算法的關鍵就在于對重復出現的子問題,只在第一次遇到時加以求解,并把答案保存起來,以后再遇到時直接引用,不必重新求解。矩形毛坯單一排樣就屬于這樣一類問題。
設矩形石板尺寸為L×W(L≥W),工程板尺寸為a×b(a≥b)。對于上述尺寸的矩形石板和工程板,利用動態規劃的思想,將整個決策過程分為L×W個階段,第x×y個階段的狀態變量為(x,y),決策變量為Q(x,y),目標函數為F(x,y),F(x,y)表示尺寸為x×y的矩形石板所包含工程板數量的最大值[9]。由動態規劃算法可知,F(L,W)為整個問題的目標函數。通過初始條件,按不同階段的遞推關系逐階段遞推尋優,確定F(L,W),并且通過逆推確定整個問題的最優路線,隨之確定矩形石板的單一排樣方式。矩形單一排樣動態規劃算法的數學模型為:

式中,
當F(x,y)=F(x,y-b)+int(x/a),矩形石板橫排,決策變量Q(x,y)=1 ;
當F(x,y)=F(x-b,y)+int(y/a),矩形石板縱排,決策變量Q(x,y)=2 ;
當F(x,y)=0,矩形石板排樣結束,決策變量Q(x,y)=0。
由于此問題的狀態變量是二維數組,為了不混淆第x×y階段與第y×x階段的狀態變量(x,y)與(y,x),故約定:第1階段狀態變量為(1,1),第2階段的狀態變量為(2,1),…,第L階段的狀態變量為(L,1),第(L+1)階段的狀態變量為(1,2)…,即先按x遞增,再按y遞增的方式來劃分不同的階段。
對于第x×y階段的目標函數F(x,y),若x<b或y<b,此時矩形石板不能容納一個工程板,故可得F(x,y)=0。對于矩形單一排樣,初始條件可以設為F(a,b)=1。由初始條件F(a,b)=1,根據F(x,y)的取值及與之對應的決策變量Q(x,y),從第a×b階段開始,利用動態規劃算法,求解出每個階段的目標函數及對應的決策變量。利用所求的目標函數數值與對應的決策變量,通過公式(1)逆推求解出包含最優解的最優路線。
例如,若第L×W階段的決策變量Q(L,W)=1,則此階段的目標函數F(L,W)=F(L,W-b)+int(L/a),由式(1),最優路線中的下一個階段為第L×(W-b)階段;查找第L×(W-b)階段的決策變量Q(L,W-b)的值,若Q(L,Wb)=1,則此階段的目標函數F(L,W-b)=F(L,W-2b)+int(L/a),由式(1),最優路線中的下一個階段為第L×(W-2b)階段;查找第L×(W-2b)階段的決策變量Q(L,W-b)的值,…,按照此種方式,直至找到Q(x,y)=0的階段,此階段即為最優路線結束的階段。至此,最優路線確定。
對于最優路線中決策變量,不妨設其值所組成的集合為數列{an}。顯然,{an}中的元素僅為1或2(不考慮結束時的0)。通過最優路線來確定整個矩形石板的單一排樣方式。例如,當{an}={1,1,2,2,2,1,1,2,2,1}時,則尺寸為L×W的矩形石板需要橫排,條帶長度為L,寬度為b,含工程板int(L/a)個;排完后的矩形石板尺寸為L×(W-b),此矩形石板需要橫排,所排條帶長度為L,寬度為b,含工程板int(L/a)個;排完后的矩形石板尺寸為L×(W-2b),此矩形石板需要縱排,所排條帶長度為(W-2b),寬度為b,含工程板int((W-2b)/a)個;排完余下的矩形石板尺寸為(L-b)×(W-2b),此矩形石板需要縱排,…,根據{an}中的元素,按照上述方式進行排樣,直至完成整個矩形石板的排樣。
2 矩形石板切割路徑的確定
矩形石板切割路徑的確定是通過記錄排樣過程中各根條帶的排樣方式來實現的。根據規范多級方式[10],整個矩形石板是由若干根條帶組成的,方向相同且連在一起的條帶組成級。為了盡可能的縮短切割路徑,實現橋式切機的自動化切割,需要將方向相同的條帶組成的級進行切割,然后再將級切割成條帶,再將切好的條帶切割成工程板,以此完成整個矩形石板的切割。
具體地說,矩形石板的切割分4步進行:
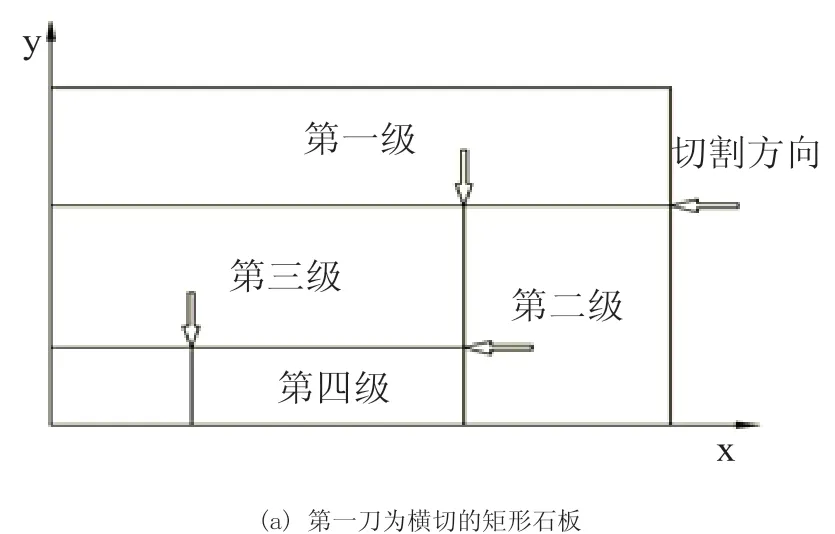
1)將矩形石板切割成級,如圖1所示。按照動態規劃算法中優化排樣的順序進行級的切割,將石材大板切割加工成幾個大的區域。每次切割完成后,利用橋式切機橫梁上的真空吸盤將級轉移至輔助工作臺,依次循環直至將最后兩個級切開后,將倒數第二級移至輔助工作臺。此時主切割工作臺上剩余最后一個級,以便將其加工成工程板。
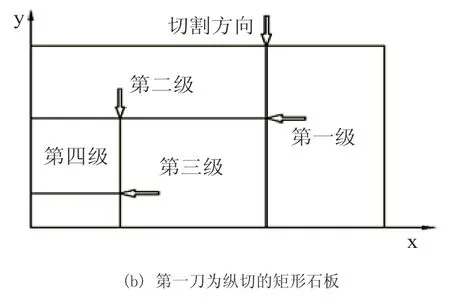
圖1 將矩形石板切割成級
2)將級切割成帶,如圖2所示。對于主工作臺上的級(此處以第一級為例),按照排樣方案進行條帶的切割加工,將級中的所有條帶切割加工出來。
3)將條帶切割成工程板,如圖2所示。步驟2完成后,將主切割工作臺旋轉90°,對主工作臺上的條帶(此處以第一級切割的條帶示例)按照排樣路徑進行通切,完成工程板的切割。
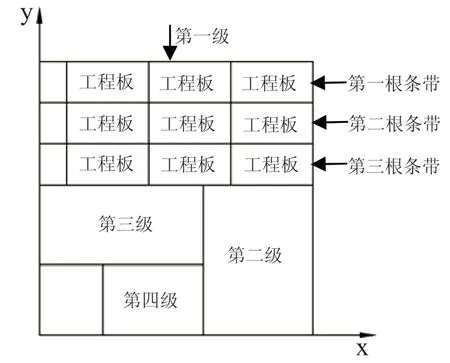
圖2 將第一級切割成條帶和工程板
4)完成主工作臺上的級的工程板切割加工后,通過真空吸盤將全部工程板移動至輔助工作臺,然后將上一個級移動至主切割作臺,并保持切割前的位置。對于主工作臺上的級,利用步驟2與步驟3的方法,將其切割成條帶與工程板。完成此級的切割加工后,通過真空吸盤將全部工程板移動至輔助工作臺,然后將上一級移動至主切割工作臺,并且保持切割前的位置,循環加工直至完成所有級的切割。
對于步驟1中級的尺寸,利用數列{an}來確定:考察{an}中連續子列的個數,連續子列的個數即為級的數目;每個連續子列中元素的個數代表相應級所包含條帶的個數。例如,{an}={1 1 2 2 2 1 1 2 2 1},此數列共有5個連續子列,對應的矩形石板有5個級:第一級為橫向級,包含2根條帶;第二級為縱向級,含有3根條帶;第三級為橫向級,含有2根條帶…。不失一般性,不妨設{an}中連續子列的數目為k,即此矩形石板分為k個級,第i(1≤i≤k)級的條帶數為ni根。
對于步驟1的切割,切割坐標與級的尺寸有密切關系。由圖1所示,每個級的尺寸與級在矩形石板中存在的次序有關。其中,級的寬度與級所含的條帶數有關,為ni×b。對于級的長度,第一級為橫向級的矩形石板(如圖1(a)所示),級的長度如下:奇數級第一級的長度為L,第三級的長度為(L-n2×b),第五級的長度為(L-n2×b-n4×b)… ,偶數級第二級的長度為(W-n1×b),第四級的長度為(W-n1×b-n3×b)…。對于第一級是縱向級的板材(對應于圖1(b)所示的矩形石板),有類似的結論。利用各個級的尺寸得到步驟1(將矩形石板切割成級)切割的坐標點如表1、表2所示。

表1 第一級為橫向級的矩形石板步驟1的切割坐標點

表2 第一級為縱向級的矩形石板步驟1的切割坐標點
對切好的級進行步驟2與步驟3的切割。對于要進行切割的級,若此級是橫級,則步驟2的切割全都是橫切,步驟3的切割全都是縱切;縱向級與橫向級恰好相反。
對于第一級是橫向級的板材,第一級步驟2切割需要切的刀數是(n1-1)刀,每一刀都是橫切。第1刀切點坐標為(L,W-b);第2刀切點坐標為(L,W-2b),…,第(n1-1)刀切點坐標為(L,W-(n1-1)×b)。按照此種方式切割,對第一級完成步驟2的切割。然后進行第一級步驟3的切割,此步驟的切割刀數與a和L之間的關系有關。若a能整除L,需要切割的刀數為(int(L/a)-1) ,產生int(L/a)塊工程板;若a不能整除L,需要切的刀數為int(L/a),產生的工程板數目為int(L/a)+1(其中最后一塊板材不是需要的工程板)。不失一般性,設第一級中步驟3的切割需要的刀數為m1,第i級中步驟3需要切割的刀數為mi(對于縱向級,有同樣的假設,但是切割的刀數需要考察a和W之間的關系),則第1刀切點的坐標為(L-a,W),第2刀的切點坐標為(L-2a,W),第3刀…第m1刀的切點為(L-m1×a,W)。按照上述方式切割,直至第一級切割完成。
對于其他的級,有上述的類似的結論。對其進行總結,結果如表3、表4所示。

表3 第一級是橫向級時,各級步驟2與步驟3的切割坐標點

表4 第一級是縱向級時,各級步驟2與步驟3的切割坐標點
3 實驗研究
設矩形石板尺寸為1500×1500,工程板尺寸為400×300,單位:mm。利用動態規劃得到的矩形單一排樣數學模型進行編程,得到矩形石板的切割路徑如圖3與圖4所示,切割坐標如表5與表6所示。

圖3 矩形石板步驟1的切割坐標
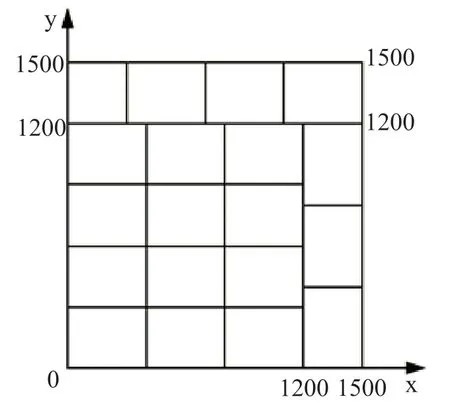
圖4 矩形石板步驟2與步驟3的切割坐標

表5 步驟1的切割坐標

表6 步驟2與步驟3的切割坐標
4 結論
1)通過動態規劃算法,建立了矩形單一排樣的數學模型,利用數學模型進行逆推得到了矩形工程板的最優排樣方案。
2)按照單一排樣各根條帶排樣的順序,得到了級的排樣,確定了橋式切機的切割路徑,實現了橋式切機的自動化切割,解決了石材企業人工下料慢,錯誤率高的問題,極大的提高了石材企業的加工效率,提高了石材企業的核心競爭力。
[1] 趙民,那麗紅,閔莉,等.基于圖像處理技術的石材大板表面輪廓提取算法[J].沈陽建筑大學學報(自然科學版),2010,26(5):981-985.
[2] 侯媛彬,高陽東,鄭茂全.基于貪心-遺傳算法的混合軌跡加工走刀空行程路徑優化[J].機械工程學報,2013,49(21):153-159.
[3] 劉恒.數控曲面切割路徑生成算法研究[J].制造業自動化,2010, 32(11):65-67.
[4] 胡鵬,胡春燕,蔣念平.二維激光連續切割移動材料路徑算法及約束[J].中國激光,2014,41(10).
[5] 趙民,王若男,李洪飛,等.基于VC++矩形紋理石材排樣系統[J].沈陽建筑大學學報(自然科學版),2011,27(3):578-582.
[6] M.Z.Arslanov,D.U.Ashigaliev,E.E.Ismail.Polynomial algorithms for guillotine cutting of a rectangle into small rectangles of two kinds[J].European Journal of Operational Research, 2008(185):105-121.
[7] Andrea Cassioli,Marco Locatelli.A heuristic approach for packing identical rectangles in convex regions[J].Computers & Operations Research, 2011(38):1342-1350.
[8] 曹衛華,郭正.最優化技術方法及MATLAB的實現[M].化學工業出版社,2005:112-115.
[9] 胡祥培,王旭茵,劉偉國,等.動態規劃問題的知識化數學模型生成器研究[J].管理工程學報,2004,18(2):64-70.
[10] 崔耀東,張春玲,趙誼.同尺寸矩形毛坯排樣的連分數分支定界算法[J].計算機輔助設計與圖形學學報,2004,16(2):252-256.

