串聯圓柱體氣動噪聲特性研究

馬 堯，寧方立

（1.中國民用航空飛行學院 航空工程學院，廣漢 618307；2.西北工業大學 機電學院，西安 710072）

0 引言

串聯圓柱體繞流氣動噪聲是飛機起落架氣動噪聲的基準算例[1]。對串聯圓柱體的非定常湍流流場和遠場氣動噪聲的研究，能夠為研究飛機起落架氣動噪聲奠定良好的基礎。因此，國內外對串聯圓柱體氣動噪聲進行了廣泛的研究。

Jenkins等[2～4]在NASA蘭利研究中心的QFF（Quiet Flow Facility）和BART（Basic Aerodynamic Research Tunnel）裝置中對串聯圓柱體的氣動噪聲進行了大量的試驗。Lockard[5]基于三維求解器CFL3D和FW-H（Ffowcs Williams-Hawkings）方程相結合的方法對串聯圓柱體氣動噪聲進行了仿真計算并與試驗結果進行詳細對比。Brès[6]基于氣體分子動力學理論，使用離散波爾茲曼方法（Lattice Boltzmann Method：LBM）和FW-H方程相結合的方法對串聯圓柱體的流場和聲場進行了仿真研究，得到了與試驗數據吻合的結果。但是LBM對計算機硬件的要求較高，計算量很大。Uzun[7]基于DDES（Delayed Detached Eddy Simulation）方法對兩種精度的網格進行了仿真計算。粗網格數量為3100萬，密網格數量為13300萬，是目前對串聯圓柱體最大網格量的數值仿真計算。通過與試驗結果和其他仿真結果對比，發現網格精度過高并不能得到更好的計算結果，相反對計算資源、計算時間要求更加苛刻。此外，法國ONERTA的Houssen，日本JAXA的Imamura，美國UCL的Marichal，NASA的Vatsa，Stanford的Yu，德國TUB的Greschner等也對這一基準算例進行了研究[1]。

在國內，劉敏[8]基于LES（Large Eddy Simulation）和FW-H方程相結合的方法對串聯圓柱體在不同間距比下的三維流場和氣動噪聲進行了仿真計算。隨著間距比的變化，流場呈現出三種不同的流態，其聲場也呈現不同的特點，在臨界間距比下，總噪聲值最大。趙良舉[9]通過LES求解非定常不可壓縮N-S方程獲得瞬態流場的聲源數據，基于FW-H方程及其積分解，計算由流動誘發的氣動噪聲，并比較不同流速、直徑、間距比對流場以及聲場影響。龍雙麗[10]基于LES和聲類比相結合的方法對不同雷諾數下二維圓柱繞流的遠場氣動噪聲進行數值計算。隨著雷諾數的增加，遠場的總聲壓級增大；最大聲壓級與流場的振蕩規律相關；減小雷諾數或者圓柱表面渦脫落引起的非定常脈動力能夠降低圓柱氣動噪聲。

現有研究多采用LES方法進行計算，本文使用DES（Detached Eddy Simulation）方法對串聯圓柱體的湍流流場進行仿真計算，然后用FW-H方程計算遠場氣動噪聲。將數值仿真計算結果與NASA蘭利研究中心的兩組基準試驗結果進行對比分析。通過改變間距比、圓柱體直徑、來流速度、攻角，探究不同參數對串聯圓柱體流場和氣動噪聲的影響，為飛機起落架的低噪聲設計提供參考。

1 基本方法及計算模型

本文對串聯圓柱體氣動噪聲進行仿真計算分為兩步：第一步：通過DES計算串聯圓柱體的非定常湍流流場，獲得流場分布和聲源數據；第二步：基于FW-H方程對串聯圓柱體表面的聲源數據進行積分計算，求得遠場氣動噪聲的分布情況。

以QFF裝置中串聯圓柱體為計算模型，定義坐標原點為前一個圓柱體的底部圓心位置，如圖1所示，來流方向與x軸同向。圓柱體的直徑D=0.05715m，兩個圓柱體的間距L=3.7D，流體從左向右流動，來流速度U=43.3m/s，密度ρ=1.225kg/m3，雷諾數Re=166000，流場參數與QFF基準試驗設置相同。

圖1 串聯圓柱體坐標系統

Lockard建議，將圓柱體展向長度取為3D，就可以捕捉到重要的湍流流動特征[1]。因此，本文以展向長度為3D進行計算。計算區域為長方體，沿流向長度為20D，法向長度10D，展向長度3D。圓柱體表面為無滑移邊界條件，展向邊界為周期性邊界條件，其余邊界為遠場壓力出口邊界條件。為保證網格質量，第一層網格距離圓柱體表面距離為5×10-6m，在兩圓柱體中間位置，適當加密網格，在遠場區域網格較為稀疏，網格單元總數約為150萬個。

采用Fluent軟件進行仿真計算，由于馬赫數低于0.3，故視為不可壓縮流動。選擇基于壓力的求解器進行計算，湍流數值模擬方法選擇DES方法，壓力和速度耦合采用SIMPLE算法，壓力差值算法為PRESTO！算法。時間和空間的參數采用二階精度的離散方法計算。

噪聲頻率受時間步長的限制，一個時間序列內做快速傅里葉變換（Fast Fourier Transform：FFT）的最高頻率為，最小計算頻率為。時間步長也受計算機硬件的限制，本節選擇時間步長tΔ=5×10-5s作為非穩態時間步長，每個時間步長內進行20次迭代計算。

為測量遠場噪聲，在圓柱體展向的中間平面上選取四個測量點，如圖3所示。各測量點距離兩個圓柱體中心的距離為2m，分別為來流方向上的測量點1，垂直于來流方向上的測量點2和4，以及后下游測量點3。

圖2 遠場聲場測量點位置

2 基準模型計算結果與分析

圖3是圓柱體中間截面位置處壓力系數Cp的數值仿真結果與試驗結果的對比。可以看出，數值仿真結果與試驗結果相當吻合。在圓柱體的迎風面位置，氣流直接撞擊在圓柱體上，此處氣流速度最小，壓力系數Cp最大。準確地計算壓力系數Cp能夠保證準確預測遠場氣動噪聲。

圖3 中間截面處壓力系數Cp的時均分布

圖4和圖5中將展向平面中間位置在y=0上的時均速度與文獻3中的試驗結果進行對比分析，圖4為圓柱體間的中心線上的速度時均分布，圖5為下游圓柱體尾跡區中心線上的速度時均分布。在圖5中，十字符號是低分辨率測量的試驗結果，而星號是高分辨率測量的試驗結果。通過與試驗對比可知，DES計算的結果與高分辨率的數值結果在數值上更為吻合，且變化趨勢是相同的。

圖4 兩圓柱間中心線y=0上速度時均分布

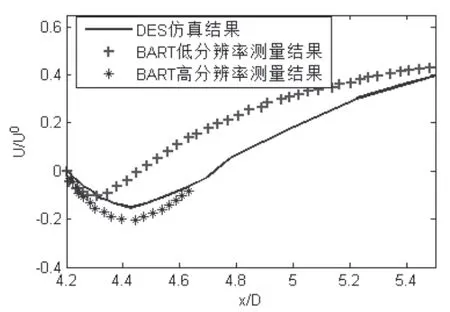
圖5 下游圓柱體尾跡區中心線上速度時均分布

圖6是QFF試驗中測量串聯圓柱體遠場氣動噪聲的位置，三個麥克風位于串聯圓柱體展向中間平面的位置，三個麥克風在該平面的物理坐標分別為：A (-8.33D，27.815D)、B (9.11D，32.49D)、C (26.55D，27.815D)。本文將對這三個測量點的氣動噪聲進行計算，并與QFF試驗結果進行對比分析。

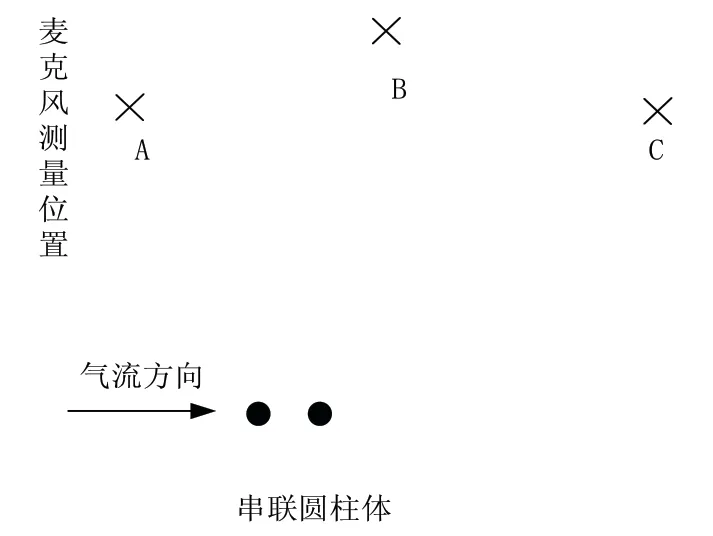
圖6 QFF試驗中麥克風測量點的位置

本文計算中串聯圓柱體展向長度為3D，而QFF中展向長度為16D，為了將這兩組結果進行對比，根據文獻[1]提出的聲學修正方法，假設數值計算中的展長為Ls，試驗模型的展長為Lc，采用聲學信息的疊加計算進行修正。將仿真計算的功率譜密度增加101g(Lc/Ls)dB進行修正后與QFF試驗結果進行對比分析，修正值為7.27dB。

圖7為本文仿真結果與QFF結果對比，數值仿真結果與試驗結果基本吻合。在基頻處（fs=185Hz）以及倍頻處（nfs,n=1,2,3…），出現峰值，基頻大小與QFF測得的串聯圓柱體旋渦脫落的頻率一樣，說明該噪聲是有規律的旋渦脫落引起的脈動壓力所引起的。串聯圓柱體噪聲幅值在較寬的頻率上數值較大，屬于不可忽略噪聲，是寬頻噪聲。

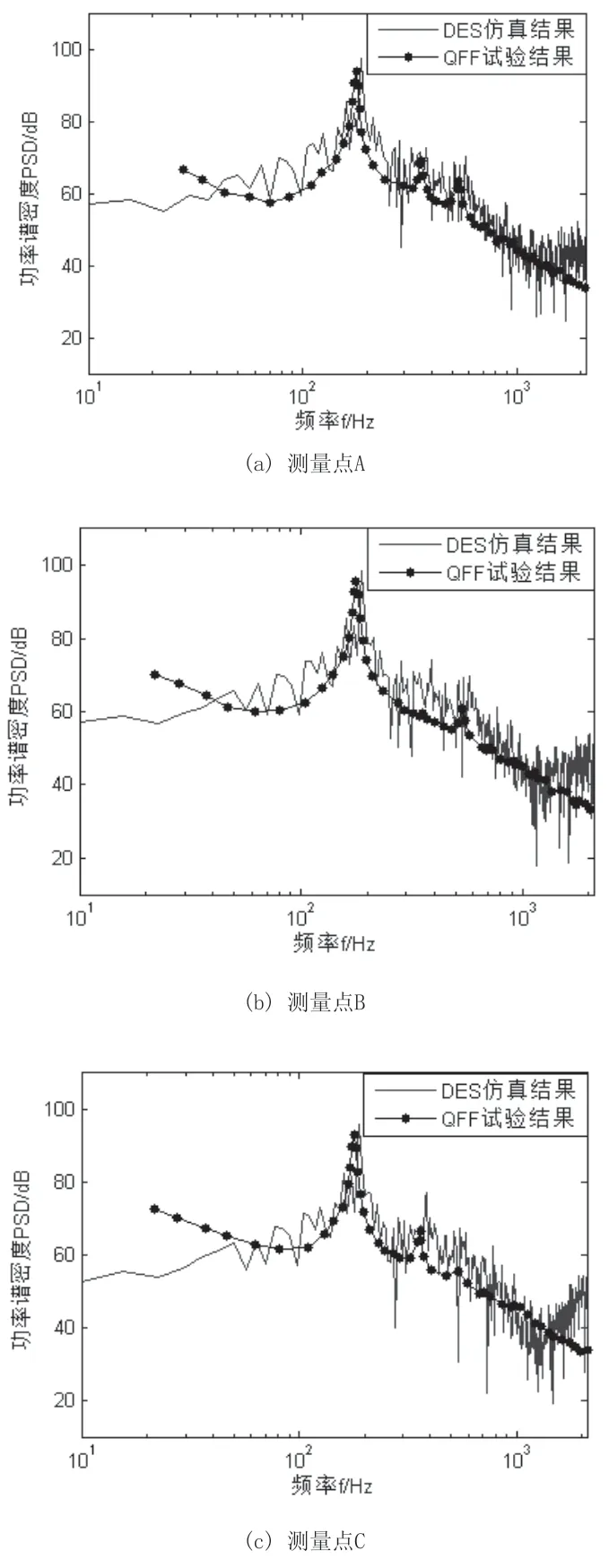
圖7 遠場輻射噪聲頻譜圖

由串聯圓柱體的流動特性可知，下游圓柱體的湍流更為劇烈，使得下游圓柱體產生更大的脈動壓力。圖8是分別以上、下游圓柱體為積分面計算的聲壓級在測量點B處的分布。可以明顯看出，下游圓柱體是整體噪聲最大的貢獻源。

圖8 串聯圓柱體各部件產生的噪聲對比

圖9是串聯圓柱體遠場氣動噪聲的指向性分布曲線。本文在展向中間截面上以O’(1.85D，0D)為圓心，以1m為直徑，每隔10°取一個點，共36個點，0o方向是來流撞擊到上游圓柱體所對應的位置。

圖9 遠場氣動噪聲指向性分布曲線

由圖9可明顯看出，串聯圓柱體的遠場氣動噪聲指向性具有典型的偶極子聲源“∞”特性。在來流方向上，總聲壓級較低，尤其是對應上游圓柱體迎風面位置處，總聲壓級最低。在垂直于來流方向上，遠場氣動噪聲較大。

3 不同參數對氣動噪聲的影響

3.1 不同間距比的影響

為探究串聯圓柱體間距比對氣動噪聲的影響，在U=43.3m/s，D=0.05715m，間距L=1.5D、3D、5D的情況下對串聯圓柱體氣動噪聲進行數值仿真計算。

由圖10可以看出，隨著間距比的變化，上游圓柱體剪切層后的氣流運動發生明顯變化。當L=1.5D時，由于間距較小，上游圓柱體沒有形成明顯的旋渦脫落，整個串聯圓柱體呈現出一定的單鈍體流動特性；當L=3D時，上游圓柱體后方形成的旋渦脫落增多，出現兩列明顯的交替旋渦，這些旋渦進一步撞擊在下游圓柱體上，此時圓柱體間的湍流流動非常強烈，下游圓柱體后面也出現交替的旋渦脫落；當L=5D時，上下游圓柱體均能產生旋渦脫落，相互影響作用已經減弱，上游圓柱體形成的旋渦有很大一部分自由發展，對下游圓柱體脈動作用力減弱。

圖10 不同間距比下渦量瞬態等值面圖

圖11為三個測量點處的總聲壓級隨間距比變化的趨勢，當L=1.5D時，總聲壓級最小，當L在3.7D~4.0D附近聲壓級最大，隨著間距比進一步增大，聲壓級開始減小。因此，串聯圓柱體存在一個臨界間距比，此時串聯圓柱體的總聲壓級最大。

圖11 不同間距比下測量點處總聲壓級

3.2 不同圓柱體直徑對噪聲的影響

以U=43.3m/s，L=3.7D為例，探究不同圓柱體直徑對串聯圓柱體氣動噪聲的影響。由前面的分析可知，下游圓柱體是最大的噪聲貢獻源。本節計算研究上下游圓柱體直徑變化對串聯圓柱體氣動噪聲的影響。在下游圓柱體直徑為D時，改變上游圓柱體直徑分別為0.5D、1.5D；在上游圓柱體直徑為D時，改變下游圓柱體直徑分別為0.5D、1.5D。

對測量點2處的氣動噪聲頻譜特性進行分析，如圖12所示。當上游圓柱體直徑為0.5D時，高頻處聲壓幅值增大，低頻處聲壓幅值降低，峰值位置右移；當上游圓柱體直徑為1.5D時，聲壓集中于低頻區域，串聯圓柱體呈現一定的單鈍體特性，噪聲明顯降低；當下游圓柱體直徑為0.5D時，測量點2處的聲壓幅值降低，且噪聲向高頻區域集中；當下游圓柱體直徑為1.5D時，聲壓級降低幅度十分明顯，噪聲主要集中在低頻區域。

圖12 不同直徑下測量點2處聲壓頻譜特性

因此，在臨界間距比下，通過改變圓柱體的直徑尺寸，可以有效降低聲壓級，改變噪聲頻譜特性。

圖13為不同直徑下的串聯圓柱體總聲壓級在測量點1、2、3處的對比，0.5D&D表示上游圓柱體直徑為0.5D，下游圓柱體直徑為D，其他直徑表示含義與此一致。通過對比可知，當上下游圓柱體直徑均為D時，總聲壓級最大，當下游圓柱體的直徑為1.5D時，總聲壓級最小。因此，在臨界間距比下，增大下游圓柱體直徑是最為有效降低串聯圓柱體氣動噪聲的方法。

圖13 不同直徑下測量點處總聲壓級

3.3 不同來流速度對噪聲的影響

以D=0.05715m，L=3.7D，U=10、20、40、43.3、60m/s為例，探究速度對串聯圓柱體氣動噪聲的影響。

在一定的雷諾數下，圓柱體斯特勞哈爾數St為常數，圓柱體繞流的渦脫落頻率fs與圓柱直徑D成反比，與速度U成正比，fs為最大噪聲所在的頻率值。在圖14和圖15中，隨著速度增大，氣動噪聲的聲壓級迅速增大，噪聲頻譜越來越向高頻區域集中，噪聲峰值位置有規律的增大。通過改變來流速度，能夠有效改變氣動噪聲的頻譜特性和噪聲幅值。

圖14 不同速度下測量點2噪聲頻譜特性

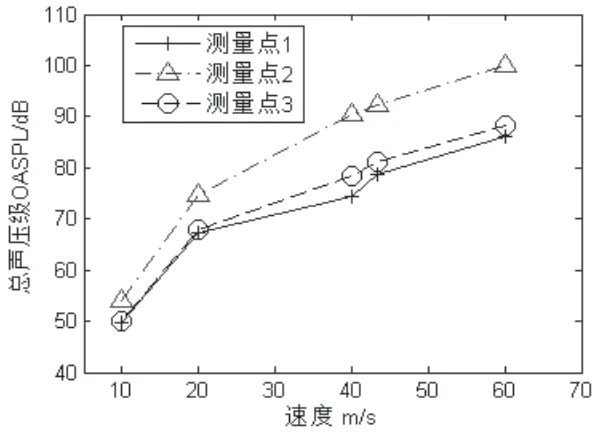
圖15 不同速度下測量點處的總聲壓級

3.4 不同攻角對噪聲的影響

本節計算研究在D=0.05715m，L=3.7D，U=43.3m/s時，不同攻角θ對串聯圓柱體氣動噪聲的影響。

圖16為不同θ時的瞬態渦量云圖，隨著θ增大，上游圓柱體形成的旋渦越來越少的撞擊在下游圓柱體上，在θ=5°時，有一部分氣流直接撞擊在下游圓柱體上，使得兩圓柱體間耦合作用減弱。當θ=10°時，上游圓柱體后方形成的旋渦很大一部分自由發展，沒有撞擊在下游圓柱體上，上下游圓柱體均呈現出一定的單個圓柱體繞流的特性。

圖16 不同攻角θ時瞬態渦量云圖

圖17是不同攻角θ時在各個測量點處的總聲壓級分布情況。當θ=1°，3°，5°時，頻譜的形狀沒有發生明顯改變，聲壓級逐漸降低；當θ=5°時，總聲壓級最小，同時在頻譜的倍頻處，聲壓級開始增大，說明一部分來流直接撞擊到下游圓柱體上；當θ=10°時，噪聲頻譜發生較大改變，幅值位置所在頻率降低，在倍頻位置處的聲壓級增大，且總聲壓級明顯增大，下游圓柱體呈現出一定的單個圓柱體繞流的特性。

圖17 不同攻角θ時測量點處總聲壓級

因此，通過適當改變攻角，可以降低串聯圓柱體的氣動噪聲，但攻角過大時，圓柱體間耦合作用減弱，呈現單個圓柱體流動特性，噪聲反而增大。

4 結論

串聯圓柱體氣動噪聲屬于寬頻噪聲，具有明顯的偶極子聲源特性，下游圓柱體對整體噪聲的貢獻最大。

串聯圓柱體存在一個臨界間距比L，這個值大約在3.7D～4.0D，此時圓柱體間流場耦合作用最為強烈，遠場氣動噪聲最大。若L值減小，串聯圓柱體呈現一定的單鈍體特性，湍流強度減弱，氣動噪聲降低；若L值增大，串聯圓柱體間的耦合作用也會減弱，呈現出一定的單個圓柱體流動特性，氣動噪聲也會降低。

改變圓柱體直徑大小能夠改變串聯圓柱體氣動噪聲的幅值和頻譜特性。通過對不同直徑的圓柱體流場和氣動噪聲特性進行對比可知，增大下游圓柱體的直徑是最有效地降低串聯圓柱體氣動噪聲的方法。

速度大小對串聯圓柱體的氣動噪聲幅值和頻譜特性有顯著的影響，并呈現出一定的規律性，減小速度對降低串聯圓柱體氣動噪聲幅值和改變頻譜特性非常有效。

合適的攻角大小，能夠減弱圓柱體間的耦合作用，降低串聯圓柱體的氣動噪聲。

[1] Lockard D. Summary of the Tandem Cylinder Solutions from Benchmark Problems for Airframe Noise Computationas-ⅠWorkshop[A].49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition[C]. Jan 2011,Orlando,Florida.

[2] Jenkins L, Neuhart D, McGinley C. Measurements of Unsteady Wake Interference between Tandem Cylinders[J].AIAA paper, 2006,2006-3202.

[3] Jenkins L,Khorrami M, Choudhari M. Characterization of Unsteady Flow Structures around Tandem Cylinders for Component Interaction Studies in Airframe Noise[J].AIAA Paper, 2005, 2005-2812.

[4] Hutcheson F,Brooks T. Noise Radiation from Single and Multiple Rod Configurations[A].12th AIAA/CEAS Aeroacoustics Conference(27th AIAA Aeroacoustics Conference)[C].May 2006, Cambridge, Massachusetts.

[5] Lockard D,Khorrami M,Choudhari M.Tandem Cylinder Noise Predictions[A].13th AIAA/CEAS Aeroacoustics Conference[C].May 2005,Rome, Italy.

[6] Brès G, Freed D,Wessels M. Flow and Noise Predictions for the Tandem Cylinder[J].Phys.Fluids.2012,24：036101,1-25.

[7] Uzun A,Yousuff H.An Application of Delayed Detached Eddy Simulation to Tandem Cylinder Flow Field Prediction[J]. Computers & Fluids.2012;60：71-85.

[8] 劉敏,劉飛,胡亞濤.三維串聯雙圓柱繞流氣動流場及聲場模擬[J].工程熱物理學報,2008(3)：403-406.

[9] 趙良舉,楊南奇,吳朵.橫掠二維串聯雙圓柱繞流氣動噪聲的數值模擬[J].重慶大學學報,2009(8)：943-949.

[10] 龍雙麗,聶宏,許鑫.不同雷諾數下圓柱繞流氣動噪聲數值模擬[J].聲學技術,2011,30(2)：111-116.