基于蓋帽模型的混凝土動態球型空腔膨脹模型和侵徹阻力分析

劉志林，孫巍巍，王曉鳴，馮君（.南京理工大學機械工程學院，江蘇南京0094；.南京理工大學理學院，江蘇南京0094）

基于蓋帽模型的混凝土動態球型空腔膨脹模型和侵徹阻力分析

劉志林1，孫巍巍2，王曉鳴1，馮君1
（1.南京理工大學機械工程學院，江蘇南京210094；2.南京理工大學理學院，江蘇南京210094）

為了獲得彈丸高速侵徹混凝土介質的阻力方程，提出了一種基于混凝土蓋帽模型的球形動態空腔膨脹模型。利用一般形式的狀態方程和屈服準則描述混凝土材料的動態力學特性，獲得了通用混凝土球形空腔膨脹模型的動態響應表達式。通過引入Dracker-Prager Cap屈服模型，在新的空腔膨脹模型中考慮了混凝土高壓下的屈服軟化特性。計算結果表明：采用帶剪切飽和的Mohr-Coulomb屈服準則與Tresca屈服準則推導出的阻力方程在高速階段與蓋帽模型差別較大。實驗結果證明：基于蓋帽模型的球形空腔膨脹模型因考慮混凝土高壓屈服軟化特性與實驗結果具有更好的一致性。

兵器科學與技術；侵徹力學；球形空腔膨脹；混凝土；蓋帽模型；阻力方程

0　引言

彈丸侵徹混凝土介質靶體的研究是近20年研究侵徹問題的熱點和難點，其研究方法一般有實驗法、數值仿真法和經驗法。其中，經驗法是用在大量實驗結果基礎上總結歸納出的經驗公式或半經驗公式預測侵徹深度等侵徹問題。因經驗公式使用條件苛刻等原因，工程計算中常使用半經驗公式來計算侵徹深度。半經驗公式的研究中最常見的是Forrestal等[1]提出的動態球形空腔膨脹理論，根據動態球形空腔膨脹理論計算侵徹阻力，再運用牛頓第二定律可較為方便地獲得彈丸侵徹深度。此種方法可預測不同侵徹速度下彈丸的侵徹深度，是彈丸侵徹混凝土介質的問題研究中十分重要的方法，在工程設計中發揮了極大的作用。相對于實驗法和數值仿真法，半經驗法效率高、費用低，因此，找到一種能夠預測侵徹深度的半經驗公式，在工程設計中顯得尤為重要。

半經驗公式中，侵徹阻力的計算是關鍵，動態球形空腔膨脹理論是常見侵徹阻力方程的理論研究方法。Forrestal等[1]采用線性混凝土壓力—體積應變關系和Mohr-Coulomb屈服準則，將混凝土球形空腔的動態響應區劃分為彈性區、開裂區和塑性區，建立了混凝土靶的動態空腔膨脹模型。李志康等[2]進一步發展了混凝土靶的動態空腔膨脹模型，將混凝土球形空腔的動態響應區域劃分為彈性區、開裂區和孔隙壓實區，其中孔隙壓實區的混凝土采用三段式線性狀態方程和考慮拉伸破壞帶剪切飽和的Mohr-Coulomb屈服準則描述，推導出了球形空腔動態膨脹響應的理論表達式[2-3]。目前，常用的Mohr-Coulomb準則并不能準確反映混凝土高靜水壓力下的體積屈服特性，因此無法精確地獲得彈丸在高速段的侵徹混凝土介質的阻力方程。

蓋帽模型起源于劍橋粘土模型[4]，后經過學者的發展和推廣，使之應用到巖石、混凝土、陶瓷及粉末等材料上[5]。引入蓋帽模型的目的是為了考慮靜水壓力導致的材料孔隙破壞，從而產生體積屈服現象。因此在靜水軸一端開口的剪切破壞面加上蓋帽封口以形成蓋帽模型，如Drucker-Prager剪切面與蓋帽的組合[6]。因此，在空腔膨脹理論中引入蓋帽模型是一種計算高速侵徹阻力的可行方案。

本文采用考慮高壓軟化效應的混凝土蓋帽屈服準則，結合HJC狀態方程[2，7]，建立考慮混凝土材料軟化效應的球形空腔膨脹理論，從而得到彈丸高速侵徹混凝土的阻力方程和侵徹深度。

1　動態空腔膨脹理論

1.1基本方程

動態空腔膨脹理論是基于連續介質力學的計算空腔在半無限介質中空腔膨脹速度與其表面壓力關系的理論計算方法，在球對稱條件下，Euler坐標系下的可壓縮動態球形空腔動態膨脹模型的質量、動量守恒方程[7]分別為

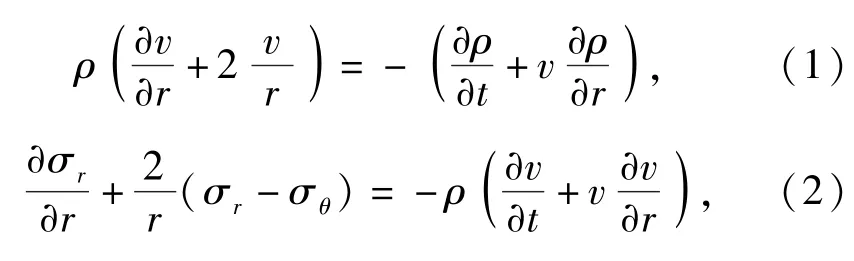
式中：ρ為密度；v為質點速度；r為極坐標；t為時間；σr和σθ分別為徑向和環向應力，取壓為正。

（1）式和（2）式的求解需先確立混凝土狀態方程和屈服準則，目前各種動態空腔膨脹理論的差別主要在于狀態方程和屈服準則的選擇[8]。為了方便推導，現給出狀態方程和屈服準則的一般表達式：

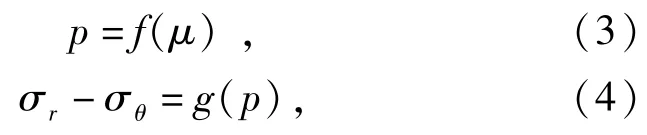
式中：體積應變μ=1-ρ0/ρ，ρ0、ρ分別為變形前、后的密度；p=（σr+2σθ）/3為靜水壓力。

因為球形空腔膨脹過程具有自相似性[7]，采用相似變換方法，將偏微分方程（1）式和（2）式化為常微分方程組來求解，引入相似變換ξ=r/ct、S=σr/f′c、 U=v/c，其中：c為響應區內側的界面速度；f′c為混凝土單軸抗壓強度。得到無量綱控制方程組的一般形式

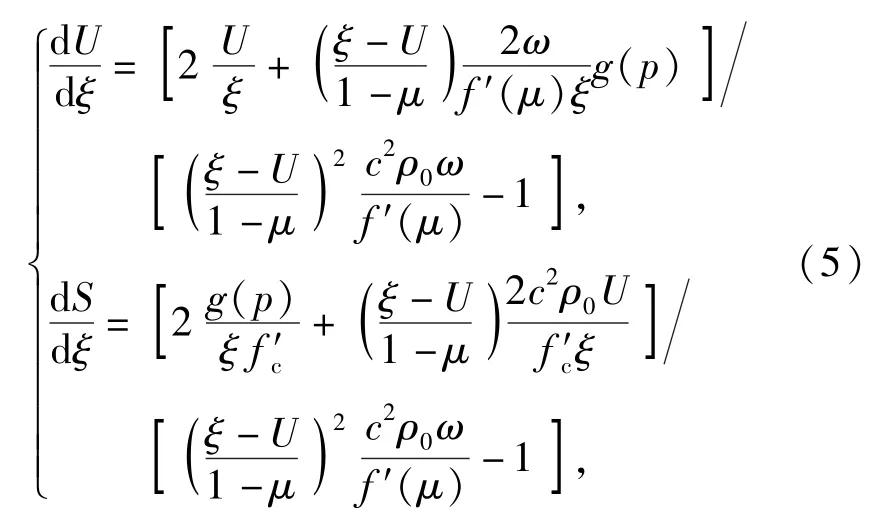
式中：f′（μ）=d p/dμ；ω=d p/dσr.

1.2狀態方程

本文采用HJC狀態方程[2，7]作為混凝土的狀態方程，HJC狀態方程將混凝土在其動態壓縮條件下的響應分為彈性區、孔隙壓實區、密實區。其中，彈性區和孔隙壓實區均為線性關系，密實區也可采用線性關系進行近似替代[2，9]。此時，三段式狀態方程（如圖1所示）可以用（6）式表示：

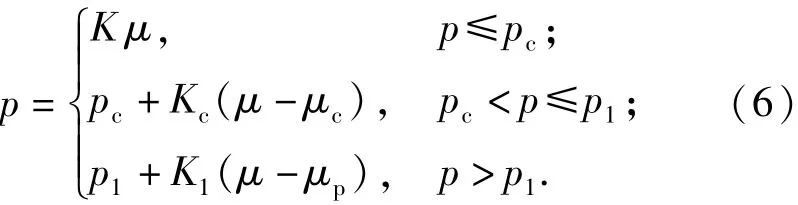
式中：K、Kc和K1分別為彈性區、孔隙壓實區和密實區的體積模量；pc=f′c/3為初始孔隙壓實壓力；p1為初始密實壓力；μc為孔隙初始壓實的體積應變；μp為初始密實體積應變。

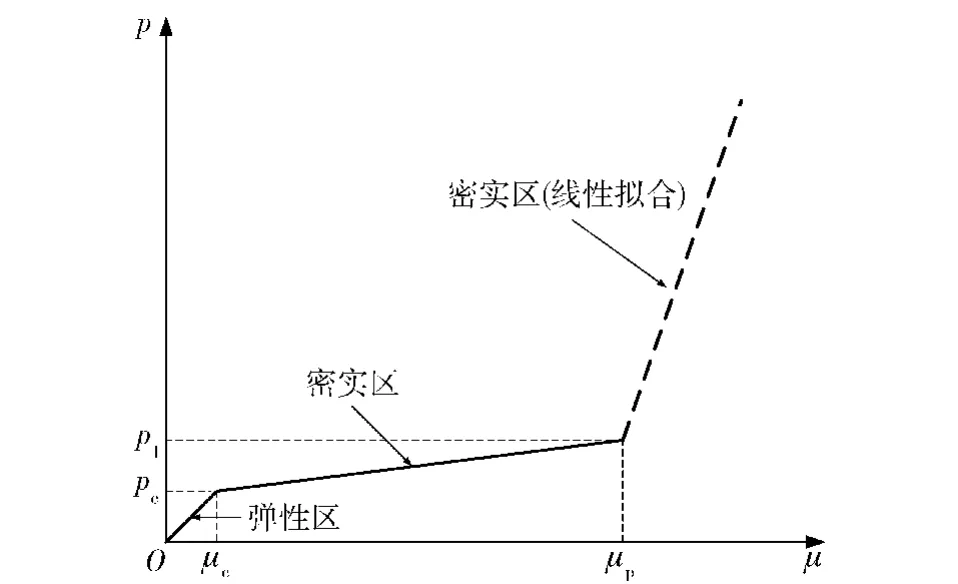
圖1　混凝土材料的狀態方程Fig.1　Equation of state for concretematerials

1.3屈服準則

本文引入Drucker-Prager蓋帽模型定義混凝土材料的屈服準則。蓋帽模型主要用于模擬巖石、混凝土和黏土類介質，目前已被嵌入Ls-dyna等動力分析程序[9]。蓋帽模型是基于固體力學中孔洞和裂縫效應的疊加原理而提出的本構模型。如圖2（a）所示，固體材料中只有孔洞時，屈服強度（蓋帽函數）在壓力較小時較為平穩，在高壓下下降較快，當孔洞完全壓實后，降為0；如圖2（b）所示，固體材料中只有裂縫時，裂縫間的摩擦力不斷增加，屈服強度隨著壓力的增加不斷提高；混凝土材料中同時存在孔洞和裂縫，因此混凝土最終的蓋帽模型屈服準則如圖2（c）所示。

考慮蓋帽的屈服準則和帶剪切飽和的Mohr-Coulomb屈服準則的主要差別在高壓階段，蓋帽模型考慮了混凝土高壓下體積屈服而產生的軟化效應。球對稱問題中的 Drucker-Prager蓋帽模型如圖3所示。與 Mohr-Coulomb類似，不同點在于Drucker-Prager蓋帽模型其高壓段考慮了蓋帽模型。本文根據Drucker-Prager蓋帽模型，對Mohr-Coulomb屈服準則進行改進，在Mohr-Coulomb屈服準則的高壓段加上蓋帽。

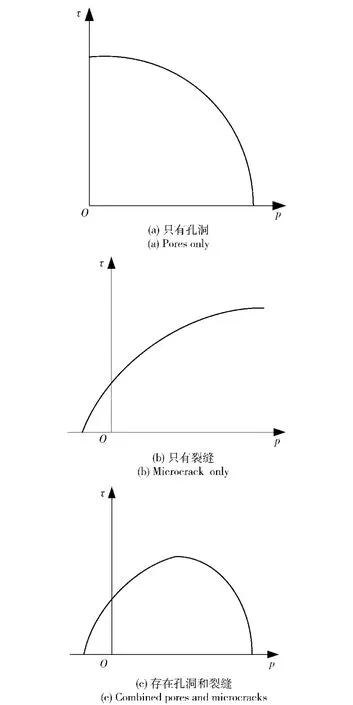
圖2　蓋帽模型Fig.2　Cap model

圖3　考慮蓋帽的屈服準則Fig.3　Yield criterion with cap

圖3中：λ為混凝土材料參數；pm為剪切強度峰值對應的靜水壓力；τ0=f′c（3-λ）/3為混凝土材料粘聚強度；R為材料常數，控制蓋帽的偏心距離；α為過渡面控制參數，控制剪切屈服面與蓋帽連接處的平滑度。剪切強度峰值對應的靜水壓力值根據（7）式[6]求得

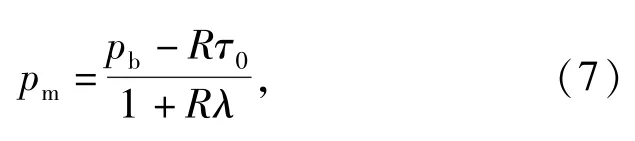
式中：pb為剪切強度降為0時對應的靜水壓力。

考慮蓋帽的屈服準則將混凝土在動態壓縮條件下的響應分為硬化區、軟化區和流動區。硬化區和軟化區的分界點為剪切峰值壓力pm，壓力值達到初始密實壓力p1時，蓋帽模型同時達到流動區，即pb= p1.混凝土的剪切峰值對應壓力一般不會超過初始密實壓力[10]，因此整個密實區的材料抗剪能力為0，本文稱此區域為密實流動區。而孔隙壓實區則劃分為兩個子區域，即硬化孔隙壓實區和軟化孔隙壓實區。

考慮到蓋帽模型非線性函數在空腔膨脹理論中計算的難度，本文對Drucker-Prager蓋帽模型中的蓋帽模型進行了修改，如圖3所示。將原有的非線性蓋帽模型進行了線性的簡化（即α取0），具體數學表達為

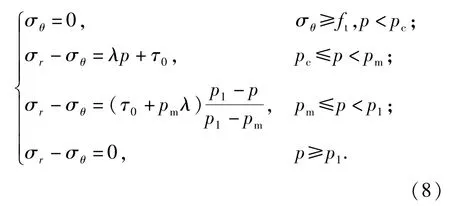
式中：ft為混凝土的單軸抗拉強度。

（5）式已給出了控制方程組的一般形式，只需將各響應區對應的屈服準則（8）式和混凝土狀態方程（6）式代入（5）式，便可得到各響應區控制方程組。這里只給出硬化孔隙壓實區和密實流動區的控制方程組（9）式和（10）式，其他響應區控制方程可類似得到，硬化孔隙壓實區控制方程組如下：

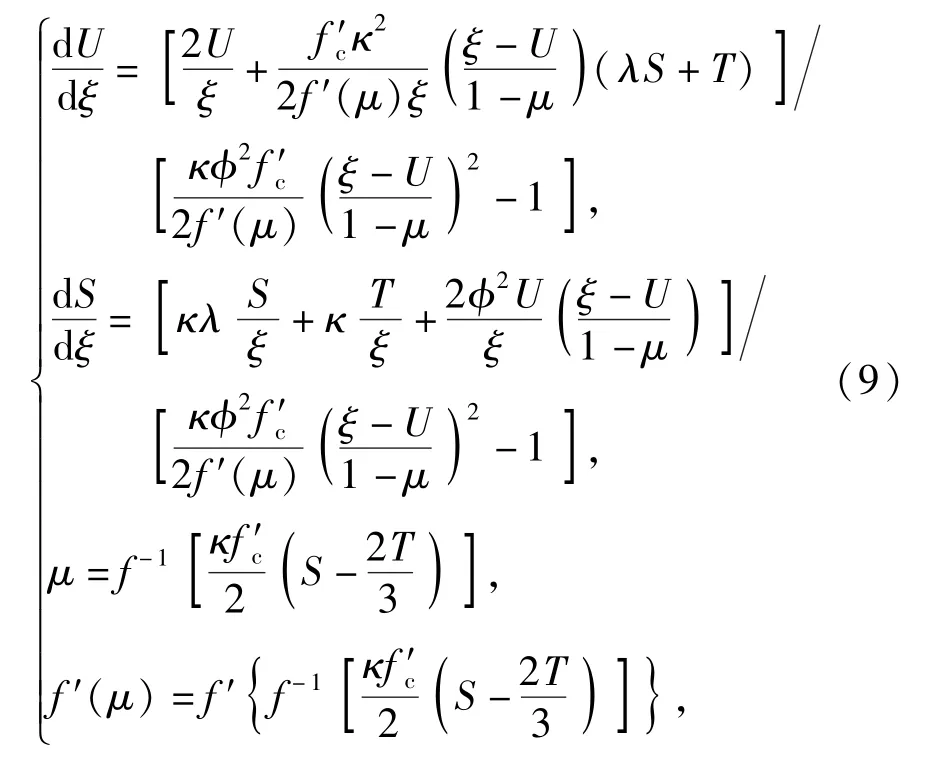
隨著靜水壓力增大，混凝土材料孔隙率逐漸降低，達到密實狀態時其抗剪能力幾乎為0，近似看成流體狀態。此時屈服準則取流動區段，即取λ=0，τ0=0.得到密實流動區的控制方程

1.4數值計算

根據上述的混凝土材料的狀態方程和屈服準則，將空腔膨脹響應區分成彈性區、開裂區、硬化孔隙壓實區、軟化孔隙壓實區、密實流動區，如圖4所示。

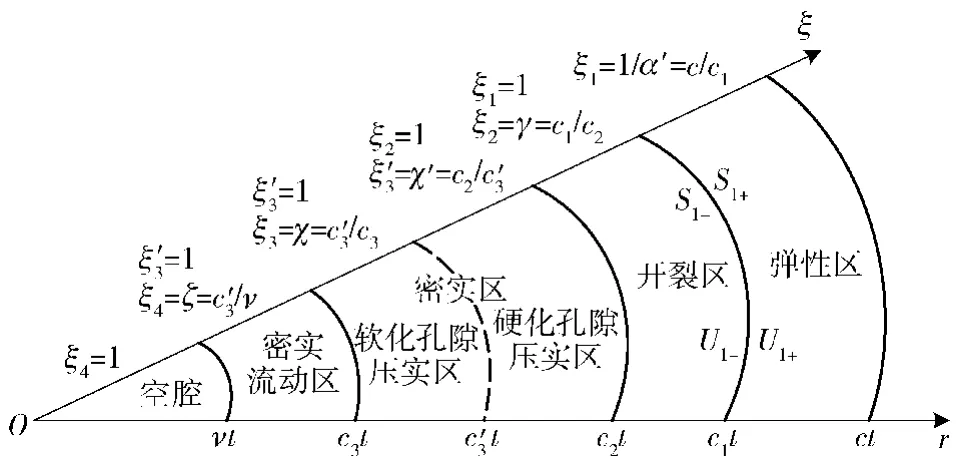
圖4　空腔膨脹響應區劃分Fig.4　Response region of spherical cavity expansion

彈性區和開裂區的控制方程組存在解析解[7]，而其他區的控制方程組不存在解析解，但根據屈服準則（8）式和Hugoniot間斷條件[2，6-7]，可得到硬化孔隙壓實區、軟化孔隙壓實區、密實區的界面上的邊界條件，再用Runge-Kutta Felhberg數值方法求解帶邊界條件的偏微分方程組。硬化孔隙壓實區、軟化孔隙壓實區和密實流動區的邊界條件分別為

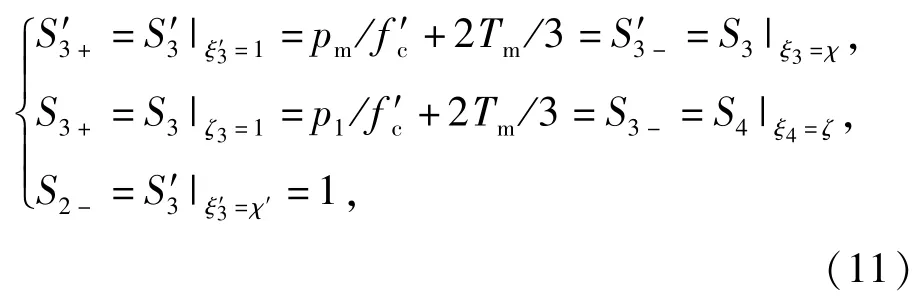
式中：Tm=τm/f′c，τm=τ0+λpm，τm為剪切峰值強度。

除了彈性區和開裂區有解析解外，其他區域并不存在解析解，且每個區域邊界內側的界面速度都是未知量。由于開裂區內側界面和彈性區內側界面上的質點速度和徑向應力均為開裂區界面波速與彈性區界面波速的比值的函數（即為α′的函數），為了求得整個響應區的控制方程，必須采用試算法。在給定的α′前提下求解，從而確定空腔膨脹速度V與空腔表面徑向應力σr（彈體阻抗）的關系，并按照 （12）式進行無量綱化擬合，確定常數A、B、C：

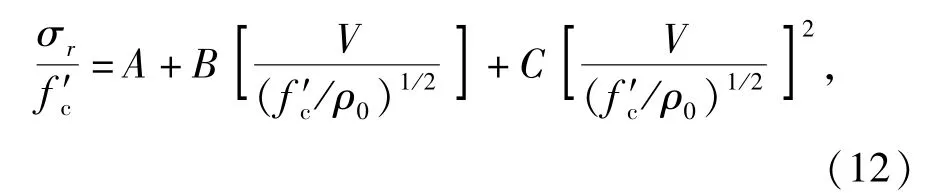
式中：A為靶材靜強度項的無量綱材料常數；B為靶材黏性效應項的無量綱材料常數；C為流動阻力項的無量綱材料常數[17]。

計算步驟如下：

步驟1 讀入基本參數，初始化各變量，給定空腔膨脹速度 V0、α′，根據彈性區和開裂區的解析解[7]計算S2+、U2+.

步驟2 若C1＞C2，則開裂區存在；否則，令C2=C1，此時開裂區消失。根據Hugoniot間斷條件計算U2-.

步驟3 用Runge-Kutta Felhberg數值方法求解硬化孔隙壓實區，獲得U′3+、S′3+、C′3.若U′3+=1，輸出空腔表面壓力S′3+，循環結束；否則根據Hugoniot間斷條件計算U′3-.如果C′3＜C2，硬化孔隙壓實區存在；否則，令C3′=C2，此時硬化孔隙壓實區消失。

步驟4 用Runge-Kutta Felhberg數值方法求解軟化孔隙壓實區控制方程組，獲得U3+、S3+、C3.若U3+=1，輸出空腔表面壓力S3+，循環結束；否則根據Hugoniot間斷條件計算U3-.如果C3＜C′3，軟化孔隙壓實區存在；否則，令C3=C′3，此時軟化孔隙壓實區消失。

步驟5 用Runge-Kutta Felhberg數值方法求解密實流動區控制方程組，獲得U4+、S4+.若U4+=1，且V0＜C3，輸出空腔表面壓力S4+，循環結束；否則返回步驟1.

根據文獻[3，10]中的混凝土材料參數的確定方法，確定混凝土材料參數，如表1所示。

根據空腔膨脹理論計算步驟，得到空腔膨脹速度與空腔表面徑向應力的關系，如圖5所示。按照（12）式的擬合結果為 A=9.036、B=0.856、C= 0.659.

表1　混凝土材料參數Tab.1　Parameters of concretematerial

圖5　無量綱空腔膨脹速度與徑向應力理論計算值及其擬合結果Fig.5　Dimensionless cavity expansion rate and calculated radial stress values and their fitting results

圖6為（12）式阻應力中各項占總應力的比例W隨空腔膨脹速度（0～1 700m/s）變化的關系。含系數A的靜態阻力項占總阻應力的大小隨著空腔膨脹速度的增大而逐漸減小，含系數C的流動阻力項的比例逐漸增大，含系數B的黏性阻力項的比例先增大后減小，且黏性項的比例最大都不超過15%.由圖6可看出：在空腔膨脹速度較低（小于250m/s）時，靜態阻力項起主導作用（W＞70%）；隨著速度的增加（約600 m/s），流動阻力項所占比例超過靜態阻力項；當速度大于1 100 m/s時，流動阻力起主導作用（W＞70%）.

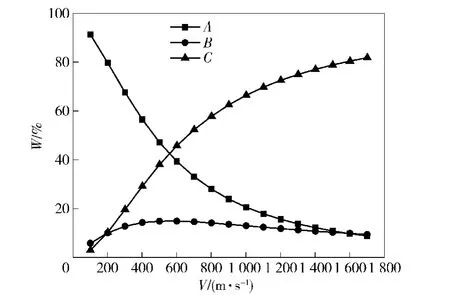
圖6　各項應力占總應力的比例隨著膨脹速度變化關系Fig.6　Relationship between the cavity expanding velocity and the percentage of each stress

空腔膨脹速度與各界面速度關系如圖7所示，隨著空腔膨脹速度的增大，整個混凝土響應依次出現下列分區：

1）彈性區—開裂區—硬化壓實區；

2）彈性區—開裂區—硬化壓實區—軟化壓實區；

3）彈性區—開裂區—硬化壓實區—軟化壓實區—流動密實區；

4）彈性區—硬化壓實區—軟化壓實區—流動密實區；

5）彈性區—硬化壓實區—流動密實區；6）彈性區—流動密實區。

圖7　空腔膨脹速度與界面速度及各分區的關系Fig.7　The cavity expanding velocity and interface velocity and the relationship amomg different partitions

本文比較了采用考慮蓋帽的屈服準則、Tresca屈服準則和考慮剪切飽和的Mohr-Coulomb屈服準則下的空腔膨脹理論計算的侵徹阻力，3種屈服準則如圖8所示。

Tresca屈服準則和考慮剪切飽和的Mohr-Coulomb屈服準則可表示為（13）式和（14）式：

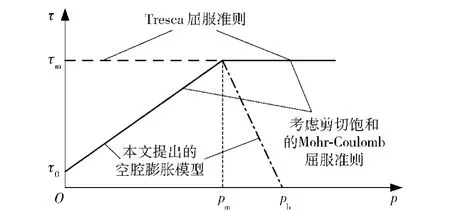
圖8　3種混凝土屈服準則Fig.8　Three kinds of concrete yield criteria

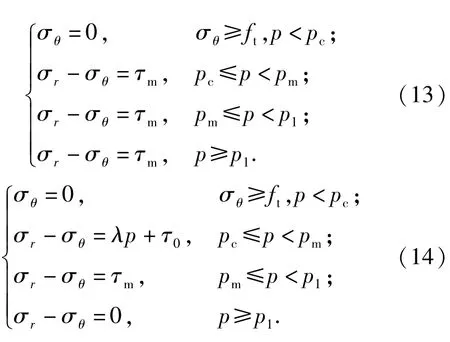
本文前面給出的控制方程組是含屈服準則函數和狀態方程函數的一般形式方程組，所以將（13）式或（14）式替代（8）式進行計算，即可得到Tresca屈服準則或考慮剪切飽和的Mohr-Coulomb屈服準則下的侵徹阻力。計算結果如圖9所示。

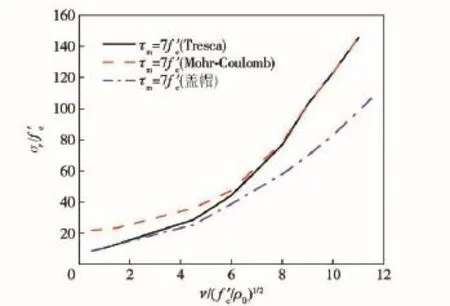
圖9　不同屈服準則下的阻力方程對比Fig.9　Comparison of resistance equations obtained from various yield criteria

由圖9可知，在空腔膨脹速度較低（無量綱速度小于3）時，考慮剪切飽和的Mohr-Coulomb屈服準則和蓋帽屈服強度準則計算的侵徹阻力差別很小，空腔膨脹速度較高（無量綱速度大于7）時，采用Tresca屈服準則和考慮剪切飽和Mohr-Coulomb準則的侵徹阻力差別很小，此時考慮蓋帽模型屈服準則的侵徹阻力明顯比Tresca屈服準則和考慮剪切飽和的Mohr-Coulomb屈服準則的侵徹阻力要小，且隨著空腔膨脹速度的增大，偏差越明顯。

2　實驗驗證

本文為了驗證阻力模型，實施了尖卵形彈丸高速侵徹混凝土靶板實驗。實驗中，使用105mm火炮作為發射平臺，彈丸撞擊速度范圍為800～1 400m/s，彈丸直徑2a=60.0mm，頭部卵形系數CRH=3.0；混凝土靶體強度等級為C40，實測150mm×150mm× 150mm立方體試塊單軸無側限抗壓強度 fcu= 46.8MPa（圓柱體強度f′c=0.8fcu=37.4MPa），ρ0= 2 300 kg/m3.實驗現場布置示意圖和發射前彈靶實物分別如圖10和圖11所示。

圖10　實驗布置示意圖Fig.10　Schematic diagram of experimental setup

侵徹實驗后回收的彈丸如圖12所示。可知，實驗后彈丸磨蝕和頭部變形情況與實驗前彈丸對比發現，彈丸侵蝕現象不明顯，質量損失量最大的撞擊速度為1 402m/s的彈丸（質量損失4.6%，長度縮短5%），其他撞擊速度下的彈丸質量損失和長度縮短量都較小，根據文獻[11-12]，此條件下的彈丸可按剛性彈處理。本文計算侵徹深度值按剛性彈模型來處理，不考慮彈丸質量損失和彈丸頭部形狀變化。

圖11　發射前彈靶實物圖Fig.11　Projectile and target before launch

圖12　實驗后的彈丸Fig.12　Projectiles after experiment

實驗與模型的驗證結果如表2所示。

表2　實驗結果對比Tab.2　Experimental results and calculated values

從表 2可看出：采用帶剪切飽和的 Mohr-Coulomb屈服準則預測的彈丸，侵徹深度在著靶速度小于1 060m/s時較為準確；速度大于1 060m/s后，預測的侵徹深度偏差較大，且誤差隨著撞擊速度的增加而增大（速度小于1 060 m/s時，誤差小于15%，速度1 402m/s時，誤差達30.6%），計算值都趨于保守，說明此速度下侵徹阻力預測值過大。Forrestal等[8]提出的工程經驗算法，計算值在速度1 150m/s時誤差小于15%，當撞擊速度再增加時，誤差也在繼續增大（速度為1 402 m/s時，誤差達22.2%），而本文提出的基于蓋帽模型預測的剛性彈侵徹深度和實驗結果符合較好（速度為995 m/s時，誤差為 15.2%，其他速度時的誤差都小于10%）.

3　結論

采用HJC模型三段線性狀態方程和考慮軟化效應的蓋帽屈服準則，建立了高速條件下可壓縮混凝土材料動態球形空腔膨脹理論。研究結果表明：

1）空腔膨脹速度較低時（無量綱速度小于3），帶剪切飽和Mohr-Coulomb屈服準則和蓋帽屈服強度準則下，計算的侵徹阻力差別很小。

2）空腔膨脹速度較高時（無量綱速度大于6），蓋帽模型下計算的侵徹阻力明顯小于Tresca屈服準則和考慮帶剪切飽和Mohr-Coulomb準則下的侵徹阻力計算值。

3）基于混凝土蓋帽屈服準則的空腔膨脹模型計算的侵徹阻力，在彈體高速侵徹（800～1 400m/s）預測的剛性彈侵徹深度和實驗結果符合較好。

（References）

[1]Forrestal M J，Tzou D Y.A spherical cavity-expansion penetration model for concrete targets[J].International Journal of Solids and Structures，1997，34（S31/S32）：4127-4146.

[2]李志康，黃風雷.混凝土材料的動態空腔膨脹理論[J].爆炸與沖擊，2009，29（1）：95-100. LIZhi-kang，HUANG Feng-lei.A dynamic spherical cavity-expansion theory for concrete materials[J].Explosion and Shock Waves，2009，29（1）：95-100.（in Chinese）

[3]李志康，黃風雷.考慮混凝土孔隙壓實效應的球形空腔膨脹理論[J].巖土力學，2010，31（5）：1481-1485. LIZhi-kang，HUANG Feng-lei.A spherical cavity expansion theory of concrete considering voids compacted effects[J].Rock and Soil Mechanics，2010，31（5）：1481-1485.（in Chinese）

[4]Roscoe K H，Schofied M A，Worth C P.On the yielding of soils [J].Geotechnique，1958，8（1）：22-53.

[5]盧應發，劉德富，田斌，等.廣義蓋帽模型和數值模擬[J].工程力學，2005（11）：9-14. LU Ying-fa，LIU De-fu，TIAN Bin，et al.Generalized cap model and numerical simulation[J].Engineering Mechanics，2005（11）：9-14.（in Chinese）

[6]Zhou R，Zhang L H，He B Y，etal.Numerical simulation of residual stress field in green power metallurgy compacts by modified Drucker-Prager cap model[J].Transactions of Nonferrous Metals Society of China，2013，23（8）：2374-2382.

[7]Stapathy S.Dynamic spherical cavity expansion in brittle ceramics [J].International Journal of Solids and Structures，2001，38（32）：5833-5845.

[8]Forrestal M J，Frew D J，Hanchak S J，et al.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].International Journal of Impact Engineering，1996，18（5）：465-476.

[9]Holmquist T J，Johnson G R，Cook W H.A computational constitutivemodel for concrete subjected to large strain，high strain rate，and high pressures[C]∥14th International Symposium on Ballistics.Quebec City，Canada：IEEE，1993：591-600.

[10]歐陽春，趙國志，夏衛國.空腔膨脹理論中混凝土材料模型的對比[J].解放軍理工大學學報：自然科學版，2005，6（5）：464-486. OUYANG Chun，ZHAO Guo-zhi，XIA Wei-guo.Investigation of materialmodels of concrete used in cavity expansion theory[J]. Journal of PLA University of Science and Technology：Nature Science，2005，6（5）：464-486.（in Chinese）

[11]Fossum A F，Brannon RM，Fossum A F，etal.The Sandia geomodel：theory and user's guide，SAND2004-3226[R].Sandia，US：Sandia National Laboratories，2004.

[12]Frew D J，Hanchak S J，Green M L，etal.Penetration of concrete targetswith ogive-nose steel rods[J].International Journal of Impact Engineering，1998，21（6）：489-497.

[13]Satapathy S.Application of cavity expansion analysis to penetration problems，I.AT.R-0136[R].Austin：University of Texas，1997.

[14]Canfield JA，Clator IG.Development of a scaling law and techniques to investigate penetration in concrete，NWL report 2057 [R].Dahlgren：USNavalWeapons Laboratory，1966.

[15]葛濤，王明洋，李曉軍，等.彈體沖擊混凝土半無限靶的侵徹阻力與深度計算[J].振動與沖擊，2008，27（1）：107-110. GE Tao，WANG Ming-yang，LI Xiao-jun，et al.Hydrodynamic model for concrete targets under impactof a projectile：resistance and depth of penetration[J].Journal of Vibration and Shock，2008，27（1）：107-110.（in Chinese）

[16]王明洋，鄧宏見，錢七虎.巖石中侵徹與爆炸近區問題研究[J].巖石力學與工程學報，2005，24（16）：2859-2863. WANG Ming-yang，DENG Hong-jian，QIAN Qi-hu.Study on problems of near cavity of penetration and explosion rock[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24（16）：2859-2863.（in Chinese）

[17]陳小偉，李小笠，陳裕澤，等.剛性彈侵徹動力學中的第三無量綱數[J].力學學報，2007，39（1）：77-84. CHEN Xiao-wei，LIXiao-li，CHEN Yu-ze，et al.The third dimesionless parameter in the penentration dynamics of rigid projectiles[J].Chinese Journal of Theoretical and Applied Mechanics，2007，39（1）：77-84.（in Chinese）

Spherical Cavity-expansion Model for Concrete Targets Based on Cap Model and Penetration Resistance Analysis

LIU Zhi-lin1，SUNWei-wei2，WANG Xiao-ming1，FENG Jun1
（1.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2.School of Science，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

In order to obtain the resistance equations of high-velocity projectile penetration into concrete targets，a dynamic spherical cavity-expansion model based on cap model is proposed.The general dynamic response expressions of concrete，which are applied to all kinds of spherical cavity expansionmodel，are obtained by describing the dynamicmechanical behaviors of concretematerialwith general equation of state and yield criterion.Yield softening properties of concrete under high pressure are considered in the proposed cavity expansion model by introducing the Drucker-Prager cap model.The calculated results show that the resistance equations of high velocity stage derived using Mohr-Coulomb yield criterion with shear saturation and Tresca criterion are great different from those derived using the cap model.The predictions obtained from the cap model are in good agreementwith experimental data.

ordnance science and technology；penetration mechanics；spherical cavity expansion；concrete；cap model；resistance equation

O385

A

1000-1093（2015）12-2209-08

10.3969/j.issn.1000-1093.2015.12.001

2015-05-11

國家自然科學基金項目（51308297）；國家重點基礎研究發展計劃項目（2011年）

劉志林（1988—），男，博士研究生。E-mail：liuzhilin1017@163.com；王曉鳴（1962—），男，教授，博士生導師。E-mail：202xm@163.com