單部件劣化系統(tǒng)的維修成本優(yōu)化研究
(中南大學(xué)商學(xué)院 湖南長(zhǎng)沙410083)
一、引言
隨著技術(shù)的進(jìn)步,設(shè)備變得越來(lái)越復(fù)雜化,企業(yè)花費(fèi)在設(shè)備維修上的成本占企業(yè)運(yùn)營(yíng)成本的比例也變得越來(lái)越大。從單臺(tái)設(shè)備的生命周期成本角度來(lái)看,維修成本是全生命周期成本的重要組成部分。因此,優(yōu)化維修成本對(duì)降低企業(yè)運(yùn)營(yíng)成本、提高企業(yè)競(jìng)爭(zhēng)力和全生命周期成本的優(yōu)化有很大貢獻(xiàn)。
目前檢測(cè)到系統(tǒng)的狀態(tài)變得越來(lái)越容易和可信,從而視情維修逐漸成為研究的熱點(diǎn)。視情維修是通過(guò)對(duì)設(shè)備進(jìn)行定期或序貫的或連續(xù)的檢測(cè)來(lái)獲知系統(tǒng)狀態(tài),進(jìn)而安排維修工作以避免產(chǎn)品失效。系統(tǒng)劣化過(guò)程是一個(gè)隨機(jī)過(guò)程,對(duì)于單調(diào)和逐漸劣化的隨機(jī)過(guò)程,用Gamma過(guò)程描述是最合適的。Gamma過(guò)程具有很好的數(shù)學(xué)特性,是一個(gè)具有獨(dú)立、非負(fù)增量的隨機(jī)過(guò)程。Abdel-Hameed提出用Gamma過(guò)程作為描述系統(tǒng)發(fā)生隨機(jī)劣化的適當(dāng)模型,稱為 “Gamma磨損過(guò)程”。Park、Kong和 Park以 Gamma過(guò)程描述系統(tǒng)的劣化過(guò)程,以維修費(fèi)用率最小為目標(biāo),建立了檢測(cè)周期固定的視情維修模型,用解析法求得最優(yōu)預(yù)防維修狀態(tài)閾值。程志君進(jìn)一步考慮維修延遲,以系統(tǒng)的平均費(fèi)用率最低為目標(biāo),聯(lián)合優(yōu)化檢測(cè)間隔期和預(yù)防維修閾值。李玲等將Gamma過(guò)程與幾何過(guò)程相結(jié)合,提出一種加速劣化模型,以系統(tǒng)平均費(fèi)用率最小為目標(biāo),求解最優(yōu)視情維修策略。Huynha et al.考慮系統(tǒng)的劣化和創(chuàng)傷性事件兩種競(jìng)爭(zhēng)失效模式,以維修費(fèi)用率最小為目標(biāo),建立視情維修的定期檢測(cè)/更換模型,得到最佳檢測(cè)間隔期和預(yù)防維修閾值。在目前視情維修的研究中,在以維修成本最低為目標(biāo)時(shí),很少考慮維修時(shí)間且沒(méi)有考慮維修期間內(nèi)的生產(chǎn)損失。
本文針對(duì)連續(xù)劣化單部件系統(tǒng),考慮實(shí)際中普遍采用的定期檢測(cè),建立了以系統(tǒng)平均維修成本率最低為優(yōu)化目標(biāo),以檢測(cè)間隔期和預(yù)防維修閾值為變量的維修優(yōu)化模型。在模型中,假設(shè)預(yù)防維修時(shí)間和故障后維修時(shí)間服從一般分布,考慮檢測(cè)成本、預(yù)防維修成本、故障后維修成本、維修期間的生產(chǎn)損失和維修延遲的停機(jī)損失。
二、模型建立
(一)模型假設(shè)與分析
1.將連續(xù)兩次更新系統(tǒng)至全新?tīng)顟B(tài)的期間定為一個(gè)周期。
2.用隨機(jī)變量 X(t)表示系統(tǒng)在時(shí)刻 t的劣化狀態(tài),若無(wú)維修行為,X(t)是連續(xù)且單調(diào)遞增的。當(dāng)t=0時(shí),X(t)=0,表示系統(tǒng)處于全新工作狀態(tài)。隨機(jī)變量 X(0),X(1)-X(0),… ,X(t)-X(t-1)是非負(fù)、平穩(wěn)和相互獨(dú)立的。
3.對(duì)系統(tǒng)采取視情維修策略,在一個(gè)周期內(nèi)進(jìn)行定期檢測(cè),檢測(cè)間隔期為 T,檢測(cè)時(shí)刻 tk=kT(k=0,1,2…),每次檢測(cè)成本為Ci,檢測(cè)時(shí)間忽略。
4.當(dāng)系統(tǒng)狀態(tài)超過(guò)預(yù)防維修閾值時(shí),進(jìn)行預(yù)防維修;系統(tǒng)發(fā)生劣化故障時(shí),進(jìn)行故障后維修,均修復(fù)如新。其中預(yù)防維修時(shí)間服從均值為βp的一般分布,故障后維修時(shí)間服從均值為βc的一般分布;預(yù)防維修成本為Cp,故障后維修成本為Cc,均不包括生產(chǎn)損失。 其中 Ci≤Cp≤Cc,βp≤βc。
5.系統(tǒng)劣化故障需要檢測(cè)確定,如果發(fā)生劣化故障,直至下次檢測(cè)前系統(tǒng)是失效的,這時(shí)單位時(shí)間內(nèi)失效停機(jī)的生產(chǎn)損失為Cd。
6.系統(tǒng)維修優(yōu)化的目標(biāo)是系統(tǒng)的平均維修成本率最低。
系統(tǒng)存在兩個(gè)狀態(tài)閾值L和M,L是劣化故障閾值,一般由制造商給定,M是預(yù)防維修閾值。對(duì)系統(tǒng)狀態(tài)進(jìn)行定期檢測(cè),在第k個(gè)檢測(cè)時(shí)刻tk檢查到的系統(tǒng)狀態(tài)是 X(tk)。 若 X(tk) 如果預(yù)防維修閾值M設(shè)置得過(guò)低,會(huì)使預(yù)防維修工作增多,可能造成維修過(guò)剩,增加維修成本;設(shè)置的過(guò)高,可能導(dǎo)致維修不足,發(fā)生劣化故障的概率增加,從經(jīng)濟(jì)性和安全性來(lái)看,都是不應(yīng)該發(fā)生的。同樣,檢測(cè)間隔期設(shè)置不當(dāng)也會(huì)造成維修不足或維修過(guò)剩。因此,要使平均維修成本率最低,就要找到最優(yōu)的預(yù)防維修閾值M*、定期檢測(cè)間隔期T*。 圖1 系統(tǒng)周期示意圖 本文用Gamma過(guò)程來(lái)描述兩次維修行為之間的系統(tǒng)劣化過(guò)程。假設(shè)連續(xù)時(shí)間隨機(jī)過(guò)程 {X(t),t≥0}是平穩(wěn)Gamma過(guò)程,則在時(shí)刻t劣化水平的概率密度函數(shù)是形狀參數(shù)為αt、尺度參數(shù)為β的Gamma密度函數(shù)。 Gamma過(guò)程是一個(gè)非減的連續(xù)時(shí)間隨機(jī)過(guò)程,隨α和β的不同,可以描述系統(tǒng)不同的劣化特征。平均劣化率為 α/β,方差為 α/β2。 設(shè)τx表示系統(tǒng)從全新?tīng)顟B(tài)到達(dá)狀態(tài)X的時(shí)間,則τx的分布函數(shù)計(jì)算如公式(2)所示: 其概率密度函數(shù)為: 由更新定理可知:系統(tǒng)平均維修成本率可以看作在一個(gè)周期Γ內(nèi)的維修成本率,因此系統(tǒng)平均維修成本率C(T,M)可表示為公式(4)。 假設(shè)系統(tǒng)在一個(gè)周期內(nèi)檢測(cè)Nk次后更換,則一個(gè)周期的平均長(zhǎng)度E[Γ]和平均維修成本E[C]的計(jì)算如公式(5)、(6)所示。 其中:Pp是系統(tǒng)在一個(gè)周期內(nèi)發(fā)生預(yù)防維修的概率,Pc是系統(tǒng)在一個(gè)周期內(nèi)發(fā)生故障后維修的概率,βp是預(yù)防維修時(shí)間的期望,βc是故障后維修時(shí)間的期望,P{Nk=k}表示系統(tǒng)在第k次檢測(cè)時(shí)更換的概率,E[Nk]是系統(tǒng)在一個(gè)周期內(nèi)檢測(cè)次數(shù)的期望值,E[d]是系統(tǒng)在一個(gè)周期內(nèi)維修延遲的平均時(shí)間。 由公式(4)、(5)和(6)可得到系統(tǒng)平均維修成本率C(T,M),可表示為公式(7): 要找到最優(yōu)的預(yù)防維修閾值M*、定期檢測(cè)間隔期T*,使系統(tǒng)平均維修成本率C(T,M)最小,建立維修優(yōu)化方程如公式(8)所示: 由相關(guān)的數(shù)學(xué)知識(shí)可知,一個(gè)周期內(nèi)檢測(cè)次數(shù)的期望值E[Nk]如公式(9)所示: 其中,檢測(cè)k次的概率P{Nk=k}的計(jì)算如公式(10): 系統(tǒng)更新可能是由預(yù)防維修也可能是由故障后維修引起的,發(fā)生預(yù)防維修的概率Pp和發(fā)生故障后維修的概率 Pc的計(jì)算如公式 (11)、(12)所示: 假設(shè)系統(tǒng)在兩次檢測(cè)之間的時(shí)刻t失效,即(k-1)T<t<kT,則有系統(tǒng)在一個(gè)周期內(nèi)維修延遲的平均時(shí)間E[d],計(jì)算如公式(13): 將公式(9)至公式(13)代入維修優(yōu)化方程(8),可得到系統(tǒng)的平均維修成本率 C(T,M)與決策變量(T,M)之間的關(guān)系。 參數(shù)(α,β)可以通過(guò)對(duì)系統(tǒng)劣化數(shù)據(jù)的分析,利用數(shù)理統(tǒng)計(jì)方法和參數(shù)估計(jì)得到。在此,假設(shè)系統(tǒng)劣化過(guò)程服從參數(shù)是α=1、β=1的Gamma過(guò)程。設(shè)定系統(tǒng)的劣化故障閾值L=10,檢測(cè)費(fèi)用Ci=1,預(yù)防維修成本Cp=10,故障后維修成本Cc=40,維修延遲的單位時(shí)間損失Cd=10,預(yù)防維修時(shí)間的期望βp=0.5,故障后維修時(shí)間的期望 βc=1。 表1 不同檢測(cè)間隔T下的最優(yōu)預(yù)防維修閾值M和平均維修成本率C(T,M) 為使系統(tǒng)的平均維修成本率最低,要找到最優(yōu)維修策略(T*,M*)。 由于函數(shù) C(T,M)的復(fù)雜性,結(jié)合實(shí)際,對(duì)檢測(cè)間隔期T采用離散值,尋求最優(yōu)解。首先根據(jù)經(jīng)驗(yàn)得到T的取值范圍和增加幅度△T;然后考慮預(yù)防維修閾值的約束條件0 將假設(shè)的模型參數(shù)值代入模型,采用上述算法,取最小檢測(cè)間隔為1,最大檢測(cè)間隔為10,考慮實(shí)際情況,置增加幅度△T=1。通過(guò)Matlab編程計(jì)算可得到表1的結(jié)果,由表1可觀察到最優(yōu)的維修策略(T*,M*) =(2,5.9994),此時(shí),C(T*,M*)=2.8273。 本文通過(guò)尋求最佳維修策略,從定量的角度來(lái)優(yōu)化維修成本。對(duì)于連續(xù)劣化單部件系統(tǒng),以Gamma過(guò)程描述其劣化過(guò)程,假設(shè)預(yù)防維修時(shí)間和故障后維修時(shí)間服從一般分布,考慮設(shè)備維修過(guò)程中的檢測(cè)成本、維修成本以及由于維修和維修延遲引起的生產(chǎn)損失,在此基礎(chǔ)上,以系統(tǒng)的平均維修成本率最低為優(yōu)化目標(biāo),以檢測(cè)間隔期和預(yù)防維修閾值為決策變量,建立了維修優(yōu)化模型。算例分析證明了模型的可行性。通過(guò)該模型,可以找到最優(yōu)的檢測(cè)間隔期和預(yù)防維修閾值,使系統(tǒng)的平均維修成本率最低,對(duì)企業(yè)維修成本優(yōu)化的決策有一定的參考作用。
(二)劣化過(guò)程



(三)建立系統(tǒng)平均維修成本率模型

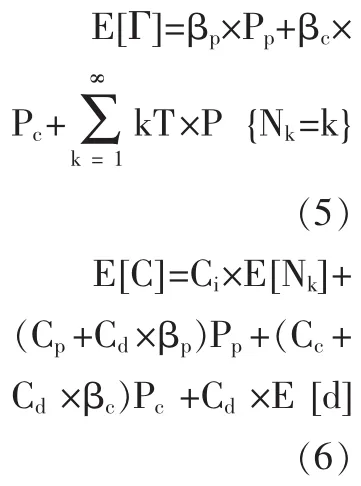

(四)維修優(yōu)化模型

三、模型分析與求解
(一)一個(gè)周期內(nèi)檢測(cè)次數(shù)的期望值
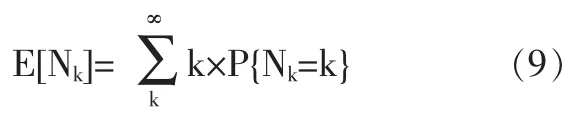


(二)概率 Pp、Pc

(三)維修延遲的平均時(shí)間

四、算例分析

五、結(jié)論
——來(lái)自我國(guó)上市公司的經(jīng)驗(yàn)證據(jù)

