改進的最短路徑矩陣迭代標號法

薛瑞，黃式東，潘虹

（1.信陽師范學院計算機與信息技術學院，信陽　464000；2.信陽師范學院數學與信息科學學院，信陽　464000）

改進的最短路徑矩陣迭代標號法

薛瑞1，黃式東1，潘虹2

（1.信陽師范學院計算機與信息技術學院，信陽464000；2.信陽師范學院數學與信息科學學院，信陽464000）

0　引言

最短路徑（Shortest Paths，SP）是一種典型的網絡優化模型，是解決兩結點之間的最小代價問題。許多優化問題，如設備更新、管道鋪設、線路安排、廠區布局等，都可轉化為網絡最短路徑問題。算法具體的形式包括：確定起點的最短路徑問題、確定終點的最短路徑問題、全局最短路徑問題等。其次還有一些關于最短路徑算法的變形算法相繼被提出：多目標最短路徑算法［1］、K-最短路徑算法［2］、時序最短路徑算法［3］等。

用于解決最短路徑問題的算法被稱做 “最短路徑算法”。到目前為止，解決最短路徑常用的算法有Dijkstra算法［4］和Floyd算法［5］，以及啟發式A*算法［6］等。在這些算法中，Dijkstra算法是典型的單源最短路徑算法。

1　Dijkstra算法概述與分析

Dijkstra算法使用了廣度優先搜索解決非負權有向圖的單源最短路徑問題。所謂單源最短路徑問題是指：已知圖G=（V，E），找出從源結點v1到圖中其他各結點的最短路徑。Dijkstra算法的主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。對Dijkstra算法的改進是近年來國內外學者研究的熱點。例如文獻［7］提出了基于改進蟻群算法的最短路徑問題；文獻 ［8，9］針對多鄰接點與多條最短路徑提出了改進的Dijkstra算法算法；文獻［10］提出了改進的Dijkstra算法在多目標優化中的應用。文獻［11］利用分布式稀疏矩陣對Dijkstra算法進行優化。

1.1Dijkstra算法步驟

如果存在一條從源結點v1到vj的最短路徑（v1，…，vi，vj），vi是vj前面的一結點，那么（v1，…，vi）也必定是從v1到vi的最短路徑。可得從結點v1到達vj的最短距離dist［j］=min｛dist［j］，dist［i］+matrix［i］［j］｝［4］。假設圖G= ＜V，E＞，源結點為v1，P=｛v1｝，dist［j］記錄v1到vj的最短距離，path［j］記錄從v1到vj路徑上的vj前面的一個結點。

①從V-P中選擇使dist［i］值最小的結點vi，將vi加入到P中；

②更新與vi直接相鄰結點vj的dist值。（dist［j］= min｛dist［j］，dist［i］+matrix［i］［j］｝）；

③直到P=V，停止。

1.2Dijkstra算法的不足之處

（1）Dijkstra算法不能解決負權值最短路徑問題，如圖1所示：

圖1　帶負權圖G1

計算從源結點v1到結點v5的最短路徑，用Dijkstra算法得到的結果是v1-v3-v4-v5。主要原因是Dijkstra算法采用的是“標簽算法”，而且對于標記過的點不再進行更新。當v3做為距v1距離最短的點加入邊集U之后，即使負權值可以使得最短值縮短，程序也不會返回v2重新計算最短路徑。

（2）Dijkstra算法需要多次修改結點最短路徑的長度。由于算法遍歷的結點多，特別是對于稠密圖，算法的效率較低。

（3）當從開始點到某個結點之間可能存在多條權重相同的最短路徑時，Dijkstra算法沒有涉及。Dijkstra算法默認為最短路徑上某個結點只有一個前置鄰接點，如圖2所示，從結點v1到結點v7的最短路徑有3條，而用Dijkstra算法只能得到一條最短路徑。

圖2　帶權圖G2

為此，本文針對Dijkstra算法的以上幾點不足，提出了改進的矩陣迭代標號法，有效地解決Dijkstra算法的以上幾點不足之處。

2　矩陣迭代標號法思想步驟

設簡單圖G=＜V，E＞，V=｛v1，v2，…，vn｝，E=｛e1，e2，…，em｝，由于矩陣在計算機中易于存儲和處理，因此可利用矩陣將圖表示在計算機中。稱n階方陣A=（aij）n×n為帶權圖G的距離矩陣。其中：

2.1正圖矩陣迭代算法步驟

令dist（l）［j］表示從源結點v1到達結點vj長度≤l的的最短距離。由于最短路徑是單向無回路的，所以最短路徑最大長度為n-1。為求結點v1到結點vj的最短距離，初始時v1到vj長度為1的最短距離為 a1 j，接著計算v1到vj長度為≤2的最短路徑為，以此類推。若n個點分別以1，2，…，n為編號，迭代過程如下：

①取dist（1）［j］為v1到vj長度為1的最短路徑，則：

③當dist（l）［j］=dist（l-1）［j］，迭代結束，輸出dist（l）［j］=dist ［j］。

定理1：設圖G=＜V，E＞，V=｛v1，v2，…，vn｝，E=｛e1，e2，…，em｝且圖G為簡單帶正權圖，則迭代序列單調遞減收斂于dist［j］，即dist（l）［j］≤dist（l-1）［j］，1≤l≤n-1。

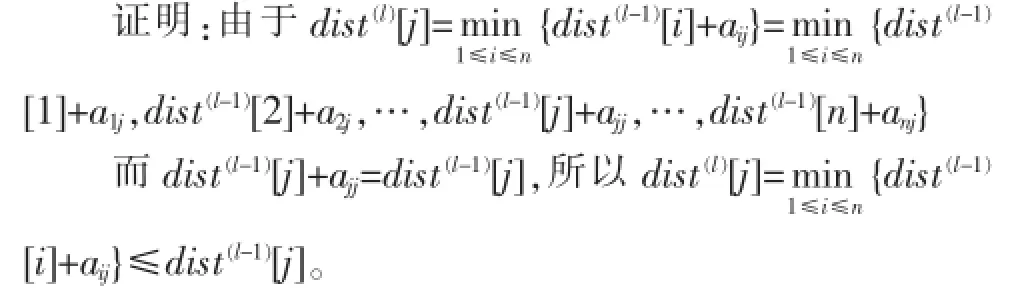
因為單源最短路徑是單向無回路的，故當dist（l）［j］= dist（l-1）［j］時，dist（l）［j］=dist［j］。

定理2：對一個具有n個結點m條邊的有向圖G，若dist（l-1）［j］=dist（l-2）［j］，即第l-1次的迭代結果沒有變化（1≤l≤n-1），則迭代過程可提前結束。

當圖為正權簡單圖時，迭代序列（3）可以快捷地找出最短徑，但是如果存在從源點可達的負回路，則迭代序列因不能收斂而不能求出最短路徑。如圖3所示：

圖3　帶負權圖G3

取v1為源結點，利用迭代序列（3）的迭代結果為：

dist（2）［j］=（0，1，-1，2，0）T，dist（3）［j］=（0，-3，-1，-3，-1）T，dist（4）［j］=（0，-3，-5，-4，-6）T，…，原因是存在負權值回路造成序列不收斂，不能求出最短路徑。

若圖中出現權值為負的邊，如何避免負權值回路是算法的關鍵。目前國內外關于這方面的研究結果非常少，美國數學家Richard Bellman和Lester Ford先后提出一種動態規劃模式算法Bellman-Ford算法［12］，如果存在dist［u］+w（u，v）＜dist［v］的邊，則圖中存在負權值回路，程序返回false。Bellman-Ford算法的限制條件是圖中不能有負權值的回路，而且公式dist［u］+w（u，v）＜dist［v］是判斷回路的必要條件而非充分條件，從而會造成最短路徑漏失。

2.2負權圖矩陣迭代標號法思想步驟

對一個具有n個結點m條邊的簡單負權圖G，首先對n個點分別編號為1，2，…，n，規定源結點編號為1。構造距離矩陣A=（aij）n×n，令dist（l）［j］表示從源結點1到達結點j的長度≤l的的最短距離。設Aj表示從源結點1到點j的最短路徑。U［j］表示從1到j路徑上結點的集合。當j=1時，U［1］=｛v1｝；dist（1）［1］=0；當j≠1時，U［j］=｛v1，vj｝，dist（1）［j］=a1j，j=2，3，…，n。utemp［i］表示臨時最短路徑上節點的集合，utemp［j］的初始值等于U［j］，j=1，2，3，…，n。

①路徑長度l=2，并且路徑長度l＜=n-1；

②現求從v1到vj路徑長度為l的最短路徑，對于頂點Vj，有j=2，j＜=n；

③對于任意的aij，如果vj不屬于U［i］，b［i］=dist（l-l）［i］+aij，utemp［i］=U［i］∪｛vj｝；否則b［i］=無窮大，utemp［i］=U［i］；

④求b［i］數組的最小值min｛b［i］｝；

如果min｛b［i］｝＜dist（l-1）［j］，那么dist（l）［j］=min｛b［i］｝，U［j］=utemp［i］；

否則dist（l）［j］=dist（l-1）［j］，U［j］=U［j］；j=j+1，轉到②；

⑤如果l=n-1，迭代結束，否則l=l+1，轉到②。

2.3仿真實驗分析

仍以圖3中負權圖G3為例，v1，v2，v3，v4，v5分別編號為1，2，…，5，用新算法進行迭代，源結點v1到其余結點的最短路徑及最短路徑權值如表1所示：

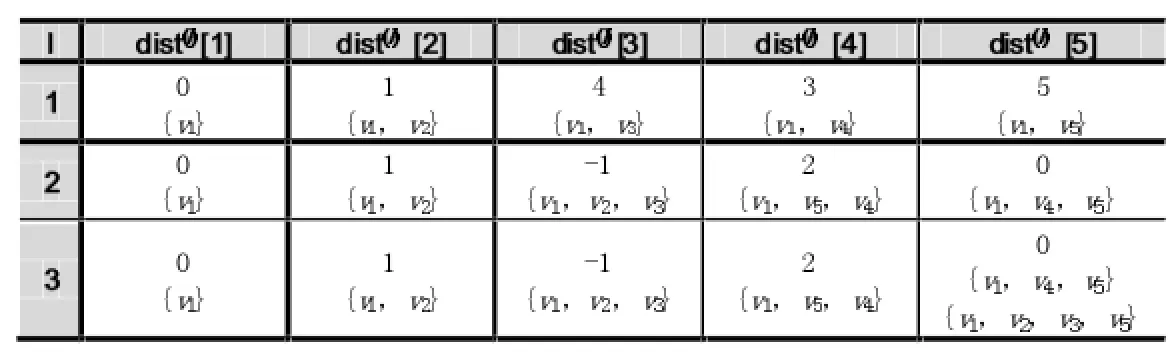
表1　新算法的實驗結果

dist（3）［j］=dist（2）［j］，迭代提前結束。

2.4算法復雜雜度分析

由于改進算法不存在負權值回路，每次迭代最多需要n-1步，一共最多有n-1次迭代，因此時間復雜度為：

f（n）≤（n-1）·（n-1）∈O（n2）

算法的最壞時間復雜度為O（n2）。傳統的Dijkstra算法每次迭代總共需要不超過2（n-1）2+（n-2）步，一共可能有n-1次迭代，所以：

f（n）≤（n-1）·［2（n-1）2+（n-2）］∈O（n3）

改進算法的時間復雜度低于Dijkstra算法，重要的是當圖中存在負權邊或負權值回路時，改進算法仍能得到單向無回路的最短路徑。

3　應用實例

現信陽市政府需要規劃羊山新區的建設工程系統，新區建設主要是由5項子工程構成的：城市交通工程系統、城市供電工程系統、城市綠化工程系統、城市通信工程系統、城市給水工程系統。由于對一項工程的起始條件有著嚴格的限制，所以每項工程的起始時間并不是很容易確定的。分別用 v1，v2，v3，v4，v5代表以上5項子工程的起始時間（單位：月），工程起始的時間差由8個約束條件組成：v2-v1≥0；v5-v1≥1；v2-v5≤1；v3-v1≤5；v4-v1≤4；v3-v4≥1；v3-v5≥3；v4-v5≥3。

根據本文改進算法知道dist［i］+aij≥dist［j］，可以轉化為dist［i］-dist［j］≥-aij，因此可以做以下轉化：若vivj≥-k，則建立一條連接xi到xj的邊，邊權為k；若vsvt≤k，先變形為vt-vs≥-k，再建立一條邊權為k的連接vt到vs的邊。構建矩陣：

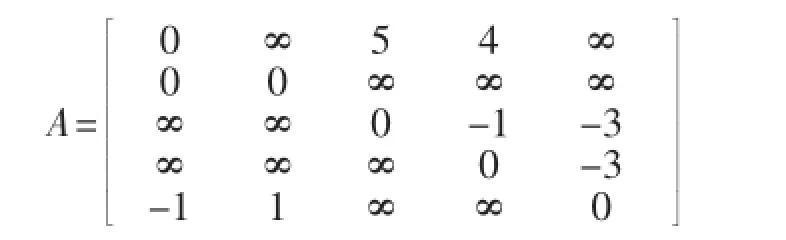
5個點分別編號為1，2，…，5，規定源結點v1=0，迭代結果為：

dist［2］=2，dist［3］=5，dist［4］=4，dist［5］=1。

源結點到個結點的最短路徑為（0，2，5，4，1），即各項工程開工的最短期限。

4　結語

本文針對Dijkstra算法的缺點和不足，提出了改進的矩陣迭代標號算法。改進算法不僅可以有效求解負權值最短路徑問題，而且當從源結點到終點之間可能存在多條權重相同的最短路徑時，改進算法可以得到所有的最短路徑，此外改進算法采取標號的方法，可以有效解決圖中存在負權值回路時的最短路徑問題。由于負權值最短路徑問題廣泛應用于差分約束系統等優化模型中，因此，本文提出的改進算法具有很大的應用價值。另外，在本文的迭代算法中當計算到dist（l）［j］時，dist（l）［1］，dist（l）［2］，…，dist（l）［j-1］都已求得，但卻被束之高閣。因新計算出來的分量要比舊分量更優化，如何用新分量代替舊分量dist（l-1）［1］，dist（l-1）［2］，…，dist（l-1）［j-1］，從而提高算法的收斂速度，這將是后續的研究工作。

［1］Daniel D，Leonardo L，Andres L M.An exact method for the biobjective shortest path problem for the large-scale road networks［J］. European Journal of Operational Research，2015，242：788-797.

［2］Shi N.Constrained shortest path problem［J］.IEEE Transactions on Automations Science and Engineering，2010，7（1）：15-23.

［3］鄧冬梅，王冠楠，朱建等.時序最短路徑算法［J］.計算機科學，2014，41（6）：185-230.

［4］Dijkstra E W.A note on two problems in connetion with graphs［J］.Numberische Mathematik，1959，1（1）：269-271.

［5］Hougardy S.The floyed-warshall algorithm on graphs with negative cycles［J］.Information Processing Letter，2010，4：279-281.

［6］Nicosia G，Oriolo G.An approximate A*algorithm and its application on the SCS problem［J］.Theoretical Computer Science，2003，290 （3）：2021-2029.

［7］宋錦娟，白艷萍.基于改進蟻群算法的最短路徑問題研究及應用［J］.數學的實踐與認識，2013，43（3）：156-164.

［8］王樹西，李安渝.Dijkstra算法中的多鄰接點與多條最短路徑問題［J］.計算機科學，2014，41（6）：217-224.

［9］Wang S X.The improved dijkstra's shortest path algorithm and its application［J］.Procedia Engineering，2012，（29）：1186-1190.

［10］Antonio S N，Andrea R.A dijkstra-like method computing all extreme supported nondominated solutions of the biobjective shortest path problem［J］.Computer&Operations Research，2015（57）：83-94.

［11］Tintor V，Radunovi A J.Distributed dijkstra sparse placement routing algorithm for translucent optical networks［J］.Photonic Network Communication，2009，18（1）：55-64.

［12］Bellman R E.On the routing problem［J］.Quarterly of Applied Mathematics，1958，16（1）：87-90.

Dijkstra Algorithm；Shortest Path Algorithm；Matrix Algorithm

Improved Matrix Iterative Label Algorithm for the Shortest Path Problem

XUE Rui1，HUANG Shi-dong1，PAN Hong2

（1.College of Computer and Information Technology，Xinyang Normal University，Xinyang 464000；2.College of Mathmatics and Information Science，Xinyang Normal University，Xinyang 464000）

1007-1423（2015）26-0003-05

10.3969/j.issn.1007-1423.2015.26.001

薛瑞（1979-），女，碩士，講師，研究方向為智能計算、信息安全

黃式東（1987-），男，河南信陽人，碩士，助教，研究方向為智能計算

潘虹（1980-），女，山東臨沂人，碩士，講師，研究方向為代數拓撲學

2015-09-01

2015-09-10

最短路徑模型是圖論研究中的經典問題，針對傳統的Dijkstra算法的不足，提出改進的矩陣迭代標號法。改進算法不僅可以有效地求解負權值最短路徑問題，而且當兩點間存在多條最短路徑時，改進算法可以同時得到所有的最短路徑。實驗結果表明，改進算法的時間復雜度低于傳統的Dijkstra算法，且算法簡單、易于實現。

Dijkstra算法；最短路徑；矩陣算法

國家自然科學基金青年基金（No.11211400）、河南省自然科學基金研究項目（No.142300410393）

The shortest path model is a classical problem in graph theory，aiming at the shortage of the traditional Dijkstra algorithm，proposes a matrix iterative label algorithm.The Improved algorithm can not only effectively solve the negative weight shortest path problem，and when there are exist multiple shortest paths between two points，the improved algorithm can also get all the shortest paths.Experimental results show that，the improved algorithm has lower time complexity than the traditional Dijkstra algorithm，and the algorithm is simple and easy to implement.