一種基于格的高效簽密方案的分析與設計

鄭曉，王茜，魯龍

（西華大學計算機與軟件工程學院，成都　610039）

一種基于格的高效簽密方案的分析與設計

鄭曉，王茜，魯龍

（西華大學計算機與軟件工程學院，成都610039）

0　引言

保密性、完整性、認證和不可抵賴性是許多加密應用程序的重要要求，如果需要同時實現這些性質，傳統方法是對文件先簽名后加密，1997年Zheng［1］提出一種新的加密原語稱為簽密，同時滿足數字簽名和秘鑰加密兩種功能，成本低于傳統的先簽名后加密的方法。此后，這種簽密體制被廣泛應用于許多應用領域，如電子商務、移動通信和智能卡等。Zheng給出基于離散對數問題的兩個簽密方案，他留下一個通過使用任何公鑰密碼體制，設計其他簽密方案 （如Rivest-Shamir-Adleman RSA［2］）的開放問題，Steinfeld-Zheng［3］和Malone-Lee［4］分別用整數分解和RSA提出簽密方案，后來基于身份的簽密用雙線性對也被提出［5～7］。近年來格密碼迅速發展，相比基于平均情況下依賴于離散對數和因式分解的其他密碼原語，格基密碼的安全性是基于最壞情況下格問題困難性的特點，本文提出的方案在學習錯誤（LWE）假設下，對自適應性選擇密文攻擊具有不可區分性（IND-CCA2），在非齊次小整數解（ISIS）假設下對自適應選擇消息攻擊具有強不可偽造性（sUF-CMA）。

1　預備知識

1.1符號說明

本文中，R表示實數集，Z表示整數集，［n］表示｛1，2，…｝，通過定義f（A）=∑x∈Af（x）把實函數f（·）擴展到可數集A上。用加粗的小寫字母表示列向量，例如x，x的第i個元素表示成xi，矩陣用加粗的大寫字母表示，例如X，X的第i列向量表示成Xi，向量x的長度用歐幾里得范數||x||表示，||x||=maxi||xi||。一個n維格表示成｝是線性獨立向量，B是格基，∧的對偶格定義成∧*=｛x∈Rn: ?y∈∧＜x，y＞∈Z｝，由對稱性，可看到（∧*）*=∧，B*=（B-1）T，所以B*是∧*的一個基。對于任意包含k個線性獨立向量的集合s=｛s1，…，sn｝∈Rn，代表它的格萊姆-施密特正交向量，即=s1對每一個i=2，…n是si的投影，該投影與span（s，…，s）正交，并且‖‖≤‖s‖。

不難得出：∧⊥（A）=q·∧（A）*∧（A）=q·∧⊥（A）*。

格上的高斯分布：對于任意s＞0，定義以向量c為中心，s為參數的高斯分布為：?x∈Rnρs，c（x）=exp（-π

格上離散高斯分布：

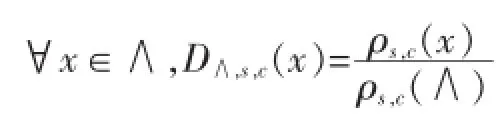
本方案的安全性依賴于LWE和ISIS問題的困難性，為找出這些困難問題，我們需要一些概率分布。

定義兩個分布：

Ψα定義為以0為正態隨機變量均值，標準偏差為在T上模1的分布。定義為以模q為隨機變量在Zq上的離散正態分布，其中X是在Ψα分布中的一個隨機變量。

1.2格上的定義

定義1 LWE判定目標問題LWEq，x：給一整數q和一個在Z上的分布χ，LWE判定問題的目標是：上的As，x分布與上的均勻分布之間用不可忽略的概率加以區分。說明如果LWE問題是困難的，那么As，x的分布集合是偽隨機的。

定義2 標準的LWE問題：從分布As，x中采樣，找到。

命題1［8］表明：對某些模q和高斯錯誤分布χ，用量子算法解決幾個最壞情況下的標準格問題和LWEq，x問題是一樣難的。

命題1給α=α（n）∈（0，1），q=q（n）是一素數，使得，如果存在一個解決的有效算法，那么存在一接近最短獨立向量問題SIVP和判定性的最短距離（GapSVP）問題有效量子算法。

1.3前向采樣函數

2008年，Gentry，Peikert和Vaikuntan-athan［9］定義并創造了前向采樣函數，這里僅給出前向采樣函數的結構，參考文獻［9］前向采樣函數的定義，函數用下面的結果給出［10］。

命題2 給定任意素數q=poly（n）和任意m≥5nl-gq，存在一個概率多項式算法，輸入1n，輸出矩陣A∈和一個滿秩的集合s?∧⊥（A，q），A在上是統計均勻的，并且‖s‖≤L=m2.5。特別地，集合s能被有效地轉化為∧⊥（A）的一個短基T，使得‖‖≤‖‖≤L。

SampleDom（A，s）：B是Zm的標準基，這個算法用在文獻［9］中定義的算法SampleD（B，s，0）從分布中采樣，SampleD（B，s，c）以格基B，參數s，c∈Rm作為輸入，輸出一個統計接近于D∧，s，c的采樣。

SamplePre（T，u）：這個算法以u∈Rn，陷門T作為輸入，輸出和SampleDom算法中一樣的分布e∈Dn，使得Ae=u mod q。

這個函數是無陷門的單向抗碰撞函數，參考文獻［9］表明在均勻輸出u∈Rn的fA逆函數，等價于解決ISIS問題。

1.4GPV簽名方案

H:｛0，1｝*→Rn是一哈希函數，GPV簽名方案包含下面三個算法：

KeyGen（1n）：這個算法運行TrapGen（1n），輸出公鑰A，私鑰T。

Sign（T，m）：給一個消息m簽名，簽名者隨機選一個r←｛0，1｝k，計算δ=SamplePre（T，H（m，r）），m的簽名是（r，δ）。

Verify（A，m，（r，δ））：給出m的簽名（r，δ），當且僅當如果r∈｛0，1｝k，δ∈Dn，fA（β）=H（m，r），驗證者接收這個簽名。

2　簽密的正式模型

2.1一般簽密方案

一般簽密方案包含以下三個算法：

密鑰生成算法KeyGen（1n）：以安全參數n作為輸入，輸出發送者的密鑰對 （pks，sks），接收者的密鑰對（pkr，skr）。

簽密算法Signcrypt（m，sks，pkr）：給出消息m，發送者私鑰sks，接收者公鑰pkr，該算法輸出密文σ。

解簽密算法Unsigncrypt（σ，pks，skr）：給一密文σ，發送者公鑰pks，接收者私鑰skr，該算法要么輸出明文m，要么輸出⊥。這些算法必須滿足簽密的標準一致性約束，即，如果σ=Signcrypt（m，sks，pkr），那么有m=Unsigncrypt（σ，pks，skr）。

2.2安全性表述

簽密方案應滿足保密性與認證性，及與之相對應的能抵抗適應性選擇密文攻擊的不可區分性 （INDCCA2）和適應性選擇消息攻擊的不可偽造性 （EUFCMA）。我們認為強不可偽造性（sUF）比現存不可偽造性更強。

用挑戰者C與敵手A之間的游戲來說明IINDCCA2安全：

Initial：C運行密鑰生成算法生成接收者密鑰對（pkr*，skr*），C把pkr*傳給A，skr*保密。

Phase 1：在解簽密詢問中，A把由發送者密鑰（pks，sks）生成的密文σ發送給C，C運行解簽密預言機并返回m=Unsigncrypt（σ，pks，skr*）。

Challenge：A選兩等長r消息 m0，m1，把它們及（pks*，sks*）發送給C，C隨機從｛0，1｝中選b位，運行簽密預言機并返回密文σ*=Signcrypt（mb，sks*，pkr*），C把σ*發送給A作為一挑戰密文。

Phase 2：A能用不同發送者的密鑰對挑戰密文σ*做一次解簽密查詢。

Guess：A產生一位b'，如果b'=b，贏得游戲。

定義5如果沒有概率t多項式時間，至多qu次解簽密詢問后，敵手A至少有lsc優勢，那么簽密方案是（lsc，t，qu）-IND-CCA2。

用挑戰者C和敵手F之間的游戲來說明sUF-CMA安全：

Initial：C運行密鑰生成算法產生發送者密鑰對（pks*，sks*），C把pks*發送給F，sks*保密。

Attack：在簽名詢問中，F把m，（pkr，skr）發送給C，C運行簽密預言機并返回 σ=signcrypt（m，sks*，pkr），C 把σ發送給F。

Forgery：F選一個接收者密鑰對（pkr*，skr*）并產生一新密文σ*（σ*不是由簽密預言機產生的），如果σ*是有效密文，F贏得游戲。

定義6如果沒有概率t多項式時間，至多qs次簽密詢問后，敵手F至多有lsc優勢，那么簽密方案是（lsc，t，qs）-sUF-CMA。

3　格基簽密方案

我們提出一個格基簽密方案是基于GPV簽名方案的［9］，定義兩個哈希函數：H1:｛0，1｝*→Rn，H2:｛0，1｝*→｛0，1｝l，l是消息的長度。我們方案包含下面三個算法：

KeyGen（1n）：該算法運行TrapGen（1n），產生發送者的公私鑰 （pks，sks）=（As，Ts），和接收者的公私鑰（pkr，skr）=（Ar，Tr）。

Signcrypt（m，sks，pkr）：把一個消息發送給接收者，發送者運行以下步驟：

①r←｛0，1｝*；

②計算δ=SamplePre（Ts，H1（m，r））；

③s∈Znq；

④計算c=m⊕H2（s，δ）；

⑤計算u=ATrs+δ，密文是σ=（c，r，u）。

Unsigncrypt（σ，pks，skr）：當收到一個密文σ=（c，r，u）后，接收者運行以下算法：

①用接收者的私鑰Tr從u中計算出s，δ，

②恢復m=c⊕H2（s，δ）

③當且僅當r∈｛0，1｝k，δ∈Dn，fAs（δ）=H1（m，r）都滿足時接收此密文。

因為（Ar，u=ATrs+δ）是一短向量δ的LWE實例，計算：

TTuu mod q=TTr（ATr+δ）mod q=（ArTr）Ts+TTrs mod q= TTrδ mod q。

因為Tr和δ僅包含小項目，向量TTrδ的每一項遠小于q，因此TTδ mod q=TTrδ所以用（TTr）-1乘 TTrδ得到δ，然后恢復出s。在這個方案中，簽名δ被用作u=ATrs+δ的錯誤項，這個技術是被Gordon，Katz，and Vaikuntanathan［11］創建群簽名提出的。

4　方案的安全性證明

定理1在隨機預言機模型中，如果敵手A在時間t，qu次解簽密詢問和qHi次詢問預言機Hi（i=1，2）后，以不可忽略優勢lsc對抗IND-CCA2安全，那么存在一算法C能在時間t'＜t+（qu+qH）tlwe+qutsig內，以e'≥esc-2的概率解決LWE問題。其中t表示決定（A，u，lwes，δ）是有效LWE實例所需時間，tsig表示決定fAs（δ）=H1（m，r）成立所需時間。

證明：反證法：假設存在一個用不可忽略的概率lsc贏得IND-CCA2游戲的敵手A，創建一個能用概率e'解決LWE問題的算法C，假設C是一個LWE問題的m實例C在IND-CCA2游戲中，敵手A作為一子程序運行，找出s的解來充當敵手A的挑戰者。

Phase 1敵手A執行H1，H2的多項式界定數，并且以自適應的方式解簽密詢問，C分別保留兩個模擬哈希預言機H1和H2的兩個表L1和L2。

H1詢問：對于H1（mi，ri）詢問（1≤i≤qH1），C首先驗證H1的值是否是之前為（mi，ri）輸入定義的值，如果它是，則返回先前定義的值，否則，C隨機選擇h1i∈Rn，把（mi，ri，h1i）插入表L1，返回h1i到A。

H2詢問：對于H2（si，δi）詢問（1≤i≤qH2），C首先驗證H2的值是否是之前為（si，δi）輸入定義的值，如果是，返回先前定義的值，否則C隨機選擇h2i←｛0，1｝l，把（si，δi，h2i）插入表L2，返回h2i到A。

解簽密詢問：如果敵手A發送一個由發送者公私鑰（pks，sks）生成的密文（c，r，u）給一個解簽密詢問，C進行如下：C瀏覽表L2，找（si，δi，h2i），使得u=ATsi+δi以及與之相對應的元素h2i，mi=c⊕h2i使得在表L1中存在一元組（mi，r，hli），如果找不到元組，輸出⊥，C進一步驗證是否fpk（δi）=hli成立，如果成立，mi返回到A，否則，s返回⊥。

Challenge：phase1階段后，A選兩個等長密文m0，m1，把它們以及發送者公私鑰（pks*，sks*）發送給C，C隨機選兩位串r*←｛0，1｝k，c*←｛0，1｝l，讓u*=，C發送挑戰密文σ*=（c*，r*，u*）給A。

Phase 2：A用不同發送者的公私鑰對挑戰密文σ*做解簽密詢問，除非A請求的哈希值，不然它不知道σ*不是一個有效簽密，在那種情況下，LWE的解恰在表L2中，敵手A的模擬觀點是否完美不再重要。

Guess：A產生一結果b'，C檢查（si，δi，h2i）形式的表L2，C驗證是否成立，若成立C輸出LWE解 si，否則C輸出⊥。

我們現在能確定C成功的概率，讓AskH2成為A在模擬期間訪問哈希值的事件，有

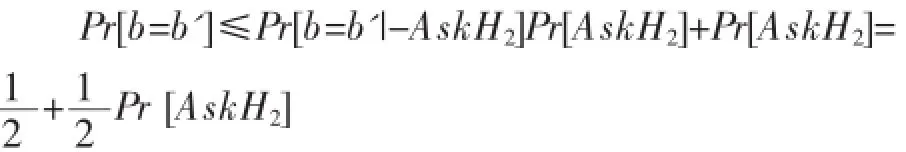
lsc=|2Pr［b=b'］-1|≤Pr［AskH2］。對（si，δi，h2i）在表L2中每一元組恰有一h1i在預言機H1范圍內提供一有效密文，所以有

定理2在隨機預言機模型中，如果敵手F在時間t內，進行qs次簽密詢問和qHi次對預言機Hi（i=1，2）詢問，以不可忽略的優勢lsc對之前方案的sUF-CMA安全，那么存在算法C在時間t'=t內以概率e'≥esc抵抗GPV簽名方案的sUF-CMA安全。

證明：反證法：如果敵手A在上面的方案中能偽造一個簽名，那么在GPV簽名方案中可以偽造一個簽名算法A。

Initial：C給出被攻擊簽名者的公鑰A，讓pks*=A，發送pkr*給F。

Attack：F運行H1、H2多項式界定數，以自適應方式簽密詢問C保留兩個模擬預言機H1、H2的表L1、L2：

H1詢問：對于H1（mi，ri）詢問（1≤i≤qH），C首先驗

1證H1的值是否是之前定義的（mi，ri）輸入的值，若是，則返回之前定義的值，否則，C設置δi=SampleDom（1n）把（mi，ri，δi，fA（δi））放到L1表，返回fA（δi）到A。

H2詢問：對于H2（si，δi）詢問（1≤i≤qH2），C首先驗證H2的值是否是之前定義的（si，δi）輸入的值，若是，則返回之前定義的值，否則，C隨機選擇h2i←｛0，1｝l，把（si，δi，h2i）放到L2表，返回h2i到A。

簽密詢問：如果F對一個由接收者公私鑰（pkr，skr）生成的消息m進行簽密詢問，C用自己的簽名預言機對消息m做簽名詢問得到 （r，δ），然后C把（m，r，δ，fA（δ））放到表L1，最后，C隨機選s∈Zn，計算c=m⊕H2（s，δ），u=pkTrs+δ，（c，r，u）返回到A。

Forgery:

①從u*中用接收者私鑰skr*計算s*，δ*。

②恢復m*=c*⊕H2（s*，δ*）。

③在GPV簽名方案中，輸出（r*，δ*）作為m*的偽造簽名。下面證明正確性：因為σ*=（c*，r*，u*）是有效密文，有fA（δ*）=H1（m*，r*），因此，（r*，δ*）是m*的有效簽名，因為在隨機語言模型下，GPV簽名方案是sUF-CMA安全的，所以我們的方案在隨機預言機模型下也是sUFCMA的，因此有e'≥esc，t'=t。

5　結語

在這篇文章中，我們提出一個在隨機語言機模型下的有效的格基簽密方案，證實我們的方案在LWE假設下是IND-CCA2安全的，在ISIS假設下是sUF-CMA安全的，一次能發送消息長度為L，并且給出Zheng方案的開放問題一個新的解。

［1］Zheng Y.Digital Signcryption or How to Achieve Cost（Signature&Encryption）Cost（Signature）+Cost（Encryption）.In Proceedings Advances in Cryptology-CRYPTO'97，LNCS 1294.Springer-Verlag:Santa Barbara，California，USA，1997：165～179

［2］Rivest RL，Shamir A，Adlema L.A Method for Obtaining Digital Signatures and Public Key Cryptosystems.Communications of the ACM 1978，21（2）:120～126

［3］Steinfeld R，Zheng Y.A Signcryption Scheme Based on Integer Factorization.In Proceedings Information Security ISW 2000，LNCS 1975.Springer-Verlag:Wollongong，NSW，Australia，2000：308～322

［4］Malone-Lee J，Mao W.Two Birds One Stone:Signcryption Using，RSA.In Proceedings Topics in Cryptology-CT-RSA，2003，LNCS 2612.Springer-Verlag:San Francisco，CA，USA，2003：211～225

［5］Boyen X.Multipurpose Identity-Based Signcryption:a Swiss Army Knife for Identity-Based Cryptography.In Proceedings Advances in Cryptology-CRYPTO 2003，LNCS 2729.Springer-Verlag:Santa Barbara，California，USA，2003：383～399

［6］Chen L，Malone-Lee J.Improved Identity-Based Signcryption.In Proceedings Public Key Cryptography-PKC 2005，LNCS 3386. Springer-Verlag:Les Diablerets，Switzerland，2005：362～379

［7］Barreto PSLM，Libert B，McCullagh N，Quisquater J.J.Efficient and Provably-Secure Identity-Based Signatures and Signcryption from Bilinear Maps.In Proceedings Advances in Cryptology-ASIACRYPT，LNCS 3788，Springer-Verlag:Chennai，India，2005：512～523

［8］Regev O.On lattices，Learning with Errors，Random Linear Codes，and Cryptography.Journal of the ACM 2009，56（6），Article

［9］Regev O.on lattice，Learning with Errors，Random Linear Codes.and Cryptography.Journal of the ACM 2009，56（6）Article34

［10］Ajtai M.Generating Hard Instances of the Short Basis Problem.In Proceedings Automata，Languages and Programming-ICALP 1999，LNCS 1644.Springer-Verlag:Prague，Czech Republic，1999：1～9

［11］Gordon SD，Katz J，Vaikuntanathan V.A Group Signature Scheme from Lattice Assumptions.In Proceedings Advances in Cryptology-ASIACRYPT 2010，LNCS 6477.Springer-Verlag:Singapore，2010：395～412

Lattice；Random Oracle；Signcryption

Analysis and Design of an Efficient Lattice-Based Signcryption Scheme

ZHENG Xiao，WANG Qian，LU Long
（Institute of Computer Software Engineering,Xihua University，Chengdu 610039）

1007-1423（2015）08-0003-05

10.3969/j.issn.1007-1423.2015.08.001

鄭曉（1984-），女，山東德州人，碩士研究生，研究方向為計算機技術

王茜（1990-），女，湖北宜昌人，碩士研究生，研究方向為計算機技術

魯龍（1989-），男，山東臨沂人，碩士研究生，研究方向為計算機軟件與理論

2015-01-29

2015-03-06

簽密是同時執行數字簽名和公共密鑰加密兩種功能的一個加密原語，所需成本比通過傳統的先簽名后加密的方法低。設計一個一次發送長度為L消息的高效簽密方案。并證明，該方案在錯誤學習假設下具有適應性選擇密文攻擊不可區分性（IND-CCA2），在非均勻小整數解假設下具有適應性選擇消息攻擊強不可偽造性（SUF-CMA）。與基于數論假設方案相比，該方案具有密鑰空間較大，但效率更高。

格；隨機預言機；簽密

Signcryption is a cryptographic primitive that performs simultaneously both the functions of digital signature and public-key encryption,at a cost significantly lower than that required by the traditional signature-then-encryption approach.Designs an efficient signcryption scheme that can send a message of length L one time.Proves that the proposed scheme has the indistinguishability against adaptive chosen ciphertext attacks under the learning with errors assumption and strong unforgeability against adaptive chosen messages attacks under the inhomogeneous small integer solution assumption inthe random oracle model.Compared with the schemes based on factoring or discrete log,the public and secret keys of the scheme are large,but it requires only linear operation on small integers.