淺談圖像融合算法

張鋮方，閆皓輝

（西華大學無線電管理技術研究中心，成都　610039）

淺談圖像融合算法

張鋮方，閆皓輝

（西華大學無線電管理技術研究中心，成都610039）

0　引言

隨著圖像傳感器技術的不斷發展，所采集到的多模態圖像具有更豐富的信息，圖像融合就成為圖像處理領域重要的研究內容之一。圖像融合是利用給定方法將同一目標場景的兩幅圖像變成一幅包含豐富信息的圖像，融合后的圖像包含了原始圖像的所有信息。由于像素級融合具有融合過程簡單，實現方便的優點，已成為目前國內外的主要研究焦點。圖像融合技術應用非常廣泛，目前，已廣泛應用于醫學、遙感等領域。本文首先簡單地介紹圖像融合系統和結構；其次闡述了近年來幾種主流的融合方法，著重介紹了基于聯合稀疏模型的融合方法；最后，簡述幾種常用的圖像融合評價指標。

1　圖像融合簡介

1.1圖像融合系統

以往的傳感器所獲取圖像信息是有限的，這樣的話很難滿足當前的要求。隨著傳感器種類的增多，所獲得的圖像信息也變得多樣，并且信息的內容更加復雜。圖像融合技術可將這些復雜的信息整合在一起，并有利于人們對圖像目標進行進一步的識別、檢測。圖像融合系統如圖1所示。

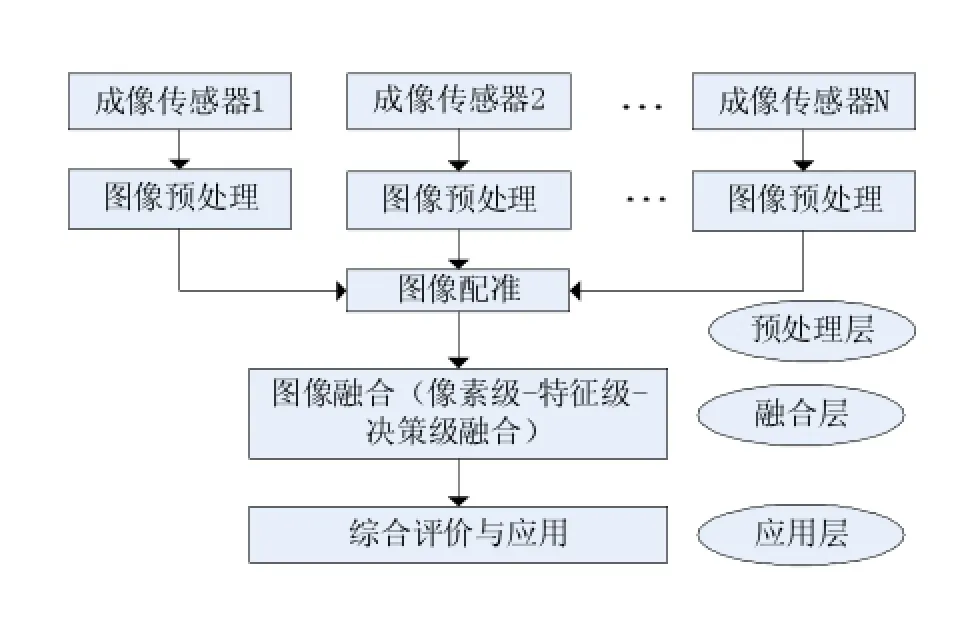
圖1　圖像融合系統

1.2圖像融合分層結構

圖像融合的結構一般分為三個層次：像素級融合、特征級融合、決策級融合，如圖2所示。像素級融合是最簡單也是最直接的一種融合方法，即直接將從圖像傳感器獲得的圖像數據進行處理而獲得融合圖像，其融合算法有PCA和小波分解融合法等；特征級融合首先獲得圖像的不同特征，然后利用某些算法融合圖像的這些特征；決策級融合是最高級的融合，融合方法有基于貝葉斯法的決策級融合等。

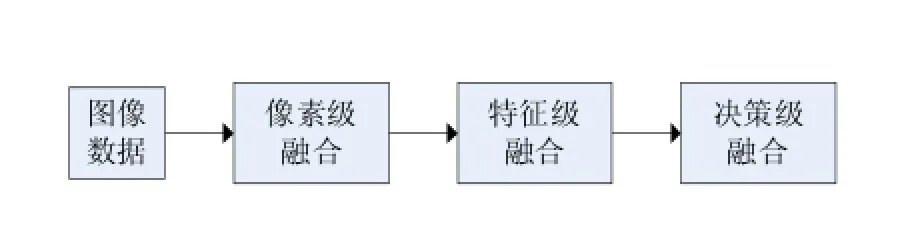
圖2　圖像融合的三層結構

2　融合方法

像素級融合是目前圖像融合領域研究的熱點，并且保存了較完全的原始圖像數據。因此，本文主要介紹像素級圖像融合的一些方法。

自圖像融合技術提出以來,許多像素級的融合方法被提出，主要分為空間域算法和變換域算法。下面主要介紹這兩種常用的融合方法。

2.1空間域融合算法

（1）基于IHS空間的圖像融合算法［1］

基于IHS空間的圖像融合是像素級融合中最常用的方法，也是最早提出的一種利用偽彩色的融合方法，其基本思想是利用IHS變換快速的特點將待融合圖像先進行IHS變換，然后使用特定的規則進行融合，最后使用IHS逆變換變成RGB圖像。具體融合框圖如圖3所示。

圖3　基于HIS變換的圖像融合框圖

從RGB變換到IHS的公式為：

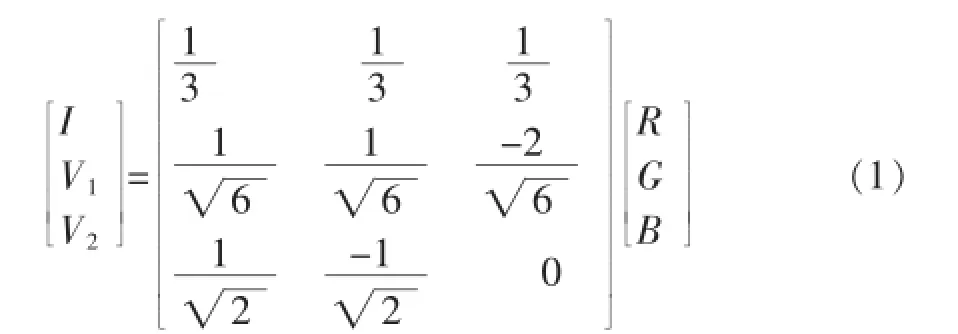
IHS反變換公式如下：

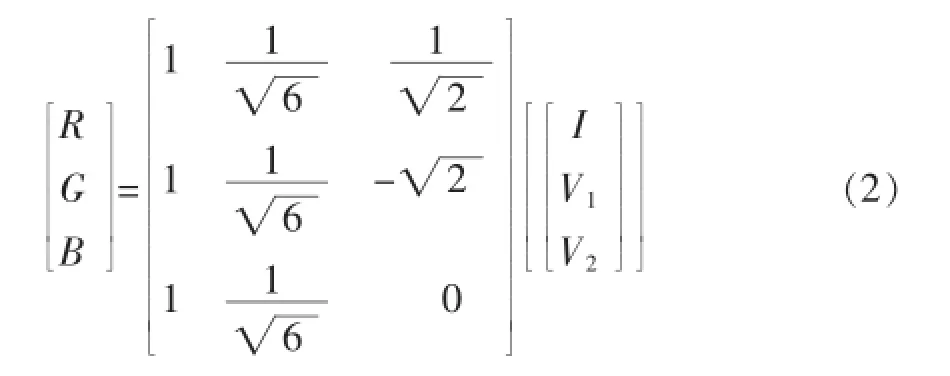
（2）加權平均融合方法［2］

加權平均法是最簡單且執行效率最高的融合方法?；舅枷胧峭ㄟ^設定各自的比重系數，將兩幅圖像的不同信息進行線性相加。待融合圖像記為A和B，融合圖像為F，則具體的融合過程用公式表示為：

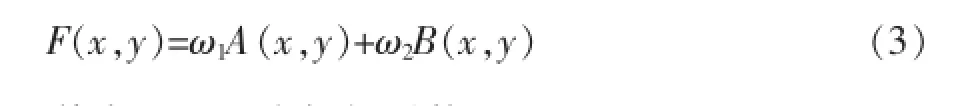
其中，ω1，ω2為加權系數，ω1+ω2=1。

雖然加權平均法執行效率高，但在對于多模態圖像，該方法使得圖像中的輪廓變模糊，融合效果變得很差。主成量分析方法（PCA）是常用的一種加權平均融合方法，不僅通過降維使得圖像融合過程的計算量減少，而且在一定程度上抑制噪聲。

2.2變換域融合算法

基于變換域的圖像融合方法的基本思想：首先對兩幅輸入的多模態圖像進行相應的變換（如小波變換、NSCT等），并得到分解后的系數；然后將系數按一定的融合規則進行融合；最后對融合后的系數使用與第一步相對應的逆變換重構，進而獲得融合后的圖像?；诙喑叨茸儞Q的融合算法框圖如圖4所示。

（1）基于金字塔分解的圖像融合［3］

金字塔分解包括:拉普拉斯金字塔變換、形態學金字塔變換等。Burt等人首次提出基于拉普拉斯塔式的圖像融合?；诮鹱炙儞Q的融合方法的基本思想是利用塔式分解方式獲得原始圖像在不同空間分辨率上的特征，并用系數表示。這種方式相比于空間域，更能突出圖像的豐富信息。也就能夠獲得更優的融合效果。經過塔式分解后，圖像各層間的數據存在大量的冗余信息。雖然融合效果優于空間域，但是這些冗余信息會導致圖像的主觀識別能力減弱。而且，當待融合圖像在損失了較多的高頻信息的情況下，重構時易造成邊緣和輪廓模糊，影響判別。

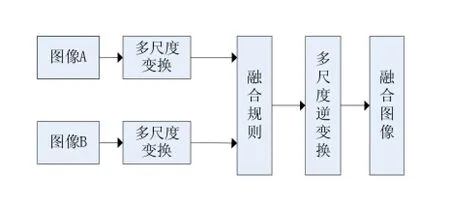
圖4　基于多尺度分解的圖像融合算法框圖

（2）基于小波變換的圖像融合［4］

相比于金字塔分解，小波變換解決了塔式分解中存在的冗余信息的缺點，同時提取圖像低頻信息和高頻信息，在理論上比傳統的拉普拉斯金字塔融合方法具有更好的效果。Ranchi等人首次將小波變換應用圖像融合中并取得較好的融合效果。與基于塔式分解的融合方法相似，基于小波變換的圖像融合算法首先通過小波變換將原始圖像分解為具有不同空間分辨率的子圖像；然后對低頻和高頻系數分別使用不同的融合規則；將融合后的系數經過小波逆變換獲得融合后的圖像。具體算法框圖如圖5。

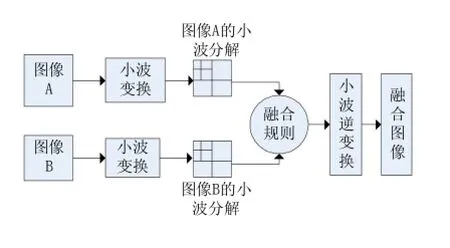
圖5　基于小波變換的圖像融合算法框圖

（2）基于NSCT的圖像融合［5］

NSCT是Contourlet變換的一種變形，NSCT可以較好地提取圖像邊緣輪廓信息。Jingjing Wang等人利用NSCT的平移不變性特點，將NSCT和PCNN結合在一起并應用到圖像融合。基于NSCT的圖像融合的基本思想和基于小波變換的圖像融合相似，首先通過NSCT分解原始圖像；然后對低頻和高頻系數分別使用不同的融合規則；將融合后的系數經過NSCT逆變換獲得融合后的圖像?；贜SCT的圖像融合方法框圖如圖6所示。

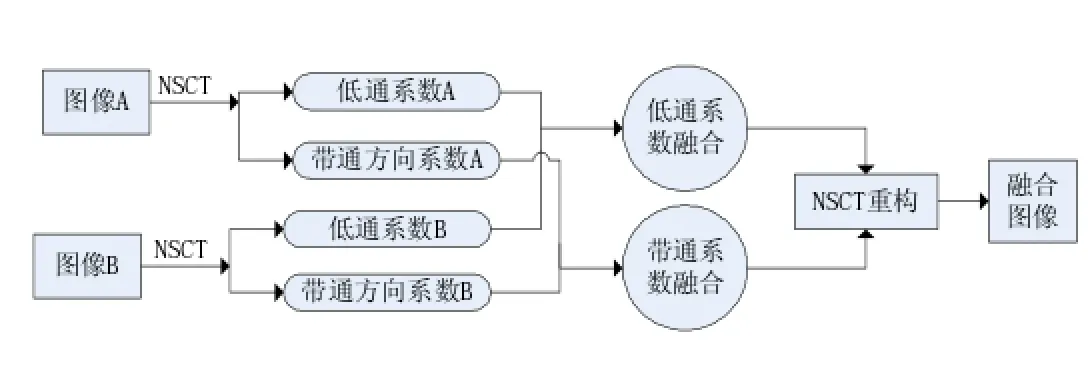
圖6　基于NSCT的圖像融合算法框圖

（3）基于稀疏表示的圖像融合［6］

自從2006年壓縮感知理論被提出，信號的稀疏表示理論已經引起了廣大研究者的興趣，并且將該理論應用到圖像處理的各個領域（去噪、融合、超分辨）。李樹濤首次提出基于稀疏表示的圖像融合算法，并將該方法應用到多聚焦圖像的融合。在文獻［6］中是首先將兩幅原始圖像通過窗口滑塊技術變成圖像塊；然后利用過完備的DCT（Discrete cosine transformation）字典，使用OMP算法對所得的圖像塊進行稀疏分解，得到相對應的稀疏系數；其次選取L1范數大作為融合規則，獲得融合系數；最后將獲得的融合系數和DCT字典作用于OMP重建出融合圖像?；谙∈璞硎镜膱D像融合框圖如圖7所示。

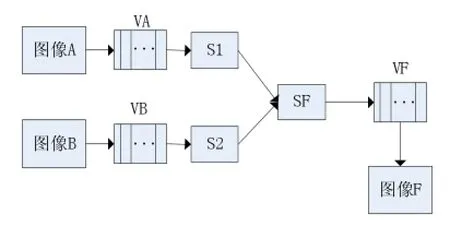
圖7　基于稀疏表示的圖像融合算法框圖

雖然基于稀疏表示的圖像融合效果優于基于多尺度變換的圖像融合方法，但是該方法沒有考慮到待融合圖像之間的聯系，而且計算效率不高，與此同時，文獻［6］只是用DCT作為字典，并沒有使用學習的策略獲得更加冗余的字典。

（4）基于聯合稀疏表示的圖像融合［8］

針對于單純的基于稀疏表示的圖像融合沒有考慮輸入圖像之間的聯系，文獻［9］在分布式壓縮感知理論（DCS）的基礎上提出三種不同的聯合稀疏模型，即JSM-1，JSM-2和JSM-3。目前，JSM-1以其簡單的理論思路，已成為目前基于聯合稀疏模型的圖像融合算法中最常用的一種模型。在JSM-1模型中，圖像信號包括共同分量和特征分量，并且是兩者之和。2011年Haitao Yin等人首次提出基于聯合稀疏表示的圖像融合，文獻［8］中采取的策略是：首先提取圖像的公共特征和各自特征，并采用K-SVD算法［10］訓練字典，然后將JSM應用到紅外、醫學、毫米波等的圖像融合，由于考慮了輸入的兩幅圖像間的相似性，融合效果優于基于稀疏表示的圖像融合?；诼摵舷∈璞硎镜膱D像融合的框圖如圖8所示。

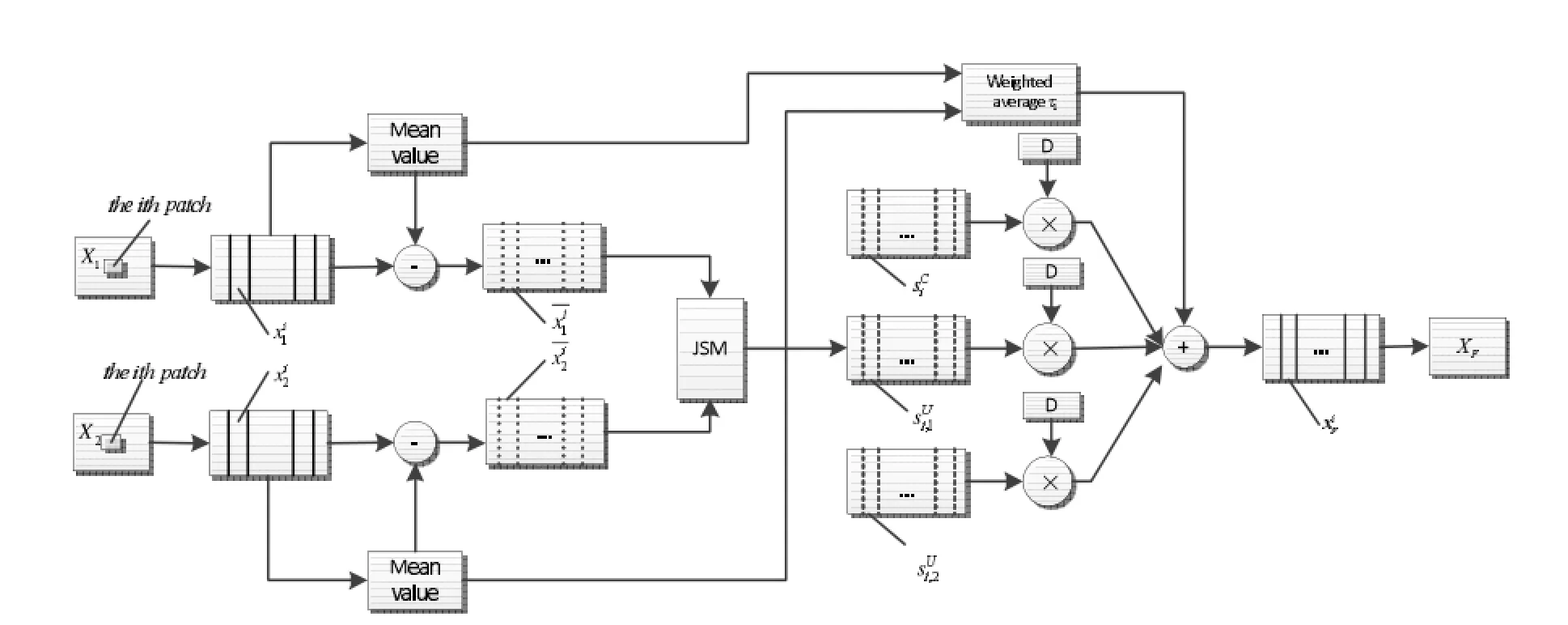
圖8　基于聯合稀疏模型的圖像融合算法框圖

3　融合規則

不管是基于空間域還是基于變換域的圖像融合，都涉及融合規則的選擇問題?；诳臻g域的融合常用的融合規則是取大。這里主要關注基于稀疏表示和聯合稀疏模型的系數融合規則。文獻［6］給出了基于稀疏表示的圖像融合的融合規則，文獻［7］和文獻［10］分別給出了兩種不同的基于聯合稀疏模型的圖像融合的融合準則，如下所示：

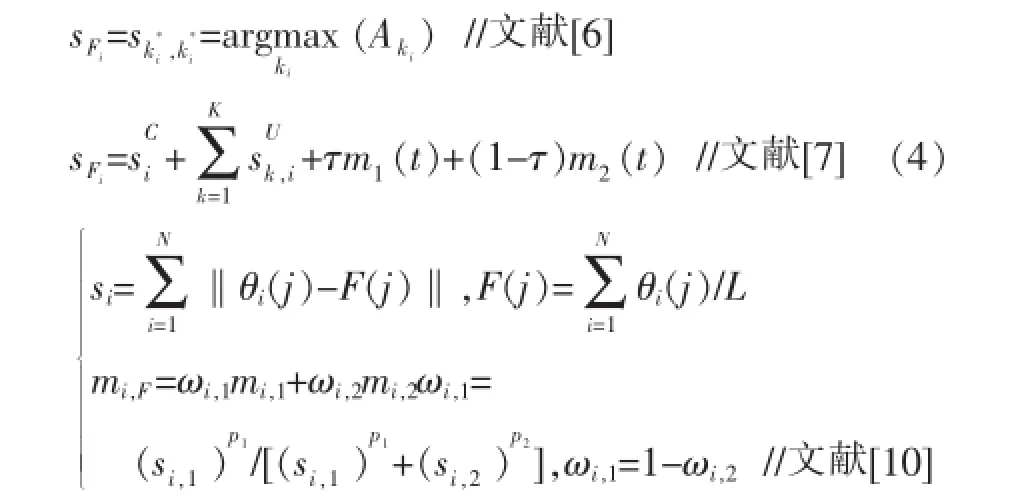
文獻［6］中，Ak=‖sk‖1，sk是第k個源圖像第i列稀iii疏系數，s是融合圖像第i列稀疏系數。文獻［7］中，和ki分別為稀疏表示系數矩陣sC和的第i列，sF為融i合圖像的稀疏系數矩陣sF的第i列。τ=1/1+exp｛-β（‖（）‖2-‖（x2）‖2）｝），（β＞0））。=x1-m1，x2=x2-m2，m1，m2表示每塊的均值。文獻 ［10］中，L表示源圖像的所有塊中局部強度值的個數，p1，p2是對應的調整不同源圖像重要性的權重指數。

4　融合評估方法

融合效果的評價大致分為兩種，即主觀感覺評估和客觀評估。目前以客觀評估為主，文中同樣主要介紹融合的客觀評價?？陀^評價指標有許多，常用的有信息熵、互信息、平均梯度、Qabf等。下面簡單介紹幾種常用的評價指標

（1）互信息［11］

互信息是信息論的概念，延伸到圖像領域，表示兩幅圖像灰度分布信息的相關性。假設待融合的兩幅圖像為A、B，經過融合后的圖像為F，那么，互信息為：

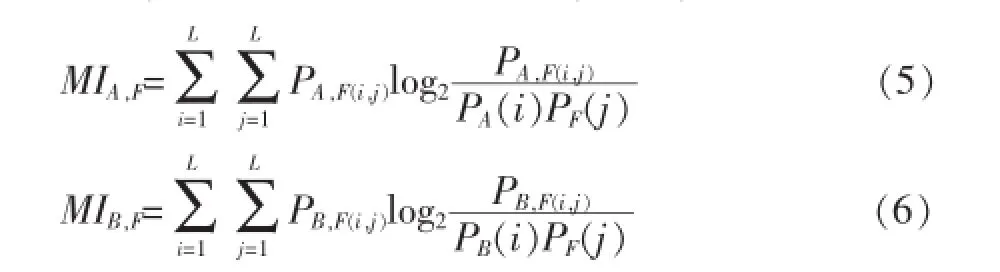
其中PA，F（i，j）和PB，F（i，j）分別為兩組圖像的聯合灰度分布，L是圖像總的灰度級數。

由式（5）和式（6）可以得出，融合圖像與原始兩幅圖像的互信息為：

式（7）表明，互信息值越大，圖像F從源圖像A和B中獲得的信息越多，表明融合后的圖像內容越豐富，進而融合的效果越好。

（2）邊緣信息保留值［12］

A、B為源圖像，F為融合圖像，則Qabf的計算公式如下：

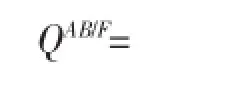
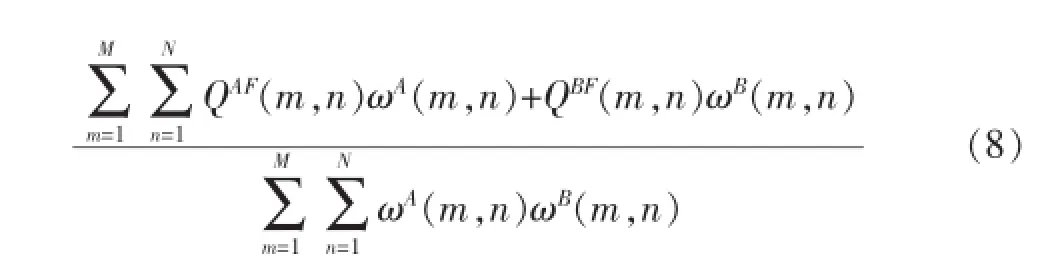
QAF和QBF分別為圖像A、圖像B和融合圖像F的邊緣信息保留值。ωA和ωB為權值。M和N為圖像的高與寬。

（3）Piella融合質量標準［13］

Piella和Heijmans提出了一種新的圖像融合質量評價標準，該標準主要基于通用圖像融合指數（UIQI），以更精細的加權平均方式度量了融合圖像的UIQI。

PFQM體系包括了圖像融合質量指數（Image Fusion Quality Index，IFQI），加權融合質量指數（Weighted Fusion Quality Index，WFQI）和邊緣相關融合質量指數（Edge-dependent Fusion Quality Index，EFQI）。圖像融合質量指數（IFQI）定義為：

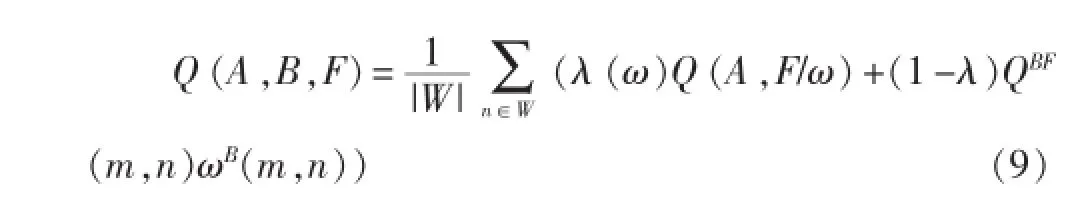
其中ω表示各窗口，λ（ω）為對應窗口間的權值：

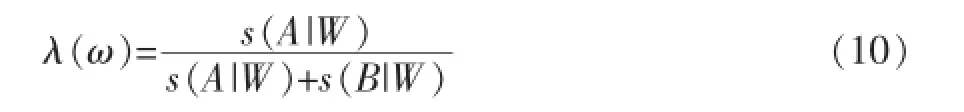
s（A|W）和s（B|W）分別為源圖像A和B在窗口ω中的顯著性度量，一般用對比度、尖銳度或熵等數值表示。上式認為圖像各個局部塊的重要性是相同的，因此做了算術平均處理。但實際上圖像各個部分的顯著性是不一樣的，顯著性高的部分對應了更加重要的信息，因此評價融合質量時應該將圖像各部分按重要性區分對待?；诖怂枷?，Piella定義了各窗口的總體顯著性：

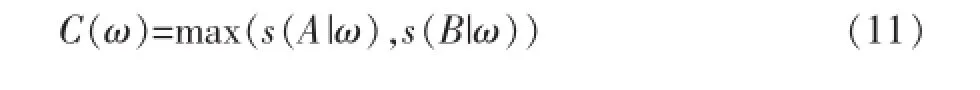
基于圖像各局部塊的總體顯著性，加權融合質量指數（WFQI）的定義為：

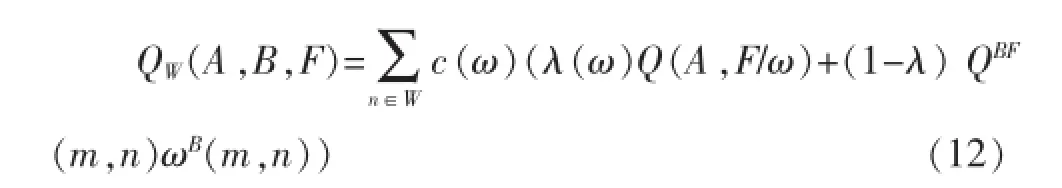
其中，c（ω）為權重，衡量了個窗口的重要性，其形式如下：

為了突出邊緣圖像對于人類視覺系統的重要性，Piella進一步提出了邊緣相關融合質量指數（EFQI）：

QE（A，B，F）=QW（A，B，F）1-α.QW（A'，B'，F'）α（14）

其中A'，B'，F'分別為圖像A，B，F的邊緣圖像，α為控制參數，決定了原圖像和邊緣圖像的WFQI的比例。

5　結語

由于分布式壓縮感知理論和聯合稀疏表示的不斷研究，基于聯合稀疏模型的圖像融合已經成為逐步成為圖像融合領域的主流，目前，該基于該方法的圖像融合已應用到醫學、軍事等領域，并取得了一定的效果。但是，還存在一些的難題：

（1）目前的圖像融合主要是以像素級為主，很少涉及到更高一層的融合，由于像素級融合面向的是圖像的像素，目前所研究的圖像像素比較少，如果將目前的像素級融合策略應用到高分辨率圖像的融合，那么，就會造成計算開銷大、效率低等問題。

（2）圖像融合的前提需要進行許多預處理操作，如，去噪、配準等。但是，目前所針對的圖像，絕大部分是經過完全配準后的圖像。對于有噪聲或者沒有完全配準的圖像融合的研究，很少有學者涉及。

（3）當今的圖像傳感器種類多種多樣，所獲取的圖像蘊含的信息也隨之增加。2D圖像已不能滿足醫學、軍事等方面的需求，3D圖像信息的融合逐漸成為信息融合的研究熱點。但目前關于3D圖像融合的方法很少，并且3D圖像融合還要考慮時間維度，這樣致使融合計算時間更長，開銷更大。

針對以上所提的3個問題，本文提出三個相應的解決辦法：

（1）對于效率低的問題，將多尺度變換和聯合稀疏表示結合應用到圖像融合，首先將圖像進行多尺度變換；然后利用所學的多尺度字典對變換后的多尺度圖像進行系數分解；接著將所得到的稀疏系數通過融合規則得到融合獲得系數；最后利用多尺度反變換重構出融合圖像。

（2）對于去噪和配準的問題，將基于稀疏表示的圖像去噪和基于膜計算的圖像配準算法引入到圖像預處理階段。

（3）對于開銷大的問題，可以采用并行處理，將并行計算的思想引入到圖像融合，減少計算時長。

［1］Krista Amolins，Yun Zhang.Peter Dare.Wavelet Based Image Fusion Techniques—An Introduction，Review and Comparison［C］.ISPRS Jouenal of Photogrammetry&Remote Sensing，2007：249-263.

［2］Chavez，S.，Sides，C.，Anderson，A..Comparison of Three Different Methods to Merge Multiresolution and Multispectral Data:Landsat TM and SPOT Panchromatic［J］.Photogrammetric Engineering and Remote Sensing，1991，57（3）：295-303.

［3］韓瀟，彭力.基于改進拉普拉斯金字塔的融合方法［J］.自動化與儀器儀表，2014，5，191-194.

［4］樊華，等.改進的IHS變換和小波變換相結合的圖像融合［J］.CT理論與應用研究，2014，23（5），761-770.

［5］陳木生，蔡植善.基于NSCT的紅外與可見光圖像融合方法研究［J］.激光與光電子學進展，2015，52（6），114-119.

［6］Bin Yang，Shutao Li.Multifocus Image Fusion and Restoration With Sparse Representation［J］.IEEE Transactions on Instrumentation and Measurement.2010，59（4）:884-892.

［7］Yin H，Li S.Multimodal Image Fusion with Joint Sparsity Model［J］.Optical Engineering，2011，50（6）:067007-067007-10.

［8］Duarte M F，et al.Distributed Compressed Sensing of Jointly Sparse Signals［C］.Asilomar Conf.Signals，Sys，Comput.2006:1537:1541.

［9］M.Aharon，M.Elad，A.Bruckstein.K-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［J］.IEEE Trans.Signal Process，2006，54（11）：4311-4322.

［10］Bin Yang，Shutao L.Visual Attention Guided Image Fusion with Sparse Representation［J］.Optik.2014，125（17）:4881-4888.

［11］G.H.Qu，D.L.Zhang，P.F.Yan.Information Measure for Performance of Image Fusion［J］.Electron.Lett.2002，38（7）:313-315.

［12］C.S.Xydeas.Objective Image Fusion Performance Measure［J］.Electron.Lett，2000，36（4）:308-309.

［13］G.Piella，H.Heijmans.A New Quality Metric for Image Fusion［C］.Proc.of Int.Conf.on Image Processing，Barcelona，Spain，2003:173-176.

Image Fusion；Distributed Compressed Sense；Joint Sparse Model

Review of Image Fusion Algorithm

ZHANG Cheng-fang，YAN Hao-hui

（Center for Radio Administration&Technology Development，Chengdu 610039）

1007-1423（2015）32-0061-06

10.3969/j.issn.1007-1423.2015.32.015

張鋮方（1990-），男，河南濟源人，碩士，讀碩士研究生，研究方向為圖像處理與模式識別

2015-10-09

2015-11-09

圖像融合是信息融合的一個熱點。隨著分布式壓縮感知理論的發展，聯合稀疏表示成為分布式壓縮感知中的一個重要的研究內容。在闡述主流的圖像融合技術的同時，著重介紹聯合稀疏表示在圖像融合中的應用，并簡單地介紹幾種圖像融合評估方法。最后，對未來的圖像融合發展提出新的思路。

圖像融合；分布式壓縮感知；聯合稀疏模型

四川省教育廳重點項目（No.14ZA0118）

閆皓輝（1992-），女，山西長治人，碩士，在讀碩士研究生，研究方向為智能信息處理

Image fusion is a hot topic in the information fusion.With the development of the theory of distributed compressed sensing(DCS),joint sparse representation is becoming an important research content during the field of distributed compression.Elaborates mainstream image fusion technology,focuses on joint sparse representation in image fusion applications at the same time.What's more,introduces several image fusion evaluation methods.Finally,proposes new ideas for the future development of image fusion propose.