基于相似度對系統循環碼參數的盲識別

王蘭勛，熊政達，佟婧麗

(河北大學 電子信息工程學院，河北 保定 071002)

基于相似度對系統循環碼參數的盲識別

王蘭勛，熊政達，佟婧麗

(河北大學 電子信息工程學院，河北 保定 071002)

針對系統循環碼參數的盲識別問題，提出了一種基于數據挖掘中相似性度量函數的方法。首先，在不同的先驗知識下，利用實際序列與隨機序列的碼重分布相似度差異最大的特性識別碼長和起始點，在此基礎上，通過優化傳統的矩陣化簡，由碼字多項式與生成多項式的關系設定判定門限T的方式求解生成矩陣，實現了對系統循環碼的盲識別。仿真結果表明，該算法在誤碼率為0.01的條件下識別效果較好。

系統循環碼； 盲識別； 碼重相似度； 生成矩陣

信道編碼的盲識別是在未知編碼信息的條件下僅根據接收到的數據快速識別編碼結構，在信息截獲、非協作通信、軟件無線電和智能通信等領域具有廣泛的應用，對該技術進行研究具有重要的價值[1-3]。

循環碼被廣泛應用于通信、軍事等領域中，但目前，據現在公開發表的文獻來看，大部分文獻集中在卷積碼的盲識別上，較少研究循環碼的盲識別。文獻[4]根據實際碼重與均勻碼重之間的距離估計碼長；文獻[5]根據比特率檢測法識別碼長和起始點，二者均適用低誤碼率的環境；文獻[6]根據矩陣秩信息熵識別碼長及碼重信息熵識別起始點，高誤碼條件下識別較好；文獻[7]根據歐幾里德算法得到最大公因式，完成對碼長及生成多項式的識別；文獻[8]根據碼根信息差熵和碼根統計識別碼長和生成多項式，二者雖容錯性較好，但均只適用于本原BCH碼的識別；文獻[9]根據秩函數和碼根特征實現循環碼的盲識別，雖適用于較高的誤碼環境，但運算量會增加；文獻[10]根據碼重分布不均勻的特性識別碼長和起始點，雖運算量較小，但容錯性一般；文獻[11]根據碼重分布概率方差識別碼長，計算碼多項式的公約式求解生成矩陣，無復雜計算，需已知起始點。

上述的識別算法，針對性較強、計算量大或容錯性一般，針對這些不足，本文提出了一種基于數據挖掘中相似度的方法進行識別，本算法無復雜計算、適用于一般循環碼且容錯性較好。首先，在不同的先驗知識下，利用碼重相似性度量函數識別碼長和起始點，進而對傳統矩陣進行優化來獲得生成矩陣，并設置判決門限進行驗證。理論分析并與其他算法進行比較，仿真結果表明，該算法在不需要大量數據截取的條件下，在高誤碼率為0.01時能夠識別碼長和起始點，且效果明顯，容錯性較好。

1 循環碼的定義及分析

定義1[12]：設X=(x1,…,xd)和Y=(y1,…,yd)是d維空間中的兩個點，相似性度量函數為Hsim(X,Y)，該函數表示對象之間的相似程度，函數值越小，對象之間的差異越大，即相似性越小；相反，相似性越大。其表達式如下

(1)

定義2[13]：一個n重子空間Vn,k∈Vn，若對任何一個V=(an-1,an-2,…,a0)∈Vn,k，恒有V1=(an-2,an-3,…,a0,an-1)∈Vn,k，則稱Vn,k為循環子空間或循環碼。GF(q)(q為素數或素數的冪)上的[n,k]循環碼中，存在唯一的n-k次多項式g(x)=xn-k+gn-k-1xn-k-1+…+g1x+g0，且每一碼多項式C(x)都是g(x)的倍式，這相當于

C(x)=m(x)xn-k+r(x)=0(modg(x))

(2)

式中：m(x)=mk-1xk-1+mk-2xk-2+…+m1x+m0是信息多項式；r(x)=rn-k-1xn-k-1+…+r1x+r0是校驗多項式。

定義3[13]：按照信息碼元在編碼后是否保持原來的形式不變，可劃分為系統碼和非系統碼。系統碼的G矩陣為G=[IK,P]，左邊是k×k階單位方陣。根據生成矩陣G可以寫出其校驗矩陣H=[In-p,P′]，其中P′是P的轉置。

定義4[13]：一個碼字的重量等于該碼字中非零元素的個數。在二進制碼中碼重就是二元序列中含有“1”的個數。設Ai是[n,k,d]分組碼中重量為i的碼字數目，則集合{A0,A1,…,An}稱為該分組碼的重量分布。碼重分布概率Pi是重量為i的碼字個數在碼字總數中出現的概率。

2 循環碼的參數估計

對于循環碼而言，碼組內各碼元之間存在較強的線性約束關系，且不同碼重的碼組分布是非等概率的，而對于隨機序列來說，并不是任意組合的碼字都會出現，根據碼重分布和隨機序列碼重分布概率存在較大的差距進行碼長和起始點的識別。

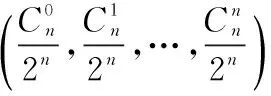
(3)

經上述分析：在起始點已知時，當碼重相似性度量函數值越大，說明實際序列與隨機序列越相似，差異性就越小，則該碼長不是真實碼長或碼長的整數倍。相反，該值越小，則該碼長為真實碼長或碼長的整數倍，即可識別碼長。同理，碼長已知時，起始點處對應的碼重相似性度量函數值越小，即可識別起始點。

2.1 起始點為先驗知識下識別碼長

在實際工程中，通過幀同步信息可以找到碼字的起始位置q，因此，本節已知起始點來識別碼長。

已知起始點時，假設接收序列長度為N，則碼長識別步驟如下：

1)初始化估計的碼長為n，變化范圍為1～t，t的值根據實際情況選定，將接收序列按估計碼長放入矩陣中，列數為n，行數為m，且行數m=[(N-q+1)/n]，即碼字數，其中m>4n， 記為

Ca={c1+(m-a)n,c2+(m-a)n,…,cn+(m-a)n}

(4)

式中：a=m,m-1,…,1。

2)將每個碼字Ca中的元素進行累加計算碼重，即

Ha=c1+(m-a)n+c2+(m-a)n+…+cn+(m-a)n

(5)

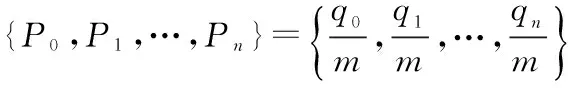
3)根據式(3)計算Hsim(P,C)的值。

4)n=n+1，轉到步驟(1)，計算不同碼長估計值n對應的碼重相似性度量函數Hsim(P,C)的值。

5)計算完成后，找出Hsim(P,C)最小值對應的碼長估計值n即為真實碼長。

2.2 碼長為先驗知識下識別起始點

碼長n可以對接收的數據流處理得到，因此，識別起始點則為關鍵。

碼長已知，則起始點識別步驟如下：

1)初始化估計的起始點為第q位，q的取值范圍為1～n+1， 將接收序列N按確定的碼長n放入矩陣中，列數為n，行數為m，且行數m=[(N-q+1)/n]，即碼字數，記為

Ca={c1+(m-a)n,c2+(m-a)n,…,cn+(m-a)n}

(6)

式中：a=m,m-1,…,1。

2)同上述碼長的識別步驟2)和3)相同。

3)q=q+1，轉到步驟1)繼續執行，直到q=n+1，比較上述計算的結果，找出Hsim(P,C)最小值對應的q即為碼字起始點。

2.3 計算生成矩陣

由碼重相似性度量函數識別出碼長和起始點，為達到無誤碼字最大化，選取在編碼識別過程中出現碼重概率最大的碼字排列成矩陣形式，并對矩陣進行初等行變換，應采取模二運算，化簡后的形式為[IkP]，m-k余下行全部化為0。

求得生成矩陣G后，即可得到生成多項式，為驗證其正確性，可通過式(2)來說明。當接收碼字無誤碼時，由接收碼字得到其碼字多項式，并除以生成多項式，其中除法運算中減法也是模二和運算，若余式為0，則式(2)關系成立；相反，式(2)不成立。在實際噪聲環境下，根據傳輸信道誤碼率設定判決門限T，當T小于式(2)成立的概率時，所得生成矩陣正確。

3 仿真驗證

3.1 起始點已知，識別碼長

為了驗證識別方法的正確性，選取誤碼率Pe=0.01和Pe=0.10的(7，4)、Pe=0.01的(15，5)、Pe=0.05的(31，16)4種循環碼，碼元個數為104，運用MATLAB進行試驗仿真，結果如圖1所示。

經圖1可以看出，在一定的數據量條件下，由于碼組內具有完整的線性約束關系，當遍歷碼長為真實值或其倍數時，分組后不同碼重的碼字序列與隨機序列碼重分布概率相差較大，所以，相似性度量函數值較小，當首次出現最小值時，則為真實碼長n。相反，當不是真實值或其倍數時，分組后不同碼重的碼字序列接近隨機序列碼重分布概率，所以，相似性度量函數值變化相對平穩。同時，在低誤碼率時，即0.001～0.010時，能正確識別碼長且效果較明顯，而且再次出現低值的點，可以識別2～3整數倍的碼長。但隨誤碼率的增加，雖可以明顯的識別真實碼長，但碼長整數倍的點，識別效果不明顯，可見，對于真實碼長，該識別方法能適應較高的誤碼率，且識別效果明顯。

3.2 碼長已知，識別起始點

為驗證識別方法的正確性，選取誤碼率Pe=0.05和Pe=0.1的(7，4)、Pe=0.08的(15，5)、Pe=0.03的(31，16)、Pe=0.01的(127，50)4種循環碼，碼元個數為104，運用MATLAB進行試驗仿真，結果如圖2所示。

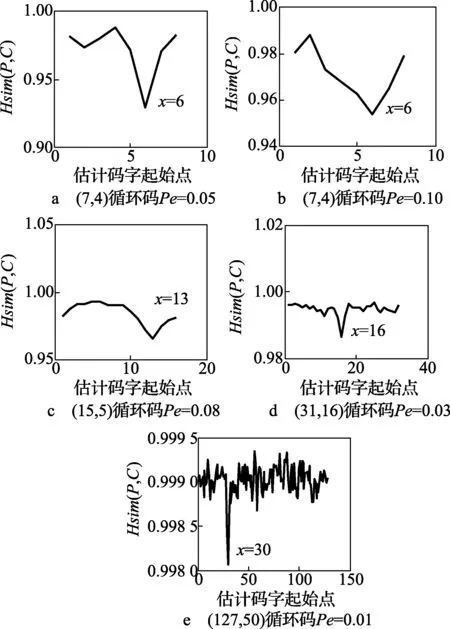
圖2 碼字起始點識別仿真圖

經圖2可以看出，碼長已知，編碼碼字不同，所選誤碼率不同，依次對假設的起始點遍歷，根據碼重相似性函數值的大小可判斷出起始點的位置。對于上述4種循環碼，雖誤碼率不同，但都較明顯的識別出起始點，可以看出，碼重相似度最小值分別出現在6、13、16、30，則相似度較小，碼組內線性約束關系較強，則該點即為起始點。對于(31，16)和(127，50)循環碼，誤碼率較前者較低，由于選取碼元個數相同，所以二者實驗仿真所用的碼字數相對于前者較少，即誤碼率選取要小一些，才能保證正確識別碼字起始點，若要求在高誤碼條件下，可以選取較多的碼字進行仿真即可，可見，該方法可在高誤碼率的條件下正確識別碼字起始點，識別效果明顯且容錯性較好。

3.3 結果分析

在誤碼率Pe=0.01的條件下，選取碼長與碼率不同的碼字進行100次蒙特卡洛仿真實驗，得到不同碼的正確識別概率如表1所示。

由表1可知：根據碼重相似性度量函數值可以正確識別碼長和起始點，但碼長與碼率的不同會直接影響到識別的性能。碼長與碼字個數相同時，低碼率的碼字識別效果較明顯，容錯性能較好，例如碼長為15的碼字；碼長與碼率相同時，選取較多的碼字，碼長和起始點的識別效果會有較明顯的提升，例如碼長為127的碼字；碼字個數相同，碼率相近時，例如(63，24)與(127，50)兩種碼字，前者碼長識別率高于后者。總體可得，該算法更適合于低碼率的中短碼進行識別。

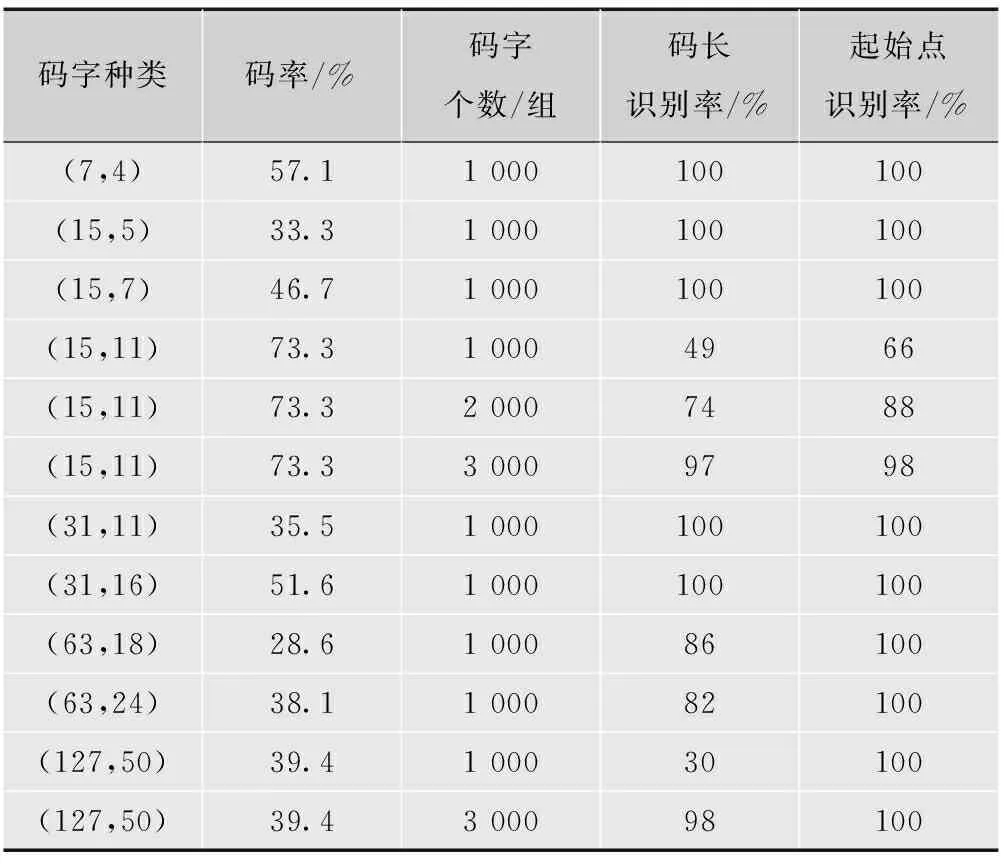
表1 誤碼率Pe=0.01時識別概率

4 生成矩陣求解及驗證

針對有誤碼的情況，選取200個碼字，在含有Pe=0.015的誤碼條件下，以(15，5)循環碼為例，利用識別碼長2.1節描述中的第2)步記錄碼重i出現的次數記為qi，則在碼字中占的概率值如圖3所示。

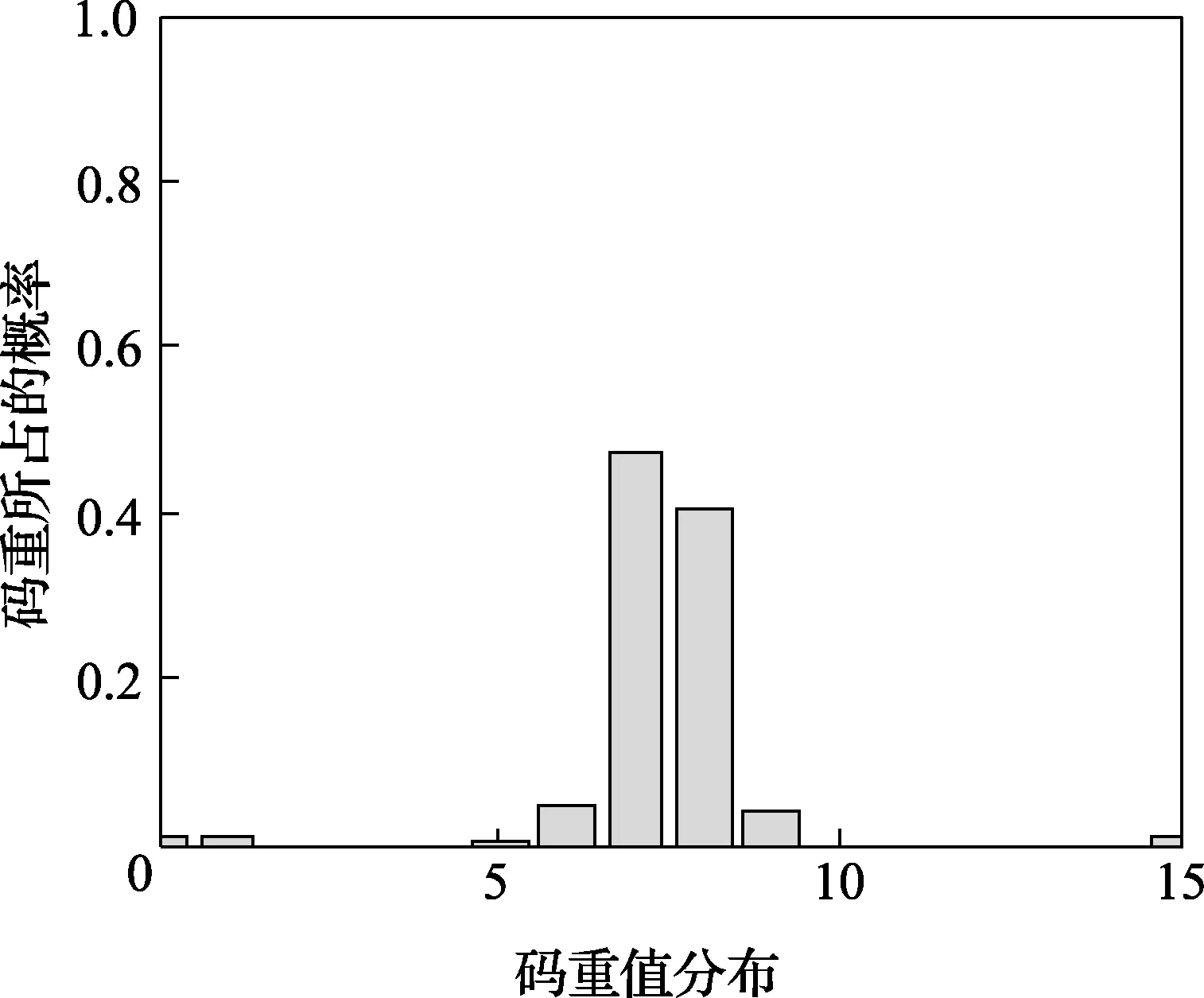
圖3 (15，5)循環碼碼重值分布仿真圖

經圖3可以看出，當碼字的碼重為7和8時所占概率較大，因此，選取這兩種碼重對應的碼字構成m行n列(m>n)的矩陣，采用模二運算對矩陣進行化簡，獲得生成矩陣G

(7)

由循環碼的定義可知，生成矩陣G的最后一行即為生成多項式的系數，即生成多項式為g(x)=x10+x8+x5+x4+x2+x+1。為檢驗G的正確性，可利用生成多項式g(x)來驗證。首先，設置判決門限T，常規信道誤碼率設定為2×10-2，計算200個碼字中共包含60個錯誤碼元，設定不同碼字中含有一個錯誤碼元，計算出錯誤碼字占所有碼字的比例為30%，可得判決門限T=1-30%=70%，即當式(2)成立的概率大于T時，可認為G求解正確。在上述試驗中，當n=15時，所有碼字利用式(2)計算出余式為0的概率為87%，即大于70%，可見，生成矩陣G的求解正確，即可完成識別。

5 容錯性比較分析

在誤碼條件下，對于不同參數的系統循環碼，在誤碼率取值不同的條件下，選取2×104個碼字進行1 000次蒙特卡洛仿真實驗，得出碼長和起始點識別率，如圖4、圖5所示：根據碼重相似性度量函數識別碼長和起始點，明顯看出，(7，4)和(15，5)在誤碼率為0.20時，碼長和起始點識別率高達95%；(31，16)在誤碼率為0.05時，識別率高達90%；(63，18)在誤碼率為0.01時，識別率高達90%。可以得出，隨著循環碼的碼長與碼率的增加，碼字之間的線性約束關系降低，導致識別概率逐漸減小；同時，該算法能在高誤碼率條件下，能有效地識別碼長和起始點。

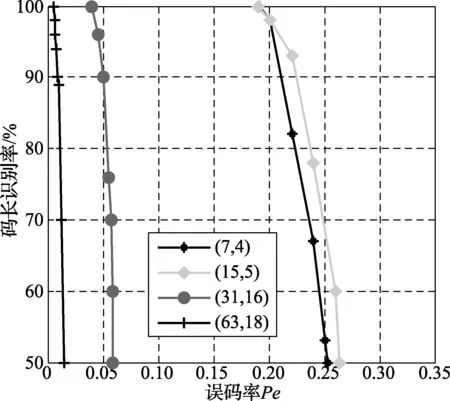
圖4 碼長識別概率曲線圖

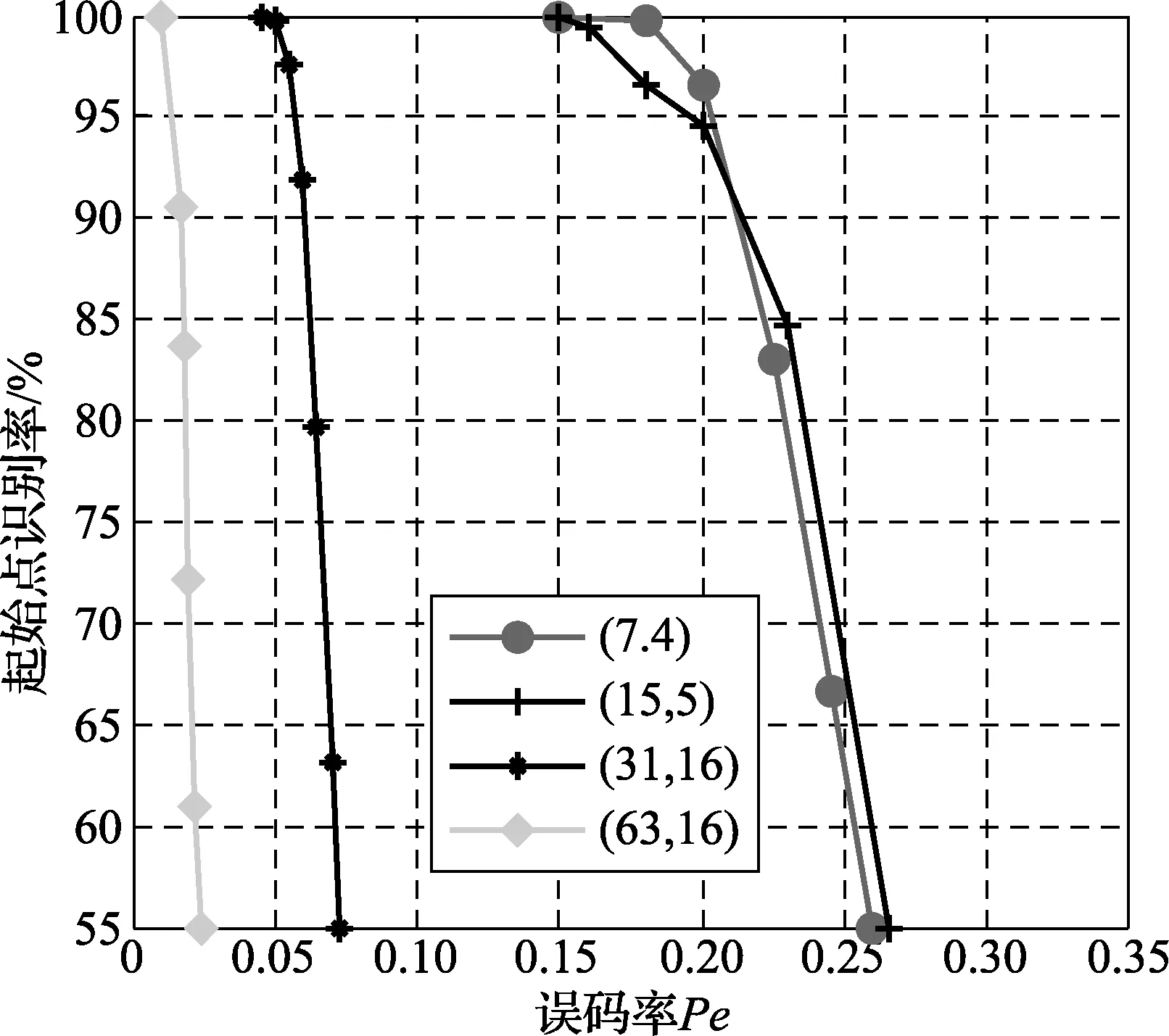
圖5 起始點識別概率曲線圖

循環碼也是一種線性分組碼，分別選取2×104個4種長度的循環碼為實驗對象，進行仿真，圖6和圖7為文獻[6]識別碼長和起始點的概率曲線圖，比較圖5和圖6，在碼字個數與種類相同時，選取相同的起始點識別概率，可以看出，本文的誤碼率在高于文獻[6]時，起始點仍能夠正確識別。以(7，4)典型循環碼為例，當起始點識別概率達到100%時，本文算法的誤碼率為0.15，而文獻[6]的誤碼率為0.08，可見本文算法在識別起始點所體現出的容錯性更有優勢。在起始點已知時，圖8為文獻[11]利用碼重分布概率方差識別碼長概率曲線圖，選取數目種類相同的碼字，對文獻[6，11]和本文提出的碼長識別算法進行比較，圖9為不同算法的90%識別誤碼率上限[14]曲線圖，以碼長15為例，本文的誤碼率為23%，文獻[11]的誤碼率為8%，文獻[6]的誤碼率為3%，仿真結果表明，在碼長取值相同的條件下，本文識別算法抗誤碼的能力高于之前的算法，容錯性較好。

圖6 文獻[6]起始點識別概率圖

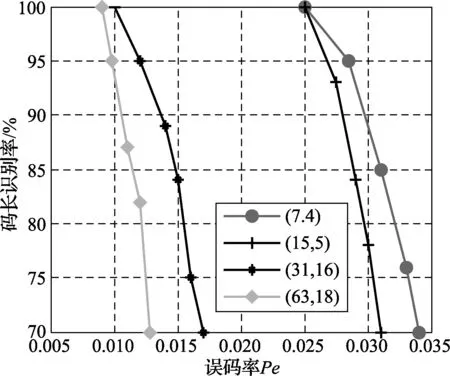
圖7 文獻[6]碼長識別概率曲線圖

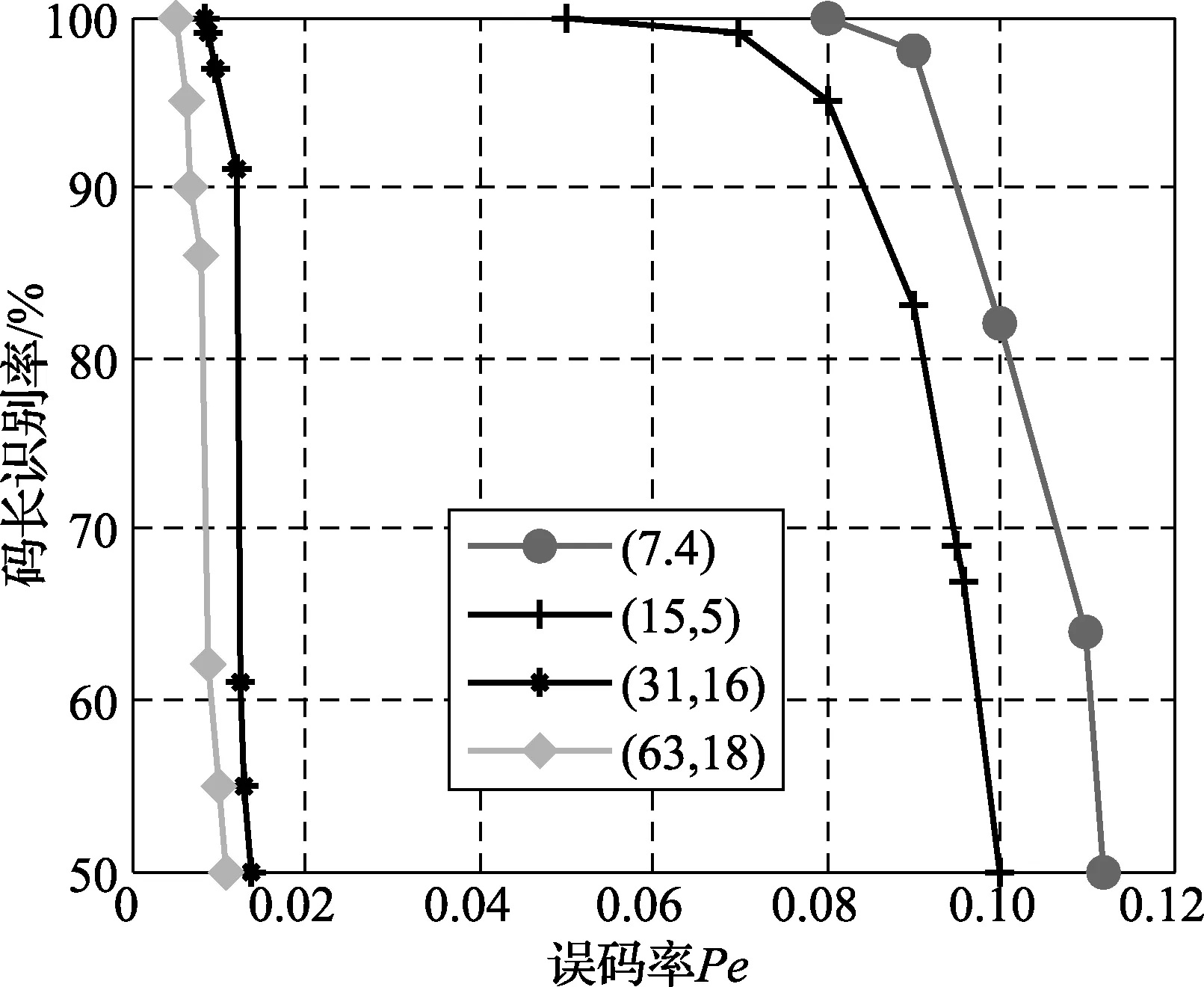
圖8 文獻[11]碼長識別概率曲線圖

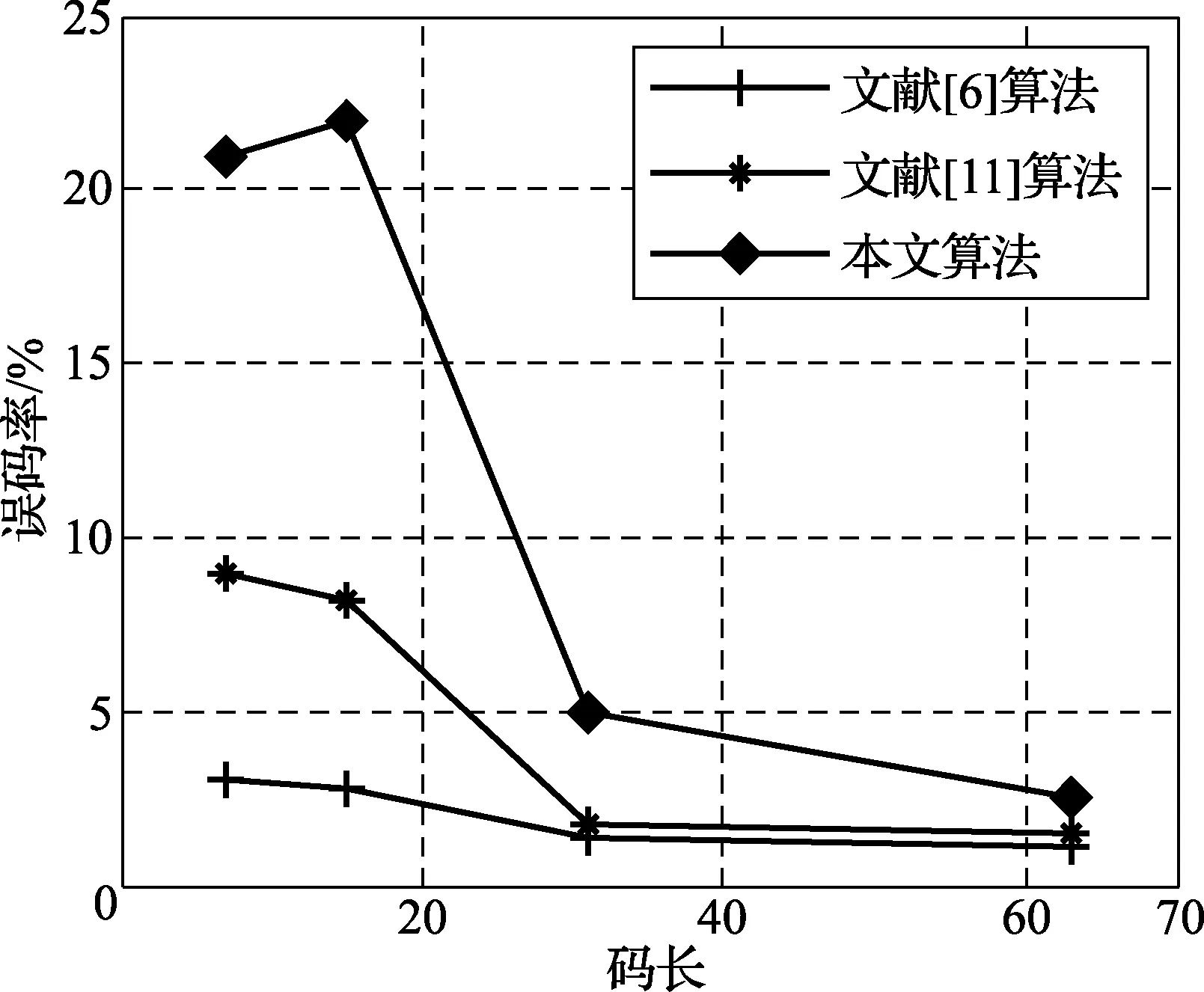
圖9 不同算法的90%識別誤碼率上限

6 結論

本文依據碼重分布的特點，根據數據挖掘中相似度的方法，實現對碼長和起始點的識別，在此基礎上，利用優化傳統的矩陣化簡識別生成矩陣，即得出生成多項式，并設定判決門限完成生成多項式的正確檢驗，進而實現對系統循環碼參數的識別。最后，在不同的先驗知識和不同的誤碼率下，對系統循環碼進行大量的仿真實驗，并與其他算法進行比較，結果表明，該算法無復雜的計算，對低碼率的中短碼在誤碼率為0.01時識別效果較明顯，具有較好的容錯性，在增加碼組數量的同時，碼長和起始點的識別率得到較大的提高。

[1] 張永光，樓才義.信道編碼及其識別分析[M].北京：電子工業出版社，2010.

[2] 王蘭勛，佟婧麗，孟祥雅.一種線性分組碼參數的盲識別方法[J].電視技術，2014，38(9)：188-192.

[3] 宋鏡業.信道編碼識別技術研究[D].西安：西安電子科技大學，2009.

[4] 昝俊軍，李艷斌.低碼率二進制線性分組碼的盲識別[J].無線電工程，2009，39(1)：19-24.

[5] 陳金杰，楊俊安.一種對線性分組碼編碼參數的盲識別方法[J].電路與系統學報，2013，18(2)：248-254.

[6] 陳金杰，計時鐘，楊俊安.高誤碼條件下線性分組碼的盲識別[J].應用科學學報，2013，31(5)：459-467.

[7] 王蘭勛，李丹芳，汪洋.二進制本原BCH碼的參數盲識別[J].河北大學學報，2012，32(4)：416-420.

[8] 楊曉靜，聞年成.基于碼根信息差熵和碼根統計的BCH碼識別方法[J].探測與控制學報，2010，32(3)：69-73.[9] 聞年成，楊曉靜.采用秩統計和碼根特征的二進制循環碼盲識別方法[J].電子信息對抗技術，2010，25(6)：26-29.

[10] 王磊，胡以華，王勇，等.基于碼重分布的系統循環碼識別方法[J].計算機工程與應用，2012，48(7)：150-153.

[11] 鄧瑞瑞，汪立新.基于碼重分布概率方差的循環碼識別方法[J].太赫茲科學與電子信息學報，2013，11(5)：792-796.

[12] 楊風召.高維數據挖掘技術研究[M].南京：東南大學出版社，2007.

[13] 王新梅，肖國鎮.糾錯碼—原理與方法(修訂版)[M].西安：西安電子科技大學出版社，2001.

[14] 王平，曾偉濤，陳健，等.一種利用本原元的快速RS碼盲識別算法[J].西安電子科技大學學報，2013，40(1)：105-110.

王蘭勛(1956— )，教授，主要從事數字通信與信息編碼方面研究；

熊政達(1989— )，女，碩士生，主研信道編碼盲識別；

佟婧麗(1989— )，女，碩士生，主研信道編碼盲識別。

責任編輯：時 雯

Blind Recognition of System Cyclic Codes Parameters Based on Similarity

WANG Lanxun，XIONG Zhengda，TONG Jingli

(CollegeofElectronicandInformationalEngineering，HebeiUniversity，HebeiBaoding071002，China)

In view of the problem of the blind recognition of system cyclic code parameters， an algorithm based on a similarity measuring function by using the method of data mining is proposed. Firstly，the code length and starting point are identified by the characteristics based on the similarity of code weight that is used by the most notable differences whose similarity of code weight distribution between the actual sequence and random sequence under the different prior knowledge.On this basis， the generator matrix is solved through the method of optimizing the traditional simplification of matrices and then employing the relationship between the code word polynomial and generating polynomial to set a decision thresholdT，the blind recognition of system cyclic code is finally realized.Simulation results show that the method has better recognition effect with BER of 0.01.

system cyclic code； blind recognition； similarity of code weight distribution； generator matrix

【本文獻信息】王蘭勛，熊政達，佟婧麗.基于相似度對系統循環碼參數的盲識別[J].電視技術,2015，39(11).

河北省自然科學基金項目(F2014201168)

TN911.22

A

10.16280/j.videoe.2015.11.008

2014-10-25