巖石的外觀體積和流固兩相壓縮系數

李傳亮，朱蘇陽

（西南石油大學石油與天然氣工程學院，成都610599）

討論與爭鳴

巖石的外觀體積和流固兩相壓縮系數

李傳亮，朱蘇陽

（西南石油大學石油與天然氣工程學院，成都610599）

巖石有3個體積和3個應力，因此巖石有多個壓縮系數。油藏工程主要研究了孔隙壓縮系數的計算和應用問題，對其他的壓縮系數研究甚少。對外觀體積和流固兩相的壓縮系數進行了研究，并分別推導出了它們的計算公式。巖石外觀體積對孔隙壓力的壓縮系數與孔隙壓縮系數相同。巖石外觀體積對外壓的壓縮系數是孔隙度和骨架壓縮系數的函數。巖石流固兩相壓縮系數為流體壓縮系數和骨架壓縮系數的加權調和平均值或加權倒數算術平均值，孔隙度為權值。

巖石；孔隙體積；孔隙度；壓縮系數；外觀體積；孔隙壓力

0　引言

巖石不同于普通固體，巖石內部有孔隙，而普通固體則沒有孔隙［1］。孔隙是巖石儲存流體的地方，巖石受壓后將被壓縮，壓縮系數是巖石彈性能量大小的標志［2］。

巖石有多個壓縮系數，油藏工程只使用孔隙壓縮系數［3-6］，其他壓縮系數都不使用。因此，關于巖石壓縮系數的研究，也一直都是針對孔隙壓縮系數而展開的［7-10］。

其他領域也使用巖石的壓縮系數，主要是使用巖石外觀體積的壓縮系數。外觀體積的壓縮系數一般通過實驗進行測量，目前還沒有理論計算公式。

若巖石與飽和于其中的流體一起被壓縮，則需要確定流固兩相壓縮系數及其與流體壓縮系數和固體壓縮系數的關系，但目前還沒有關于這方面的報道。

筆者的目的就是要解決巖石外觀體積壓縮系數和巖石流固兩相壓縮系數的計算問題。

1壓縮系數定義

巖石有3個體積：骨架體積、孔隙體積和外觀體積（圖1）。這3個體積滿足下面的關系式：

式中：Vs為骨架體積，m3；Vp為孔隙體積，m3；Vb為外觀體積，m3。

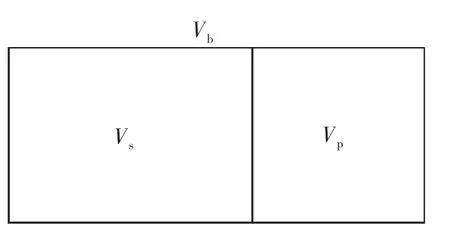
圖1巖石體積構成圖Fig.1 Volumes in rocks

巖石有3個應力：骨架應力、內應力（孔隙壓力、內壓）和外應力（外壓）（圖2）。這3個應力滿足下面的關系式［11-12］：

式中：σ為外應力，MPa；p為孔隙壓力，MPa；σs為骨架應力，MPa；φ為巖石孔隙度，無因次。

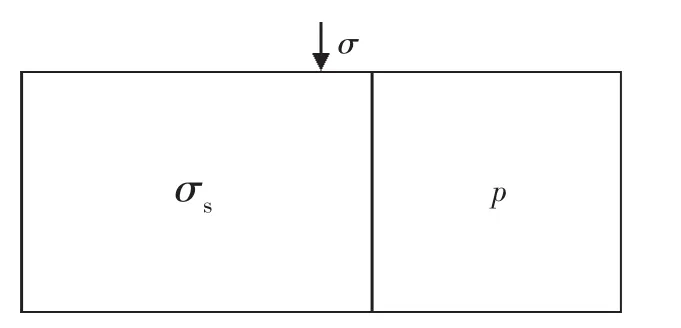
圖2巖石應力構成圖Fig.2 Stresses in rocks

當巖石任一應力發生變化時，巖石的3個體積都將發生變化，因此，巖石有9個壓縮系數［1］，即式中：i代表體積，i取b，s，p時分別表示外觀體積、骨架體積和孔隙體積；j代表應力，j取b，s，p時分別表示外應力、骨架應力和內應力。當j取b，s時，n= 1；當j取p時，n=2。如cpb表示孔隙體積對外應力的壓縮系數，cpp表示孔隙體積對孔隙壓力的壓縮系數。當這2下標相同時就簡化成1個下標，如cpp寫成cp。

由于式（1）和式（2）的約束關系，3個體積和3個應力中都只有2個是獨立的，因此，9個壓縮系數中只有4個是獨立的。

2骨架和孔隙壓縮系數

骨架顆粒是巖石中的固體成分。與流體相同，固體骨架的壓縮系數可以定義為

式中：cs為固體骨架的壓縮系數，MPa-1。

根據固體力學理論，在彈性變形條件下固體骨架的壓縮系數可用下式計算，即

式中：ν為固體骨架的泊松比，無因次；Es為固體骨架的彈性模量，MPa。

彈性模量的大小反映了固體骨架的硬度，彈性模量越大，骨架就越硬，其壓縮系數也就越小。固體骨架的壓縮系數不需要按式（4）進行計算或實際測量，只需要在測量巖石的力學參數之后按式（5）進行計算即可。一般情況下，實驗室不會測量骨架的力學參數，而是測量整個巖石的力學參數，然后通過下式進行轉換［13］：

式中：E為巖石的彈性模量，MPa。

油藏工程關心的是，在外應力為常數的情況下巖石孔隙體積隨孔隙壓力的變化情況，即孔隙體積的壓縮系數：

由式（7）定義的孔隙壓縮系數也不需要進行實際測量，而只需按下式進行計算即可［13-15］：

由式（8）可看出，孔隙壓縮系數是孔隙度和骨架壓縮系數的反映。對于骨架彈性模量為10 000MPa的巖石，其孔隙壓縮系數隨孔隙度的變化曲線如圖3所示。

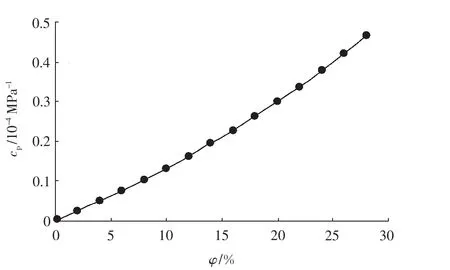
圖3孔隙壓縮系數曲線Fig.3 Pore com pressibility versus porosity

3外觀體積壓縮系數

巖石外觀體積的壓縮系數可以分別定義為：①在恒定外壓的情況下，單位孔隙壓力的外觀體積變化率；②在恒定內壓的情況下，單位外壓的外觀體積變化率。因此，外觀體積有2個壓縮系數。

外觀體積對內壓的壓縮系數為

式中：cbp為外觀體積對孔隙壓力的壓縮系數，MPa-1。

外觀體積對外壓的壓縮系數為

式中：cb為外觀體積對外應力的壓縮系數，MPa-1。

3.1恒定外壓

在恒定外壓情況下，巖石因內壓降低而被壓縮，當內壓由p1降到p2，骨架應力將由σs1升到σs2（圖4）。巖石的壓縮皆因骨架的壓縮所致。若骨架沒有變化，則巖石的外觀體積也不會變化。在本體變形的情況下，巖石的外觀體積隨骨架體積一起壓縮，巖石的孔隙度并不會發生變化［16-17］。因此，式（9）可以寫為

圖4外觀體積隨內壓壓縮圖Fig.4 Compression ofbulk volumew ith pore pressure

根據式（2）可得

將式（12）代入式（11）可得

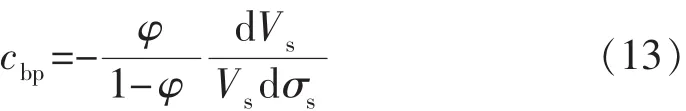
再結合式（4），可得出外觀體積對孔隙壓力的壓縮系數計算公式，即

由式（14）和式（8）可以看出，巖石外觀體積對孔隙壓力的壓縮系數與孔隙壓縮系數完全相同。

3.2恒定內壓

在恒定內壓情況下，巖石因外壓升高而被壓縮，同時排出其中的流體，當外壓由σ1升到σ2，骨架應力將由σs1升到σs2（圖5）。在本體變形的情況下，巖石外觀體積隨骨架體積一起壓縮。因此，式（10）可以寫為

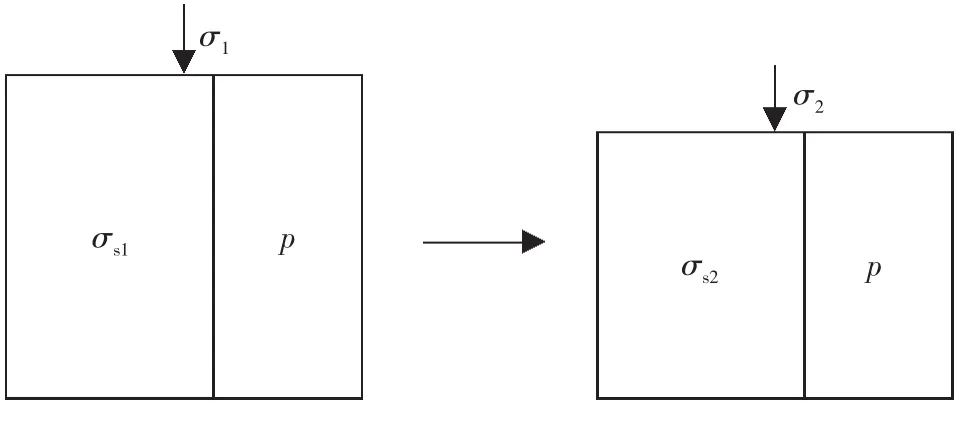
圖5外觀體積隨外壓壓縮圖Fig.5 Compression ofbulk volumew ith outer pressure

根據式（2）可得

將式（16）代入式（15）可得

再結合式（4），可得出外觀體積對外應力的壓縮系數計算公式，即

由式（18）可以看出，巖石外觀體積的壓縮系數是孔隙度和骨架壓縮系數的反映，孔隙度越大，外觀體積的壓縮系數就越大，即巖石越容易被壓縮。當φ趨于0時，則巖石接近于普通固體，cb趨于cs。外觀體積對外壓的壓縮系數曲線如圖6所示。

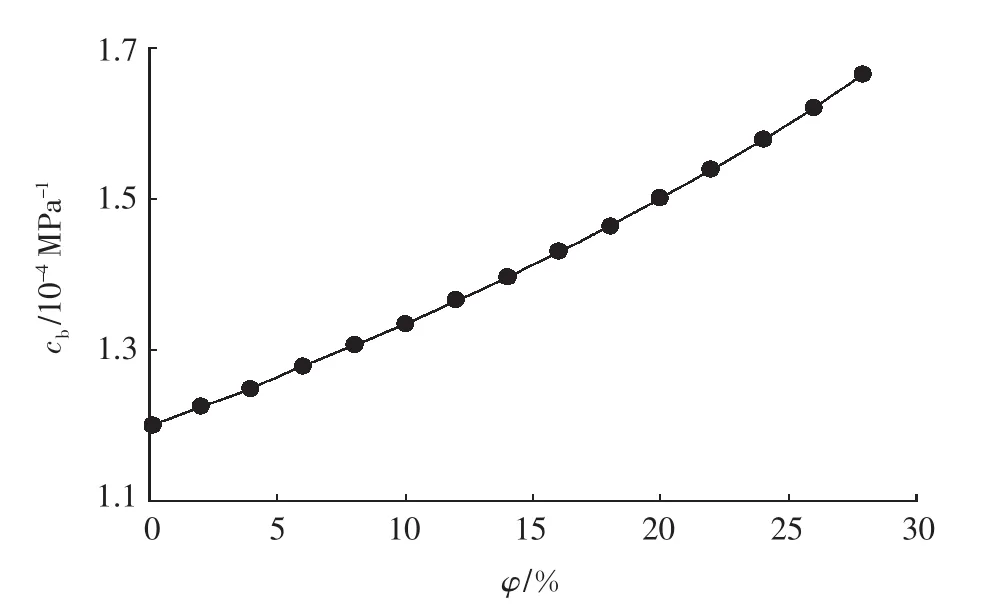
圖6外觀體積對外壓的壓縮系數曲線Fig.6 Compressibility curve ofbulk volume to outer pressure versus porosity

4　流固兩相壓縮系數

不論是孔隙壓縮系數、骨架壓縮系數，還是外觀體積壓縮系數，都是單相壓縮系數。當孔隙流體和巖石骨架作為一個整體進行壓縮時，在流體無法排出的情況下，就是流固兩相的壓縮問題。流固兩相壓縮系數除了與孔隙度有關外，還與流體和骨架的壓縮系數有關。當外壓由σ1升到σ2，骨架應力將從σs1升到σs2，孔隙壓力將從p1升到p2（圖7）。流固兩相的壓縮系數定義為

式中：cbt為流固兩相壓縮系數，MPa-1；Vbt為流固兩相的外觀體積，m3。

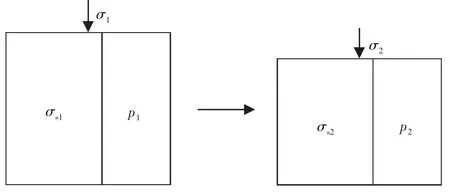
圖7　巖石流固兩相壓縮圖Fig.7 Two phase com pression of fluid-solid of rocks

流固兩相的外觀體積其實就是巖石的外觀體積，即Vbt=Vb。在本體變形的情況下，巖石外觀體積隨骨架體積一起壓縮。因此，式（19）可以寫為

將式（20）改寫為

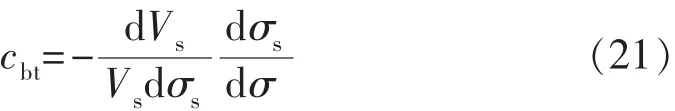
再結合式（4），式（21）可以寫為

由于巖石壓縮過程中流體無法排出，因此，孔隙體積的減少量等于流體體積的壓縮量，則有

式中：cf為流體壓縮系數，MPa-1。

對式（2）兩側求導數，即

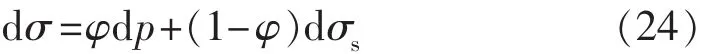
將式（23）代入式（24）可得

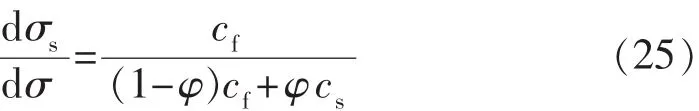
將式（25）代入式（22），可得流固兩相壓縮系數，即

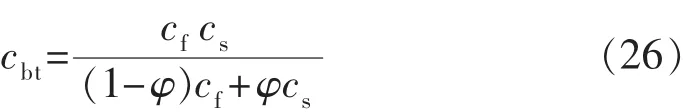
式（26）也可以寫為

式（27）就是巖石流固兩相壓縮系數與流體和骨架壓縮系數的關系方程。由式（27）可以看出，流固兩相的壓縮系數為流體壓縮系數和骨架壓縮系數的加權調和平均值或加權倒數算術平均值，孔隙度為權值。當φ趨于0時，巖石接近于普通固體，cbt趨于cs；當φ趨于1時，巖石接近于流體，cbt趨于cf。式（27）將流體、固體和多孔介質巖石統一起來。流體可以是水，也可以是油或氣。彈性模量為10 000MPa的固體骨架壓縮系數為1.2×10-4MPa-1，若流體為油，壓縮系數取10×10-4MPa-1；若流體為氣，壓縮系數取100×10-4MPa-1；此時流固兩相的壓縮系數隨孔隙度的變化曲線如圖8所示。從圖8可以看出，流體性質對流固兩相壓縮系數產生了很大的影響。

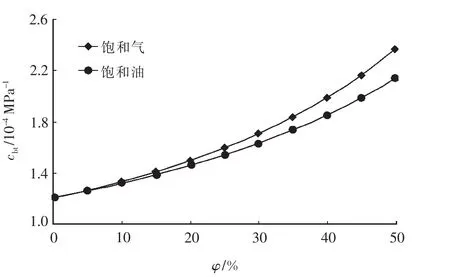
圖8　巖石流固兩相壓縮系數曲線Fig.8 Two phase compressibility of fluid-solid of rocksversus porosity

5　結論

（1）巖石外觀體積的壓縮系數是孔隙度和骨架壓縮系數的函數。

（2）巖石外觀體積對內壓的壓縮系數與孔隙壓縮系數相同，對外壓的壓縮系數為式（18）。

（3）巖石流固兩相的壓縮系數為流體壓縮系數和骨架壓縮系數的加權調和平均值或加權倒數算術平均值，孔隙度為權值，即式（27）。

（References）：

［1］李傳亮.油藏工程原理［M］.第2版.北京：石油工業出版社，2011：71-90.LiChuanliang.Fundamentalsofreservoirengineering［M］.2nd Edition. Beijing：Petroleum Industry Press，2011：71-90．

［2］李傳亮，朱蘇陽.油藏天然能量評價新方法［J］.巖性油氣藏，2014，26（5）：1-4. LiChuanliang，Zhu Suyang.A new evaluationmethod of reservoir energy［J］.Lithologic Reservoirs，2014，26（5）：1-4.

［3］李傳亮，姚淑影，李冬梅.油藏工程該使用哪個巖石壓縮系數？［J］.西南石油大學學報：自然科學版，2010，32（2）：182-184. LiChuanliang，Yao Shuying，LiDongmei.Which rock compressibility should beused in reservoirengineering？［J］.Journal of Southwest Petroleum University：Science&Technology Edition，2010，32（2）：182-184.

［4］李傳亮.巖石應力敏感指數與壓縮系數之間的關系式［J］.巖性油氣藏，2007，19（4）：95-98. Li Chuanliang.A theoretical formula of stress sensitivity index with compressibility of rock［J］.Lithologic Reservoirs，2007，19（4）：95-98.

［5］李傳亮.地層抬升會導致異常高壓嗎？［J］.巖性油氣藏，2008，20（2）：124-126. LiChuanliang.Canupliftresultinabnormalhigh pressure in formation？［J］.Lithologic Reservoirs，2008，20（2）：124-126.

［6］李傳亮，涂興萬.儲層巖石的2種應力敏感機制［J］.巖性油氣藏，2008，20（1）：111-113. LiChuanliang，Tu Xingwan.Two typesofstresssensitivitymechanisms for reservoir rocks［J］.Lithologic Reservoirs，2008，20（1）：111-113.

［7］孫良田.油層物理實驗［M］.北京：石油工業出版社，1992：79-88. Sun Liangtian.Petrophysics experiments［M］.Beijing：Petroleum Industry Press，1992：79-88．

［8］秦同洛，李璗，陳元千.實用油藏工程方法［M］.北京：石油工業出版社，1989：64-65. Qin Tongluo，LiDang，Chen Yuanqian.Practical reservoirengineering［M］.Beijing：Petroleum Industry Press，1989：64-65．

［9］李傳亮.實測巖石壓縮系數偏高的原因分析［J］.大慶石油地質與開發，2005，24（5）：53-54. LiChuanliang.Results interpretation ofhighermeasured rock compressibility［J］.Petroleum Geology&Oilfield Development in Daqing，2005，24（5）：53-54.

［10］HallHN.Compressibility of reservoir rocks［J］.Trans.，AIME，1953，198：309-311.

［11］李傳亮.多孔介質的應力關系方程——答周大晨先生［J］.新疆石油地質，2002，23（2）：163-164. LiChuanliang.Equations for stress relations in porousmedium—In reply toMr Zhou Dachen［J］.Xinjiang Petroleum Geology，2002，23（2）：163-164.

［12］李傳亮，孔祥言，徐獻芝，等.多孔介質的雙重有效應力［J］.自然雜志，1999，21（5）：288-292. Li Chuanliang，Kong Xiangyan，Xu Xianzhi，et al.Dual effective stresses of porousmedia［J］.Chinese Journal of Nature，1999，21（5）：288-292．

［13］李傳亮.巖石壓縮系數測量新方法［J］.大慶石油地質與開發，2008，27（3）：53-54. LiChuanliang.A newmeasurementmethod of rock compressibility［J］.Petroleum Geology&Oilfield Development in Daqing，2008，27（3）：53-54.

［14］李傳亮.巖石壓縮系數與孔隙度的關系［J］.中國海上油氣（地質），2003，17（5）：355-358. LiChuanliang.The relationship between rock compressibility and porosity［J］.ChinaOffshoreOiland Gas（Geology），2003，17（5）：355-358.

［15］李傳亮.巖石的壓縮系數問題［J］.新疆石油地質，2013，34（3）：354-356. Li Chuanliang.Compressibility of reservoir rocks［J］.Xinjiang Petroleum Geology，2013，34（3）：354-356.

［16］李傳亮.巖石欠壓實概念質疑［J］.新疆石油地質，2005，26（4）：450-452. LiChuanliang.Discussion ofundercompaction of rocks［J］.Xinjiang Petroleum Geology，2005，26（4）：450-452.

［17］李傳亮.巖石本體變形過程中的孔隙度不變性原則［J］.新疆石油地質，2005，26（6）：732-734. LiChuanliang.The principleof rock porosity invariability in primary deformation［J］.Xinjiang Petroleum Geology，2005，26（6）：732-734.

（本文編輯：王會玲）

Com pressibility coefficientsof bulk volumeand fluid-solid of rocks

LI Chuanliang，ZHU Suyang
（SchoolofPetroleum Engineering，SouthwestPetroleum University，Chengdu 610599，China）

Rockshave three volumesand three stresses，so have several compressibility coefficients.Pore compressibility and itsapplicationshavebeenmainly studied in reservoirengineering，and othersareseldom touched.Thispaper focused on the compressibilitiesofbulk volume and fluid-solid of rocks，and derived their calculation formula.The compressibility ofbulk volume of rocks to pore pressure is the same ofpore compressibility of rocks.The compressibility ofbulk volume of rocks to outer pressure is the function ofporosity and skeleton compressibility of rocks.The two-phase compressibility of fluid-solid of rocks isporosity-weighted harmonicmean of fluid compressibility and skeleton compressibility，or porosityweighted arithmeticmean of reciprocalsof fluid compressibility and skeleton compressibility.

rock；porevolume；porosity；compressibility；bulk volume；porepressure

TE312

A

1673-8926（2015）02-0001-05

2014-12-05；

2015-02-02

國家科技重大專項“多層疏松砂巖氣藏開發關鍵技術”（編號：2011ZX05027-003-01）資助

李傳亮（1962-），男，博士，教授，主要從事油藏工程方面的教學與科研工作。地址：（610599）四川省成都市西南石油大學石油與天然氣工程學院。電話：（028）83033291。E-m ail：cllipe@qq.com。