分數階Fourier變換在信號處理中的應用研究

王春陽，劉雪蓮

（長春理工大學，電子信息工程學院，長春　130022）

分數階Fourier變換在信號處理中的應用研究

王春陽，劉雪蓮

（長春理工大學，電子信息工程學院，長春130022）

本文綜述了分數階Fourier變換的定義、數值化實現方法及其應用。重點比較了三種數值化實現方法的優缺點，詳細闡釋了離散采樣型數值化方法的實現過程。此外，本文對分數階Fourier變換在數字水印、信號檢測與參數估計和生理信號去噪等信號處理中的應用做了概述，系統闡釋其算法原理與處理過程。最后，總結了分數階Fourier變換在時變、非平穩等復雜信號處理中表現出的優勢，并展望了今后的研究發展方向。

分數階Fourier變換（FrFT）；數值化實現；數字水印；信號檢測與參數估計；生理信號去噪

分數階Fourier變換（Fractional Fourier Transform，FrFT）因其具有許多傳統Fourier變換不具備的性質受到眾多研究人員的關注，在很多科學研究和工程技術領域均有應用，如量子力學［1-4］、光學系統和光信號處理［5，6］、光圖像處理［7-9］等。FrFT之所以首先在光信號處理中得到了應用，是因為光學實現相對比較容易，而直到20世紀90年代中期，由于提出了多種分數階Fourier變換的離散化方法及其快速實現算法，才使得FrFT真正在電信號處理領域中體現出其應用價值［10-12］。

FrFT作為一種新的信號分析工具，在信號處理領域中具有非常廣泛的應用前景。近幾年，新的研究成果也不斷涌現。從處理方法的角度來分析，目前國內外對FrFT的應用研究主要圍繞以下幾種思想：

（1）利用FrFT的聚焦性。直接將傳統Fourier變換的某些理論和應用推廣到分數階Fourier變換域。傳統的Fourier變換通常用于平穩信號的分析與處理，對于非平穩信號、時變信號的分析處理能力則失效，而FrFT對該類信號表現出良好的分析能力。傳統Fourier變換可以理解為信號在一組完備正交的正弦基上的展開，因此正弦信號的Fourier變換是一個沖激函數；FrFT則可以理解為信號是在一組正交的Chirp基上的展開，相應地，Chirp信號在某個特定階次的FrFT也是一個沖激函數，我們稱其為聚焦性。聚焦性對分析和處理Chirp類信號是十分有利的，其直接應用就是對Chirp信號進行檢測和參數估計。正是由于Chirp信號廣泛應用于通信、聲納、生物醫學等領域中，尤其是現代雷達系統，因此基于FrFT的分析與處理算法被用于雷達信號處理中的多目標檢測與跟蹤、SAR與ISAR成像、運動參數估計等技術中［13-17］。

（2）利用FrFT的時頻旋轉特性。一個信號的FrFT的Wigner分布是原信號Wigner分布的坐標旋轉形式。FrFT的這種時頻旋轉特性對于分析與處理非平穩信號是十分有利的。在實際工程應用中，有用信號的提取與噪聲的抑制是一項十分重要的課題。傳統濾波方法一般只限于頻域加窗或遮隔處理，但是當信號與噪聲之間存在較強的時頻耦合時，傳統的濾波器難以有效實現信噪分離。此時，利用FrFT將坐標軸旋轉到合適的角度，在新的分數階Fourier變換域上解除信號與噪聲之間的耦合，可實現噪聲的完全濾除和信號的無失真恢復。這就是分數階Fourier域濾波的基本原理［18-22］。

（3）利用FrFT與短時Fourier變換、小波變換、Wigner分布、Radon-Wigner變換等時頻分析工具的內在聯系，改進了一些非平穩信號的處理方法，并進一步擴展了FrFT的應用領域。如Radon-Wigner變換經常用于分析各種時變信號，而FrFT與Radon-Wigner變換之間的關系表明：信號FrFT后的模平方恰好是該方向上的Radon-Wigner變換。基于這一關系，Radon-Wigner變換的許多研究成果均可以直接應用到FrFT中。此外，在某些場合，用FrFT來替代其他的時頻變換還可以帶來一些優勢，如FrFT可以借助FFT實現，計算方法較為簡便；另一方面，FrFT是一種一維線性變換，在多分量信號情況下，可以有效地避免交叉項的干擾［18，23］。

本文從分數階Fourier變換的定義、離散化方法及其應用三個層面對分數階Fourier變換的理論體系進行闡述。具體內容如下：首先，介紹了分數階Fourier變換的定義；然后，闡述了分數階Fourier變換的離散化算法，對各種離散化方法進行了對比，重點分析了離散采樣型分數階Fourier變換的計算方式；其次介紹了分數階Fourier變換在信號處理中的應用，包括數字水印、信號檢測與參數估計、生理信號去噪；最后，對全文進行總結，對今后的研究方向進行了展望。

1　分數階Fourier變換定義

分數階Fourier變換又稱為角度Fourier變換（AFT）或者旋轉Fourier變換（RFT），其函數x（t）的FrFT定義如下［24］：

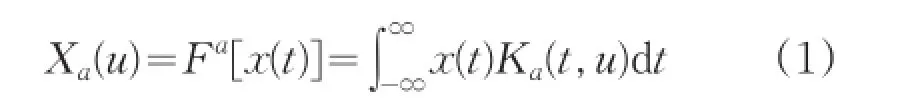
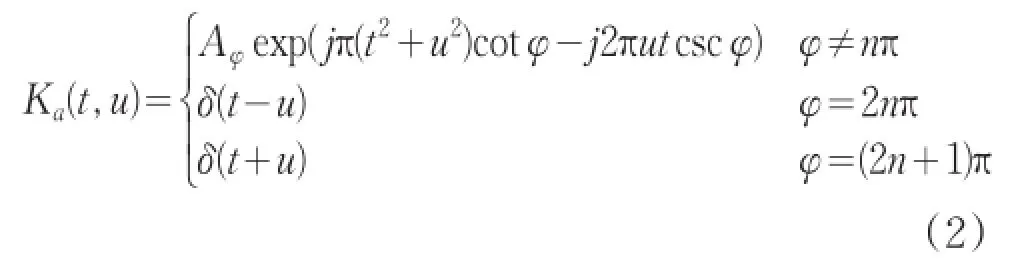
根據式（1）和式（2），FrFT的定義式改寫為：

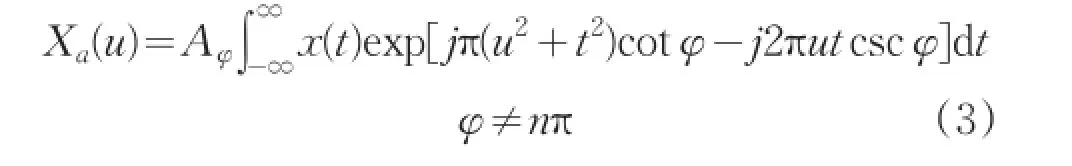
2　分數階Fourier變換離散化

FrFT自誕生以來，憑借自身的優勢和廣闊的應用潛力在各個領域中受到廣泛的關注，如同快速傅里葉變換（Fast Fourier Transform，FFT）大力推動了Fourier變換理論飛速發展一樣，為了在實際工程中能夠實現分數階Fourier算子、濾波器、相關器以及其他系統的應用，需要對FrFT進行數值化實現［24，25］。為了便于計算機處理，必須對輸入信號和FrFT的核函數進行離散化處理，從FrFT的基本定義可看出其離散化計算比DFT復雜的多，因此，一種高效精確的FrFT離散化和快速算法是工程應用中急需解決的問題。

為了確保離散化分數階Fourier變換（DFRFT）在基本概念上的縝密性，每個真正“嚴格”的形式都需符合以下性質［26-30］：（1）旋轉相加性；（2）酉性；（3）當變換階次為1時，退化為DFT；（4）變換階次的連續性；（5）近似連續分數階傅里葉變換；（6）具有快速算法；（7）有閉合表達式。國內外學者提出的許多離散方法中沒有一種方法能夠同時滿足上述所有要求。目前，主要有三種比較可行的離散化方法［31-33］：離散釆樣型、特征分解型、線性加權型。表1給出了這三種DFRFT的對比結果。

表1　三種DFRFT的對比結果

目前已有的各種DFRFT算法中，離散采樣型DFRFT與連續變換近似，其精度較高、計算復雜度低、運算量小并有閉合形式的表達式，因此廣泛應用于分數域非均勻釆樣與重構、chirp信號檢測和參數估計、分數域濾波等研究領域中，是目前應用最廣的數值計算方法之一。

該算法是由Ozaktas提出［34］，又被稱作分解法。由式（1）定義的連續FrFT出發，先將復雜的積分表達式進行分解，簡化為幾個簡單的計算，再通過離散化，最后得到其離散卷積的表達式，該離散卷積即可用FFT計算，因此本文主要介紹采樣型方法的實現。

另外，需要特別強調的是，必須對信號進行量綱歸一化［35］處理后才能對其進行FrFT數值計算，這一特殊技巧在離散化過程中起到了非常重要的作用。

量綱歸一化具體過程如下：

其中T表示信號的時寬，F表示信號的帶寬。則量綱歸一化坐標為：

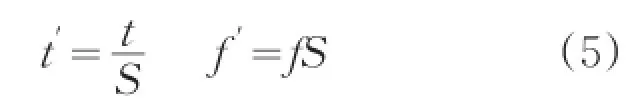
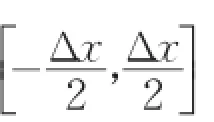
量綱歸一化后的信號可以進行采樣型DFRFT，具體步驟如下［36］：

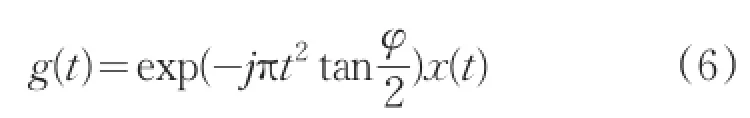
步驟2：g（t）與chirp信號exp（jπt2cscφ）做卷積，即

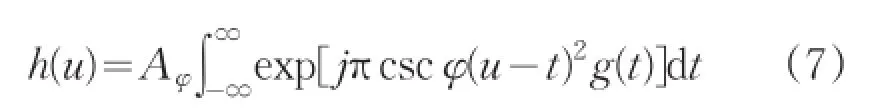
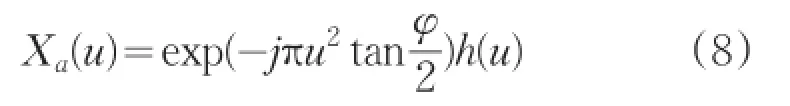
DFRFT可以借助FFT實現，其流程圖如圖1所示。

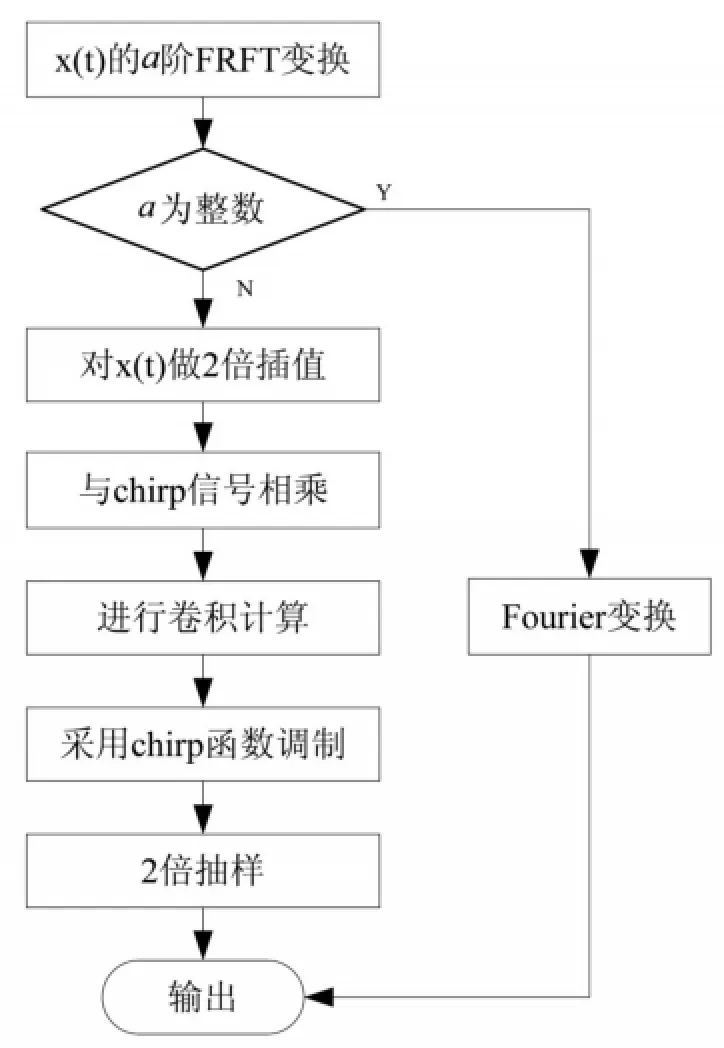
圖1　a階FrFT流程圖

3　FrFT在信號處理中的應用

3.1數字水印

近幾年，隨著互聯網的快速發展，越來越多的數字信息在網上被傳送和發布，相應地，信息竊取、信息詐騙等違法活動也日益猖獗。因此，信息安全領域迫切需要一種保密技術，可以有效地對數字信息進行保護，數字水印技術應運而生。

傳統數字水印方法可以分為空間域和變換域兩種水印算法，其中變換域方法較為常用，如離散余弦變換、離散傅里葉變換、離散小波變換等。這些方法加入水印后，當圖像進行幾何變形、旋轉、噪聲干擾、圖像壓縮和剪切等操作時，水印信息容易丟失，因此算法的魯棒性不高。2001年，Djurovic等人［37］首次將FrFT應用于數字水印，這種水印算法靈活性更高，其后又出現了一些改進算法［38-40］，進一步增強了數字水印的魯棒性。

3.1.1水印嵌入

首先，對大小為M×N的載體圖像I進行分塊，記作Ii，i=1，2，3…，對每塊圖像進行變換階次為（a1，a2）的二維FrFT，此階次作為數字水印的密鑰，變換后得到Ii的FrFT系數矩陣，將其按降序排列，記為變換系數Si，i=1，2，3…。

然后，產生一組偽隨機序列R，對待嵌入的水印圖像信息W（i，j）進行加密，加密后的水印信息記作Wˉ（i，j），其中=W+R。

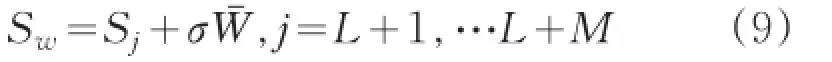
其中，Sj∈Si，σ表示水印嵌入的強度。

最后，將嵌入水印后的變換系數Sw重新排列為矩陣，并對其進行二維FrFT，其中變換階次為（-a1，-a2），得到的含水印的圖像記作Iw。水印嵌入過程如圖2所示。

3.1.2水印提取

水印提取與水印嵌入的過程正好相反，他們互為逆過程。對于存在疑問的圖像檢測其中是否含有水印信息的過程，稱為水印提取。首先對待檢測圖像Iw進行分塊，然后分別對其進行（a1，a2）階的二維FrFT，選擇原始水印的嵌入位置，利用原始圖像信息提取疊加信息W*：

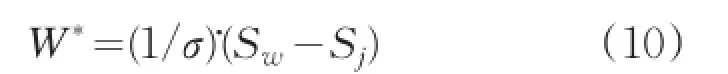
最后將疊加信號中的偽隨機序列R去除，得到水印信息W：

水印提取過程如圖3所示。

3.2信號檢測與參數估計

圖2　水印嵌入過程示意圖

圖3　水印提取過程示意圖

由于分數階Fourier變換可以解釋為Chirp基分解，因此分數階Fourier變換特別適合于處理Chirp類信號。在雷達、聲納等通信系統中常用的信號就是線性調頻（Chirp）信號，由于它在FrFT域中不同的階次呈現出不同的能量聚集性，如圖4所示，通過這一特性在FrFT域中進行峰值二維搜索，即可實現對Chirp信號的檢測和參數估計。

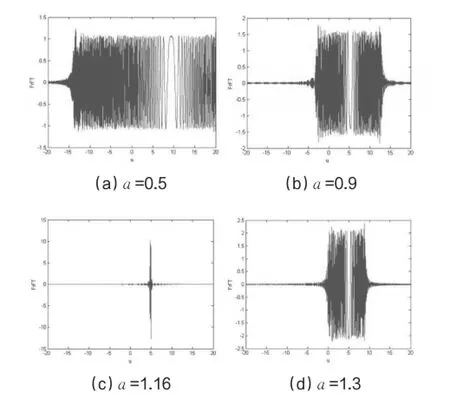
圖4　FrFT的能量聚集性

目前，對Chirp信號進行檢測和參數估計的大多數研究［41-45］均是基于這一思想，系統框圖如圖5所示。

圖5　Chirp信號參數估計系統框圖

設x（t）為待檢測的LMF信號，即

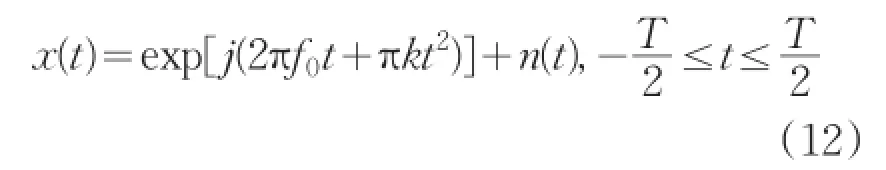
其中，f0表示信號的初始頻率，k表示信號的調頻率，n（t）表示高斯噪聲。

通過量綱歸一化后對其進行FrFT，得到其二維分布圖，如圖6所示。

圖6　FrFT的二維分布圖

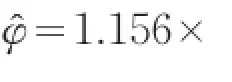
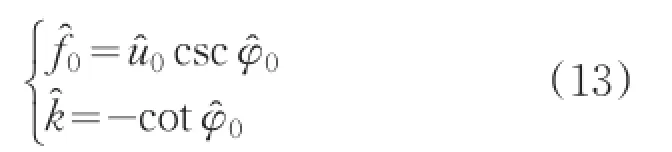
通過以上計算，可完成對Chirp信號的檢測和參數估計，在高斯噪聲背景下較低信噪比時，該方法仍然表現出十分好的檢測效果。

3.3生理信號去噪

生理信號屬于非平穩的低頻微弱信號，具有長相關特性，且與干擾信號存在較強的時頻耦合，如腦電信號［46，47］，心電信號［48］，肌電信號［49］等，這類隨機信號的波形和相位一方面受采集方式和環境的影響，另一方面，不同的采集對象所表現出的生理信號波形的特征也是不同的。

一般情況下，我們無法準確預測當前實現中的隨機信號在某一刻的取值，但是，隨機信號一般服從確定的概率分布和聯合概率分布。以心電信號為例，信號的取值具有確定的概率分布和概率密度函數。另外，經過多次實際觀察與統計，可以明確掌握心電信號具有哪些確定的統計特征量，這些統計特征量能夠反映信號的許多性質，這些性質正是評價心血管疾病，特別是心臟功能的重要依據。在生理信號中，一個噪聲點可能會導致某些疾病的誤判，因此，為了獲得清晰準確的生理信號波形，提高分析和診斷的精確性，必須對信號進行一定的分析和處理，使數據曲線更平滑，特征點更突出。

如果信號與噪聲在時間軸上的投影不存在重疊（如圖7（a）所示），那么可以在時域中采用合適的濾波器濾除噪聲；如果信號與噪聲在頻率軸投影不存在重疊（如圖7（b）所示），那么可以通過合適的濾波器在頻域中濾掉此時的干擾；但是當信號和干擾噪聲在時域和頻域中的投影均存在重疊，即存在時頻耦合（如圖7（c）所示），此時不可能只通過時域或頻域濾波完全濾除噪聲。但是，分數階Fourier變換可以將坐標旋轉到某一角度，解除時頻耦合，最大程度地濾除噪聲。也就是說，在某個角度的分數階Fourier域能夠得到更好的信號與噪聲分離效果。不僅如此，時域和頻域還可以看作是特殊情況下的分數階Fourier變換域，當變換階次a=0時，對應時域，當變換階次a=1時，對應頻域，如圖7所示。

因此，可以利用在分數階Fourier域中信號和噪聲分離的特點對生理信號進行FrFT，找到使信號與噪聲分離時的最佳旋轉角度，在此分數階Fourier域中進行濾波，然后再對其進行分數階Fourier逆變換，最后得到去噪信號，具體算法如圖8所示。

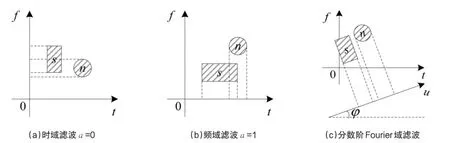
圖7　信號與噪聲的時頻分布圖

圖8　去噪算法框圖

通過上述的分析，該算法的具體步驟如下［50］：

（1）根據FrFT的對稱性，變換階次a∈［0，2），求輸入信號x（n）的FrFT；

（2）對變換后的信號進行二維搜索，找到最佳變換階次a′；

（3）計算信號x（n）在階次為a′時的FrFT；

（4）在最佳分數階Fourier變換域中進行濾波；

（5）對濾波后的信號進行分數階Fourier逆變換，即-a′階FrFT，得到時域輸出信號y（n）。

4　結語

本文對近年來分數階Fourier變換在數字水印、信號檢測與參數估計以及生理信號處理中的研究成果進行了總結，對分數階Fourier變換的理論體系做了系統的闡述。從分數階Fourier變換域與時域、頻域之間的關系可以看出，分數階Fourier變換實質上是一種統一的時頻變換，能夠同時反映出信號在時域、頻域的信息。通過本文介紹的幾種分數階Fourier變換在信號處理領域中的應用可以發現，它適于處理如Chirp類的非平穩信號，而且因為多了一個變換階次的自由參量，所以分數階Fourier變換在某些條件下往往能夠得到傳統時頻分布或Fourier變換所得不到的效果，由于其具有比較成熟的快速離散化算法，在得到更好效果的同時并不需要付出太多的計算代價，因此具有十分廣闊的工程應用前景。

至今為止，有關分數階Fourier變換在信號處理中的應用研究已經取得了豐碩成果，但是仍然存在許多理論和工程上的問題需要解決。如在數字水印中，分數階Fourier變換體現出較為理想的魯棒性，因此應將分數階Fourier變換推廣到圖像邊緣檢測、圖像增強、模式識別等領域，拓寬其在圖像處理中的應用范圍，提高圖像處理的質量；在Chirp信號的參數估計方面，在高斯噪聲背景下FrFT表現出良好的估計效果，然而如何處理更加復雜的噪聲，如非均勻噪聲、有色噪聲、非高斯噪聲等情況，都是未來的研究和發展方向；在處理如生理信號這類非平穩信號時，通過分數階Fourier變換可以將信號與噪聲進行分離，但是非平穩信號是一個龐大而復雜的研究領域，不僅需要先進的理論支持，還涉及到多個交叉學科，在這一領域仍有很多問題有待進一步研究。因此不僅要拓寬分數階Fourier變換在信號處理領域中的應用，如在聲信號、通信信號、生物醫學、神經網絡等方面的應用，還應對其加以改進，與其他的信號處理技術相結合，形成優勢互補的新技術，為解決非高斯、非平穩、非因果等“非”的問題提出解決方案。

［1］Namias V.The fractional order Fourier transform and its application to quantum mechanics［J］.IMA JournalofAppliedMathematics，1980，25（3）：241-265.

［2］MendlovicD，OzaktasHM.FractionalFourier transformsandtheiropticalimplementation：I［J］. JOSA A，1993，10（9）：1875-1881.

［3］OzaktasHM，MendlovicD.FractionalFouriertransforms and their optical implementation.II［J］. JOSA A，1993，10（12）：2522-2531.

［4］Cai L Z，Wang Y Q.Optical implementation of scale invariant fractional Fourier transform of continuously variable orders with a two-lens system［J］. Optics&Laser Technology，2002，34（3）：249-252.

［5］Bernardo L M，Soares O D D.Fractional Fourier transforms and optical systems［J］.Optics Communications，1994，110（5）：517-522.

［6］Ozaktas H M，Aytür O.Fractional Fourier domains ［J］.Signal Processing，1995，46（1）：119-124.

［7］Bernardo L M，Soares O D D.Fractional Fourier transforms and imaging［J］.JOSA A，1994，11（10）：2622-2626.

［8］ Lohmann A W.Image rotation，Wigner rotation，and the fractional Fourier transform［J］.JOSA A，1993，10（10）：2181-2186.

［9］ Liu S，Ren H，Zhang J，et al.Image-scaling problem in the optical fractional Fourier transform［J］. Applied optics，1997，36（23）：5671-5674.

［10］Saxena R，Singh K.Fractional Fourier transform：A novel tool for signal processing［J］.Journal of the Indian Institute of Science，2013，85（1）：11.

［11］ Ozaktas H M，Zalevsky Z，Kutay M A.The fractionalFouriertransform［M］.Wiley，Chichester，2001.

［12］Tao R，Deng B，Wang Y.Research progress of the fractional Fourier transform in signal processing ［J］.Science in China Series F，2006，49（1）：1-25.

［13］ 殷敬偉，惠俊英，蔡平等.基于分數階 Fourier變換的水聲信道參數估計［J］.系統工程與電子技術，2007，29（10）：1624-1627.

［14］Wang Q，Pepin M，Beach R J，et al.SAR-based vibrationestimationusingthediscretefractional Fouriertransform［J］.GeoscienceandRemote Sensing，IEEETransactionson，2012，50（10）：4145-4156.

［15］ Guan J，Chen X L，Huang Y，et al.Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter［J］.IET Radar，Sonar&Navigation，2012，6（5）：389-401.

［16］Liu Y，Wang X S.The analysis of the effect for a micro-motion jamming to multi-aperture SAR/ GMTI base on fractional Fourier transform［J］.Dianzi Xuebao（Acta Electronica Sinica），2011，39（9）：2039-2045.

［17］Sun H B，Liu G S，Gu H，et al.Application of the fractional Fourier transform to moving target detection in airborne SAR［J］.Aerospace and Electronic Systems，IEEE Transactions on，2002，38（4）：1416-1424.

［18］Yu J，Liu K，Huang X，et al.A novel fractional Fourier domain filter design based on time-frequency image edge detection［C］.The Proceedings of the Second International Conference on Communications， SignalProcessing， andSystems. Springer International Publishing，2014：213-223.

［19］Ran T，Siyong Z，Yue W.Adaptive time-varying filter for linear FM signal in fractional Fourier domain［C］.6thIEEEInternationalConferenceon Signal Processing，2002，2：1425-1428.

［20］Elgamel S A，Soraghan J J.Enhanced monopulse radar tracking using filtering in fractional Fourier domain［C］.2010IEEEonRadarConference. 2010：247-250.

［21］Elgamel S A，Soraghan J J.Using EMD-FrFT filtering to mitigate very high power interference in chirp tracking radars［J］.Signal Processing Letters，IEEE，2011，18（4）：263-266.

［22］Zhai M Y.Seismic data denoising based on the fractional Fourier transformation［J］.Journal of Applied Geophysics，2014，109：62-70.

［23］ Han J，Wang Q，Qin K.The non-stationary signal oftime-frequencyanalysisbasedonfractional FouriertransformandWigner-Houghtransform ［M］.Mechatronics and Automatic Control Systems. Springer International Publishing，2014.

［24］Sejdi E，Djurovi I，Stankovi L J.Fractional Fourier transform as a signal processing tool：an overview of recent developments［J］.Signal Processing，2011，91（6）：1351-1369.

［25］Marinho F J，Bernardo L M.Numerical calculation offractionalFouriertransformswithasingle fast-Fourier-transformalgorithm［J］.JOSAA，1998，15（8）：2111-2116.

［26］Shi J，Sha X，Song X，et al.Generalized convolutiontheoremassociatedwithfractionalFourier transform［J］.Wireless Communications and Mobile Computing，2014，14（13）：1340-1351.

［27］AlmeidaLB.ThefractionalFouriertransform and time-frequency representations［J］.Signal Processing，IEEETransactionson，1994，42（11）：3084-3091.

［28］Almeida L B.Product and convolution theorems for the fractional Fourier transform［J］.Signal Processing Letters，IEEE，1997，4（1）：15-17.

［29］Pei S C，Ding J J.Closed-form discrete fractional and affine Fourier transforms［J］.Signal Processing，IEEE Transactions on，2000，48（5）：1338-1353.

［30］Candan C，Kutay M A，Ozaktas H M.The discrete fractional Fourier transform［J］.Signal Processing，IEEETransactionson，2000，48（5）：1329-1337.

［31］Pei S C，Yeh M H.Two dimensional discrete fractional Fourier transform［J］.Signal Processing，1998，67（1）：99-108.

［32］ Dickinson B W，Steiglitz K.Eigenvectors and functions of the discrete Fourier transform［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1982，30（1）：25-31.

［33］ Pei S C，Yeh M H，Tseng C C.Discrete fractional Fourier transform based on orthogonal projections［J］.Signal Processing，IEEE Transactions on，1999，47（5）：1335-1348.

［34］ Ozaktas H M，Arikan O，Kutay M A，et al.Digital computation of the fractional Fourier transform［J］. IEEE Transactions on signal processing，1996，44 （9）：2141-2150.

［35］ 劉鋒，徐會法，陶然.分數階Fourier變換中量綱歸一化因子的選取［J］.系統工程與電子技術，2011，33（2）：237-241.

［36］ 黃宇，劉鋒，王澤眾，等.基于周期FRFT的LFMCW信號檢測與參數估計［J］.中國科學：信息科學，2014，4：007.

［37］ Djurovic I，Stankovic S，Pitas I.Digital watermarking in the fractional Fourier transformation domain ［J］.Journal of Network and Computer Applications，2001，24（2）：167-173.

［38］Yu F Q，Zhang Z K，Xu M H.A digital watermarkingalgorithmforimagebasedonfractional Fourier transform［C］.1ST IEEE Conference on Industrial Electronics and Applications，2006：1-5.

［39］FengZ，XiaominM，ShouyiY.Multiple-chirp typed blind watermarking algorithm based on fractional Fourier transform［C］.Intelligent Signal Processing and Communication Systems，2005：141-144.

［40］Rawat S，Raman B.A blind watermarking algorithm based on fractional Fourier transform and visual cryptography［J］.Signal Processing，2012，92 （6）：1480-1491.

［41］ 徐會法，劉鋒，張鑫.分數階Fourier域強弱LFM信號檢測與參數估計［J］.信號處理，2011，27（7）：1063-1068.

［42］ 唐江，趙擁軍，朱健東，等.基于FrFT的偽碼-線性調頻信號參數估計算法［J］.信號處理，2012，28（9）：1271-1277.

［43］ 朱健東，趙擁軍，唐江.線性調頻連續波信號的周期分數階 Fourier變換檢測與估計［J］.電子與信息學報，2013，35（8）：1827-1833.

［44］ Liu F，Xu H F，Tao R，et al.Research on resolution between multi-component LFM signals in the fractional Fourier domain［J］.Science China Information Sciences，2012，55（6）：1301-1312.

［45］ Wang J Z，Su S Y，Chen Z P.Parameter estimation of chirp signal under low SNR［J］.Science China Information Sciences，2015，58（2）：1-13.

［46］Guerrero-MosqueraC，VerleysenM，VazquezA N.EEG feature selection using mutual information and support vector machine：A comparative analysis ［C］.2010 Annual International Conference of the IEEE on Engineering in Medicine and Biology Society（EMBC），2010：4946-4949.

［47］ Khalid M B，Rao N I，Rizwan-i-Haque I，et al.A BrainComputerInterface（BCI） usingfractional Fourier transform with time domain normalization and heuristic weight adjustment［C］.9th IEEE International Conference on.Signal Processing，2008：2734-2737.

［48］Krishna B T.Electrocardiogram signal and linear time-frequency transforms［J］.Journal of The Institution of Engineers（India）：Series B，2014，95 （4）：377-382.

［49］Delk K K，Gevirtz R，Hicks D A，et al.The effectsofbiofeedbackassistedbreathingretraining on lung functions in patients with cystic fibrosis ［J］.CHEST Journal，1994，105（1）：23-28.

［50］ 徐婷.分數階Fourier變換在心電信號處理中的應用研究［D］.西安工業大學，2012.

An Overview of Applied Research for Fractional Fourier Transform in Signal Processing

WANG Chunyang，LIU Xuelian
（School of Electronics and Information Engineering，Changchun University of Science and Technology，Changchun 130022）

In this paper，we provide an overview of the definition，digital realizations and applications of the Fractional Fourier transform.Specifically，the paper discusses various approaches for digital realizations of the FrFT and compares their advantages and disadvantages，and then，explains the implementation procedure of DFRFT through sampling of FrFT in detail.Furthermore，the paper introduces the applications of FrFT in digital watermarking signal detection and parameter estimation，physiological signal denoising，and illuminates systematically their algorithm principles and processing procedures.Finally，the paper summarizes the advantages of the fractional Fourier transform in non-stationary and time-varying complex signal processing，and looks ahead to the research and development directions in the future.

fractional Fourier transform（FrFT）；digital realizations；digital watermarking；signal detection and parameter estimation；physiological signal denoising

TN911

A

1672-9870（2015）05-0001-08

2015-10-12

王春陽（1964-），女，博士，教授，E-mail：wangchunyang19@cust.edu.cn