彈性輪與地面相互作用建模及仿真
王金龍,李杰
(1.長春理工大學 機電工程學院,長春 130022;2.吉林大學 汽車工程學院,長春 130025)
彈性輪與地面相互作用建模及仿真
王金龍1,李杰2
(1.長春理工大學 機電工程學院,長春 130022;2.吉林大學 汽車工程學院,長春 130025)
以半經(jīng)驗法為指導思想,應(yīng)用彈性輪與地面相互作用的假設(shè)模型,建立了彈性輪所受地面推力和阻力的顯式解和數(shù)值解的求解方法。選擇有代表性的指標來評價通過性能。應(yīng)用面向?qū)ο蟮腣C++語言編制出仿真分析軟件,仿真結(jié)果與試驗結(jié)果趨勢一致。并以胎壓為例分析了車輪和地面參數(shù)對結(jié)果的影響。
彈性輪;地面;相互作用;建模仿真
汽車在地面上行駛時,是通過車輪與地面的相互作用產(chǎn)生滾動阻力和牽引力的。研究車輪與地面的相互作用有剛性輪假設(shè)和彈性輪假設(shè),其中彈性輪假設(shè)更為接近實際。研究彈性輪與地面相互作用的主要任務(wù)是用理論分析和試驗方法建立彈性輪與地面相互作用的模型,揭示彈性輪在各種地面的工作狀態(tài),確定輪胎或車輛的設(shè)計參數(shù)以及選擇最佳設(shè)計方案,以達到在不同地面條件下合理使用汽車和改進現(xiàn)有車輛性能的目的[1,2]。
彈性輪與地面作用時,輪胎和地面都發(fā)生變形,所以要用理論分析的方法預測輪胎的外形是非常困難的,這就要用到一些簡化假設(shè)。為了分析問題和解決問題的方便,考慮到輪胎和地面的變形,假設(shè)彈性輪在地面上滾動時通常都形成有一定深度的輪轍,而與此同時輪胎本身像在此深度處的假想硬路面上變形一樣,即輪胎與地面作用的接觸面由從輪胎側(cè)面看為底部的平直段和前部的圓弧段組成【3】。
1 彈性輪與地面相互作用建模
1.1彈性輪與地面相互作用的幾何關(guān)系
彈性輪與地面相互作用模型是在剛性輪基礎(chǔ)上建立的。當充氣輪胎的充氣壓力與胎體剛度產(chǎn)生的壓力之和小于地面對剛性輪胎圓周最低點的支承壓力時,應(yīng)用彈性輪模型。彈性輪與地面相互作用的幾何關(guān)系如圖1所示。
圖1中,AB段為輪胎壓過的地面,彈性輪壓扁部分的長度是lt,并且關(guān)于中心線對稱。BC段為輪胎與地面作用的圓弧部分,lt1為其向水平投影的長度。CD段為未作用地面。δt為輪胎垂直變形,z為作用接觸線上某點到未作用地面的垂直距離,z0為最大下陷量。x為BC段圓周上某點的水平坐標,以輪胎的中心線為基準,向右為正。θ為圓周上某點與豎直坐標軸的夾角,θB、θC分別為圓弧段兩端與豎直坐標軸的夾角。W為車輪的垂直載荷,r為車輪半徑。

圖1 彈性輪與地面相互作用幾何關(guān)系圖
1.2彈性輪與地面相互作用的受力分析
1.2.1彈性輪的地面阻力
要得到車輪的地面推力和阻力,先要求取彈性輪的垂直變形和最大沉陷。輪胎氣壓與胎體剛度產(chǎn)生的壓力之和為輪胎被壓扁處的地面壓力,為最大沉陷量z0的函數(shù),即

在垂直方向,車輪的載荷


由圖1可知,當沉陷量z0較小時(z0≤r/3),可近似表示為:

并令t2=z0-z+δt,則得

式(3)就可以轉(zhuǎn)化為:
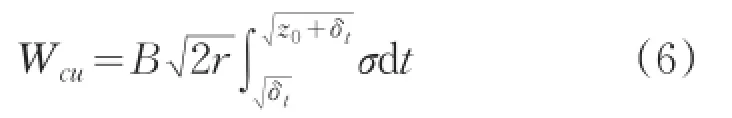
根據(jù)承壓特性模型

由z與t的關(guān)系代入(6)式,最后匯總到(2)式,可得垂直載荷為輪胎變形δt的一元函數(shù)。采用小步長逐次接近法可計算出比較精確的輪胎變形的數(shù)值解。
彈性輪的壓實阻力根據(jù)圖1可得

代入承壓特性模型應(yīng)力公式即可求得。
在求得最大沉陷量后,彈性輪即可應(yīng)用與剛性輪同樣的方法,代入承載特性模型

式中,q0單位面積的極限承載應(yīng)力;Q0地基垂直向的極限載荷;q=γD基礎(chǔ)兩側(cè)土的超載;A、B、D基礎(chǔ)的作用面積、寬度、埋置深度;γ、c土的容重、凝聚力;Nc、Nq、Nγ地面承載系數(shù)。求出其推移阻力

輪胎變形引起彈滯損耗將構(gòu)成彈性輪的彈滯阻力Frt,這是彈性輪與剛性輪的主要區(qū)別。其值只與輪胎本身的參數(shù)及胎壓有關(guān),而與地面參數(shù)無關(guān),可由試驗近似地確定。Bekker采用下述公式確定彈滯阻力:

式中,ft表示單位負荷彈滯損耗阻力,簡稱輪胎變形阻力系數(shù)。在實際應(yīng)用中,根據(jù)試驗確定 ft時,ft可用下述公式表示:

式中,u、a為與輪胎有關(guān)的經(jīng)驗系數(shù)。為了確定u 和a值,必須在給定工作載荷W情況下,以不同的胎壓使輪胎在水平硬路面(水泥路面)上滾動。這樣測出的滾動阻力系數(shù) fti,可假定主要是由胎體變形的彈滯損耗所引起的。由試驗確定的 fti-pi曲線,稱為輪胎變形阻力系數(shù)的標準曲線,根據(jù)該曲線可以用最小二乘法確定u和a。
1.2.2彈性輪的地面推力
對整個車輪與地面相互作用接觸面上的剪切應(yīng)力的水平分量積分即得彈性輪的地面推力[1,2,7]:

根據(jù)彈性輪的地面推力的積分表達式(13)可知,彈性輪的地面推力在具體計算時,要分為被壓扁的水平部分和與地面被推起的前緣接觸的圓周部分。
水平部分,由于τ(θ)為水平方向,所以只需對τ(θ)在x方向上積分即可,這一部分類似于履帶的地面推力,其地面推力可表示為:

水平部分的剪切位移可根據(jù)履帶剪切位移的公式 j=srX求得,其中sr為滑轉(zhuǎn)率。由于水平段沉陷量一致,所以壓力不變,即σ=σ0=f(z0)。代入地面剪切特性模型
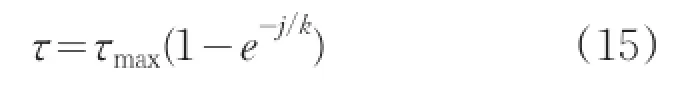
即可求出這一段的地面推力。
圓周部分的推力計算的角度積分限為θB到θC,即

因此,只要承壓模型及剪切模型確定后,就可以根據(jù)式(16),利用數(shù)值積分方法求得彈性輪與地面作用圓周段的地面推力。在進行數(shù)值積分時,需要對承壓模型及剪切模型進行坐標轉(zhuǎn)換,即利用關(guān)系式z=r(cosθ-cosθC),把XZ方向坐標轉(zhuǎn)換為旋轉(zhuǎn)坐標,然后再對角度進行數(shù)值積分以求得結(jié)果。
車輛所具有的牽引力為驅(qū)動力與阻力之差,即

式中FDP為牽引力,稱為掛鉤牽引力。
1.3評價指標
為了綜合衡量車輛與地面的相互作用,國內(nèi)外的眾多學者都從不同的角度提出了不同的評價指標。綜合來看,國內(nèi)外學者共同認可的系數(shù)有兩個:一是牽引系數(shù),一是效率系數(shù)。牽引系數(shù)是車輪的掛鉤牽引力與車輪載荷之比,其值越大,儲備的“凈推力”就越多,行駛也就越順利。效率系數(shù)反映了車輪將輸入的功率轉(zhuǎn)化為有用功率的比率,其表達式如下:

式中,TE—效率系數(shù);V—車輪實際行駛速度;M—彈性驅(qū)動輪的扭矩;ω—彈性驅(qū)動輪的角速度。效率系數(shù)越大,輸出的功率所占的比重就越大,用來克服阻力所占的功率就越小。因此,效率系數(shù)越大,能量的利用率越高,經(jīng)濟性也越好[5,6]。
考慮到彈性輪與地面相互作用的特點,本文建議兩個作為評價車輛通過性的補充指標:彈性輪最大相對徑向變形和彈性輪最大相對徑向沉陷。彈性輪與剛性輪的主要區(qū)別在于彈性輪與地面相互作用時,輪胎要發(fā)生變形。在地面條件和車輛條件不變的情況下,車輪的載荷越大,輪胎的變形越明顯。但輪胎的變形不是無限制的,它要有一個上限來保證輪胎的正常工作而不損壞。考慮到不同的車型、不同直徑的車輪,引入彈性輪最大相對徑向變形δtr,即

式中,δt為彈性輪胎在豎直方向上的變形;r為輪胎半徑。實際使用中,δtr要小于它的最大值δtrmax,以保證輪胎的正常工作。無論是彈性輪還是剛性輪,當與地面相互作用時,都會使地面產(chǎn)生沉陷。如果車輪下陷到一定程度,就會造成車輪阻力過大,而無法通過該地段。對于彈性輪的沉陷,還要把輪胎變形考慮進去。因為由圖(1)可見,彈性輪與地面作用的最大沉陷量雖然為z0,但如果當作剛性輪考慮,其沉陷還包括輪胎的變形部分,在未壓實地面以上到車軸的長度與半徑比越小,即沉陷的部分越多,車輪的阻力就越大,越不容易通過該段路面。為反映這種狀況,同時考慮到不同車型、不同車輪,引入彈性輪最大相對徑向理想沉陷,即

式中,z0r—彈性輪最大相對沉陷;z0—彈性輪的實際沉陷;r—輪胎半徑。δt—輪胎垂直變形。
2 仿真結(jié)果的驗證和影響參數(shù)分析
采用面向?qū)ο蟮腣C++語言開發(fā)出分析軟件,界面如圖2所示。模擬仿真采用表1中所示的基本參數(shù)進行,其它參數(shù)從略。

2 彈性輪與地面相互作用仿真軟件界面

表1 軟件仿真的基本參數(shù)
文獻[7]中給出了彈性輪胎在此基本參數(shù)下,三種不同輪胎氣壓時的牽引系數(shù)及效率系數(shù)的實際數(shù)據(jù)點,與本文仿真曲線的對比如圖3和圖4所示。
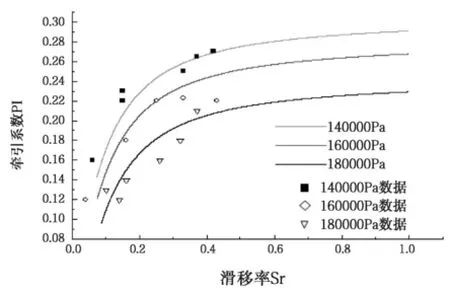
圖3 牽引系數(shù)曲線與實驗數(shù)據(jù)對比

圖4 效率系數(shù)曲線與實驗數(shù)據(jù)對比
圖3和圖4中的三條曲線分別表示胎壓為140000Pa、160000Pa和180000Pa時的牽引系數(shù)和效率系數(shù),橫坐標代表輪胎的滑移率。與測算得出的實驗點相比,數(shù)據(jù)符合較好,誤差較小,仿真具有很高的可信度。
圖3和圖4中還可以看出,隨著胎壓的增加,牽引系數(shù)和效率系數(shù)都有所下降,這是由于胎壓的增加導致阻力增加,如表2所示。

表2 充氣壓力變化時輪胎阻力和變形
同時,輪胎隨著氣壓的增大,變形減小、沉陷增加,越來越接近于剛性輪的特征。
通過對輪胎變形和阻力的影響,充氣壓力進而影響到地面推力和評價指標。在充氣壓力為140000Pa時,得到的地面推力如表3所示。從表中可以看出,在此充氣壓力下,輪胎的地面推力在滑移率比較小時,圓周段所提供的推力比平直段的大;滑移率超過0.2時,平直段所提供的推力就成為主要部分。

表3 充氣壓力為140000Pa時的地面推力
如果充氣壓力發(fā)生變化增加到180000Pa時,地面推力就會產(chǎn)生比較大的變化,表4的地面推力數(shù)據(jù)正體現(xiàn)了這種變化。
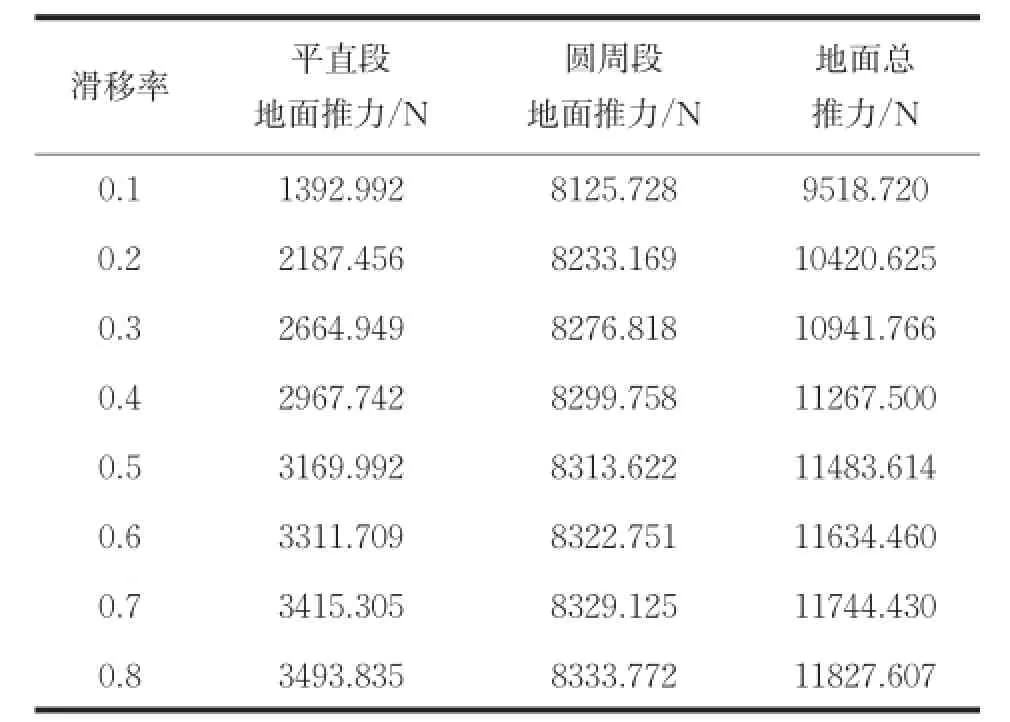
表4 充氣壓力為180000Pa時的地面推力
其它如車輪載荷、車輪幾何參數(shù)和地面參數(shù)變化對牽引通過性能的影響也可用相同的方法比較出來,在此就不贅述。因此,可應(yīng)用本軟件進行彈性輪與地面作用的分析并可輔助車輛的設(shè)計。
3 結(jié)論
(1)建立了彈性輪與地面相互作用模型,分析了彈性輪的受力狀況。
(2)在原有牽引系數(shù)和效率系數(shù)評價指標的基礎(chǔ)上,根據(jù)彈性輪的特點引入彈性輪最大相對徑向變形和彈性輪最大相對徑向理想沉陷兩個指標評價彈性輪的通過性。
(3)利用VC++語言開發(fā)了仿真分析軟件,仿真結(jié)果與實驗數(shù)據(jù)符合較好。以輪胎壓力變化為例分析了參數(shù)變化對牽引通過性能的影響。軟件可用來進行彈性輪與地面作用分析及輔助車輛設(shè)計。
[1] M G貝克.地面—車輛系統(tǒng)導論[M].北京:機械工業(yè)出版社,1978.
[2] 莊繼德.汽車通過性[M].長春:吉林人民出版社,1980.
[4] 余志生.汽車理論[M].北京:機械工業(yè)出版社,1981.
[5] 李幼德.汽車通過松軟地面的性能評價方法研究[D].長春:吉林工業(yè)大學,1981.
[5] 黃祖永.地面車輛原理[M].北京:機械工業(yè)出版社,1985.
[6] 張加才.沙漠車通過性及輪胎最佳充氣壓力的研究[D].長春:吉林工業(yè)大學,1993.
[7] 李杰,莊繼德,魏東,等.沙漠仿生輪胎與普通輪胎牽引性能的對比試驗[J].吉林大學學報:自然科學版,2006 (4):206-213.
The Research of Modeling and Simulation on Interaction Between Elastic Tire and Terrain
WANG Jinlong1,LI Jie2
(1.School of Mechatronical Engineering,Changchun University of Science and Technology,Changchun 130022;2.Automotive Engineering College,Jilin University,Changchun 130025)
Based on the semi-experience method,this paper applied forward model and hypothesis about interaction between elastic tire and terrain.Meanwhile,built some direct and indirect equations about driving force and resistance. Some typical evaluation-criterions were chosen to evaluate traffic ability.What’s more,the program for simulation was developed with Visual C++and the result of simulation was consistent to the result of test.This paper also analyzed influence of parameters of wheel and terrain by giving an example of tire pressure.
elastic tire;terrain;interaction;modeling and simulation
U461.54
A
1672-9870(2015)05-0080-04
2015-07-05
長春理工大學博士科研啟動基金(40301-834)
王金龍(1976-),男,博士,講師,E-mail:wjl19760819@163.com

