基于高斯混合模型的音樂情緒四分類研究

陸陽，郭濱，白雪梅

（長春理工大學(xué)　電子信息工程學(xué)院，長春　130022）

基于高斯混合模型的音樂情緒四分類研究

陸陽，郭濱，白雪梅

（長春理工大學(xué)電子信息工程學(xué)院，長春130022）

針對音樂情感復(fù)雜難以歸類的問題，提出了一種在四分類坐標(biāo)下建立高斯混合模型進(jìn)行音樂信號歸類的研究方法。在建立模型的基礎(chǔ)上，創(chuàng)新地為表示情緒特性的軸兩端建立模型使其轉(zhuǎn)換成二層分類器進(jìn)行加權(quán)判別。結(jié)果表明，為表示情緒特性的軸建立模型且權(quán)值分配在0.7和0.3的條件下，音樂的分類工作可以取得最優(yōu)結(jié)果，其結(jié)果明顯優(yōu)于直接為每類情緒建立模型的結(jié)果。

高斯混合模型；音樂情緒分類；加權(quán)判決

隨著計算機(jī)網(wǎng)絡(luò)等一系列新興媒體的到來，音樂逐漸滲透到我們?nèi)粘Ｉ钪械母鱾€角落。所以在海量信息的環(huán)境下，人們迫切需要對音樂信號進(jìn)行有效的識別和管理。但是由于音樂信號的旋律多變性，頻率復(fù)雜性等特點，使我們無法準(zhǔn)確地描述一首音樂到底屬于哪種類別。針對這種情況，結(jié)合前人研究的成果，本文對音樂信號進(jìn)行簡單的四分類研究，并進(jìn)行了兩種判別方法的比較。

本文使用的四分類模型圖如圖1所示，根據(jù)Thayer模型［1］轉(zhuǎn)換而來。圖中，縱軸代表音樂情緒能量和強(qiáng)烈的程度的指標(biāo)（Arousal），橫軸代表音樂情緒的正面或負(fù)面的指標(biāo)（Valence）［1］，由此形成了簡單的四分類坐標(biāo)系。如圖所示，把音樂信號歸為平靜、悲傷、激動、愉快四種典型的音樂情緒風(fēng)格。在此分類模型下，再進(jìn)一步使用高斯混合模型實現(xiàn)音樂的歸類。

圖1　音樂情緒四分類模型圖

1　高斯混合模型及EM算法

1.1高斯混合模型簡介

高斯混合模型（Gaussian mixture model，GMM）是一種經(jīng)常被用來描述混合密度分布的模型，即多個高斯分布的混合分布模型。在處理分類問題時，它能簡單而有效地體現(xiàn)同一類內(nèi)數(shù)據(jù)在特征空間中的分布特點，即同一類內(nèi)的數(shù)據(jù)在特征空間中的分布既具有分散性又具有聚合性［2］。所謂聚類，就是按照一定的標(biāo)準(zhǔn)將事物進(jìn)行區(qū)分和分類的過程。這一過程可以是無監(jiān)督的，即在此過程中沒有任何關(guān)于分類的先驗知識，僅僅靠事物之間的相似性作為劃分類的標(biāo)準(zhǔn)。聚類分析則指的是用數(shù)學(xué)的方法研究和處理給定對象的分類問題，它是一個將數(shù)據(jù)集劃分為若干聚合類的過程，它將相似度較高的數(shù)據(jù)對象劃分為一類，而將相似度較低的數(shù)據(jù)對象區(qū)分成其他類。

高斯混合模型是由單一高斯概率密度函數(shù)引申而來的，由于高斯混合模型能夠平滑地近似模仿任意形狀的密度分布情況［3］，因此近年來經(jīng)常被用于語音、圖像識別等方面，并且取得了良好的效果。可以用提取到的音樂特征，通過訓(xùn)練特征獲取模型參數(shù)的方法獲得不同情緒類別的特征模板，然后進(jìn)行音樂樣本的分類判斷。

在高斯混合模型中，待聚類的數(shù)據(jù)可以看成是來自于多個正態(tài)分布的混合概率分布聚合而成，而這些正態(tài)分布代表著不同的類，所以通常可以采用各個正態(tài)分布的相關(guān)參數(shù)（均值、權(quán)值與協(xié)方差）作為類的參數(shù)。

混合高斯模型的概率密度函數(shù)可以用式（1）表示：

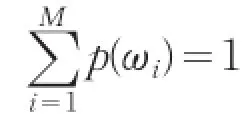
N（X；μi；∑i）為每個子分布的P維聯(lián)合高斯概率分布，如式（3）表示：

由于音樂的特征參數(shù)通常具有平滑的概率密度分布，所以有限數(shù)目的高斯密度函數(shù)足以對音樂的特征參數(shù)形成一種平滑逼近。適當(dāng)?shù)剡x擇高斯混合模型的均值、協(xié)方差和概率權(quán)重，可以完成對一個概率密度分布模型的建模。為了簡化計算，通常可以使協(xié)方差矩陣∑i為對角陣，以減少需要估計的未知變量的數(shù)目，而且不影響最后結(jié)果。本文的音樂情緒建模過程依托于高斯混合模型，用各個高斯分布的參數(shù)來表示音樂特征的統(tǒng)計特性［4］。

1.2Expectation-Maximization算法

高斯混合模型的模型參數(shù)λ通常可以使用一組訓(xùn)練數(shù)據(jù)，按照某種準(zhǔn)則來求出，使得到的高斯混合模型的模型參數(shù)能夠最好地描述給出的訓(xùn)練數(shù)據(jù)的概率分布。這就是最大似然估計（Maximum Likelihood）的思想。首先可以假設(shè) X=為給定的用于訓(xùn)練的特征矢量序列，而GMM的似然度可表示為，訓(xùn)練的目的是為了尋找能使P（X|λ）最大的一組λ。由于高斯混合模型的計算量較大且參數(shù)λ通常為非線性函數(shù)，因此本文采用的求解方法是Expectation-Maximization算法。

Expectation-Maximization（EM）算法是一種從不完全數(shù)據(jù)或有數(shù)據(jù)丟失的數(shù)據(jù)集中求解出模型分布參數(shù)的一種最大似然估計方法。通常在下列兩種情況下，應(yīng)該考慮用EM算法去估計參數(shù)：一是由于觀測過程本身的限制或錯誤，造成了觀測數(shù)據(jù)的丟失；二是參數(shù)的最大似然函數(shù)直接求解十分困難，通過假設(shè)隱含數(shù)據(jù)的存在并且引入隱含數(shù)據(jù)，使得函數(shù)的優(yōu)化可以變得容易。在模式識別領(lǐng)域的問題中，后一種情況更為常見。這時就需要引入隱含數(shù)據(jù)和原來的不完全數(shù)據(jù)組成新的完全數(shù)據(jù)。高斯混合模型的參數(shù)估計求解就屬于第二種情況。

EM算法是一種遞歸最大似然算法，是從一組訓(xùn)練樣本序列中來估計模型的參數(shù)。求解過程通常分為兩步：第一步是要假設(shè)知道各個高斯模型的參數(shù)（可以初始化一個，或者用Kmeans方法設(shè)置），去估計每個高斯模型的權(quán)值；第二步是基于現(xiàn)有估計出來的權(quán)值，再去確定高斯模型的參數(shù)。重復(fù)這兩個步驟，直到波動很小，也就是近似地達(dá)到極值，以此來估計模型參數(shù)。

EM算法迭代的過程（第n+1步）如下：

混合權(quán)值重估迭代公式

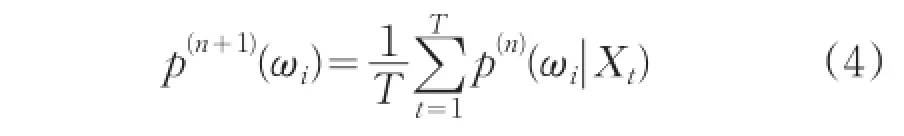
均值重估公式

方差重估公式

三個公式中的后驗概率p（n）（λi|Xt），表示為：

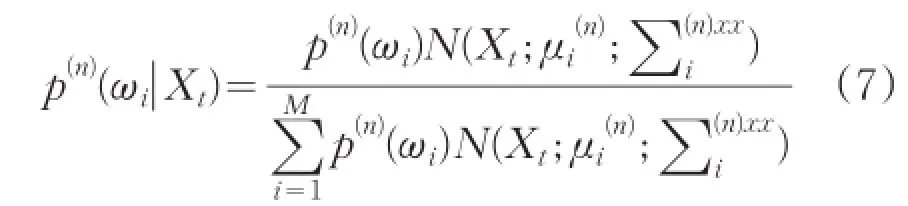
以上公式執(zhí)行了求期望（E步）和最大化（M步）。對EM算法中的E步、M步不斷重復(fù)迭代，當(dāng)找到似然函數(shù)的極大值時停止迭代，此極大值通常即為所求結(jié)果。

2　音樂信號的特征提取

為了能真實有效的反應(yīng)出音樂信號跟情緒有關(guān)的特征，本文提取了共37維特征用于實驗。

2.1梅爾倒譜系數(shù)（MFCC）

人耳聽覺是一個復(fù)雜的非線性的系統(tǒng)，針對不同的頻率人耳展現(xiàn)出不同的靈敏度。其中對音頻中低頻的響應(yīng)是線性的，對高頻部分的響應(yīng)則近似于對數(shù)響應(yīng)［5］。除此之外，MFCC也具有對卷積信道失真進(jìn)行補(bǔ)償?shù)哪芰Γ?］。

Mel頻率與實際頻率的數(shù)值計算關(guān)系可以表示為：

MFCC的求解步驟通常如下：

（1）計算之前要確定好每幀的幀長和幀移，對每幀數(shù)據(jù)進(jìn)行預(yù)加重，然后進(jìn)行離散傅里葉變換，計算模的平方得出離散功率譜S（n）。

（2）使用臨界帶通濾波方法，采用個數(shù)為M個的三角濾波器組Hm（n），利用之前的公式，將實際頻率轉(zhuǎn)化到梅爾頻率上。再計算S（n）經(jīng)過了這一濾波步驟之后的功率值，得出N個參數(shù)pm。

（3）計算pm的自然對數(shù)，得到mj。

（4）對mj計算離散余弦變化，得到梅爾倒譜系數(shù)。

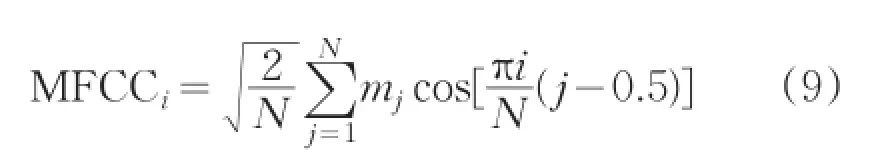
式中，MFCCi表示第K個MFCC，N代表帶通濾波器的個數(shù)，mj是帶通濾波器輸出幅值取平方的對數(shù)。通常的MFCC只表現(xiàn)了語音的靜態(tài)特征，如果想要描述語音的動態(tài)特征則可以計算MFCC的一階差分。研究結(jié)果表明，MFCC能夠較好的作為音頻分類的特征并且能夠提高音頻分類的精確度［7］。MFCC的參數(shù)K通常取到12～16，根據(jù)實際需要靈活改變。根據(jù)之前學(xué)者研究的經(jīng)驗，本文MFCC的K取值為13。

2.2短時時域特征

2.2.1短時能量

音樂信號的能量隨時間的變化明顯，一般清音的能量要比濁音的能量小很多。音樂的短時能量分析，為這些幅度的變化規(guī)律提供了一個和適當(dāng)?shù)拿枋龇椒ǎ?］。離散后的音樂信號x（n）的短時能量定義為：

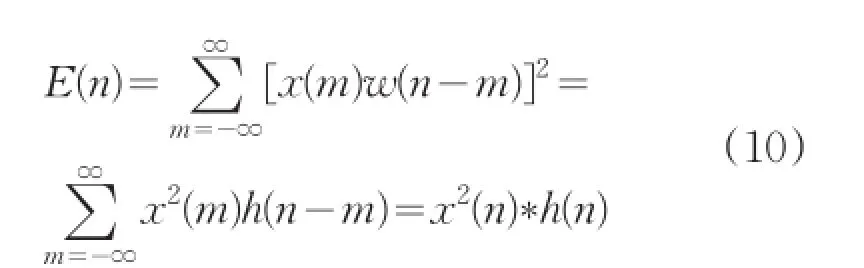
式中h（n）=w2（n）。所以，短時信號可以看成是一個信號的平方通過一個濾波器的輸出。

2.2.2短時平均過零率

短時平均過零率是音樂時域分析中最常用的一種特征參數(shù)，它是指平均每幀信號內(nèi)通過零值的次數(shù)，其實質(zhì)是音樂信號采樣點符號變化的次數(shù)。其公式為：

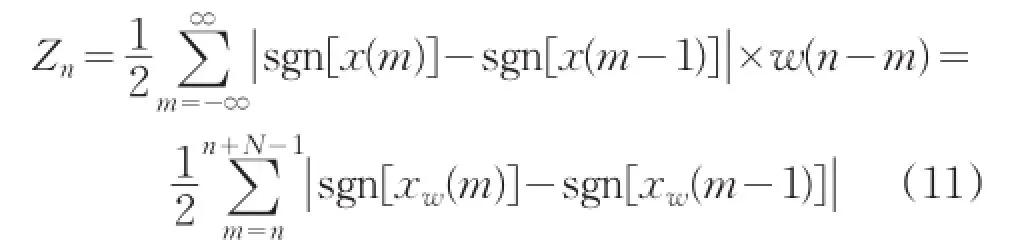
式中sgn［*］是符號函數(shù)。

2.2.3短時自相關(guān)

短時自相關(guān)是音樂采樣信號的第n個樣本點附近用短時窗截取一段信號，其公式定義為：

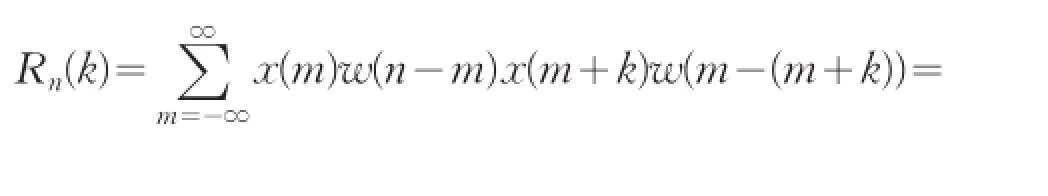
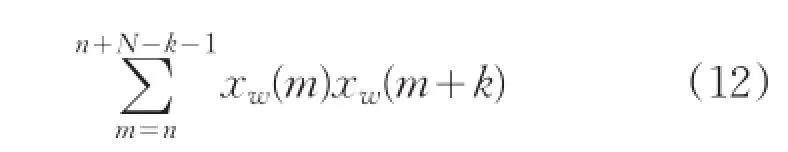
式中，n代表窗函數(shù)從n點開始加入。

2.3子帶特征

按照倍頻程規(guī)則把每一幀短時頻譜分成7個子帶，所以每個子帶就包含了若干頻譜的分量。把每個子帶上最大的頻譜分量、最小的頻譜分量和平均值組合成特征序列。每一幀有7個子帶，每個子帶有三個特征值，所以每一幀具有21維特征值。它能有效地表達(dá)頻譜能量在每一個子帶上的分布情況。

3　實驗過程及結(jié)果

3.1實驗過程

本文主要采用了兩種實驗方法進(jìn)行比較。第一種是直接對四種情緒類型進(jìn)行建模，即分別對激動、愉快、平靜、悲傷四種情緒建立模型GMME、GMMH、GMMP、GMMS。再分別求出每一個測試樣本在這四個GMM下的后驗概率并進(jìn)行比較，后驗概率最大的即認(rèn)為被判決為該種情緒的音樂。

第二種是分別對表示情緒強(qiáng)烈程度的軸arousal的正負(fù)兩端建立模型GMMA+和GMMA-，即用情緒強(qiáng)烈程度高的表示激動和平靜的訓(xùn)練樣本訓(xùn)練GMMA+，用情緒強(qiáng)烈程度低的表示愉快和悲傷的訓(xùn)練樣本訓(xùn)練GMMA-，使這兩個模型表示情緒強(qiáng)烈的正負(fù)。以一個測試樣本來說明，就是求出這個測試樣本在這兩個模型上的后驗概率然后根據(jù)后驗概率判斷其更接近于哪一端。同理，建立為表示情緒正負(fù)的軸valence的兩端建立模型GMMV+和GMMV-。在這種方法下，實際上默認(rèn)組成了一個兩層分類器，即一個測試樣本要先經(jīng)過一個分類器判斷情緒的強(qiáng)烈，再經(jīng)過一個分類器判斷情緒的正負(fù)。通常在涉及到多層分類器的問題上都會有權(quán)值的分配問題。對于權(quán)值的分配本文進(jìn)行了7次試驗來觀察不同權(quán)值下的分類效果，并進(jìn)行比較。

在實驗之前需要對音樂進(jìn)行預(yù)處理。為了計算方便，本文對每首音樂只提取了最能代表其特征的30s的音樂片段。提取片段后需要進(jìn)行預(yù)加重、歸一化及加窗分幀處理。本文預(yù)加重的系數(shù)為-0.9375，所加窗為漢明窗。在默認(rèn)采樣頻率為44100的條件下，分幀的幀長選為1024，幀移為512。每種情緒的訓(xùn)練音樂有10首，共計40首。每種情緒類別的測試音樂有5首，共計20首。

3.2直接建立情緒GMM的實驗結(jié)果

由于GMM階數(shù)的選定尚無統(tǒng)一標(biāo)準(zhǔn)，為了后續(xù)實驗的進(jìn)行，需要對階數(shù)M進(jìn)行比較選取，通常階數(shù)M的選擇為16、32、64，所以本文在前人研究的基礎(chǔ)上對三種階數(shù)下的GMM分類效果分別進(jìn)行實驗，結(jié)果見表1。

表1　不同階數(shù)對GMM正確率的影響

由表1可知，M等于32和64時正確個數(shù)相同，但是由于M等于64時增加了計算量，而且結(jié)果并沒有明顯的優(yōu)勢，所以接下來的實驗中的M選為32。而且M等于64時可能會出現(xiàn)過擬合現(xiàn)象不利于構(gòu)造靈活可用的模型。M等于16時正確個數(shù)偏低是因為出現(xiàn)了欠擬合的情況，即16階的高斯混合模型不足以表達(dá)實際的訓(xùn)練樣本的特征。

3.3建立軸GMM加權(quán)后分類的實驗結(jié)果

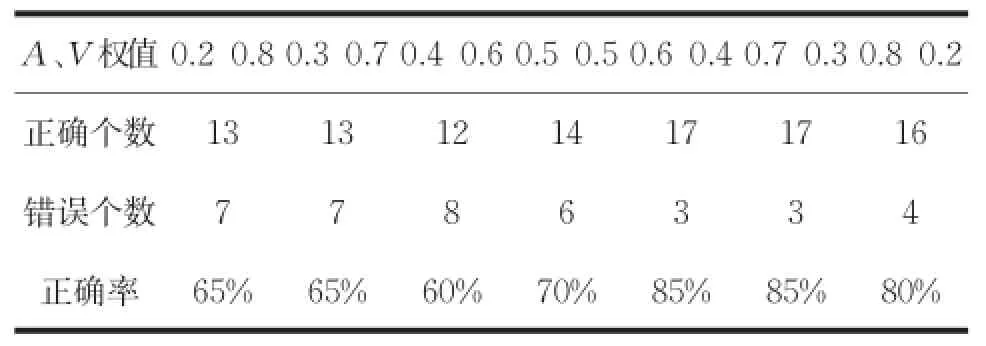
表2　不同權(quán)值對正確率的影響

從表2結(jié)果來看，當(dāng)A、V權(quán)值分配0.6 0.4和0.7 0.3時的正確率一致，所以為了更進(jìn)一步的區(qū)分，再加入十首測試樣本，即使用30首測試樣本進(jìn)行測試。結(jié)果如表3所示。

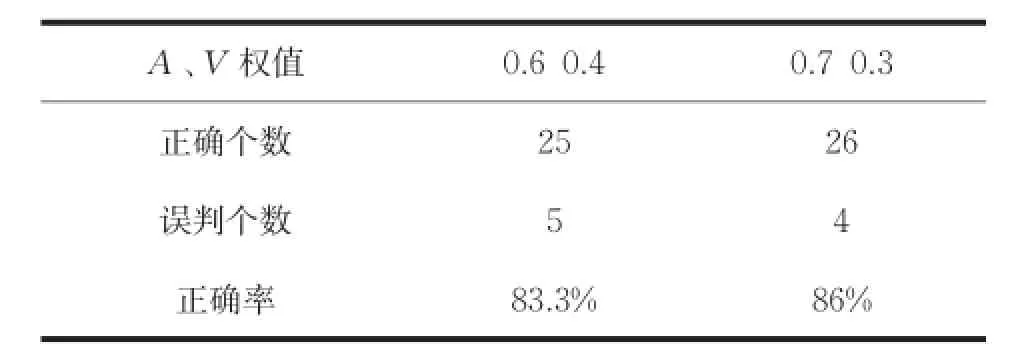
表3　增加測試樣本后兩權(quán)值的比較

結(jié)果表明，在30首測試樣本的測試下，權(quán)值分配為0.7和0.3取得的效果較好。之所以在20首測試樣本下有結(jié)果一樣的情況產(chǎn)生原因主要有兩條：一是所選擇的訓(xùn)練樣本和測試樣本數(shù)過少，沒有更明晰的分辨出優(yōu)劣性；二是所選擇的訓(xùn)練歌曲范圍不夠廣或者類型判別不夠準(zhǔn)確，導(dǎo)致在判別時會出現(xiàn)模糊的狀況。

4　結(jié)論

本文結(jié)合高斯混合模型對四分類音樂情緒進(jìn)行了研究，結(jié)果表明在加權(quán)0.7、0.3的情況下取得的效果最好。與王磊［9］做過的基于Adaboost算法的分類結(jié)果相比較來看，并沒有達(dá)到97%的準(zhǔn)確率，可能是因為本文特征選取的不夠全面，但大體結(jié)果一致。本文在情緒分類上僅僅區(qū)分了易于辨認(rèn)的四類情緒，但是音樂表達(dá)的情緒遠(yuǎn)遠(yuǎn)不止于此，所以在類別的數(shù)量上還有需要增加的空間。

［1］ 徐凱春.音樂情感參數(shù)化系統(tǒng)的研究與實現(xiàn)［D］.廣州：華南理工大學(xué)，2013.

［2］ 龔勛.高斯混合模型（GMM）參數(shù)優(yōu)化及實現(xiàn)［J］.西南交通大學(xué)信息學(xué)院學(xué)報，2010（1）：2-3.

［3］ 程遠(yuǎn)國，耿伯英.基于高斯混合模型的無線局域網(wǎng)定位算法［J］.計算機(jī)工程，2009，35（4）：25-27.

［4］ 時丹.音樂風(fēng)格相似性檢測算法研究［D］.大連：大連理工大學(xué)，2013.

［5］Mesaros A，Astola J.The Mel-Frequency Cepstral Coefficients in the Context of Singer Identification ［C］//ISMIR，2005：610-613.

［6］ 蔣偉.基于高斯混合模型的說話人識別研究［D］.成都：電子科技大學(xué)，2008.

［7］ 李劍.神經(jīng)網(wǎng)絡(luò)在音樂分類中的應(yīng)用研究［J］.計算機(jī)仿真，2010（11）：168-171.

［8］ 徐桂彬.基于相關(guān)主題模型的音樂分類方法研究［D］.蘇州：蘇州大學(xué)，2012.

［9］ 王磊，杜利民，王勁林.基Adaboost的音樂情緒分類［J］.電子與信息學(xué)報，2007，29（9）：2067-2072.

Music Emotion Four Classification Research Based on Gaussian Mixture Model

LU Yang，GUO Bin，BAI Xuemei
（School of Electronic and Information Technology，Changchun University of Science and Technology，Changchun 130022）

For the problem of music emotional complexity and difficult to categorize，we proposed a method to establish Gaussian mixture models in four classifications.On the basis of establish models，we innovated established GMM for shaft at both ends of the emotional model and converted it into two-layer weighted classifier discrimination.The results shows that the GMM for shaft models and weight distribution under the condition of 0.7 and 0.3，the musical work can obtain the best classification result，and the result is better than the result of directly establish models for each type of emotion.

Gaussian mixture model；music emotion classification；weighted judgment

TP343

A

1672-9870（2015）05-0107-05

2015-07-01

陸陽（1991-），男，碩士研究生，E-mail：457625762@qq.com

郭濱（1965-），男，教授，E-mail：guobin@cust.edu.cn