基于差值映射的壓縮感知MUSIC算法
呂志豐 雷 宏
?
基于差值映射的壓縮感知MUSIC算法
呂志豐*①②雷 宏①
①(中國科學院電子學研究所 北京 100190)②(中國科學院大學 北京 100049)
多快拍(MMV)問題旨在恢復具有相同稀疏結構的多列信號。在傳統陣列信號處理中MMV問題的求解通常采用多重信號分類(MUSIC)等確定性方法實現,但當快拍數不足或存在相干源時該類方法失效;而在壓縮感知(CS)的概率求解模型下,即使信源相干也能得到恢復結果,但現有算法普遍性能不足。近期Kim等人的研究表明,將CS與MUSIC相結合可得到比二者更加優秀的性能和更為寬泛的使用條件,該方法被稱作壓縮感知 MUSIC或CS-MUSIC算法。作為一種投影型非凸優化算法,差值映射(DM)最早用于解決X射線晶體學中的相位恢復問題,并逐漸在其他非凸及壓縮感知問題的求解中展示出優良性能。該文提出一種基于差值映射的CS-MUSIC算法,仿真結果表明該算法在MMV問題求解中十分有效,相比經典CS-MUSIC具有更高的恢復成功率。
壓縮感知;多快拍問題;聯合稀疏;多重信號分類;差值映射
1 引言
壓縮感知(Compressed Sensing, CS)[1,2]主要研究在嚴重欠采樣的情況下如何精確恢復具有稀疏結構的信號。其求解理論基于概率模型,通常借助一系列的優化算法來實現信號恢復。近年來CS已成為信號處理領域的研究熱點之一,并且在不同應用方向取得了成功。在CS理論中,多快拍問題(Multiple Measurement Vector, MMV)旨在辨識具有相同稀疏支集的多列未知信號,基于CS的求解算法在快拍數不足和信源相干時仍可得到MMV問題的解,但目前算法在性能上普遍受稀疏度影響嚴重。
在傳統陣列信號處理中,MMV問題等價于波達方向(Direction-Of-Arrival, DOA)估計問題[9]。這類問題的求解往往基于信號和噪聲子空間的確定性模型,通過空間譜掃描得到最終結果,其中以多重信號分類(MUSIC)算法[10]最具代表性。該類方法理論性能良好,但在快拍數不足或信源相干時將失效。
結合CS在使用條件上的寬泛性和MUSIC類算法在性能上的優良性,Kim等人在文獻[11]中創新性地提出了CS-MUSIC算法用于MMV問題的求解。該文獻從理論上給出了CS-MUSIC算法的性能分析,并詳細闡述了CS和MUSIC類算法之間的內在聯系。同期文獻[12]也給出了相似的獨立結果,并將其方法稱為子空間增強型多重分類(Subspace- Augmented MUSIC, SA-MUSIC)。
作為一種非凸優化算法,差值映射[13,14](Difference Map, DM)最早用于解決X射線晶體學中的相位恢復問題[15,16],并逐漸在其他非凸及壓縮感知問題的求解中展示出優良性能[14,17,18]。文獻[18]將DM算法引入到CS單快拍(Single Measurement Vector, SMV)問題的求解和稀疏字典編碼中,結論表明其性能要遠遠優于現有的大多CS算法。
本文將差值映射引入到MMV問題的求解中,并提出了一種基于差值映射的CS-MUSIC算法。仿真結果表明本文所述方法在MMV問題的求解中十分有效,且使得經典CS-MUSIC的恢復性能得到了顯著提高。
本文組織結構如下:在第2節中分別介紹MMV問題、CS-MUSIC算法以及差值映射算法;在第3節中給出DM算法在MMV問題和CS-MUSIC中的具體求解過程;第4節通過數值仿真驗證本文所提算法的有效性和性能優勢。
2 多快拍問題及差值映射算法
2.1壓縮感知和多快拍問題
目前CS框架下用于求解MMV問題的方法主要有貪婪類算法(如同時正交匹配追蹤Simultaneous Orthogonal Matching Pursuit, S-OMP[20,21])、混合范數凸松馳類算法[22,23]、貝葉斯類方法(如多重稀疏貝葉斯學習(Multiple Sparse Bayesian Learning, M-SBL)[24])、隨機類算法(如Reduce MMV and Boost, ReMBo[25])以及基于塊稀疏模型的算法[26,27]等。但當前多數求解算法在性能上與此理論上限還存在相當差距[11],隨著信號稀疏度的變大,信號恢復效果將逐漸變差。
2.2 CS-MUSIC算法
在陣列信號處理的DOA估計中,傳統方法主要有Capon最小方差方法[28]、MUSIC算法[10]、基于旋轉不變技術的信號參數估計(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT)[29]等,其中以MUSIC算法的應用最為廣泛。在信源不相干的條件下,文獻[19]給出了MUSIC算法在MMV問題求解中的性能上限為
這表明在快拍數足夠時,MUSIC算法可達到對MMV問題的理想恢復。但在信源相干條件下,即信號矩陣中存在相關行時,MUSIC算法將失效。
結合CS的概率性重建方式和MUSIC算法的確定性重建方式,Kim等人提出了CS-MUSIC算法[11]。該算法的主要思想是將待恢復的個非零行拆分為兩部分,首先通過壓縮感知算法(如同時正交匹配追蹤(S-OMP)、二閾值(2-thresholding)等)求得行支集,再利用已得支集的信息構建新的噪聲子空間,通過類似MUSIC算法的空間譜掃描計算得出剩余支集位置。CS-MUSIC在接近1時(即單快拍模式)趨于CS算法;而在接近時趨于傳統MUSIC算法[11]。該算法很好地結合了CS和MUSIC的優點,在拓寬使用條件的基礎上保持了優良性能。作者在文中同時指出,即使存在相干信源,CS-MUSIC的恢復性能仍可達到MMV問題的理論上限。
2.3差值映射算法
差值映射算法最早由文獻[13]在解決X射線晶體學中的相位恢復問題時提出。在DM算法中,某一問題的解被看作兩個約束條件集合與的交集,集合,分別描述了該問題解所滿足的一類約束條件。空間點向,的投影分別表示為與,定義為相應集合中與距離最短的點,即
通過在兩個條件集合間的不斷投影,迭代點最終收斂于交集處從而得到問題的解。DM算法的一步迭代定義為
本文將DM算法推廣到MMV問題的求解中,并在CS-MUSIC算法中加以應用。仿真結果表明,本文所述基于DM的CS-MUSIC算法性能優秀,相比原始文獻[11]中的實驗結果在恢復成功率上得到了顯著提升。
3 DM算法在MMV問題求解和CS-MUSIC中的具體實現
3.1 DM求解壓縮感知MMV問題
3.2 基于DM的CS-MUSIC算法
根據3.1節的分析及文獻[11]中對CS-MUSIC算法的描述,本文提出基于DM的CS-MUSIC算法步驟為:

4 仿真實驗結果
4.1隨機MMV問題求解

圖1算法收斂性曲線(SNR=)
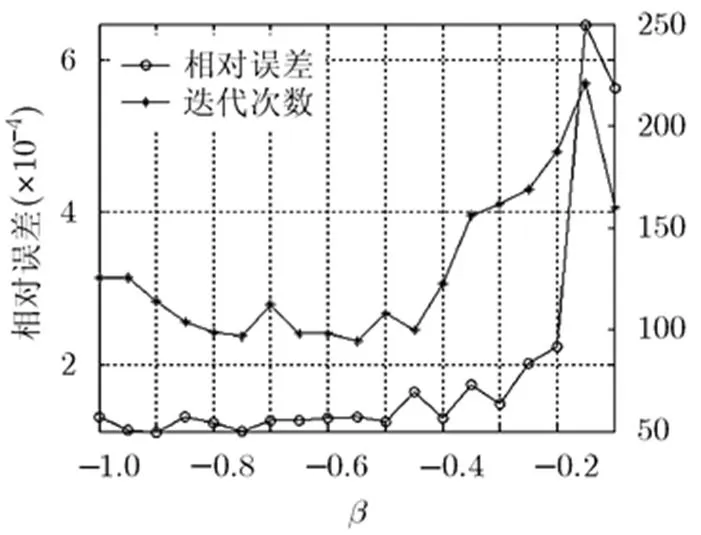
圖2 相對誤差和迭代次數隨參數變化曲線(SNR=)
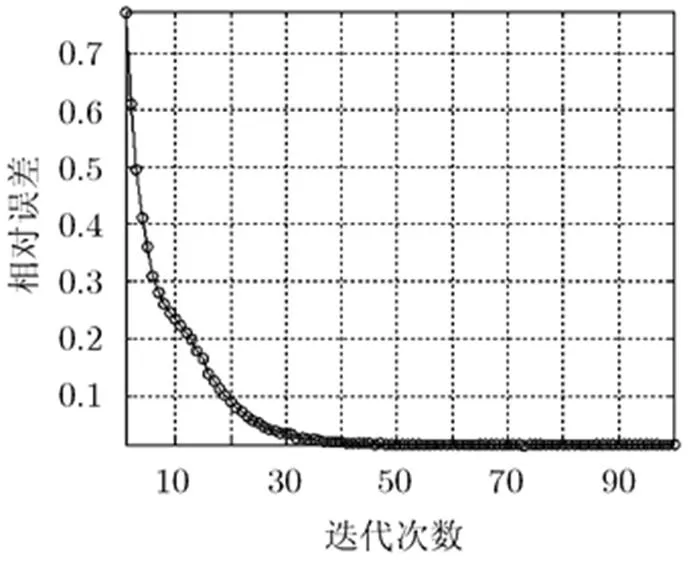
圖3算法收斂性曲線(SNR=40 dB)
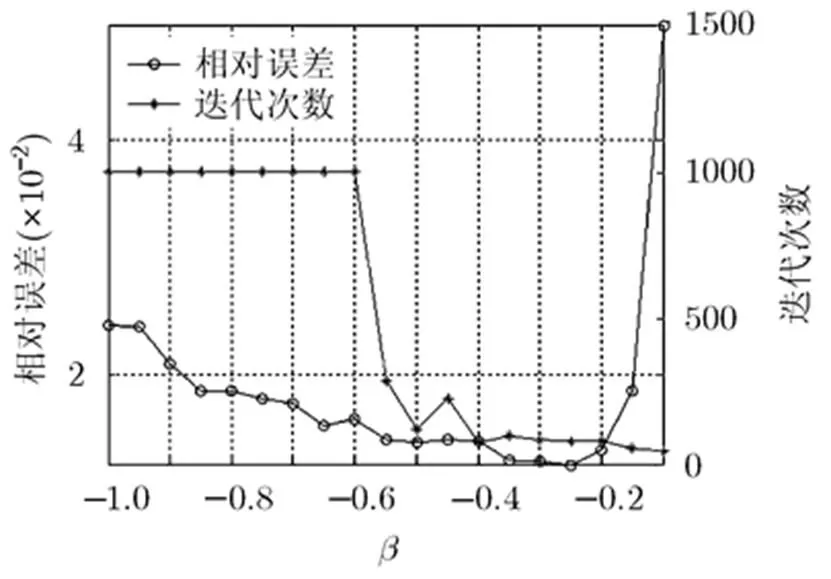
圖4 相對誤差和迭代次數隨參數變化曲線(SNR=40 dB)
4.2 基于DM的CS-MUSIC算法性能比較
這里對本文第3節所述基于DM的CS-MUSIC算法進行仿真實驗,并同文獻[9]中基于S-OMP的算法及傳統MUSIC算法等進行性能上的對比。取高斯分布的隨機信號長度,稀疏度,限制以保證信源相干條件,采樣信噪比;針對內不同陣元數分別進行求解,若所得結果與真實信號支集位置相同則定義為求解成功;重復獨立隨機實驗500次,統計各算法所有值對應的成功概率。實驗中假設信號稀疏度為已知,DM算法參數,,最大迭代次數限制為500。分別對S-OMP算法、傳統MUSIC算法、基于S-OMP的CS-MUSIC算法及本文所述基于DM的CS-MUSIC算法進行上述實驗過程,對快拍數及兩種情形的統計結果分別如圖5、圖6所示。

圖5 恢復成功率隨陣元數變化關系(n=128, r=15)

圖6 恢復成功率隨陣元數變化關系(n=128, r=256)
5 結束語
本文將差值映射算法引入到多快拍問題的求解中,并將其應用于CS-MUSIC算法。數值實驗表明DM算法對MMV問題的求解十分有效,且基于DM的CS-MUSIC算法在性能上具有明顯優勢,可在保持求解精度的條件下有效縮減陣元數量,從而節省陣列信號處理的系統成本。本文算法在求解結果上表現優異,如何從理論上優化參數選擇、加快算法收斂速度,以及分析和提升算法的噪聲魯棒性則是下一步研究的重點。
參考文獻
[1] Donoho D. Compressed sensing[J]., 2006, 52(4): 1289-1306.
[2] Cades E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]., 2006, 52(2): 489-509.
[3] Fang L Y, Li S T, Ryan P,.. Fast acquisition and reconstruction of optical coherence tomography images via sparse representation[J]., 2013, 32(11): 2034-2049.
[4] Yang J, Thompson J, Huang X T,.. Segmented reconstruction for compressed sensing SAR imaging[J]., 2013, 51(7): 4214-4225.
[5] Friedland, S, Li Q, and Schonfeld D. Compressive sensing of sparse tensors[J]., 2014, 23(10): 4438-4447.
[6] Hawes M B and Liu W. Robust sparse antenna array design via compressive sensing[C]. IEEE International Conference on Digital Signal Processing, Nice, France, 2013: 1-5.
[7] Northardt E T, Bilik I, and Abramovich Y I. Spatial compressive sensing for direction-of-arrival estimation with bias mitigation via expected likelihood[J]., 2013, 61(5): 1183-1195.
[8] Nagahara M, Quevedo D E, and Ostergaard J. Sparse packetized predictive control for networked control over erasure channels[J]., 2014, 59(7): 1899-1905.
[9] Krim H and Viberg M. Two decades of array signal processing research: the parametric approach[J]., 1996, 13(4): 67-94.
[10] Schmidt R. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280.
[11] Kim J M, Lee O K, and Ye J C. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing[J]., 2012, 58(1): 278-301.
[12] Lee K and Bresler Y. Subspace-augmented MUSIC for joint sparse recovery with any rank[C]. Proceedings of the IEEE Sensor Array and Multichannel Signal Processing Workshop, Jerusalem, Israel, 2010: 205-208.
[13] Elser V. Phase retrieval by iterated projections[J]., 2003, 20(1): 40-55.
[14] Elser V, Rankenburg I, and Thibault P. Searching with iterated maps[J]., 2007, 104(2): 418-423.
[15] Eldar Y C, Sidorenko P, Mixon D G,.. Sparse phase retrieval from short-time Fourier measurements[J]., 2015, 22(5): 638-642.
[16] Shechtman Y, Beck A, and Eldar Y C. GESPAR: efficient phase retrieval of sparse signals[J]., 2014, 62(4): 928-938.
[17] Qiu K and Dogandzic A. Nonnegative signal reconstruction from compressive samples via a difference map ECME algorithm[C]. Proceedings of the IEEE Statistical Signal Processing Workshop, Nice, France, 2011: 561-564.
[18] Landecker W, Chartrand R, and DeDeo S. Robust compressed sensing and sparse coding with the difference map[C]. IEEE European Conference on Computer Vision, Zurich, Switzerland, 2014:315-329.
[19] Feng P. Universal minimum-rate sampling and spectrum-blind reconstruction for multiband signals[D]. [Ph.D. dissertation], University of Illinois, Urbana-Champaign, 1997.
[20] Chen J and Huo X. Theoretical results on sparse representations of multiple measurement vectors[J]., 2006, 54(12): 4634-4643.
[21] Tropp J A, Gilbert A C, and Strauss M J. Algorithms for simultaneous sparse approximation, Part I: Greedy pursuit[J]., 2006, 86(3): 572-588.
[22] Malioutov D, Cetin M, and Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]., 2005, 53(8): 3010-3022.
[23] Tropp J A. Algorithms for simultaneous sparse approximation. Part II: Convex relaxation[J]., 2006, 86(3): 589-602.
[24] Wipf D P. Bayesian methods for finding sparse representations[D]. [Ph.D. dissertation], University of California, San Diego, 2006.
[25] Mishali M and Eldar Y C. Reduce and boost: recovering arbitrary sets of jointly sparse vectors[J]., 2008, 56(10): 4692-4702.
[26] Eldar Y C, Kuppinger P, and Bolcskei H. Compressed sensing of block-sparse signals: uncertainty relations and efficient recovery[J]., 2010, 58(6): 3042-3054.
[27] Baraniuk R G, Cevher V, Duarte M F,.. Model-based compressive sensing[J]., 2010, 56(4): 1982-2001.
[28] Capon J. High-resolution frequency-wavenumber spectrum analysis[J]., 1969, 57(8): 1408-1418.
[29] Roy R and Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]., 1989, 37(7): 984-995.
[30] Fienup J R. Phase retrieval algorithms: a comparison[J]., 1982, 21(15): 2758-2769.
[31] Bauschke H and Borwein J. On projection algorithms for solving convex feasibility problems[J]., 1996, 38(3): 367-426.
[32] Adiga A and Seelamantula C S. An alternating Lp-L2 projections algorithm (ALPA) for speech modeling using sparsity constraints[C]. IEEE International Conference on Digital Signal Processing, Hong Kong, China, 2014: 291-296.
[33] Yan W, Wang Q, and Shen Y. Shrinkage-based alternating projection algorithm for efficient measurement matrix construction in compressive sensing[J]., 2014, 63(5): 1073-1084.
[34] Hesse R, Luke D R, and Neumann P. Alternating projections and Douglas-Rachford for sparse affine feasibility[J]., 2014, 62(18): 4868-4881.
Compressive Sensing MUSIC Algorithm Based on Difference Map
Lü Zhi-feng①②Lei Hong①-----
①(,,100190,)②(,100049,)
The Multiple Measurement Vectors (MMV) problem addresses the recovery of unknown input vectors which share the same sparse support. The Compressed Sensing (CS) has the capability of estimating the sparse support even in coherent cases, where the traditional array processing approaches like MUltiple SIgnal Classification (MUSIC) often fail. However, CS guarantees the accurate recovery in a probabilistic manner, and often shows inferior performance in cases where the traditional ways succeed. Recently, a novel compressive MUSIC (or CS-MUSIC) algorithm is proposed by Kim., in which both the advantages of CS and traditional MUSIC-like methods are combined together. As an iterative projecting algorithm, Difference Map (DM) is first used to solve the phase retrieval problem in crystallography. Recent results show that it has excellent performance in solving a wide variety of non-convex problems like compressed sensing. In this paper, a DM-based CS-MUSIC algorithm is proposed. Experiments show that the proposed algorithm is very effective in MMV problem solving and the success rate of CS-MUSIC is dramatically improved.
Compressed Sensing (CS); Multiple Measurement Vectors (MMV) problem; Joint sparsity; MUltiple SIgnal Classification (MUSIC); Difference Map(DM)
TN911.72
A
1009-5896(2015)08-1874-05
10.11999/JEIT141542
呂志豐 snowby2010@gmail.com
2014-12-04收到,2015-03-13改回,2015-06-09網絡優先出版
呂志豐: 男,1987年生,博士生,研究方向為壓縮感知、陣列信號處理.
雷 宏: 男,1963年生,研究員,博士生導師,研究方向為電磁場與微波技術、天線理論與工程、信號處理理論與技術.

