一種相機標定方法的探討

王卓君，楊群豐，范　凱，沙鑫美

（1.三江學院，江蘇南京210012；2.中國高速傳動設備集團有限公司，江蘇南京211100）

一種相機標定方法的探討

王卓君1，楊群豐2，范凱1，沙鑫美1

（1.三江學院，江蘇南京210012；2.中國高速傳動設備集團有限公司，江蘇南京211100）

利用多圓陣列平面標定板，以其陣列圓心作為世界坐標參考點，采用基于輪廓跟蹤的區域標記算法提取圖像上多圓區域的形心作為圖像像素坐標系參考點，利用同一標定板不同位置拍攝的多幅圖像，借助每幅圖像的單應性矩陣線性標定出攝像機的內外參數并作為初值，建立非線性優化模型采用最小二乘法進一步優化參數與畸變系數。利用優化的參數對空間點進行投影得到投影平均誤差小于0.05個像素。

攝像機標定；單應性矩陣；線性標定；最小二乘法

0　引言

攝像機標定是計算機視覺獲取三維空間信息的前提和基礎，是雙目視覺研究的重要組成部分。它主要是確定攝像機內外參數的一個過程，即確定攝像機的內部幾何與光學參數（內部參數）和確定攝像機坐標系相對某一世界坐標系的三維位置和方向關系（外部參數）［1］。精確標定攝像機內外參數不僅可以直接提高測量精度，而且為后續的立體圖像匹配與三維重建奠定了良好的基礎；同時，標定的快捷、方便可以更好地滿足農業車輛視覺導航的需要。

相機標定方法有：傳統相機標定法、主動視覺相機標定方法、相機自標定法，可歸結為攝像機標定方法和攝像機自標定方法兩類［2-4］。本研究采用的是前者。

1　攝像機成像模型

為了說明攝像機成像模型，先定義幾種坐標系：世界坐標系、攝像機坐標系、圖像平面坐標系、圖像像素坐標系，理想的攝像機成像模型是針孔模型，各個坐標之間的關系如圖1所示。空間點P從世界坐標系到圖像像素坐標系，需要經過以下4步變換，其中涉及到的參數就是攝像機標定要解決的問題。

（1）從世界坐標系（Xw、Yw、Zw）到攝像機坐標系（Xc、Yc、Zc）的變換，該變換為坐標系的旋轉加上平移構成。

（2）從攝像機坐標系（Xc、Yc、Zc）到圖像平面坐標系（x，y），在不考慮鏡頭畸變的理想情況。

（3）在考慮鏡頭畸變的情況下，無失真坐標（x，y）到受鏡頭畸變而偏移的實際圖像平面坐標（xd，yd）的變換。

（4）實際圖像平面坐標系（xd，yd）到圖像像素坐標系（u，v）的線性變換。

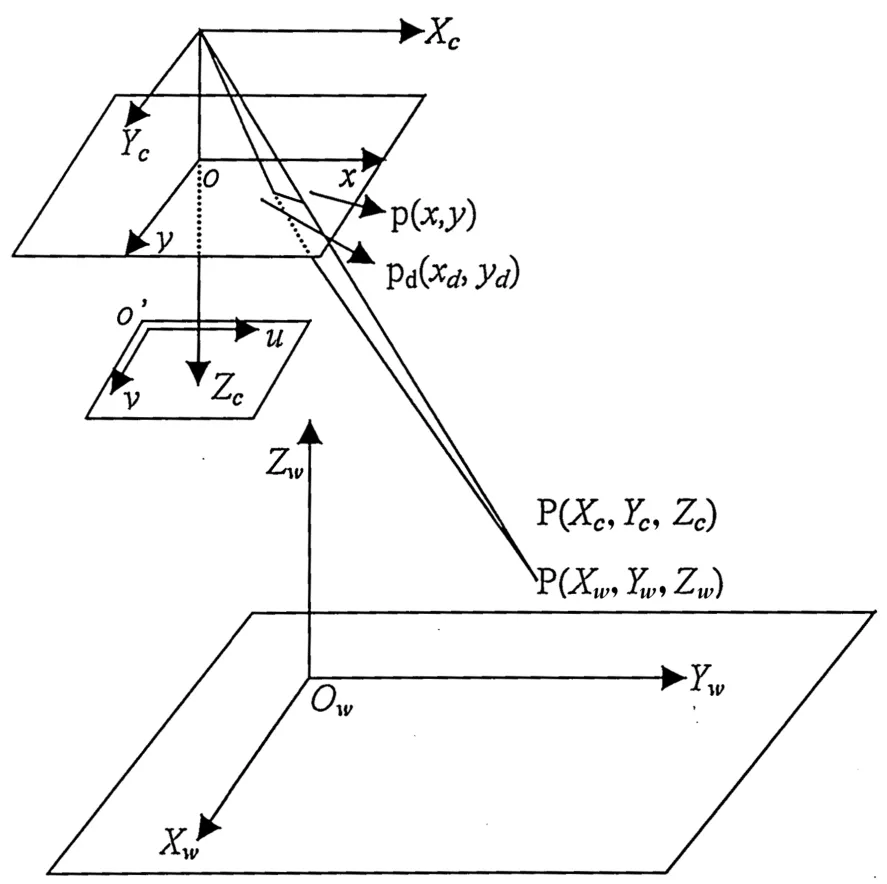
圖1　各個坐標關系圖

圖2　標定面板圖像

2　標定參數求解

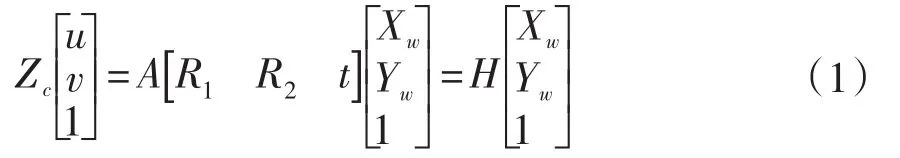
對每一幅圖像（共N幅）中的n個特征點，把Zc看作任意的標量，可以利用線形模型求出3× 3的單應性矩陣H，其中R1，R2為單位正交旋轉矩陣R的第1列與第2列向量，這樣N幅圖像就可以求解出N個單應性矩陣。令］，所以就有對應的N個已知的單應性H矩陣。考慮到R1，R2的正交性，可以得到計算內參矩陣的2個基本約束：，令，由于內參矩陣A是上三角矩陣，可知B是對稱陣，這樣就可以得到關于B矩陣的2N個線性方程［5］，求解此線性方程既可得到B矩陣，繼而可以得到內參矩陣A。進一步利用內參矩陣A可以求出每幅圖像對應的外部參數：。上面求解過程利用了內參矩陣A恒定不變的條件，但是每幅圖像對應的外部參數是變化的，這樣可以得到N個外部參數。

考慮鏡頭畸變，對于徑向畸變系數k1，k2，可以這樣估計其初值：由于通過線性關系求出了相機的內外參數，通過（4）式可以把圖像像素坐標上的特征點（u，v）轉換為圖像平面上的點（xd，yd），同時對空間已知點P（Xw、Yw、Zw）通過（2）式轉換為理想無畸變圖像平面上的點（x，y），再通過（3）式可以建立關于k1，k2的線性方程，共可以建立2n N個方程［5］，求解此方程即可得到k1，k2的初值解。

參數的優化：可以利用上面求得的內外參數以及畸變系數作為初值，通過求解下式的最小值得到優化的參數：

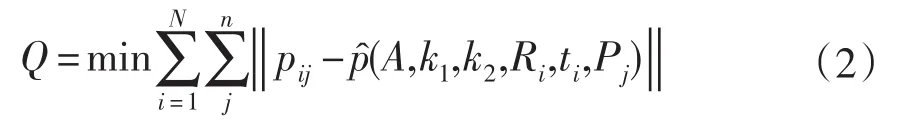
其中pij為第i幅圖像中的第j個特征點的坐標，為利用第i幅圖像中的第j個空間點Pj聯合對應的外部參數Ri，ti計算得到的圖像坐標，這是一個非線性最小化問題，可以采用Levenberg Marquart非線性最小二乘法進行優化求解，它是最快梯度下降法和擬牛頓法的結合方法，速度較快。全厚德［6］等對此問題的算法作了推導。

3　標定結果與分析

標定采用平面式標定板，利用AutoCAD設計7×7個實心圓陣列組成，圓直徑20 mm，圓中心間距為30 mm，用A3打印出來后平整地貼在一面板上，如圖2，并以左下角第一個圓心作為世界坐標系的原點，Xw、Yw軸分別作為圓陣列的行與列方向。相機為BASLER A102fc，焦距10-25 mm可調，在不同位置采集同一標定板N（本例N=10）幅圖像，圖像大小為640×480×24 bits。標定程序利用VC++開發，利用基于輪廓跟蹤的區域標記算法提取圖像上多圓區域，并獲取多圓平面圖像的形心坐標，如圖3，限于篇幅，其算法另文詳述。整個標定過程全自動完成，用戶只需要輸入特征點空間坐標即可。

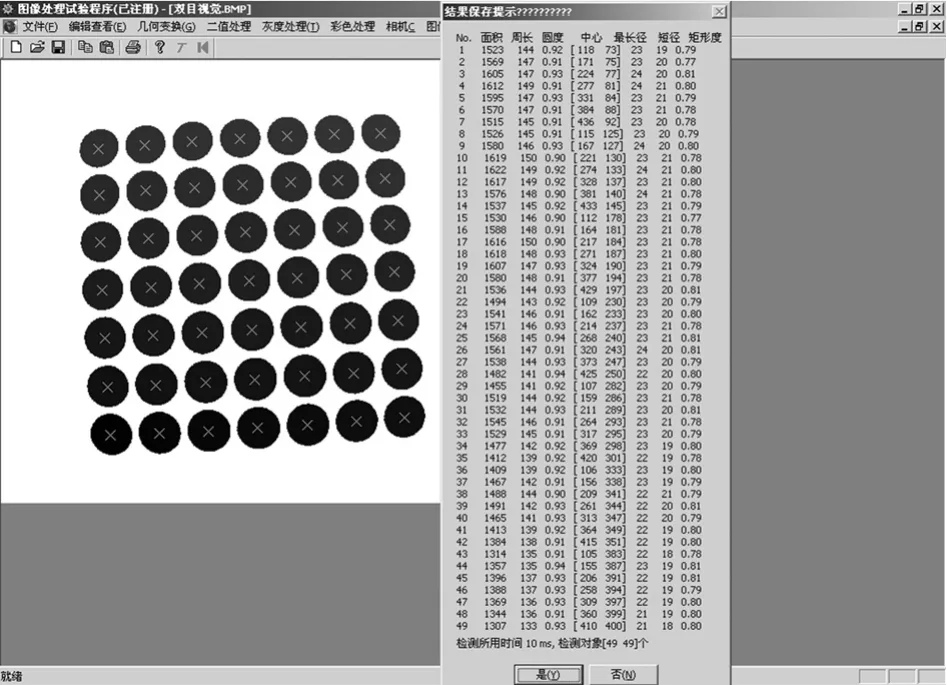
圖3　自動獲取形心坐標檢測效果圖

運用上述算法，攝像機內參標定結果為：

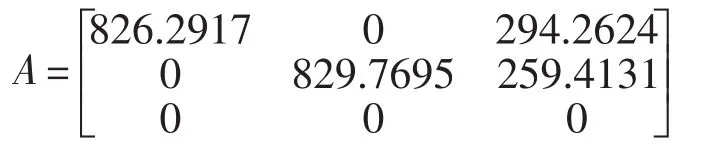
k1=-0.332 0，k2=-0.424 2，同時可以得到10組對應的外部參數矩陣。

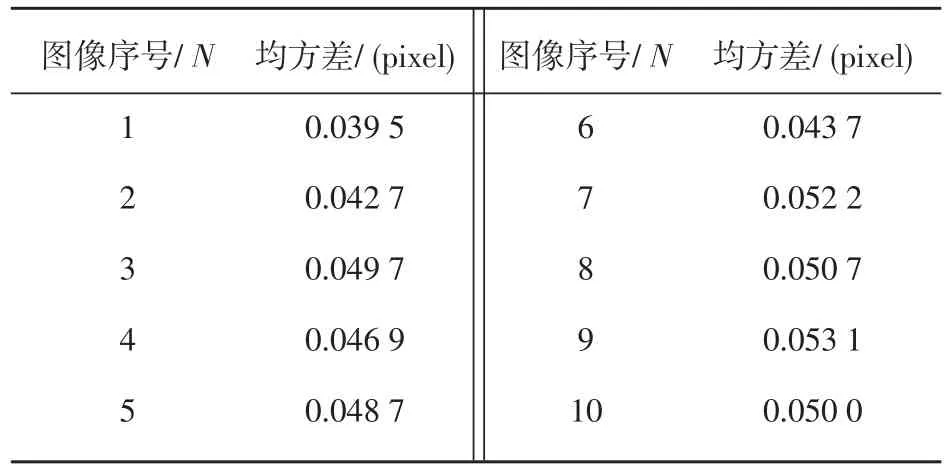
表1　空間點投影均方差

4　結論

通過對攝像機的標定結果可以看出，采用線性的標定方法求取相機內部參數與外部參數，用此參數作為初值，代入非線性優化模型中，通過最小二乘法可以得到準確的內部參數與對應的外部參數，可以滿足平面或者帶有結構特征的空間物體的測量。在實時視覺檢測場合，利用此標定方法，可以先標定相機內部參數，再利用特定的空間坐標點與投影坐標點獲得相應的外部參數，實現攝像機的快速標定。

［1］馬頌德，張正友.計算機視覺［M］.北京：科學出版社，1998.

［2］邱茂林，馬頌德.計算機視覺中攝像機定標綜述［J］.自動化學報，2000，26（1）：43-55.

［3］Emanuele Trucco，Alessandro Verri.Introductor tech?niques for 3-D computer vision［Z］.Prentice Hall，1998.

［4］Tsai R Y.A versatile camera calibration technique for high accuracy 3D machine vision metrology using off--the-shelf TV camera and lenses［J］.IEEE Journal of auto?mation，1987，3（4）：323-334。

［5］蔡健榮，趙杰文.雙目立體視覺系統攝像機標定［J］.江蘇大學學報：自然科學版，2006，27（1）：6-9.

［6］全厚德，閆守成，張洪才.最優化方法在攝像機標定中的應用［J］.火力與指揮控制，2006，31（7）：46-49.

One Method of Camera Calibration

WANG Zhuo-jun1，YANG Qun-feng2，FAN Kai1，SHA Xin-mei1
（1.San Jiang University，Nanjing210012，China；2.China High Speed Transmission Equipment Group Co.，Ltd.，Nanjing211100，China）

In order to get precise camera parameters，one planar template including multi-circles whose centers were regarded as the reference points was designed.Using region labeling arithmetic based on the contour tracking the corresponding shape centers in images were automatically extracted.Every 3D points in the template and their image points produced one Homography matrix，using the multi-images’Homography matrixes the camera intrinsic parameters and external parameters were estimated by solving the closed-form. Finally the estimates were fed to the optimizer as initial guess parameters to get the precise calibration parameters through least square method.The tests indicated that using the final calibration parameters the projection error was not more than 0.05 pixels.

camera calibration；Homography matrix；linear calibration；least square method

TP391

A文獻標識碼：1009-9492（2015）12-0099-03

10.3969/j.issn.1009-9492.2015.12.028

王卓君，女，1976年生，河北保定人，碩士，講師。研究領域：計算機測控技術。已發表論文6篇。

（編輯：向飛）

2015-11-09