運動條件下CHF機理模型開發

劉文興

摘 要：針對運動條件下DNB型臨界熱流密度（CHF），在比對多種機理模型后基于微液層蒸干模型，引入運動條件在流通管道軸向和徑向產生的附加力合附加加速度，開發了適用于運動條件的CHF機理模型，為浮動式核電站熱工安全研究提供理論基礎。

關鍵詞：運動條件 臨界熱流密度（CHF） 微液層蒸干模型 機理研究

中圖分類號：TL33 文獻標識碼：A 文章編號：1674-098X（2015）08（a）-0003-03

浮動式核電站可為極偏遠的近海地區提供穩定電力供應，并在海水淡化領域有良好應用前景。浮動式核電站建在受洋流作用而運動的海面平臺上，海面產生的運動將對核反應堆堆芯臨界熱流密度限值這一熱工安全準則產生影響，使其相對于陸地上靜止條件下臨界熱流密度發生變化，因此從核反應堆熱工安全角度考慮，必須對運動條件下臨界熱流密度特性進行研究。運動條件的影響體現在它會產生一個附加加速度場，管道內的流體將處于重力加速度場和該附加加速度場的疊加場中。對幾種汽泡壅塞模型和微液層蒸干模型進行詳細的研究和對比后，采用Lee和Mudawar[1]的微液層蒸干模型在機理上考慮附加力和附加加速度對于CHF的影響，對運動條件下CHF特性進行研究。

1 機理模型及驗證

1.1 模型構建

微液層蒸干模型假設加熱壁面附近產生的小汽泡結合形成大汽塊，在汽塊下存在非常薄的液相層，稱為微液層。汽塊移動過程中，當汽塊下的液相全部蒸發燒干的時候，該點處的加熱壁面被單相蒸汽覆蓋從而導致傳熱惡化，進而導致DNB發生。因此DNB型CHF可以表達為如下形式：

（1）

式中，δ表示汽塊下微液層厚度/m；UB表示汽塊移動速度/m·s-1；LB表示汽塊長度/m。

這三個參數是求解微液層蒸干模型的關鍵參數，不同的研究者提出不同的δ和UB求解方法和步驟，但都使用汽塊長度等于Helmholtz臨界波長的假設來求解LB[1-8]（圖1）。

模型主要假設包括：①假設每個汽塊的當量直徑等于壁面上汽泡脫離點處的汽泡直徑DB；②當汽塊下微液層完全蒸干時，該點處的加熱壁面被單相蒸汽覆蓋，這時傳熱發生惡化從而達到臨界熱流密度。

該模型中汽塊移動速度UB通過軸向方向施加在汽塊上的浮力和拖拽力二力平衡計算得到（式（5）），微液層厚度δ通過徑向方向施加在汽塊上的力的平衡來確定（式（11））。

不同運動條件將產生的附加加速度場可分解到流道軸向和徑向方向。軸向加速度場影響汽塊軸向浮力FBa，進而對汽塊的移動速度UB產生影響；徑向加速度場使汽塊在垂直于流動方向受到額外浮力FBr，該浮力將打破蒸發力FE和側面提升力FL等力之間原有的平衡并建立新的平衡，汽塊產生徑向移動從而使汽塊下微液層的厚度δ發生變化。汽塊受力示意圖見圖2。

（2）

（3）

（4）

以上各式中，DB表示汽塊當量直徑/m，由Levy[9]模型計算；θ表示管道傾斜角度/°；CD表示拖拽系數/[-]，由Chan和Prince[10]推薦的適用于高壓條件的關系式計算；UBL表示汽塊中心線所處的徑向位置處的主流速度/m·s-1。（UB-UBL）表示汽塊相對主流的移動速度。

聯立式（2）～（4），汽塊速度可以表達成如下形式：

（5）

當地流速UBL用Karman速度分布方程確定。汽塊的長度LB為Helmholtz臨界波長：

（6）

微液層的厚度δ由徑向方向施加在汽塊上的力的平衡來確定（圖2），靜止條件下汽塊主要受兩個力[1]，分別為液相蒸發產生的蒸發力（7）和徑向速度梯度導致汽塊旋轉從而產生的側面提升力（8）[11]。運動條件下，由于氣泡處在徑向附加加速度場中受到徑向浮力FBr（9），蒸發力與徑向浮力將推動汽塊遠離加熱壁面，而側面提升力則由于汽塊旋轉使汽塊靠近壁面，因此徑向力的平衡可以表達為式（10）。

（7）

（8）

（9）

（10）

聯立式（9）～（10），結合相應的本構方程推導得δ表達式：

（11）

求出δ、UB和LB以后，代入式通過迭代計算得到臨界熱流密度值。

1.2 程序開發

基于所開發模型，使用標準FORTRA

N90程序語言，開發了運動條件下CHF分析程序，程序采用模塊化結構，主要包括：輸入模塊、數理模型模塊、物性模塊和輸出模塊等。

對于給定的流通管道幾何尺寸和進口條件，計算時先假設一個初始的熱流密度值qm，然后計算δ，UB和LB等參數，最后通過式計算臨界熱流密度，當計算的qCHF與假設的qm相同時達到收斂；否則改變qm值并重新迭代直到收斂。

1.3 模型驗證

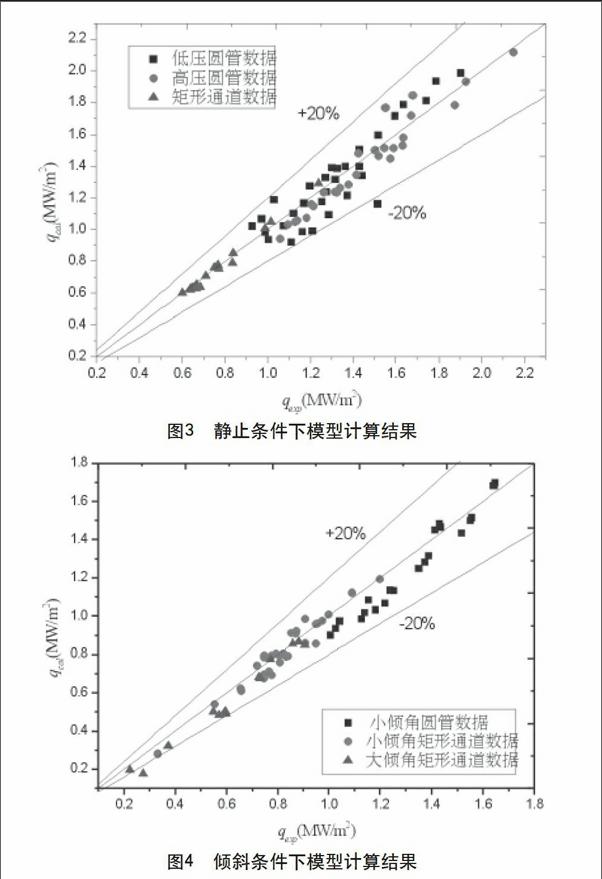
利用所開發模型，對靜止和傾斜條件下獲得的臨界熱流密度實驗數據進行計算，結果如圖3和圖4所示。圖3為豎直靜止條件下不同通道和不同工況的CHF計算值與實驗值對比，實驗數據共80個，預測精度±20%；圖4為傾斜條件下不同通道和不同傾角的CHF計算值與實驗值對比，實驗數據共66個，預測精度±20%。運動條件的主要影響是在流道軸向和徑向產生附加外力，由實驗值與計算值的對比可見，該模型在不同流道、不同工況和不同傾角條件下，對靜止條件下CHF具有較好的預測能力，同時能夠正確的反應運動條件下引入的軸向和徑向附加加速度場產生的影響。

2 結語

針對運動條件下臨界熱流密度，基于微液層蒸干模型開發了DNB型CHF的機理模型并進行了模型驗證，模型具有明確的物理意義，良好的擴展性和較高的預測精度，同時將附加加速度場分解到軸向和徑向使得該模型可以擴展到不同形式運動條件應用。endprint

參考文獻

[1]Lee CH，Mudawar I.A mechanistic critical heat-flux model for subcooled flow boiling based on local bulk flow conditions[J].International Journal of Multiphase Flow，1988，14（6）：711-728.

[2]Katto Y.A prediction model of subcooled water-flow boiling chf for pressure in the range 0.1-20-MPa[J].International Journal of Heat and Mass Transfer， 1992，35（5）：1115-1123.

[3]Celata GP，Cumo M，Mariani A， et al.Rationalization of existing mechanistic models for the prediction of water subcooled flow boiling critical heat-flux[J].International Journal of Heat and Mass Transfer，1994，37：347-360.

[4]Liu W，Nariai H，Inasaka F. Prediction of critical heat flux for subcooled flow boiling[J]. International Journal of Heat and Mass Transfer，2000，43（18）： 3371-3390.

[5]Lin WS，Lee CH，Pei BS.An improved theoretical critical heat flux model for low-quality flow[J].Nuclear Technology，1989，88：294-306.

[6]Katto Y.A physical approach to critical heat flux of subcooled flow boiling in round tubes[J]. International Journal of Heat and Mass Transfer，1990，33（4）：611-620.

[7]Katto Y.Prediction of critical heat flux of subcooled flow boiling in round tubes[J]. International Journal of Heat and Mass Transfer，1990，33（9）：1921-1928.

[8]Celata GP，Cumo M，Katto Y，et al.Prediction of the critical heat flux in water subcooled flow boiling using a new mechanistic approach[J].International Journal of Heat and Mass Transfer， 1999，42（8）：1457-1466.

[9]Levy S.Forced convection subcooled boiling-prediction of vapor volumetric fraction[J]. International Journal of Heat and Mass Transfer，1967，10（7）： 951-965.

[10]Chan BKC，Prince RGH. Distillation studies-viscous drag on a gas bubble rising in a liquid[J].Aiche Journal，1965，11 （1）：176-192.

[11]Beyerlein SW，Cossmann RK， Richter HJ.Prediction of bubble concentration profiles in vertical turbulent 2-phase flow[J].International Journal of Multiphase Flow，1985，11（5）：629-641.endprint