廣義分式規(guī)劃的對偶性

李向有，張慶祥

（延安大學數學與計算機學院 陜西 延安 716000）

0 引言

B-(p,r)不變凸函數[1]是一類重要的不變凸函數，很多學者利用這一函數研究了大量凸規(guī)劃，得到了許多重要結論[2-6].但是這些文章只是利用B-(p,r)不變凸函數研究了常規(guī)的單目標規(guī)劃問題，并且研究內容有很大的重合，Anurag Jayswal[7]研究了極大極小分式規(guī)劃問題，對文獻[8-9]中的相關結論進行了推廣.上述文獻都是利用B-(p,r)不變凸函數，研究相應的規(guī)劃問題，沒有對B-(p,r)不變凸函數進行推廣.極大極小分式規(guī)劃是凸規(guī)劃里的一個重要研究內容，如文獻[8-11]中利用不同的凸函數研究了相應極大極小分式規(guī)劃問題最優(yōu)性和對偶性問題.在上述文章的基礎上，定義了一類新的廣義凸函數：B-(p,r,a)不變凸函數、B-(p,r,a)不變擬凸函數、B-(p,r,a)不變偽凸函數，這些函數是對B-(p,r)不變凸函數的重要推廣，并用這些函數研究了極大極小分式規(guī)劃問題，在更弱的凸性下，對文獻[8-11]中的相關結論進行了更大的推廣，得到了一些重要結果.

1 基本定義

實值函數f:Rn→R是局部Lipschitz的，若對任意x∈Rn，存在一個正數k和x的鄰域N()x，對任意y,z∈N(x)，使得‖f(y)-f(z)‖ ≤k‖y-z‖.

若函數f為局部Lipschitz的，那么函數f:X→R在x沿方向d的Clarke廣義方向導數和Clarke廣義方向梯度分別定義為：

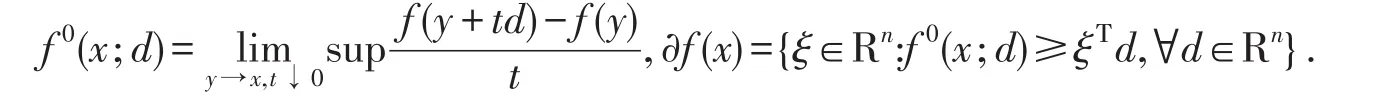
定義1設非空開集X?Rn,f:X→R是X上的Lipschitz函數，p,r是任意非零實數，u∈X,若?x∈X，存在向量函數η:X×X→Rn，函數b:X×X→R+，a:X×X→R，使得對?ξ∈?f(u)有：

成立，則稱f在u點為關于函數η的B-(p,r,a)不變凸函數.

定義2設非空開集X?Rn,f:X→R是X上的Lipschitz函數，p,r是任意非零實數，u∈X,若?x∈X，存在向量函數η:X×X→Rn，函數b:X×X→R+，a:X×X→R，使得對?ξ∈?f(u)有：

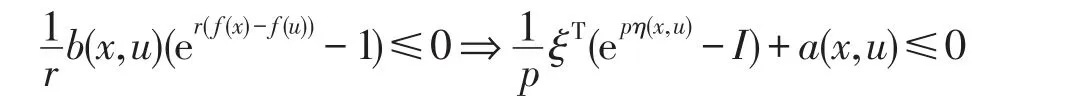
成立，則稱f在u點為關于函數η的B-(p,r,a)不變擬凸函數.

定義3設非空開集X?Rn,f:X→R是X上的Lipschitz函數，p,r是任意非零實數，u∈X,若?x∈X，存在向量函數η:X×X→Rn，函數b:X×X→R+，a:X×X→R，使得對?ξ∈?f(u)有：

成立，則稱f在u點為關于函數η的B-(p,r,a)不變偽凸函數.

2 對偶性

考慮如下的分式規(guī)劃問題：

其中:x∈D?Rn，Y是Rm中的緊子集，f(.,.):Rn×Rm→R是Lipschitz函數且f(x,y) ≥0，h(.,.):Rn×Rm→R是Lipschitz函數，h(x,y) ＞0，g(.):Rn→Rp是 Lipschitz函數.J={1,2,…,q}，

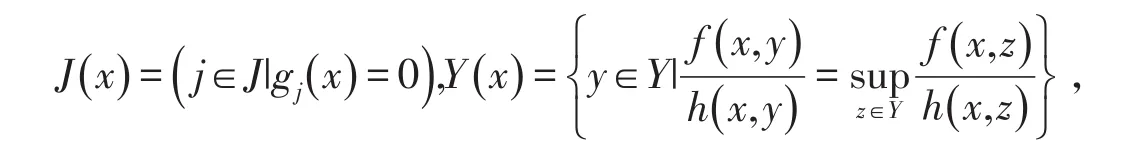
K=現提出如下Mond-Weir對偶問題

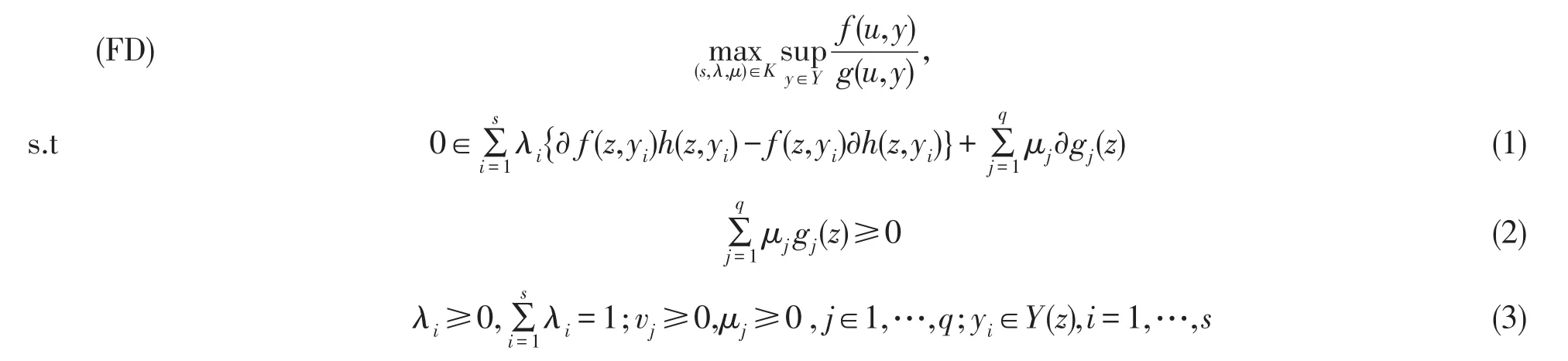
這里H(s,λ,μ,y)表示滿足條件(1)～(3)的 (z,λ,μ,y)的集合，如果H(s,λ,μ,y)是空集，則規(guī)定它的上確界為-∞.

定理1（弱對偶定理）假設

1)x,(z,s,λ,μ,yˉ)分別是（P），(FD)的可行解；

3)b0(x,z)＞0,b1(x,z)＞0 且a(x,z)+c(x,z)≥0,則

定理 1 的證明因為x,(z,s,λ,μ,yˉ)分別是（P），(FD)的可行解，所以有又b1(

x,z)＞0故有

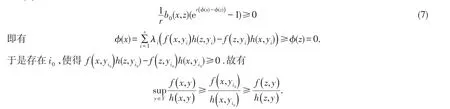
定理2（強對偶定理）假設

1)x0是（P）的最優(yōu)解，?gj(x0),j∈J(x0)線性無關，(z,s,λ,μ,yˉ)是(FD)的最優(yōu)解；

2)?(x)=在z處為關于函數η,b0的B-( )p,r,a不變偽凸函數，在z處為關于函數η,b1的B-( )p,r,a不變凸函數；

3)b0(x,z)＞0,b1(x,z)＞0且a(x,z)+c(x,z)≥0.則（P）和(FD)的最優(yōu)值相等.

證明類似于文獻[6]中定理3的證明.

定理3（嚴格逆對偶定理）假設

1)x0是（P）的最優(yōu)解，?gj(x0),j∈J(x0)線性無關，(z,s,λ,μ,yˉ)是(FD)的最優(yōu)解；

2)?(x)=在z處為關于函數η,b0的B-( )p,r,a不變凸函數，在z處為關于函數η,b1的B-(p,r,a)不變擬凸函數；

3)b0(x,z)＞0,b1(x,z)＞0且a(x,z)+c(x,z)＞0.

則x0=z，即z也是（P）的最優(yōu)解.

定理3的證明假設由于x0≠z,則由定理2可得（P）和(FD)的最優(yōu)值相等.

又在z處為關于函數η，b1的B-( )p,r,a不變擬凸函數，故?τj∈?gj(z),使得

由（5-6）式和a(x,z)+c(x,z)≥0，可得

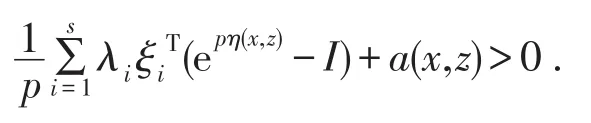
又?(x)=在z處為關于函數η，b0的B-( )p,r,a不變凸函數，故

即有

于是存在i0，使得故有

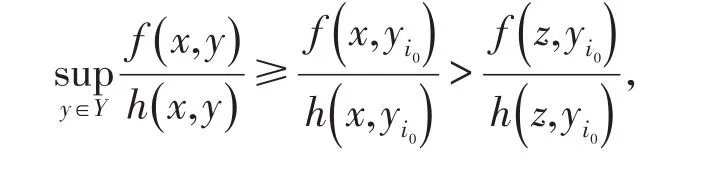
而這與定理2結論矛盾.

[1]Antczak T.A class of B -(p,r) invex functions and mathematical programming[J].J Math Anal Appl，2003，286:187-206.

[2]Liang Zhian，Zhang Zhenhua.The efficiency conditions and duality for uniform invex multiobjective program[J].OR Transactions，2009，13(1): 44-50.

[3]Zhang Ying，Zhu bo，Xu yingtao.A class of Lipschitz B -(p,r) -invex functions and nonsmooth programming[J].OR Transactions，2009，13(1): 61-71.

[4]Antczak T.Generalized B -(p,r) -invexity functions and nonlinear mathematical programming[J].Numerical functional Analysisand Optimazation，2009，30:1-22.

[5]孫玉華，張艷.B-(p,r)不變凸規(guī)劃問題的最優(yōu)性討論[J].遼寧師范大學學報，2005，28(2):139-142.

[6]李向有，張慶祥.廣義Ⅰ型函數的對偶性條件[J].貴州大學學報，2014，31(2):22-24.

[7]Anurag Jayswal.Non-differentiable minimax fractional programming with generalized α - univexity[J].Journal of computationaland applized mathematic，2008，214:121-135.

[8]Liu J C ，Wu C S . On minimax fractional optimality conditions with Invex[J]. J Math Anal Appl，1998，219:21-35.

[9]Liu JC ，Wu CS ，Shen R L.Duality for fractional minimax programming[J].Optimization，1997，41:117-133.

[10]Kim D S，Kim SJ.Optimality and duality for a class of nondifferentiable multiobjective fractional programming problem[J].J Math Anal Appl，2006，305:227-229.

[11]Soghra Nobakhtian.Optimality and duality for nonsmooth multiobjective fractional programming with mixed constraints[J].J Glob Optim，2008，41:103-115.