基于自適應平方根UKF的微機械傳感器融合航姿估計①

馬幫立

（鄖陽師范高等專科學校物理與電子工程系，湖北 十堰 442700）

0 引言

航姿估計廣泛應用于導航制導、智能交通、光電穩定平臺以及慣性穩定平臺等系統中[1].但是，目前廣泛使用的車載航姿測量系統大多是基于高精度慣性器件和GPS組合的姿態航向參考系統(attitude and heading reference system，AHRS)，造價昂貴，嚴重制約了車載航姿測量系統的應用和推廣.快速發展的微機電技術(micro-electromechanical systems，MEMS)為開發低成本航姿估計系統提供了很好的方向.目前，采用MIMU(MEMSinertialmeasurementunit，MIMU)和GPS設計組合導航系統已成為導航領域研究的熱點[2].

目前廣泛報道的航姿估計方法[3-5]依靠陀螺積分得到姿態角，增加輔助傳感器校正陀螺漂移，利用微機械慣性器件構成低成本姿態估計，采用MEMS陀螺、MEMS加速度計以及磁傳感器估計姿態.但采用加速度計測量重力分量估計水平姿態，容易受到載體機動加速度的影響.文獻[3]中采用測量手臂姿態，沒有考慮機動加速度干擾問題.文獻[4]中采用開關判斷即g判斷，加速度測量矢量的范數大于g時不融合，文獻[5]中研究了機器人的姿態估計問題，也采用了開關判斷，采用卡爾曼濾波器對陀螺零偏值進行估計，克服載體的機動加速度對加速度計姿態測量的影響.但3個姿態角的估計開關同時控制，不能區分線加速度和向心加速度，估計精度受到影響，特別是對于兩種機動加速度交替連續出現的情況，系統無法工作；同時該開關算法對于車體振動等外界干擾過于敏感，判斷誤差較大；采用的互補濾波器無法給出陀螺零偏估計，短時間無測量值時難以利用陀螺積分保持精度.

本文中采用姿態估計結構即由陀螺積分得到姿態角，輔以磁強計和加速度計校正陀螺漂移[3-5]，并提出一種新的基于自適應平方根UKF算法，估計和補償機動加速度，有效克服了開關判斷即g判斷的缺陷.跑車實驗結果表明，該算法有效地去除機動加速度的干擾，提高車輛的航姿估計精度.

1 系統原理與姿態運動學描述

陀螺的動態響應較好，在短時間內精度較高，但是存在慢變的零偏誤差，積分得到的角度存在隨時間積累的誤差，長期精度較低.通過加速度計測量重力分量可以得到載體的俯仰角和橫滾角，不存在隨時間的累積誤差，長期精度較好，但是加速度計對于車輛振動等噪聲比較敏感，短時精度不高.因此，利用陀螺與加速度計的互補特性可以得到較好的水平姿態估計.但是，當載體存在機動加速度時，如線加速度(起步、剎車等)和向心加速度(轉彎)，會帶來較大的姿態估計誤差，因此利用陀螺和加速度計融合得到姿態角需要去除機動加速度的影響.

四元數在描述剛體旋轉方面有獨特的優勢，不僅是參數最少的無奇異姿態表示方式，而且用四元數表示的時間傳遞方程是線性的，在計算過程中避免了歐拉角奇異問題以及復雜的三角函數非線性關系[6].姿態四元數是基于剛體旋轉繞矢量軸一次轉成的原理，由4個分量表示為

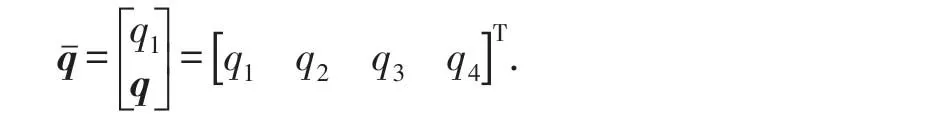
四元數與方向余弦矩陣Cbn(qˉ)有關系

其時間傳遞方程為

其中

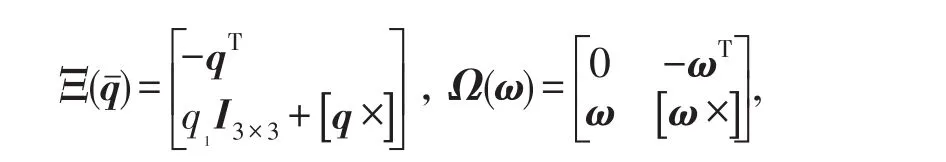
其中ωt為真實角速度，b為陀螺零偏，nω與nb分別為零均值與白噪聲，（3）式中，由于微機械（MEMS）陀螺精度較低，地球自轉角速度以及載體運動牽連角速度可以忽略不計，因此認為微機械陀螺測量數據中只包含有載體姿態變化角速度和陀螺零偏噪聲.

參考慣性導航中的比力方程[6]可得，加速度計量測值為為求角速度矢量的反對稱矩陣.

陀螺誤差的一般建模為慢變零偏以及測量白噪聲，慢變零偏認為是白噪聲驅動的隨機游走[7]

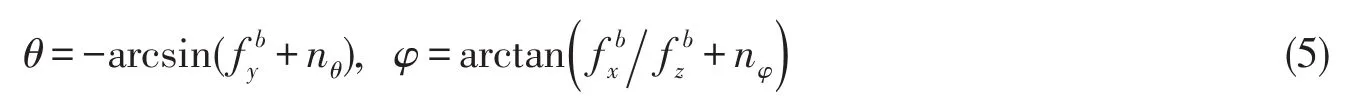
式中的θ為俯仰角，φ為橫滾角為載體坐標系的加速度計測量的重力的3個分量，單位為g，nθ與nφ分別為加速度計的測量誤差.

2 UKF融合估計姿態

姿態估計是典型的非線性問題，可以采用的方法有擴展卡爾曼濾波器算法(extended Kalman filter，EKF)、無味卡爾曼濾波器算法(unscented Kalman filter，UKF)以及粒子濾波器算法(particle filter，PF)等.其中EKF算法復雜度最低，但是存在較大的線性化誤差，對初值的要求較高，較大的初值誤差可能導致其發散，同時求解Jacobian較為復雜；PF算法估計精度高，但是由于采用隨機采樣傳遞狀態的概率密度函數，其計算量很大，對于多維系統，難以做到實時估計；而UKF算法在克服EKF算法缺點的同時計算量適中，利于實時估計[8].為了增強濾波器的穩定性，采用平方根形式的UKF算法，保證協方差陣的正定性，其算法實現過程如下：

1)初始化，

式中，S0為初始方差陣的Cholesky分解.

2)計算采樣點，采用對稱采樣的采樣點為2n+1個，其中γi,i=0,2,…,2n為Sigma點序列[9]，

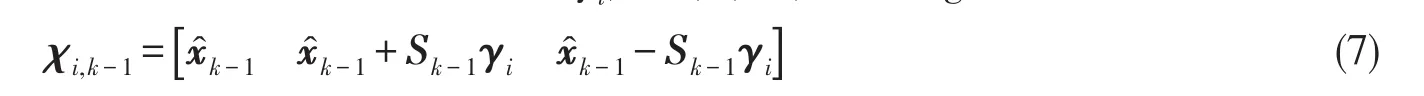
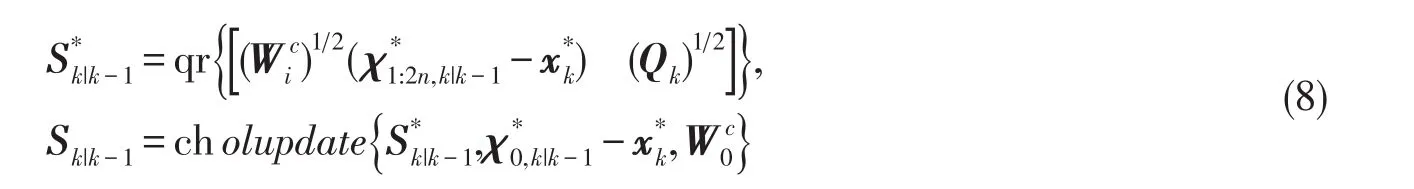
4)更新采樣點，利用一步預測值更新采樣點，

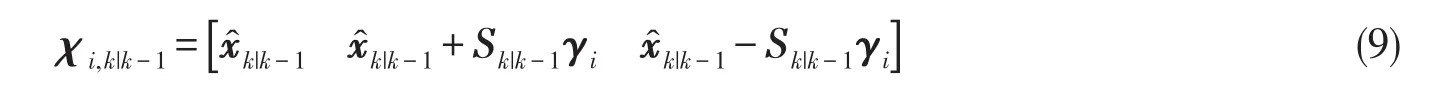
其中，

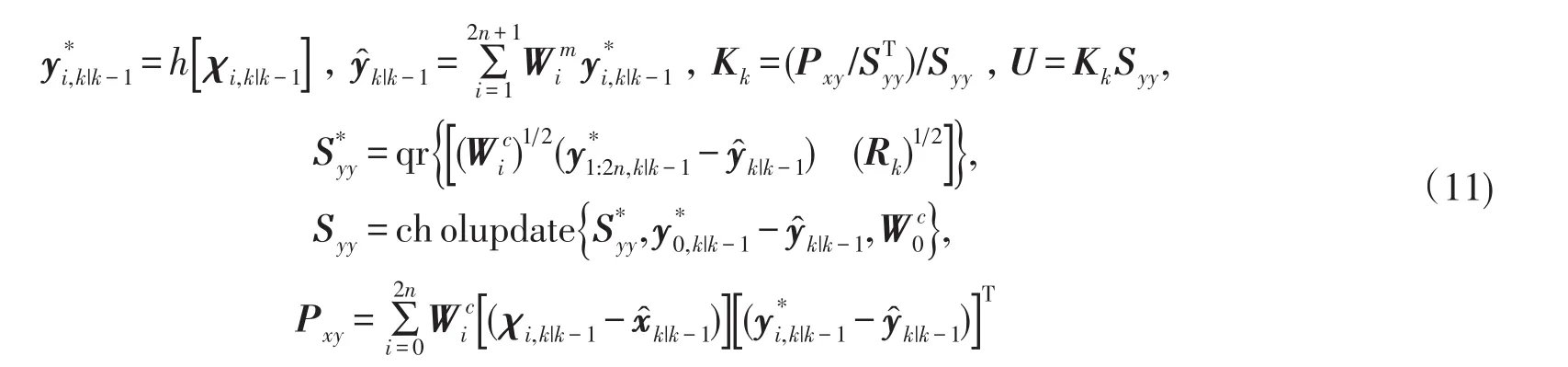
其中chol{·}為Cholesky分解，qr{·}為QR分解，cholupdate{·}為平方根矩陣的更新[9].

由于陀螺零偏誤差較大，因此狀態變量含有需要估計的姿態角及陀螺零偏誤差，即狀態變量為由(2)～(3)式得到狀態方程為

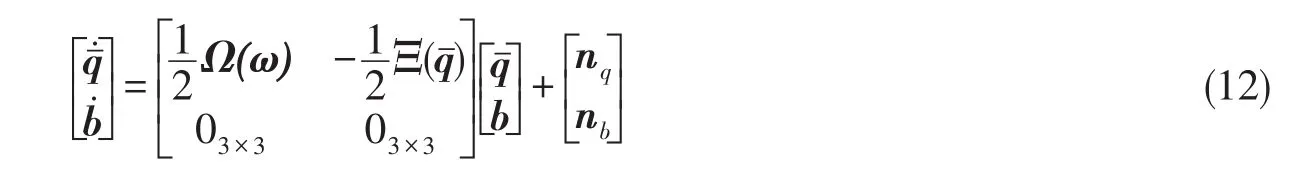
由(5)式，結合歐拉角與四元數的關系[6]，得到不考慮機動加速度時的測量方程為

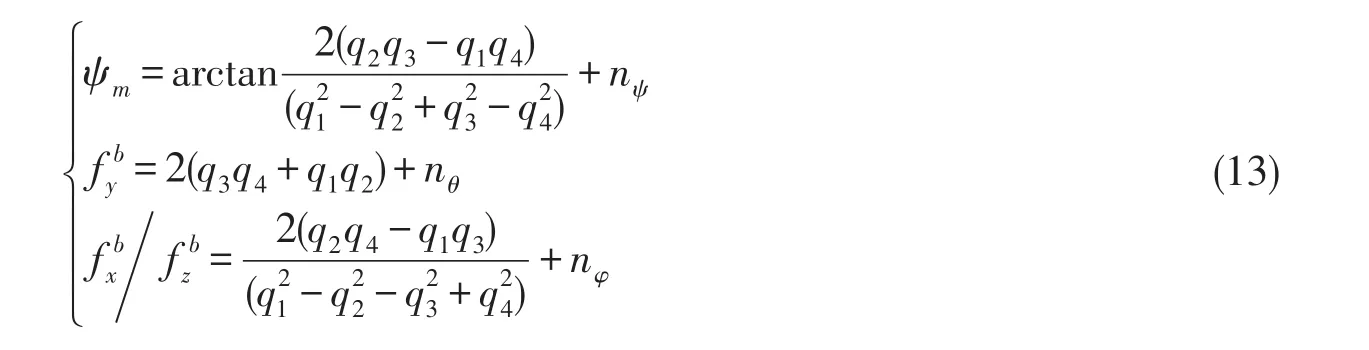
式中的ψm由磁強計得到，通過水平姿態角的一步預測值進行磁強計測量的水平姿態補償，得到水平面內的磁強計測量分量，然后通過反正切計算得出航向角[10]，式中的nψ為測量誤差.將狀態方程(12)～(13)式帶入平方根UKF算法中即可實現航姿融合估計，同時可以實現微機械陀螺（包含航向陀螺，俯仰陀螺以及橫滾陀螺）的零偏估計和校正.

3 自適應UKF算法

(13)式中的俯仰角和橫滾角由加速度計測量得到，未考慮機動加速度對姿態角測量的干擾.由(4)式可知，在有機動加速度干擾的情況下，實際的測量值為

式中的ax、ay分別為車輛機動引起的向心加速度和前向加速度，這些機動加速度值均會體現在濾波過程中的測量更新階段即殘差中.定義測量矢量為機動加速度矢量為ak=[0,ay,k,ax,k]T，則殘差表示為rk=yk-y^k|k-1，由于其中含有機動加速度干擾，故殘差的協方差為

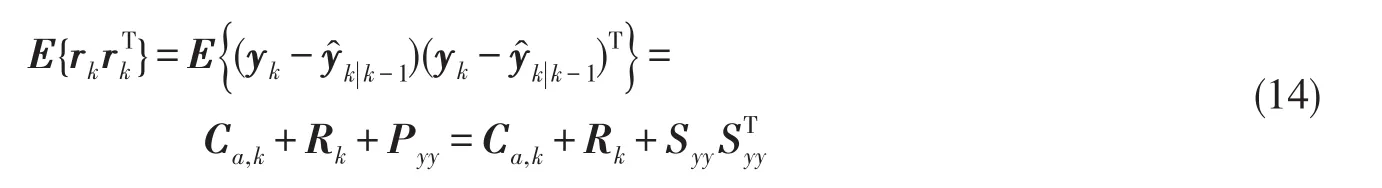
式中的Syy由(11)式得到，Rk為測量噪聲，Ca,k為機動加速度矢量，是ak的協方差矩陣，即

如果能夠估計協方差矩陣Ca,k，則可以分別計算車輛的向心加速度與前向加速度干擾.

新息序列的協方差可以通過如下公式近似得到

式中的N為估計滑動窗，通過（16）式可得到Ca,k的估計值

結合(15)～(17)式可得到機動加速度的估計值.但是，該方法必須保證(17)式給出的協方差矩陣的估計值是正定的，因此，必須對(17)式作必要的改動.由于Wk為對稱矩陣，對其做特征值分解，可得

式中的λi,k為Wk的特征值，相應的正交矢量為ui,k.令ξi,k滿足

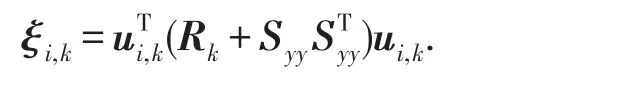
由于λi,k≥0，并且ξi,k≥0，則可以得到

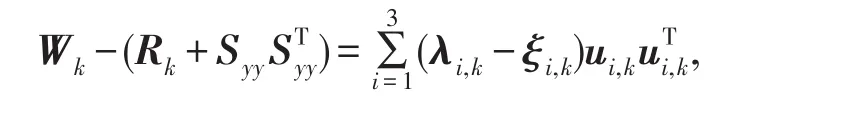
則最終的最適應算法為

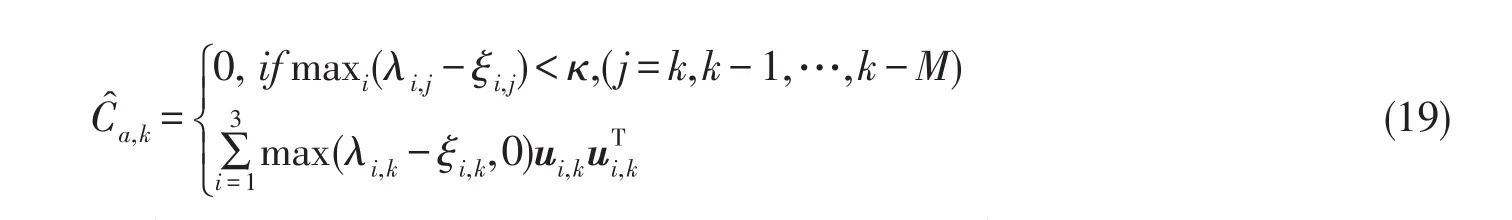
上式中的判斷窗口M以及閾值κ均是為了確保能夠計及由于加速度計自身的測量噪聲對機動加速度的估計產生的影響，將估計的加速度值在加速度計的測量中進行補償即可實現自適應UKF融合估計姿態.

4 實驗結果與分析

實驗設備主要包括星網宇達公司的微機械慣性測量單元XW-IMU5220，參考系統為XW-ADU7612.其中IMU5220中包含有3個MEMS陀螺（零偏≤0.08°/s，零偏重復性≤0.05°/s，測量噪聲RMS≤0.05°/s）和3個MEMS加速度計，并且做了相應的溫度補償，能夠穩定地輸出100 Hz的測量值.參考系統XW-ADU 7612能以100 Hz的數據更新速率，給出被測對象精確的姿態角(航向角、俯仰角和橫滾角)，其航向角精度為0.1°，俯仰角和橫滾角的精度靜態時均達0.05°，動態時均可達0.1°.根據所用器件的靜態測量數據給定如下濾波器參數，預測時間0.01 s，更新時間0.1 s，過程噪聲和測量噪聲均為零均值白噪聲，過程噪聲方差分別為測量噪聲方差分別為

在校園進行了繞圈實驗，采集時間為267 s，由于實際更新頻率為100Hz，數據量較大，作圖時每1 s顯示一個數據.

圖1表示各傳感器姿態角單獨估計結果與對比.可以看出，以陀螺積分得到的姿態角明顯存在累積誤差；由于3軸耦合，航向陀螺在轉彎時數值較大，因此陀螺積分得到的俯仰角和橫滾角在轉彎階段，其累積誤差淹沒在航向耦合帶來的誤差中；采用加速度計計算的姿態角不存在累積誤差，但是噪聲較大，并且在有機動加速度時存在較大的偏差.按照坐標系定義，線加速度對俯仰角產生影響，向心加速度對橫滾角產生影響，在車起步和停車過程中以及轉彎過程中，采用加速度計單獨估計姿態角均有較大偏差.

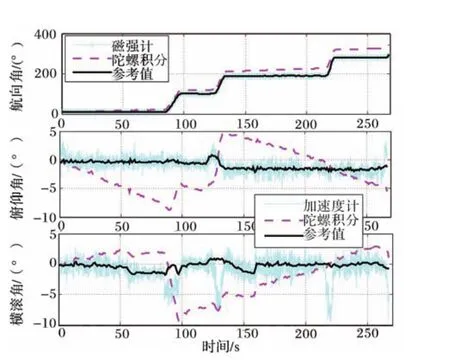
圖1 姿態角單獨估計結果與對比

圖2和圖3分別是俯仰角和橫滾角的UKF算法估計結果與對比.可以看出，采用UKF算法可以實現陀螺數據與加速度數據的融合，去除了采用加速度計單獨估計時的誤差，說明陀螺的短時精度與加速度計的長時精度相結合能夠得到較為精確的姿態估計；采用自適應UKF估計機動加速度并且進行補償之后，誤差明顯變小，基本上與參考姿態曲線重合，說明本文中提出的自適應UKF算法能夠有效地去除加速度計中的機動加速度干擾.圖4為自適應UKF算法估計得出的機動加速度，自適應參數選擇為N=10，M=10，閾值選擇為κ=0.1.

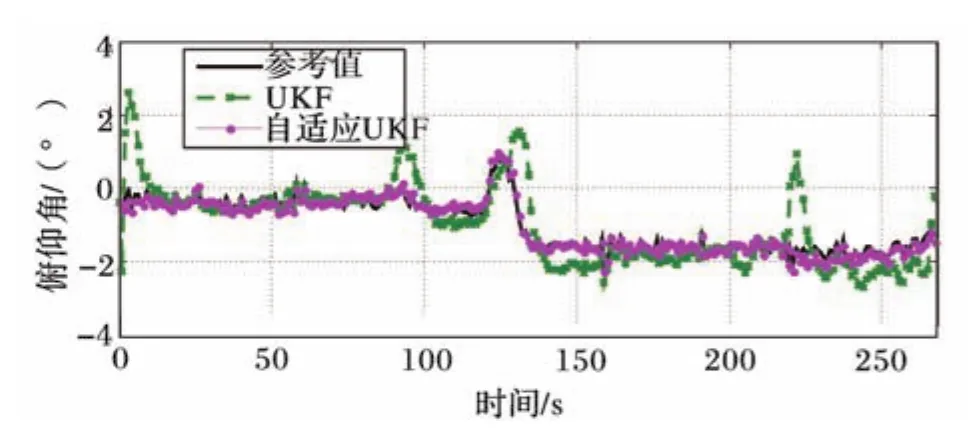
圖2 俯仰角UKF算法估計結果與對比

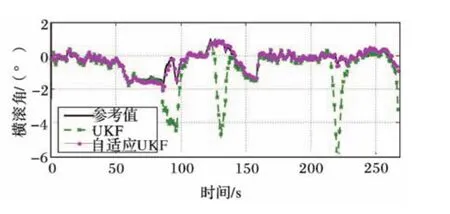
圖3 橫滾角UKF算法估計結果與對比

圖4中的線加速度與向心加速度估計結果分別與圖3中未采用UKF自適應算法時的俯仰角和橫滾角估計誤差相對應.圖5為姿態角自適應UKF算法的估計誤差.可以看出，航向角誤差絕對值在0.4°以內，俯仰角和橫滾角誤差絕對值均小于0.6°，滿足一般的車輛姿態估計精度要求.由于機動加速度對航向角的估計無影響，航向角估計依靠磁強計，圖5中給出了其估計誤差.

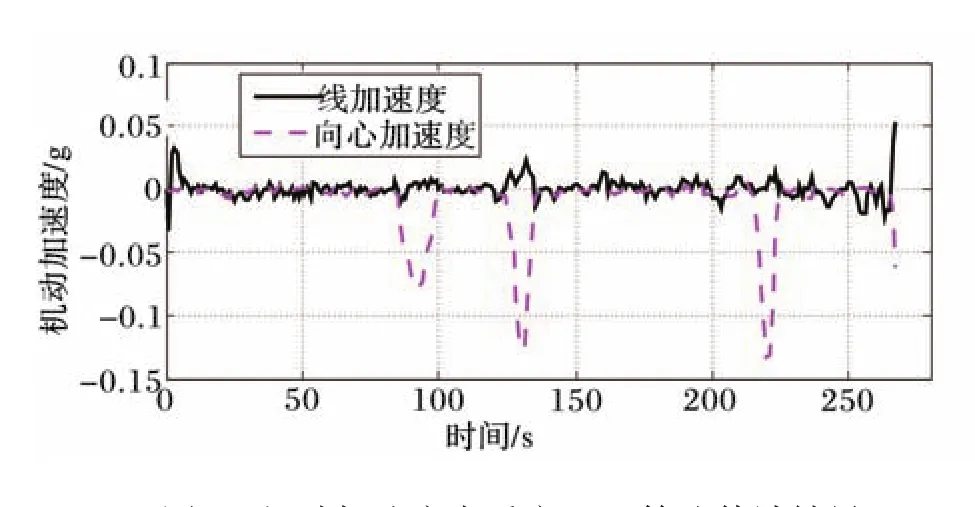
圖4 機動加速度自適應UKF算法估計結果

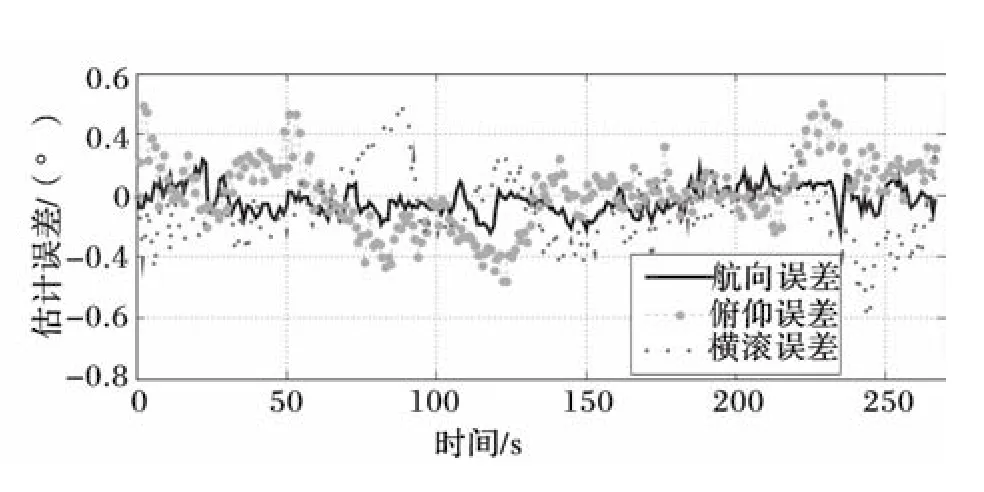
圖5 姿態角自適應UKF算法估計誤差

5 結論

本文中提出一種適用于車載環境的低成本航姿測量系統，采用3軸陀螺積分得到姿態角，同時利用加速度計校正水平陀螺零偏，利用磁強計保證航向角精度.針對加速度計測量姿態角容易受到非重力加速度的影響，本文中提出了一種自適應UKF算法，可實時估計并補償機動加速度對姿態角估計的影響.實際跑車實驗結果表明，提出的自適應UKF算法能夠得到較高精度的姿態角估計.此外，該低成本姿態測量系統還可用于車載穩定平臺、指向跟蹤系統以及小型無人機的姿態控制系統中.

[1]Beljour H，Coryell L，Tat F.Army SATCOM on the move technology initiatives[C]//IEEE Military Communications Conference.Boston，MA，2009:1-7.

[2]祝燕華，蔡體菁，楊卓鵬.MEMS-IMU/GPS組合導航系統的實現[J].中國慣性技術學報，2009，17(5)：552-556.

[3]沈曉衛，姚敏立，趙鵬.基于互補濾波的動中通天線姿態估計[J].中國慣性技術學報，2011，19(2)：194-197.

[4]Yun Xiaoping，Bachmann Eric R.Design，implementation，and experimental results ofa quaternion-based Kalman filter for human bodymotion tracking[J].IEEE Transactionson Robotics，2006，22(6):1216-1227.

[5]Henrik Rehbinder，Hu Xiaoming.Drift-free attitude estimation for accelerated rigid bodies[J].Automatica，2004，40:653-659.

[6]秦永元.慣性導航[M].北京：科學出版社，2006.

[7]Crassidis John L，Landis Markley F，Yang Cheng.Survey of nonlinear attitude estimation0methods[J].Journal of Guidance，Control，and Dynamics，2007，30(1):12-28.

[8]Julier SJ，Uhlmann JK，Durrant-whyte H F.A newmethod for nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactionson Automatic Control，2000，45(3):477-482.

[9]伍宗偉，姚敏立，馬紅光，等.移動衛星通信低成本多傳感器融合姿態估計方法[J].西安交通大學學報，2012，46(12):55-61.

[10]Crassidis John L，Landis Markley F，Yang Cheng.Applicaiton of magnetic sensors for low cost compass system[C].IEEE Plans，Position Location and Navigation Symposium，2000:12-28.