基于熵度量的屬性約簡算法研究

張繼洲 米志飛 謝春麗

摘要：為了減少故障參數的特征數量，加快診斷算法的運行速度，提高故障診斷的效率，本文提出利用熵度量理論對故障參數的特征按重要程度進行排序，將重要程度靠后的特征依次去除，計算去除某些特征后的特征集的熵變化量，若熵變化量變化比較小，則將該特征真正約簡，再從約簡后的特征集中選出一個最優的約簡特征集。利用自組織特征映射神經網絡對故障參數特征約簡結果進行檢驗，驗證結果表明：利用熵度量理論得出的約簡結果能夠用于故障診斷且診斷結果正確。

關鍵詞：熵度量；屬性約簡；故障診斷；SOM神經網絡

中圖分類號：S11；TP206+.3

文獻標識碼：A

文章編號：1001-005X（2015）04-0087-05

隨著儲存技術的快速發展，越來越多的故障數據被儲存，而故障診斷過程就是對這些海量般的歷史數據進行分類分析的過程。在診斷過程中，最重要的一步就是特征提取。為了更加準確的描述機器的工作狀態，大量的特征被創造出來并被用來描述機器設備的運行狀態。但是，數據的特征越多（維度越高），分析的難度越大，分析結果的可信度也越低。所以，必須對數據進行屬性約簡（特征約簡或者維歸約）。利用熵度量理論，能夠直接對特征的重要程度進行排序，可以有效降低故障診斷參數的維數、加快診斷算法的運算速度。

1 熵度量理論

已知初始特征全集 ，去除任意特征 得到一個特征集 ，特征集變化前后的熵的變量 越小，特征 對特征集F越不重要

根據文獻，設約簡集合 ，故約筒子集 的熵的重要度為

最簡約簡子集（集合中元素最少）定義為：

2 熵度量理論屬性約簡實例

根據熵度量理論，本文對電控發動機故障征兆集進行約簡，利用文獻中的部分故障與征兆對熵度量理論屬性約簡算法進行說明。

定義對象集（故障集） 屬性集（征兆集） ，各參量定義見表1和表2。

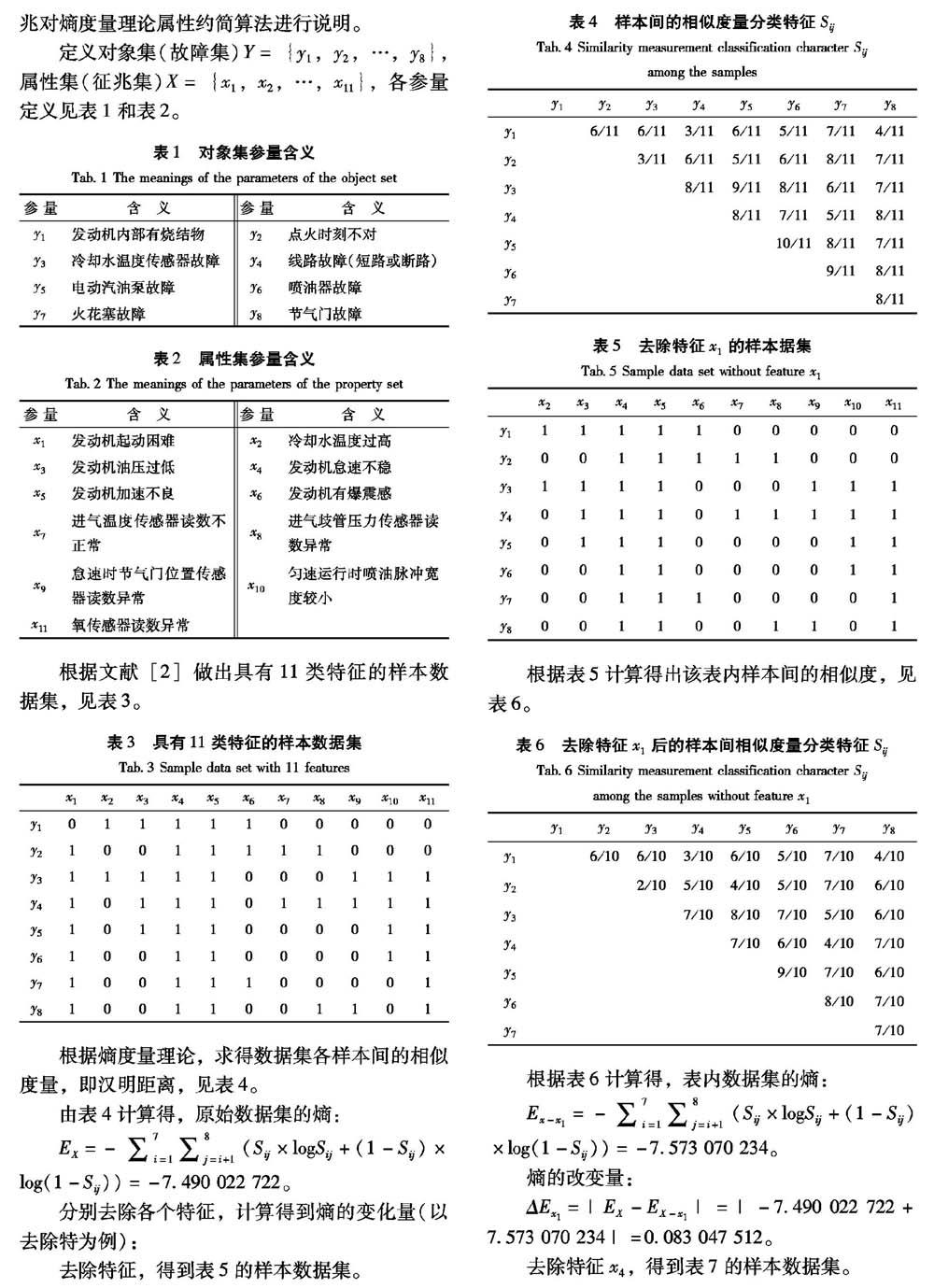
根據熵度量理論，求得數據集各樣本間的相似度量，即漢明距離，見表4。

由表4計算得，原始數據集的熵：

分別去除各個特征，計算得到熵的變化量（以去除特為例）：

去除特征，得到表5的樣本數據集。

根據表6計算得，表內數據集的熵：

熵的改變量：

去除特征X₄得到表7的樣本數據集。

根據表8計算得，表內數據集的熵：

熵的改變量：

以相同的方法計算求得：

根據熵的變化量可知，存在兩種約簡方案見表9。

采用方案一時，約簡特征X₄、X₅、X₆后，屬性集的熵為 ，約簡前后熵的改變量

采用方案二時，約簡特征X₄、X₅、X₆、X₁₁后，屬性集的熵為 ，約簡前后熵的改變量 。比較兩方案結果， ，根據熵度量理論，熵的改變量越大，該特征越重要，所以特征X₁₁對故障診斷的正確性和診斷速度影響更大，方案一更合適，即將特征X₄、X₅、X₆約簡，得到核心屬性X₁、X₂、X₃、X₇、X₈、X₉、X₁₀、X₁₁、。

3 約簡結果算法驗證

為驗證約簡結果是否可以用于實踐運用，本文利用SOM神經網絡對約簡結果進行驗證，驗證是否可以利用約簡得到的核心屬性識別出文獻中的8種故障類型。在驗證過程中，將約簡結果即X₁、X₂、X₃、X₇、X₈、X₉、X₁₀、X₁₁作為SOM神經網絡的輸入，文獻中的8種故障類型即y₁、y₂、y₃、y₄、y₅、y₆、y₇、y₈作為SOM神經網絡的輸出結果。神經網絡的理想輸入和輸出見表10。

將樣本1～8作為訓練樣本，對SOM神經網絡進行訓練，文獻中的故障現象數據見表11作為測試數據進行故障診斷，訓練結果和診斷結果見表12和表13（以樣本4和樣本7為例）。

由表12和表13可以看出，當訓練步數為100時，每個故障類型都被劃分為一類，分類非常細化，互不影響診斷結果。當訓練步數提高到200、500、1000時，分類結果沒有變化，對診斷結果已經沒有實際影響。在訓練好的網絡中，輸入樣本4和樣本7，診斷結果如上表12和表13所示，SOM神經網絡將樣本4分到故障類型y4，將樣本7分到故障類型y7中，故障診斷結果與實際故障原因相同，說明約簡后的屬性集可以用于故障診斷，且不影響故障診斷結果。

4 約簡結果實驗驗證

在算法驗證的基礎上，筆者在實驗室組建一個由可設置不同故障的測試車輛、X-431開放式汽車故障診斷儀組成的測試系統對約簡結果進行驗證。在8種故障分別存在的情況下進行測試，每種故障情況下測得20組數據，總共160組數據，從中隨機選出152組數據作為訓練樣本數據集，剩余8組數據作為測試數據集，構建一個8-17-8的BP神經網絡進行故障診斷。由圖1可知，當訓練迭代次數達到13次時，系統網絡的輸出達到要求誤差，結束訓練，輸入測試數據集進行測試，得到輸出結果，見表14。

由表14可以看出，實際輸出與理想輸出相吻合，說明約簡后的特征屬性集可以用于實踐中，再次表明本文的約簡方法的正確的、可用于實踐的。

5 結束語

本文利用熵度量理論，根據屬性約簡前后屬性集的熵的改變量大小對故障屬性的重要程度進行了排序并將不重要的特征挑選出來進行約簡，得到一個最簡約簡屬性集合。為了驗證該最簡屬性集是否能夠用于屬性約簡，本文利用SOM神經網絡從算法上對屬性約簡結果進行故障診斷驗證，利用BP神經網絡從實際測試中對約簡結果進行故障診斷驗證，驗證結果表明根據熵度量理論得出的最簡約簡屬性集合是合適的，能夠得到正確的診斷結果，達到了減少屬性特征且不影響診斷結果的目的。