基于特征線法的畦灌施肥地表水流溶質運移模型研究

李志新 許迪 李益農

摘要 為實現畦灌施肥技術參數的優化組合，建立合理的模型工具至關重要。基于零慣性量模型和一維對流彌散方程ADE作為畦灌施肥水流和溶質運移方程，分別利用有限差和特征線法進行求解，建立基于特征線法的畦灌施肥地表水流溶質運移模型。以隱式有限差解法為對照，對特征線法引入的數值誤差狀況進行評價。結果表明，相對于隱式有限差解法，采取特征線法求解ADE時引入的數值震蕩和數值彌散有顯著減少，基于特征線法的畦灌施肥地表水流溶質運移模型更合理。

關鍵詞 畦灌施肥；地表水流；溶質運移；對流-彌散；數值誤差

中圖分類號 S275.3；S153.5 文獻標識碼 A 文章編號 0517-6611（2015）05-084-04

Study on Model of Overland Water Flow and Solute Transport to Border Strip Fertigation Based on Characteristic Curve Method

LI Zhixing1， XU Di2， LI Yinong2

（1. School of Civil Engineering， Guizhou Institute of Technology， Guiyang， Guizhou 550003； 2. National Center of Efficient Irrigation Engineering and Technology Research， China Institute of Water Resources and Hydropower Research， Beijing 100044）

Abstract In order to realize the optimized combination of technical factors of border strip fertigation， it is necessary to establish a reasonable model tool. Based on zeroinertia model as flow equation solved by finite difference method， and 1D ADE as solute transport equation solved by characteristic curve method， a overland flow and solute transport model was established based on characteristic curve method. With finite difference method as contrast method， the numerical errors introduced by characteristic curve method were evaluated. The results suggested that when compared with finite method， the numerical errors introduced by characteristic curve method is obviously smaller， and the model of overland flow and solute transport based on the numerical errors introduced by characteristic curve method should be more reasonable.

Key words Border strip fertigation； Overland water flow； Solute transport； Advectiondiffusion； Numerical errors

基金項目 國家863計劃重點項目課題（2006AA100210）；國家科技支撐計劃重點項目課題（2006BAD11B02）。

作者簡介 李志新（1976- ），男，江西撫州人，博士研究生，研究方向：地面灌溉技術。

收稿日期 20141223

畦灌施肥是地面灌溉施肥的一種，預先將化肥充分溶解，并與灌溉水流，混合實施液體施撒的新型施肥方式[1-2]。與地面灌溉的傳統氮素化肥施用方式相比，這種施肥方式具有減少能耗、勞動力及其對土壤或作物的擾動破壞等優點[3]，在國外已得到越來越多的推廣應用[1-2]，在我國尚處于起步階段。但是，若缺乏合理的技術管理措施，該方法在施肥均勻性方面的效果不理想，還會產生肥料在土壤深層滲漏的問題[4]。因此，畦灌施肥研究通過探討施肥時機、入地流量、土壤入滲性能、微地形、坡度等重要技術要素對土壤水氮時空分布的影響[5]，為畦灌施肥系統優化設計管理提供指導。畦灌施肥技術要素及其組合范圍較寬泛。對技術要素組合方案進行計算、評價，需要通過數十或數百次的灌溉施肥模擬在較短時間內實現。因此，合理的模型是畦灌施肥系統中優化管理的理想工具。

Abassi等[6]在對地面灌施肥進行模擬研究中，以圣維南方程和一維對流彌散方程ADE作為模型水流和溶質運移控制方程，分別采用有限體積法和CrankNicolson格式隱式有限差進行求解，通過降低網格皮克里特數（Pe）克服對流項離散帶來的數值震蕩和彌散問題。結果表明，彌散度和輸入溶質的濃度對灌溉施肥均勻性的影響較小。值得指出的是，上述研究中在處理ADE中對流項離散帶來的數值震蕩和彌散問題時，采取降低Pe的方法，對于時空網格剖分有嚴格限制性要求，而實際中的研究對象時空網格剖分細化程度相當有限[7]。特征線法利用有限差求解ADE中彌散項，而利用質點追蹤Lagrange法求解ADE中對流項，最后將兩者組合起來，能夠有效地解決數值誤差問題，而在網格剖分上沒有限制[7-8]。

筆者以零慣性量模型和一維ADE作為畦灌施肥水流和溶質運移方程，分別利用有限差和特征線法進行求解，建立畦灌施肥地表水流溶質運移模型，并將特征線法與作為對照的隱式有限差解法引入的數值誤差狀況進行對比分析，以評價基于特征線法的畦灌施肥地表水流溶質運移模型的性能和合理性。

1 地表水流運動模型

1.1 控制方程及初始和邊界條件 采用的零慣性量模型是由完全水動力模型忽略加速度項簡化而來的[9]。

qt+qx+I=0

hx=SL-Sf

Sf=q2C2R3

C=1nR1/6（1）

式中，q為入畦水流在任一時刻的斷面單寬流量，m3/（min·m）；I為單位長度的入滲率，m3/（min·m）；SL為畦田縱坡；Sf為阻力坡降；h為任意時刻的田面入流水深，m；n為曼寧糙率；t為時間坐標，min；x為距離坐標，m；R為水力半徑，m。

初始條件：

h=0，q=0 （t=0）（2）

左邊界條件：

q=q0 （0

q=0 （t1

h=0，hx=0（t2

右邊界條件：

h=0 （0

q=0 （t3

式中，t1為畦口停水時間，min ；t2為畦口退水時間，min；t3為水流前鋒到達畦尾時間，min；t4為退水時間，min；xL為畦長，m；xa為水流前進鋒面到達位置，m；其他符號意義同前。

1.2 求解方法 對零慣性量模型采用有限差數值求解[10]。首先，構造其差分格式，單元格劃分在時間t軸上采用等步長，在空間x軸上采用不等步長，其值為第k時段δt內水流推進距離δxk，按此構造的單元為一四邊形單元，相應的差分方程為非線性方程組，可采用泰勒展開式線性化進行迭代求解（即牛頓迭代法）。求解參數有各結點水深、流量。

由基本模型的邊界條件可知，第一時段的水流推進距離與畦首水深不能用基本方程求解，因此根據初始條件與能量方程，建立如下方程組來計算。

q0t-δx1（h01+β+z01+α）=0（8）

βh0δx1+s0=n2q20h10/30（9）

式中，δx1為σt時刻的水流前鋒位置，m；β、α分別為反映地表水形狀的冪函數關系的指數和Kostiakov入滲公式中的指數（無量綱）；h0為畦首水深，m；其他符號意義同前。該式也是一非線性方程組，可采用牛頓迭代法求解。

2 地表溶質運移模型

2.1 控制方程及初始和邊界條件 對于條形畦田，畦田水流中溶質運移可用一維ADE方程[11]來描述。

（hC）t+（qC）x+Ci=x（hDxCx）（10）

式中，h為水深，m；C為溶質濃度，g/m3；t為時間，min；q為單寬流量，m3/（min·m）；x為縱向距離，m；i為入滲速率，m3/（min·m）；Dx為縱向彌散系數，m2/s。

初始條件：在計算區域內，給定初始溶質濃度分布，即

C（x，t0）=0 （x ∈[0 L]，t0=0）（11）

式中，x為畦長，m；t0為初始時刻，min；L為畦田總長，m；其他含義同前。

邊界條件：分別為給定濃度和給定通量的邊界條件，即

C（x0，t）=C0 （x0=0，t∈[0 T]）（12）

x（hDxCx）-（（qC）x+Ci）|x=L=qL（x=L，t∈[0 T]）（13）

式中，C0為畦首給定邊界濃度條件，g/m3；qL為畦尾給定溶質通量邊界條件，m3/（min·m）；其他含義同前。

2.2 求解方法

2.2.1 特征線法。對式（9）數值求解采用特征線法[7]。特征線法求解思路的特點是將溶質在水流中的對流和彌散分開，分別加以求解，然后疊加起來。溶質在水流中的運動可視為沿著水流方向以水流速度（u）運動的動坐標系中的純彌散問題。由于對流作用，運動質點攜帶初始濃度在一個時步（Δt）內運動了Δl=uΔt的距離，同時由于彌散作用，質點濃度改變了Δc，在Δl位置的溶質濃度為c=c0+Δc。該濃度又被視為下一個時步的初始濃度，還利用彌散作用結果對運動質點濃度進行修正。然后，可以轉入下一個時步的質點運動，并計算出該時步末各位置的溶質濃度。

求解具體步驟。首先，剖分研究域成等大小的網格，并放置一定數量的質點，質點的初始濃度由初始條件確定。對于時間步（Δtk+1），每個質點在水流的作用下都沿著速度方向運動一段距離，新的位置通過對下式的差分。

ux=dxdt（14）

得到新位置為：

xk+1p=xkp+Δxp=xkp+uxΔtk+1（15）

p=1，2，L，Np；k=0，1，2，L，Nt-1（16）

式中，xk+1p、xkp分別為質點p在k和k+1時間步的坐標位置；Np為質點總數；Nt為時間步數。

由于質點運動，網格中的質點及其濃度將發生變化。對于i 網格，由對流作用在k+1時間步流入此網格的各質點的濃度平均為Ck+1*i，j。

在確定對流作用引起的濃度改變后，考慮彌散作用、源匯作用等對濃度改變的貢獻，可由下式特征線微分方程確定。

dCdt=1nbxi（nbDijCxj）+F（17）

通過對以上方程的差分，可得到彌散作用和源匯作用等所引起的濃度改變。

ΔCk+1i，j=（ΔCk+1i，j）1+（ΔCk+1i，j）2（18）

因此，在得到對流引起的濃度改變Ck+1*i，j和彌散作用、源匯作用等所引起的濃度增量ΔCk+1i，j后，可得到對流彌散方程的解。

Ck+1i，j=Ck+1*i，j+ΔCk+1i，j（19）

2.2.2 對照的隱式有限差解法。作為對照的隱式有限差解法主要包括空間域離散、空間一階和二階導數的差分、時間域離散、邊界條件施用、差分方程組求解等步驟[6-7]。首先，將一維線形研究域剖分成網格，即差分網格，網格線交點稱為格點，網眼稱為網格，計算點稱為節點。差分法則以網格中央作為計算節點建立差分方程；在此基礎上，微分方程式（9）中的一階、二階導數用中央差分形式來表示；通過時間域離散，將時間域進行等分，每個部分稱為時間步或簡稱時步，用k來計數，每個部分的長度稱為時間步長；時間域離散之后，求t時刻數值解的基本思想是用本時間步k的已知值Ck來計算下一個時間步k+1的濃度Ck+1，使用第j個網格k+1時間步的濃度Ck+1j代替 Cj，得到微分方程式（9）的FTCS隱式差分格式，進而形成以Ck+1j（j=1，2，…，Nx）為未知數的方程組；在施以邊界條件后，上述線性方程組未知量個數和方程個數相等，均為Nx個，可表示為：

[a][c]={b}（20）

式中，[a]為系數矩陣；[c]為待求濃度列向量；{b} 為右端項列向量。對上述方程組求解程序在MATLAB環境下采用直接解法——追趕法實現。

3 結果與分析

為了對上述2種數值解法在強對流條件下求解ADE中所引入的數值誤差（數值震蕩和數值彌散）進行分析對比，對一個測試問題分別進行解析求解和數值求解，解析解作為比較基準，其中數值求解分別采用隱式有限差和特征線法，隱式有限差作為對照數值解法。通過將每種數值解法求解結果分別與解析解結果對比，可以評價分析各中數值求解方法引入的數值誤差，進而對數值解法之間的數值誤差及其方法優劣進行對比分析，以評價特征線求解法的性能和合理性。

3.1 測試問題 測試問題假定溶質運移是在一個等速均勻水流流場中進行的，且在初始時刻水中無任何溶質分布，在初始時刻開始一端連續注入濃度為C0的保守性示蹤劑，溶質的對流擴散是一維的，相關數學模型[7]如下：

Ct=D2Cx2-uCx 0≤x≤+∞，t>0（21）

初始條件：C（x，t）|t=0=0 0≤x≤+∞（22）

邊界條件：C（x，t）|t=0=C0

limx→+∞C（x+t）=0 t>0（23）

式中，C為溶質濃度，g/m3；D為彌散系數，m2/min；x為沿畦長坐標，m；u為水流流速，m/min；t為時間，min。

3.2 解析與數值求解

3.2.1 解析解。通過Fourier變換，可求得上述定解問題的解析解[7]。

C（x，t）=12C0[erfc（x-ut4Dt）+exp（x+ut4Dt）erfc（x+ut4Dt）]（24）

式中，erfc（x）為余誤差函數；其他符號意義同前。

3.2.2 數值解。數值求解方法分別采用特征線法和作為對照的隱式有限差方法。數值求解輸入參量有：研究域長度80 m，空間剖分單元數（Nx）=200，模擬時段為25 min，時步數（k）=200，水流速度（u）=3 m/min，注入溶質初始濃度C0為5 g/m3。

溶質運移參數彌散系數（Kx）用以下公式[10]計算：

Kx=CeCdngh5/6v（25）

式中，Ce為常數（無量綱）；h為水深，m； v為流速，m/min；n為糙率；g為重力加速度，N/kg；Cd為常數，m0.5/min。文中Ce取值為4，n為0.11，Cd為60 m0.5/min。

3.2.3 求解方法數值誤差對比分析。

一個完整的數值模型由控制方程、定解條件和求解方法構成。在控制方程和定解條件既定的條件下，數值求解方法的不同影響模型的精度及其優劣。該文在相同時空域網格剖分及其他模型輸入參數相同的條件下，對采用的特征線法和隱式差分法引入的數值震蕩和數值彌散大小進行比較分析，以評價強對流條件下求解地表溶質運移方程ADE采用特征線法的合理性。

作為比較基準解析解結果沒有任何數值震蕩和數值彌散，而數值解則由于數值近似存在數值震蕩和數值彌散，因此分別將特征線法和隱式有限差的求解結果與解析解結果對比，分析各自引入的數值誤差狀況。最后，就各自引入的數值震蕩和數值彌散進行對比，以評價特征線法相對于對照解法的性能及合理性。

（1）特征線法。

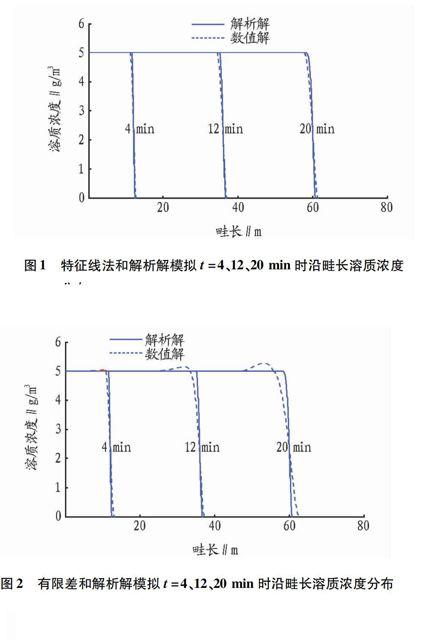
圖1為特征線法與解析解模擬在時刻t=4、12、20 min時沿畦長的地表水流中溶質濃度分布狀況。由圖可知，特征線法與解析解模擬結果吻合性很高，因此特征線法引入的數值誤差（包括數值彌散和數值震蕩）很小，有效克服了強對流條件下的數值震蕩和數值彌散問題。在t=12、20 min的過渡帶（陡坡）曲線上，數值解曲線坡度略有放緩（比解析解結果曲線減少的坡度即是數值方法本身引入的數值彌散造成的，解析解過渡帶曲線的坡度才是由物理彌散系數（D）的真實反映）。由此可知，隨著時間的推移，特征線法求解結果的數值彌散變得更明顯，但總體上數值彌散量仍很小；特征線法模擬結果曲線單調下降，平滑而無任何起伏，說明該解法不存在數值震蕩問題。

（2）隱式有限差方法。

圖2為隱式有限差方法與解析解模擬在時刻t=4、12、20 min時沿畦長的地表溶質濃度分布狀況。由圖可知，隨著時間的推移，數值解曲線過渡帶坡度與解析解結果差異變得更加明顯，尤其是t=20 min時曲線，數值彌散現象較明顯，這是數值誤差的時間效應形成的；數值解在溶質濃度由高變低的突變處有較大的數值震蕩現象，與數值彌散現象相似，數值震蕩隨著時間推移明顯增大。由此可知，隱式有限差解法存在的數值震蕩現象較明顯，同時引入一定的數值彌散。

通過對特征性法和隱式有限差方法間數值誤差的對比分析，可知特征線法求解引入的數值誤差很小，存在輕微的數值彌散，而沒有數值震蕩現象；而隱式有限差會產生較明顯的數值震蕩現象，同時隱式有限差引入的數值彌散也較特征線法明顯。因此，在求解畦灌施肥地表溶質運移方程ADE時，采用特征線法進行數值求解較合理，能夠有效地解決強對流條件下數值求解引入的數值震蕩和數值彌散問題。

4 結論

基于零慣量模型和一維ADE分別作為水流和地表溶質運移控制方程，利用有限差和特征線法進行數值求解，建立一維畦灌施肥地表水流溶質運移模型。特征線法和對照解法隱式有限差解法間的數值誤差對比分析表明，特征線法能夠更有效地解決數值震蕩和數值彌散問題，而隱式有限差方法則引入較大的數值震蕩和數值彌散，數值震蕩現象尤其突出，而且特征線法是借助于Lagrange方法求解對流項而克服數值誤差，而隱式有限差方法減少數值誤差必須通過細化網格剖分，在實際應用中網格細化剖分卻往往受到限制。因此，采用基于特征線法的地表溶質運移模型顯然更合理。

參考文獻

[1] SANTOS D V，SOUSA P L，SMITH R E.Model simulation of water and nitrate movement in a levelbasin under fertigation treatments[J].Agriculture Water Management，1997，32（3）：293-306.

[2] DILLION J，EDINGERMARSHALL S，LETEY J.Farmers adopt new irrigation and fertilizer techniques[J].California Agriculture，1999，53（1）：24-28.

[3] ZERIHUN D，SANCHEZ C A，FARRELLPOE K L，et al.Performance indices for surface N fertigation[J].Journal of Irrigation and Drainage Engineering，2003，129（4）：173-184.

[4] PLAYAN E，FACI J M.Border fertigation：Field experiments and a simple model [J].Irrigation Science，1997，17（4）：163-171.

[5] GARCIANAVARRO P，PLAYAN E，ZAPATA N.Solute transport modeling in overland flow applied to fertigation[J].Journal of Irrigation and Drainage Engineering，2000，126（1）：33-44.

[6] ABBASI F，SIMUNEK J，VAN GENUCHTEN M TH，et al.Overland water flow and solute transport：model development and fielddata analysis[J].Journal of Irrigation and Drainage Engineering，2003，129（2）：71-81

[7] 王洪濤.多孔介質污染物遷移動力學[R].北京：清華大學，2005.

[8] 李韻珠，李保國.土壤溶質運移[M].北京：科學出版社，1997.

[9] STRELKOFF T.SRFR20.51：A computer program for simulating flow in surface irrigation furrowsbasinsborders[R].USDAARS，Water Conservation Lab.，1993.

[10] ZERIHUN D，SANCHEZ C A，FARRELLPOE K L，et al.Performance indices for surface N fertigation[J].Journal of Irrigation and Drainage Engineering，2003，129（4）：173-184.

[11] ZERIHUN D，FURMAN A，WARRICK A W，et al.Coupled SurfaceSubsurface Solute Transport Model for Irrigation Borders and Basins.I.Model Development[J].Journal of the Irrigation and Drainage Engineering，2005，131（5）：396-406.

責任編輯 劉月娟 責任校對 李巖