基于批量遞歸最小二乘的自然Actor-Critic算法

王國芳,方 舟,李 平

（浙江大學航空航天學院,浙江杭州310027）

基于批量遞歸最小二乘的自然Actor-Critic算法

王國芳,方 舟,李 平

（浙江大學航空航天學院,浙江杭州310027）

為了減輕Actor-Critic結構中智能體用最小二乘法估計自然梯度時的在線運算負擔,提高運算實時性,提出新的學習算法：NAC-BRLS.該算法在Critic中利用批量遞歸最小二乘法估計自然梯度,根據估計得到的梯度樂觀地更新策略.批量遞歸最小二乘法的引入使得智能體能根據自身運算能力自由調整各批次運算的數據量,即每次策略估計時使用的數據量,在全樂觀和部分樂觀之間進行權衡,大大提高了NAC-LSTD算法的靈活性.山地車仿真實驗表明,與NAC-LSTD算法相比,NAC-BRLS算法在保證一定收斂性能的前提下,能夠明顯降低智能體的單步平均運算負擔.

自然梯度；Actor-Critic；批次更新；遞歸最小二乘

強化學習（reinforcement learning,RL）是最優控制和人工智能領域倍受關注的方法之一.和常規的監督學習及非監督學習不同,強化學習是將智能體放置于完全未知的環境中,智能體通過與環境相互作用,獲得可評估的即時報酬；根據即時報酬來優化自身的行為策略,從而獲得能夠最大化累積報酬的策略［1］.強化學習最明顯的優勢在于學習與模型無關并且適用于非線性乃至隨機控制問題,近年來,在復雜的智能機器人控制領域已獲得了可觀的應用成果［2-3］.

就算法結構而言,強化學習方法大體可以分為3類,即Actor-Only、Critic-Only和Actor-Critic（此處Actor表示動作選擇即策略,Critic表示策略評估）［3］.Actor-Only結構如REINFORCE法可以處理連續的動作,并且容易證明算法的收斂性,但由于缺乏策略評估過程,得到的策略梯度方差大,收斂速度會較慢［4］；Critic-Only結構如Sarsa及Q學習等通過值函數推導出策略,但僅適用于有限動作空間的情況,而且當狀態空間連續,值函數需要使用函數近似表示時,收斂性不能得到保證［5］；Actor-Critic結構能夠結合以上兩者的優點,目前研究相對較多,本文即是針對這種結構.

在多數Actor-Critic結構的算法中,Critic使用基于bootstrapping的瞬時差分來計算策略期望報酬［6］,然后Actor根據Critic推導出的期望報酬對策略參數的梯度來更新策略.這種方法的運算復雜度相對較低,適合在線學習.在Critic中使用瞬時差分,數據僅利用一次,然后就被遺棄,沒能充分挖掘數據包含的信息［7］.特別是在某些情況下,獲取數據消耗時間或者代價很大（比如飛行器的控制）,這需要強化學習算法盡量減少所需的數據量.隨著硬件性能的提升,計算機的運算速度不斷提高,瞬時差分學習方法在計算效率方面的優勢不太明顯,這為在計算復雜度和數據有效性之間作出更好的平衡提供了物理實現基礎.

Bradtka等［8］提出Critic使用基于線性值函數近似的最小二乘瞬時差分方法來評估策略.隨后, Boyan把資格跡（eligibility trace）引入到最小二乘瞬時差分（LSTD）中來提高泛化性能［9］.除數據高效利用外,LSTD避免TD學習算法中學習步長設計的困難,因而最小二乘法被認為是最好的策略估計方法之一［10-12］.與此同時,為了降低LSTD的計算復雜度,Xu等［13］引入遞歸最小二乘（RLS）法.

對于Actor,Amari［14］證明在某些情況下更新自然梯度更高效.隨后,Peters等［2］把自然梯度引入到Actor-Critic方法中,通過克服期望報酬對策略參數梯度小的困難直接指向最優策略來減少迭代次數,但估計自然梯度的運算復雜度比估計普通梯度大很多.

針對上述問題,本文提出在Critic中使用批量遞歸最小二乘法來計算自然策略梯度,從而有效地降低智能體單步平均運算復雜度,同時批量的引入可以增大最小二乘法在強化學習中使用的靈活性.智能體能夠根據實際運算能力調整每個批次的數據量,批次與批次的數據量不一致亦可,然后全樂觀（每個數據后都進行策略更新）或部分樂觀（一些數據后進行策略更新）［15］地更新策略,而不是在等得到準確的梯度估計或者完成一個episode之后［2］.該方法結合了自然策略梯度的快速收斂和遞歸最小二乘法的數據高效利用,能夠較快地獲得最優或次優策略,同時滿足智能體運算效率的限制,提高了最小二乘法估計自然梯度的實用性.

1 自然Actor-Critic

1.1 MDP模型

在強化學習中,需要解決的底層控制問題通常是序貫決策問題（sequential decision problem）,也稱作馬爾可夫決策過程（Markov decision process, MDP）.MDP問題通常包含（S,A,P,R,γ）5個元素,其中γ表示智能體對報酬進行處理的折扣因子；在t＝0時刻,智能體從初始狀態s0∈S出發；在離散t時刻,智能體觀測當前狀態st∈S,然后依據參數化策略π（at｜st,θ）選擇并執行動作at∈A,系統根據p（st＋1｜st,at）模型轉移到新狀態st＋1,給出即時報酬rt＝r（st,at,st＋1）［16］.

在實際問題中,狀態空間大都是連續的,狀態值函數Vπ（s）、狀態-動作值函數Qπ（s,a）、優勢函數（advantage function）Aπ（s,a）和策略π須使用函數來近似,值函數的線性表示可以定義為

強化學習的目標是找到以θ為參數的近似策略π（a｜s,θ）,使得從初始狀態出發,執行該策略能夠最大化每個狀態的折扣累積報酬值.

1.2 Actor-Critic

在Actor-Critic結構中,如圖1所示,策略（Actor）參數θ根據策略期望報酬對于θ的梯度方向進行更新.

假設ρ（π）表示策略π的長遠期望報酬,根據策略梯度定理可知,策略對于參數θ的常規或者“vanilla”梯度［17］表示為

式中：φ（s）表示在狀態空間中選取的基函數,φsa為狀態-動作值的基函數,為簡便起見,可以選取：

圖1 Actor-Critic框架Fig.1 Actor-Critic Framework

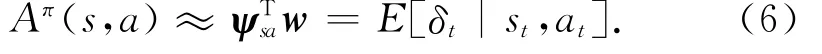
式中：w為近似優勢函數的參數.

函數近似的均方差可以通過下式計算：

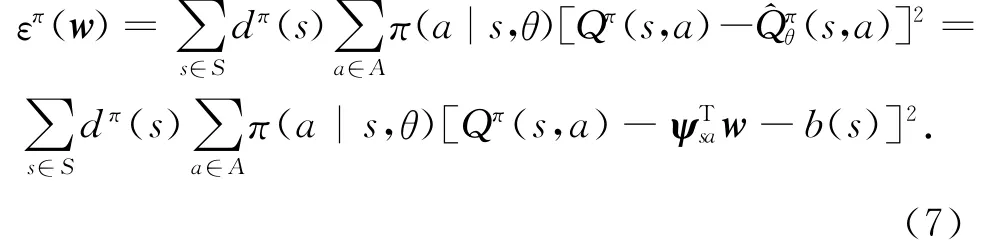
則優勢函數可以表示為

Bhatnagar證明：當bπ（s）＝V（s）時,均方誤差達到最小［5］,則參數的梯度可以表示為

將式（6）代入式（8）,推導出參數更新公式：

式中：αt、βt為參數更新步長,但兩者需要滿足一定的條件算法才能收斂.

1.3 自然Actor-Critic(NAC)

根據Peters等［2］所述,Actor-Critic中使用自然梯度更新策略能夠加快收斂速度.自然策略梯度是將策略結構信息引入到梯度中,可以通過普通梯度乘以費舍爾信息矩陣獲取.

策略的費舍爾信息矩陣定義如下：

式中：

即自然策略梯度是近似優勢函數的參數w［5］.

最終策略參數更新如下：

2 NAC-BRLS

2.1 基于最小二乘瞬時差分的NAC

在Critic中使用最小二乘瞬時差分來估計自然策略梯度,利用自然策略梯度來更新策略參數.本文只需設計策略參數更新步長,步長的收斂條件降低.

最小二乘估計問題的目標可以記作

式中：zn為資格跡,δn為瞬時差分誤差.

使用最小二乘法計算自然梯度,需要把自然梯度參數引入到最小二乘目標函數中.根據貝爾曼等式以及優勢函數的定義,可得

將式（1）、（6）代入式（15）,可得

在函數近似中,不可能每一點都完全滿足等式,因此δ（st,at,st＋1）表示誤差項.

將瞬時差分誤差表示為參數w、v的函數：

將式（17）代入式（14）,可以把目標函數表示為以w、v為變量的函數：

式中：

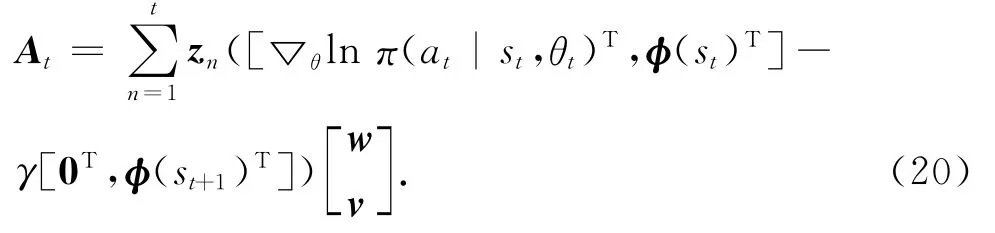
可以計算得到

2.2 基于批量遞歸最小二乘的NAC

計算矩陣At的逆矩陣需要o（n3）運算復雜度,其中n為矩陣At的階數.假設狀態基函數個數為x,智能體可以采取的動作數為y,則當只需要估計值函數參數v時,n＝x；當需要估計自然梯度w時, n＝（y＋1）x,計算復雜度增大為原來的（y＋1）3倍,尤其是當動作空間y比較大的時候,用LSTD在線計算是對智能體實時運算能力的極大考驗.

Ljung等［19］的矩陣逆法可以將計算復雜度降為o（n2）,將之用于求At［13］,能夠提高運算實時性.強化學習處理問題,有時數據是批次獲取的,因而需要使用矩陣逆法則的拓展形式.

假設每次使用m個數據進行梯度更新,則

此處資格跡為拓展的資格跡,每步更新方法不變：

由于資格跡zt中的遺忘因子λ中已經包含數據的權值因素,本文沒有對數據進行重新賦權重.

式（22）～（24）中,假設Ft＝,F0＝ρI, Kt＋1＝Ft＋1Zt,其中ρ為一個正數,I為單位矩陣.在式（21）中使用矩陣逆法則,可得

Moustakides證明,使用矩陣逆法則的時候,初始方差矩陣F0的額外參數ρ對收斂速度有重要的影響［18］,具體初值要根據經驗來選取.

隨著m的增大,雖然批量最小二乘法的單次運算復雜度相對m較小時有所提高,但批量數據量相對較小時,復雜度的增加不甚明顯；由于迭代次數減少,平均單步運算壓力明顯降低,批量運算的引入使得數據量能夠適應智能體運算能力,提高了計算的實時性.

策略更新步長的設置需要合適,過大的話可能發散,過小的話收斂比較慢.單次批量數越大,獲得的梯度估計可信度越高,相應策略更新步長可以適度增大,因而盡管迭代次數減少,但是性能基本不受大的影響.

2.3 NAC-BRLS算法的完整流程

1）初始化.設計值函數的基函數φ（s）和隨機策略π（a｜s,θ）,推導出優勢函數的基函數ψsa＝▽θlogπ（s,a）、參數陣θ＝θ0、v＝v0、w＝w0、折扣因子γ、遺忘因子λ、方差矩陣ρ和收斂誤差ε、批次數據量m.

2）選取起始狀態s0～p（s0）,l＝0.

3）選擇并執行動作at～π（at｜st,θt）,觀察下一個狀態st＋1～p（st＋1｜st,at）和報酬值rt＋1＝r（st,at, st＋1）.

4）若s＋1是終止狀態,則返回2）,zt設定為0；否則,式（24）更新資格跡.

若t＝（l＋1）m,則利用式（25）～（27）計算自然策略梯度,根據式（13）更新策略,l＝l＋1.否則存儲當前狀態值,Zt＝［Zt,zt＋1］,

5）若‖θt＋1－θt‖≤ε,則結束；否則返回3）.

3 模擬驗證

山地車（mountain car）上坡問題是強化學習領域常用的驗證實例.本文將提出的NAC-BRLS算法應用在山地車的控制學習中進行評估,并與NACLSTD、AC-LSTD和AC-RLS等經典算法進行性能對比.

3.1 山地車上坡問題

在山地車上坡問題中,智能體引導一輛欠驅動的汽車沿著斜坡盡快爬到位于一定高度的目標點,如圖2所示［20］.

困難之處在于汽車的牽引力不足,在某些位置牽引力分量甚至小于重力分量,因而不能從初始位置開始直接加速爬上山坡,需要先爬到對面的斜坡,然后利用重力加上牽引力來沖上對面更高的位置,如此反復才有可能到達目標位置.

假設選取車的水平位置x和水平速度˙x作為狀態空間,則狀態屬于連續型,值函數以及策略需要使用函數來近似表示.可以選擇的動作有3個,分別是a＝－0.2、0、0.2,具體數值可能包含幅值為0.04的白噪聲.

系統仿真動態模型為

式中：w＝0.2 kg表示車的質量,k＝0.3為黏滯系數,仿真步長Δt＝0.1 s；bound表示限制2個狀態的取值范圍－1.2≤xt＋1≤0.5,－1.5≤≤1.5.當山地車到達左邊界時,xt＋1不變,重置為0；當山地車到達右邊界時,目標達到,周期結束.到達目標點報酬為＋1,否則報酬為－0.01.最大化報酬是使山地車能夠最快地到達目標位置.

圖2 山地車問題Fig.2 Mountain car problem

在二維連續狀態空間上可以采用3×4的格子形成12個徑向基函數來近似值函數,得到

式中：μ表示徑向基函數的12個基準點｛－1.2,＋0.35,＋0.5｝×｛－1.5,－0.5,＋0.5,＋1.5｝.方差統一選擇σ2＝1,盡管這不一定是最優選擇［21］,但是該選擇是可行的,并能夠由此得到狀態-動作值函數和策略.

3.2 模擬結果及分析

分別使用不同批量運算數的NAC-BRLS算法、NAC-LSTD算法、AC-LSTD和AC-RLS算法學習訓練山地車,給出相應的仿真結果,并比較學習性能.

在模擬過程中,初始狀態s0＝［－0.5,0］,但包含幅值為0.1的白噪聲,折扣系數設為γ＝0.99,遺忘因子設為λ＝0.4,結束條件設為ε＝10－8,初始方差矩陣設為ρ＝2.對于NAC-BRLS方法,取批量運算數m＝1,2,3,4,5,7,9總共7種情況進行對比,觀察性能隨m變化的過程,統一設置策略更新步長β＝50m／（1000＋step＋n）.NAC-LSTD設定步長為β＝50／（1000＋step＋n）,AC-LSTD和AC-RLS設置步長為β＝100／（1000＋step＋n）,為了避免出現奇異值并且和遞歸方法保持一致,LSTD中選取起始At＝0.5I,step為在周期內的步數,n為周期的序數.雖然選定的策略更新步長不一定是最優的,通過不斷調整可以獲取更好的更新步長,但算法的對比是有效的.另外,為了減小偶然性誤差,每個算法都運行10次,然后取平均值作為評估性能.

每運行完一個周期后,對所得策略進行評估,獲取該策略性能.為了提高仿真效率,除小車到達目的地外,若某個周期模擬超過800步,則認為該策略是失敗的,不用再繼續進行評估.由于智能體的目標是盡快將山地車引導到某一個高度,可以選擇每個周期所需的步數作為策略性能指標,同時報酬函數應和步數一致.

4種學習方法的性能和效率對比如圖3～8所示.圖中,T為周期,R為報酬,t為耗時.

圖3、4給出本文算法（m＝1）與較常見算法的性能及報酬對比,2種指標的表示含義基本一致.與NAC-LSTD相比,NAC-BRLS獲得的仿真效果相近；與AC-RLS和AC-LSTD相比,盡管NACBRLS的更新步長較小,但收斂速度快很多,這說明自然策略梯度的引入能夠明顯地加快算法收斂速度.4種方法收斂的穩態基本趨于一致,說明4種方法都是可行的,最終都能夠達到相近策略.

圖3 不同方法的性能對比Fig.3 Performance comparison of different methods

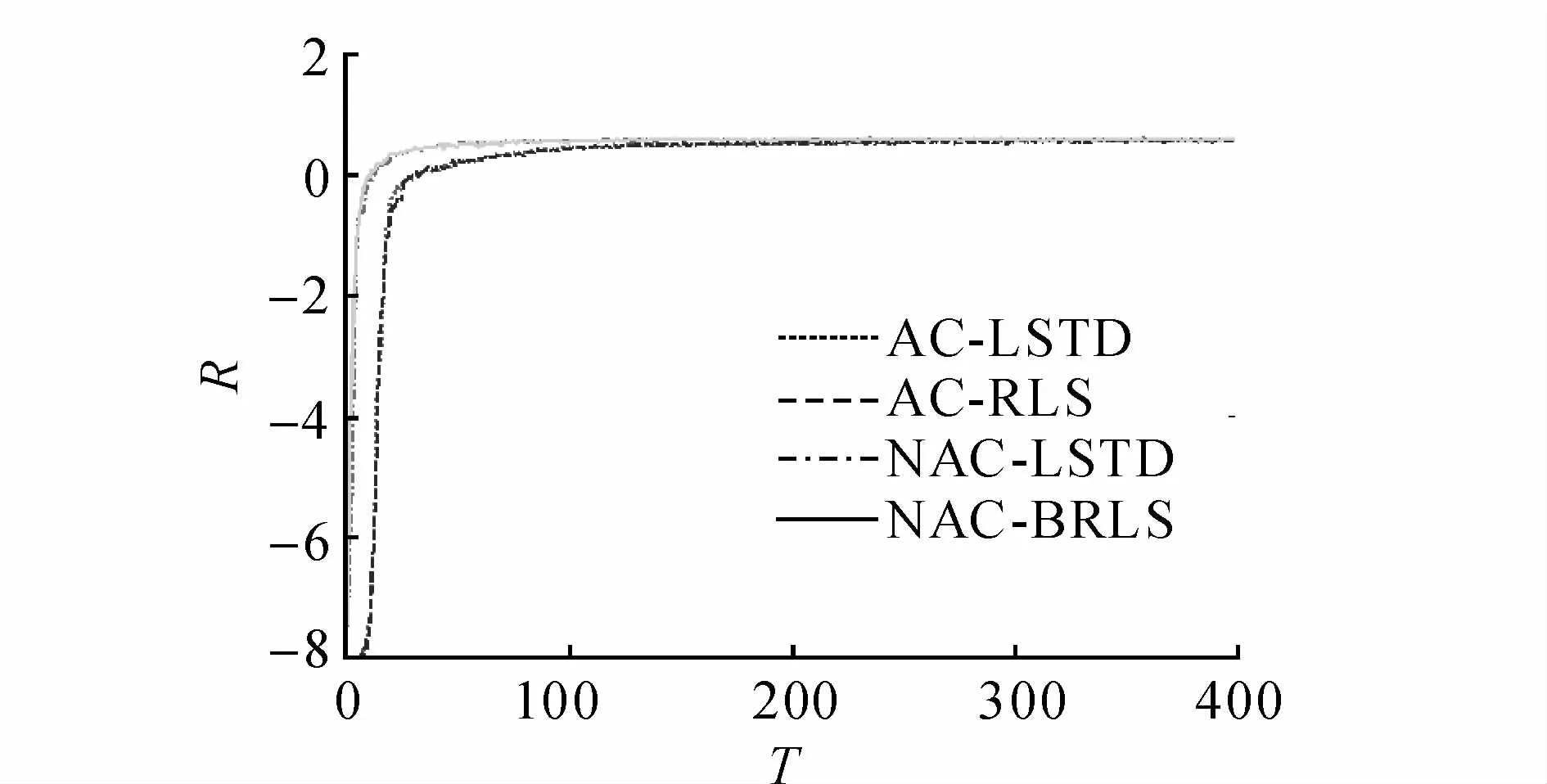
圖4 不同方法的報酬對比Fig.4 Rewards comparison of different methods

在性能上,NAC-BRLS與NAC-LSTD的效果相近,圖5對比了圖3、4所示方法的單步運行時間（單步運算時間來表示智能體的運算復雜度,此處時間是在i7處理器的電腦中matlab2012運行的結果）,批量遞歸引入的優勢很明顯.自然策略梯度的引入,使得最小二乘法即NAC-LSTD的單步運行時間較長,是AC-LSTD的2倍多,特別是當動作空間增大時,運算復雜度更大,實時性大大降低,對于高頻率的控制可能不適用,而NAC-BRLS能夠明顯降低單步平均運算耗時,提高了運算實時性.在ACLSTD中引入遞歸最小二乘,單步平均運算時間降低不明顯,原因在于求逆矩陣本身階次較低,因而策略更新等其他步驟的耗時相對較多.

算法的運行性能及報酬隨m變化的效果如圖6、7所示.以設定的策略更新步長來學習,當m較小時,收斂速度較快,但學習進行400周期之后,性能趨于一致.這說明批量遞歸最小二乘的性能對m變化的魯棒性較強,尤其是最終的收斂性能基本一致.

圖8給出NAC-BRLS中不同情況下的單步運行時間,即實時性的對比可知,AC-LSTD中使用LSTD估計普通梯度時階次低,運算時間相對較短,實時性高；雖然現在很多研究都已經引入遞歸最小二乘法,但運算時間降低不明顯.

圖5 單步耗時對比Fig.5 Time cost comparison of per step

圖6 不同批量數的性能對比Fig.6 Performance comparison of different batches

圖7 不同批量數的報酬對比Fig.7 Rewards comparison of different batches

圖8 不同批量數的時間對比Fig.8 Time comparison of different batches

Critic中使用LSTD估計自然梯度,運算時間顯著增大,更顯出使用遞歸的必要性.隨著m的增大,智能體單步平均耗時下降,實時性提高.特別是當m較小時,效果更明顯,但m增大,時間的降低效果不再明顯,甚至趨平.這是由于批量遞歸運算同樣引入了求矩陣逆運算,即m階矩陣求逆,當m較小時,運算復雜度o（m3）相對o（n2）較小,因此整體運算復雜度增加不大,但運算次數減少,平均單步耗時的降低比較明顯,當m＝2時,單步運算復雜度已經低于AC-RLS.當m過大時,m階矩陣求逆的計算復雜度大大增加,在遠超過n的時候,批量運算壓力可能會更大,這一點有待驗證.

3.3 合適批量數的討論

表1用數字對比了不同m值情況下算法的耗時、收斂性能及總報酬.當剛開始m增大時,單步耗時降低明顯,但對性能影響不大；隨著m的增大,收斂速度減慢比較明顯,但是時間上降低不多.若智能體運算能力差,則選取較大的批量值m,雖然收斂性能上有所降低,但能夠保證運算的實時性,實現在線學習,這是一種運算效率和收斂性能之間的平衡,需要根據具體情況選擇批量數.若AC-RLS可以在線學習,但需引入自然梯度來加快學習速度,則可以選取批量數m＝2,其單步運行時間已經低于AC-RLS算法,因而NAC-RLS算法能夠在線運行.

表1 不同m值對應的時間和性能對比Tab.1 Comparison of time and performance by different m value

4 結 語

本文針對Actor-Critic結構的強化學習,提出在Critic中使用批量遞歸最小二乘法來估計自然策略梯度.利用自然策略梯度樂觀地更新策略,這樣可以在充分利用數據包含的信息前提下,降低平均單步運算耗時,提高運算實時性,同時提高了最小二乘法計算策略梯度的靈活性,這也可以看作是Peters［2］所提出的eNAC方法的拓展變形.山地車仿真實驗結果表明,本文算法在性能上對最小二乘法的影響不大,但單步運算時間降低明顯,并且能夠根據具體的運算能力選擇合適的數據批量,從而使得該類方法適用于實際問題.

NAC-BRLS算法的收斂性沒有從理論上嚴格證明,特別是樂觀地更新策略導致策略非平穩.同時,計算自然梯度的運算復雜度隨狀態和動作空間的增大而迅速增加,把方法應用到更大狀態和動作空間下的效果有待嘗試.此外,每次進行迭代的數據量智能體可以根據實際的計算能力來自主選擇.

［1］SUTTON R S,BARTO A G.Introduction to reinforcement learning［M］.Cambridge：MIT,1998.

［2］PETERS J,SCHAAL S.Natural actor-critic［J］.Neurocomputing,2008,71（7）：1180- 1190.

［3］GRONDMAN I,BUSONIU L,LOPES G A D,et al.A survey of actor-critic reinforcement learning：standard and natural policy gradients［J］.IEEE Transactions on Systems,Man,and Cybernetics,Part C：Applications and Reviews,2012,42（6）：1291- 1307.

［4］程玉虎,馮渙婷,王雪松.基于參數探索的期望最大化策略搜索［J］.自動化學報,2012,38（1）：38- 45.

CHENG Yu-hu,FENG Huan-ting,WANG Xue-song.Expectation-maximization policy search with parameterbased exploration［J］.Acta Automatica Sinica,2012,38（1）：38- 45.

［5］BHATNAGAR S,SUTTON R S,GHAVAMZADEH M,et al.Natural actor：critic algorithms［J］.Automatica,2009,45（11）：2471- 2482.

［6］SUTTON R S.Learning to predict by the methods of temporal differences［J］.Machine Learning,1988, 3（1）：9- 44.

［7］ADAM S,BUSONIU L,BABUSKA R.Experience replay for real-time reinforcement learning control［J］.IEEE Transactions on Systems,Man,and Cybernetics, Part C：Applications and Reviews,2012,42（2）：201- 212.

［8］BRADTKE SJ,BARTO A G.Linear least-squares algorithms for temporal difference learning［J］.Machine Learning,1996,22（1／2／3）：33- 57.

［9］BOYAN J A.Technical update：least-squares temporal difference learning［J］.Machine Learning,2002,49（2／3）：233- 246.

［10］DANN C,NEUMANN G,PETERS J.Policy evaluation with temporal differences：a survey and comparison［J］.The Journal of Machine Learning Research, 2014,15（1）：809- 883.

［11］GEIST M,PIETQUIN O.Revisiting natural actor-critics with value function approximation［M］//Modeling Decisions for Artificial Intelligence.Berlin：Springer,2010：207- 218.

［12］CHENG Yu-hu,FENG Huan-ting,WANG Xue-song.Efficient data use in incremental actor：critic algorithms［J］.Neurocomputing,2013,116（10）：346- 354.

［13］XU Xin,HE Han-gen,HU De-wen.Efficient reinforcement learning using recursive least-squares methods［J］.Journal of Artificial Intelligence Research, 2002,16（1）：259- 292.

［14］AMARI S I.Natural gradient works efficiently in learning［J］.Neural computation,1998,10（2）：251- 276.

［15］BUSONIU L,ERNST D,SCHUTTER B D,et al.Online least-squares policy iteration for reinforcement learning control［C］//American Control Conference（ACC）.Baltimore：IEEE,2010：486- 491.

［16］郝釧釧,方舟,李平.采用經驗復用的高效強化學習控制方法［J］.華南理工大學學報：自然科學版,2012, 40（6）：70- 75.

HAO Chuan-chuan,FANG Zhou,LI Ping.Efficient reinforcement-learning control algorithm using experience reuse［J］.Journal of South China University of Technology：Natural Science Edition,2012,40（6）：70- 75.

［17］SUTTON R S,MCALLESTER D A,SINGH S P,et al.Policy gradient methods for reinforcement learning with function approximation［C］//Advances in Neural Information Processing Systems（NIPS）.Denver：MIT, 1999,99：1057- 1063.

［18］MOUSTAKIDES G V.Study of the transient phase of the forgetting factor RLS［J］.IEEE Transactions on Signal Processing,1997,45（10）：2468- 2476.

［19］LJUNG L,S¨ODERSTR¨OM T.Theory and practice of recursive identification［M］.Cambridge：MIT,1983.

［20］HACHIYA H,AKIYAMA T,SUGIAYMA M,et al.Adaptive importance sampling for value function approximation in off-policy reinforcement learning［J］.Neural Networks,2009,22（10）：1399- 1410.

［21］HUANG Zhen-hua,XU Xin,ZUO Lei.Reinforcement learning with automatic basis construction based on isometric feature mapping［J］.Information Sciences, 2014,286（1）：209- 227.

Natural Actor-Critic based on batch recursive least-squares

WANG Guo-fang,FANG Zhou,LI Ping
（School of Aeronautics and Astronautics,Zhejiang University,Hangzhou 310027,China）

The algorithm called natural actor-critic based on batch recursive least-squares（NAC-BRLS）was proposed in order to reduce the online computation burden of the agent and improve the real-time operation.The algorithm employed batch recursive least-squares in Critic to evaluate the natural gradient,and performed optimistic update in Actor by the estimated natural gradient.The use of batch recursive leastsquares enables the agent to adjust the date size of every batch according to its operational capability.A trade-off between fully optimistic and partially optimistic was made,improving the flexibility of NACLSTD.Simulation results in mountain car show that NAC-BRLS largely reduces the computational complexity without obviously affecting the convergence property compared with NAC-LSTD.

natural gradient；Actor-Critic；batch update；recursive least-squares

10.3785／j.issn.1008-973X.2015.07.019

TP 18

A

1008- 973X（2015）07- 1335- 08

2014- 12- 19. 浙江大學學報(工學版)網址：www.journals.zju.edu.cn／eng

國家自然科學基金資助項目（61004066）；浙江省自然科學基金資助項目（LY15F030005）.

王國芳（1989－）,男,博士生,從事強化學習、遷移學習的研究.ORCID：0000-0002-8331-5643.E-mail：gfwang89＠zju.edu.cn

方舟,男,副教授.ORCID：0000-0002-0733-958X.E-mail：zfang＠zju.edu.cn

下期論文摘要預登