考慮渦流反作用的永磁體渦流損耗解析計算

唐任遠　陳　萍　佟文明　韓雪巖

（沈陽工業大學國家稀土永磁電機工程技術研究中心　沈陽　110870）

考慮渦流反作用的永磁體渦流損耗解析計算

唐任遠陳萍佟文明韓雪巖

（沈陽工業大學國家稀土永磁電機工程技術研究中心沈陽110870）

推導了一種新型表面式無金屬護套永磁同步電機永磁體渦流損耗解析模型，該模型同時考慮渦流反作用、開槽引起的磁導諧波和渦流分布不均勻三種因素，可以計算任意定子電流波形的表面式無金屬護套永磁同步電機的永磁體渦流損耗，并能分析任意次數時空諧波產生的永磁體渦流損耗。采用所推導的解析模型研究影響永磁體渦流損耗的因素，包括調制比、載波比和氣隙長度。調制比和載波比的增加減小了電流時間諧波幅值二次方和，因此降低了永磁體渦流損耗；氣隙長度的增加，由于削弱了諧波電樞反應而降低了永磁體渦流損耗。通過對電機的實驗分析和有限元仿真，驗證了解析計算的正確性和規律的適用性。

無金屬護套的表面式永磁同步電機永磁體渦流損耗解析推導渦流反作用

0　引言

隨著電力電子技術的速猛發展和器件價格的不斷降低，變頻電源越來越多地應用于交流電動機調速系統中［1］。但變頻器的使用也引入了大量的電流時間諧波，影響永磁同步電機的損耗，而損耗是衡量電機效率的主要指標［2］。特別是永磁體渦流損耗，高頻使得感生的渦流密度增加，再加上轉子散熱條件有限，很容易導致永磁同步電機轉子溫升過高，引起永磁體的過熱退磁［3，4］。開關頻率為4kHz的變頻器，當諧波頻率達到5倍開關頻率時，對于釹鐵硼永磁電機，永磁體的透入深度為4.2mm（NdFeB材料的電導率為694 400S/m，相對磁導率為1.046），與中小型永磁電機的永磁體厚度相當，渦流反作用明顯，在計算永磁體渦流損耗時應考慮。

表面式永磁同步電機的轉子有兩種結構形式：一種是表面有一層金屬護套的結構，一般超高速的永磁電機較多使用此結構形式；另一種是永磁體表面使用無緯玻璃絲捆綁的結構。Z. Q. Zhu教授對帶金屬護套的永磁體渦流損耗進行了研究［5-7］，其提出的子域模型充分考慮定子開槽作用，但忽略了渦流反作用。文獻［8］雖考慮了渦流反作用，但忽略了開槽效應。對于無金屬護套的永磁電機，文獻［9，10］進行了永磁體渦流損耗的推導，但沒有考慮定子開槽和渦流反作用。文獻［11，12］提出了復雜磁導模型，但其模型基于復雜的保角變換關系，很難應用于損耗計算。文獻［13］通過引入實心轉子異步電機的端部系數來考慮永磁同步電機永磁體渦流損耗端部效應，但除了端部效應，還有很多因素導致渦流在永磁體上分布不均勻，致使2D方法計算永磁體渦流損耗不準確，而且該文并未進行實驗驗證，也沒有考慮開槽和渦流反作用。

目前主要有三種方法驗證永磁體渦流損耗：①通過損耗分離得到永磁體渦流損耗［14-16］；②通過自制實驗裝置測試永磁體渦流損耗［17，18］；③以溫升測試間接驗證永磁體渦流損耗［19，20］。

本文基于變頻器供電的實際，推導同時考慮渦流反作用、開槽效應和渦流分布不均勻效應的永磁體渦流損耗解析計算模型，該模型最大的優點是能夠計算任意定子電流波形和任意時空諧波產生的永磁體渦流損耗。基于該模型，對影響永磁體渦流損耗較大的因素（調制比、載波比和氣隙長度）進行分析，并通過實驗及有限元方法進行驗證。

1　解析解推導

在進行永磁體渦流損耗解析解推導的過程中，本文作了如下假設：

（1）定子開槽導致的磁導諧波對磁場的影響通過一個良好的磁導模型進行考慮。

（2）在對渦流反應場進行推導的過程中，認為永磁體只在軸向方向有渦流，而渦流分布不均勻對永磁體渦流損耗的影響將通過引入系數加以考慮。

（3）使用定子槽口等效電流片代替定子繞組。

（4）永磁體均勻且各向同性，其磁導率μm和電導率σm均為常數。

1.1物理模型

本文對無金屬護套結構的表面式永磁同步電機永磁體渦流損耗解析推導使用的模型如圖1所示。在極坐標系下，rr、rm和rs分別代表轉子外徑、永磁體外表面半徑和定子內徑；永磁體為rr～rm之間的 θ1～θ2的范圍；定子電流片均布在定子表面；轉子以ωr的角速度旋轉。

圖1　物理模型Fig.1　Physical model

1.2理論分析

1.2.1等效電流片的討論

參照文獻［21］，對等效電流片進行進一步推導。設三相繞組對稱，則三相電流為

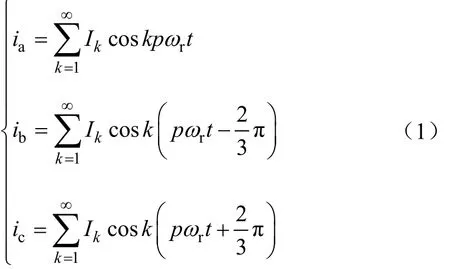
式中Ik——k次電流時間諧波的幅值；

p——電機極對數；

t——時間。

三相繞組電流片線電流密度的表達式為

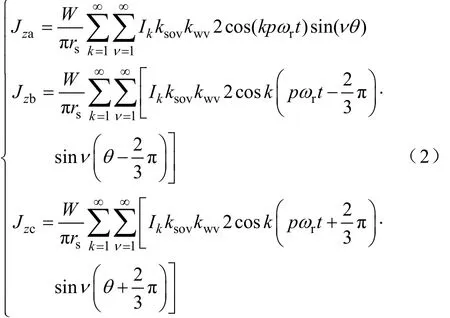
式中W——每相串聯匝數，W=Ns1Z1/（2ma）；

Ns1——每槽導體數；

Z1——電機定子槽數；

m——電機相數；

a——并聯支路數；

ν——磁場空間諧波次數；

ksov——槽口系數（具體計算參照文獻［1］）；

kwv——繞組系數（具體計算參照文獻［1］）；

θ——靜止坐標系下的周向角度。

令Jkν=3WIkksovkwv/（πrs），則三相合成電流片線電流密度表達式為

即

下文對式（4）進行討論。

（1）|k+ν|=3h，|k-ν|≠3h。滿足該條件的電流時間諧波k和磁場空間諧波次數ν 為：①當k=3h1+1時，ν=3h2+2；②當k=3h1+2時，ν=3h2+1。式中，h1=0，1，2，3，…；h2=0，±1，±2，±3，…。該類諧波的旋轉方向與基波旋轉方向相反。

（2）|k+ν|≠3h，|k-ν|=3h。滿足該條件的電流時間諧波次數k和磁場空間諧波次數ν 為：①當k=3h1+1時，ν=3h2+1；②當k=3h1+2時，ν=3h2+2。該類諧波的旋轉方向與基波旋轉方向相同。

（3）|k+ν |=3h，|k-ν|=3h。滿足該條件的電流時間諧波k和磁場空間諧波次數ν 為：①當k ≠ 3h1時，ν= 3h2；②當k= 3h1時，ν ≠ 3h2。該類諧波引起的電流片諧波合成分量為0，即這類諧波不會產生永磁體渦流損耗。

考慮到定子電流的初始相位φ，代表定子繞組的等效電流片線電流密度的式（3）和式（4）可簡化為［21］

式中Jkν——等效電流片線電流密度的k次電流時間諧波、ν 次磁場空間諧波幅值；

α——旋轉坐標系下的周向角度。

α=0代表A相繞組軸線位置，靜止坐標系和旋轉坐標系的關系為α=θ +ωrt。這樣，對于式（5）：當滿足條件（1）時，ν 取正值，Jkν=3WIkksovkwv/（πrs）；當滿足條件（2）時，ν 取負值，Jkν=-3WIkksovkwv/（πrs）；當滿足條件（3）時，Jkν=0。

1.2.2考慮渦流反應場的求解方程

1）氣隙中

極坐標系下，氣隙中的時變電磁場以矢量磁位AI（AI是rθ 平面上的量）的形式，由拉普拉斯方程表示

由于使用等效電流片，則式（6）的通解可寫成

式中，A、B為常數。

氣隙中磁通密度的徑向和切向分量分別為

2）永磁體中

由于存在渦流反應場，直接從永磁體出發來分析永磁體磁場并不準確。本文通過求解擴散方程，考慮趨膚深度，得出永磁體中的渦流密度JzⅡ（僅存在于z方向，這屬于電場的范疇）。通過Maxwell方程聯系電場和磁場，進而得出考慮渦流反作用的永磁體磁場。

式中δν——趨膚深度；

μ0——空氣磁導率，
μ0=4π×10-7H/m；
μm——永磁體磁導率；
σm——永磁體電導率。
式（10）的通解為

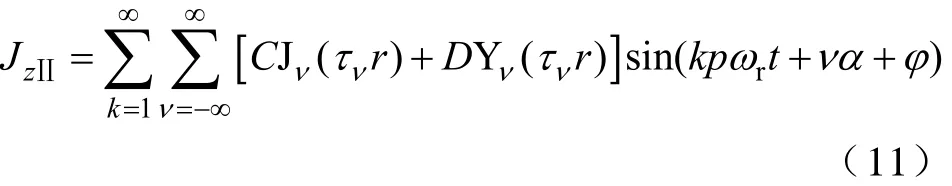
式中Jν（τνr）——ν次的一類Bessel函數；
Yν（τνr）——ν次的二類Bessel函數；

C，D——常數。

通過使用Maxwell等式聯系電場E和磁場B。

由式（12），將電場EⅡ用永磁體中的渦流密度JzⅡ表示，可得

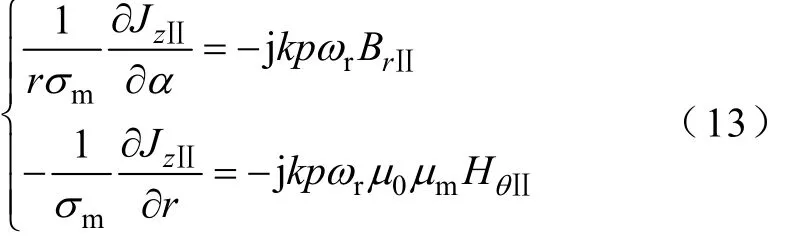
將式（11）代入式（13），則永磁體中的磁通密度徑向分量和磁場切向分量可表示為

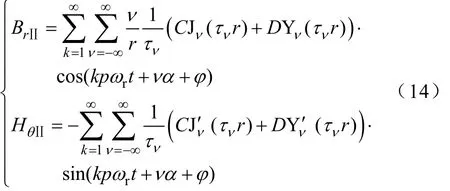
1.2.3邊界條件

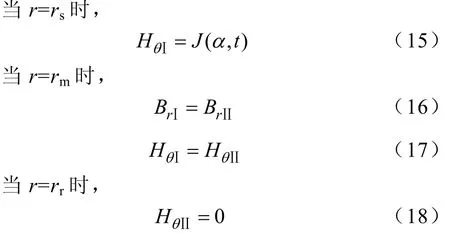
1.2.4場方程求解

將式（5）、式（9）和式（14）代入式（15）～式（18），得

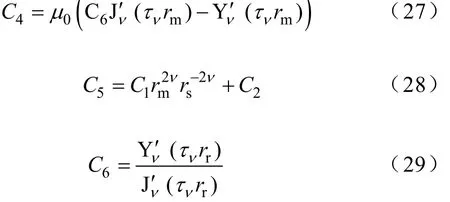
1.2.5考慮開槽對各場量進行修正

通過對文獻［22-24］的分析，整理出一個能綜合考慮各次磁導諧波的磁導模型，通過該磁導模型對各場量進行修正，得到更加準確的各場量數值。

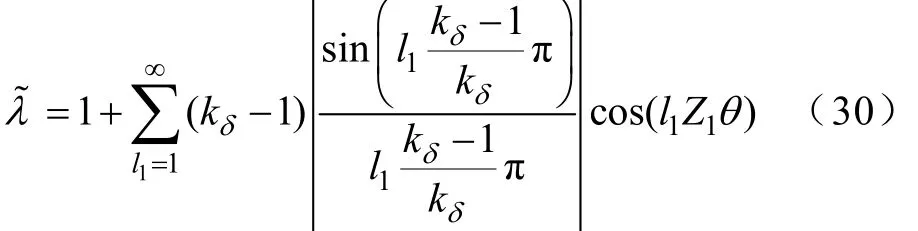
式中kδ——氣隙因數；

l1——磁導諧波次數。
對各場量進行修正［25］，得

1.2.6渦流分布不均勻的考慮

文獻［26］理論分析了2D和3D永磁體渦流損耗模型，得到3D情況下考慮渦流分布不均勻的永磁體渦流損耗系數F為

式中L——永磁體的長度；

W1——永磁體的寬度；

P3D——文獻［26］中3D永磁體渦流損耗解析解；

P2D——文獻［26］中2D永磁體渦流損耗解析解。

1.2.7永磁體渦流損耗的解析解

使用Poynting矢量方法計算永磁體內的渦流損耗。其表達式為

因此，在一個電周期T=2π/（pωr）內，平均每塊永磁體渦流損耗為

式中δ——氣隙長度。

2　各次時空諧波產生的永磁體渦流損耗

本文通過Matlab軟件編程對永磁體渦流損耗進行解析計算。

以一臺8極36槽，頻率為100Hz的6.5kW永磁同步電機為例，對各次諧波產生的永磁體渦流損耗進行分析。取一個周期電流進行諧波分析，如圖2所示。

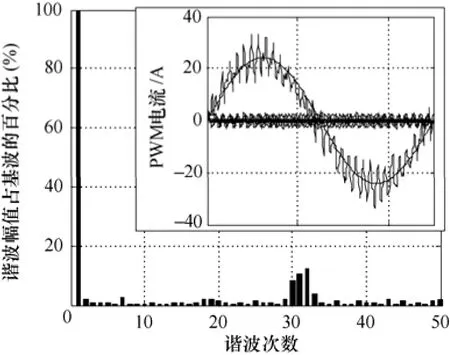
圖2　PWM電流波形的諧波分析Fig.2　Harmonic analysis of PWM current waveform

將分析得到的各次電流時間諧波幅值代入永磁體渦流損耗解析式中，以前13次電流時間諧波產生的前13次磁場空間諧波導致的永磁體渦流損耗為例，說明時空諧波產生的永磁體渦流損耗的規律，如圖3所示。

圖3　前13次時空諧波產生的永磁體渦流損耗Fig.3　Eddy current loss caused by time and spatial harmonics of fromt 13 times

圖3中時空諧波產生的永磁體渦流損耗較大的有：（1，2）（即基波電流時間諧波產生的2次磁場空間諧波，前面的數字代表電流時間諧波，后面的數字代表磁場空間諧波，下同）、（1，8）、（1，10）和（7，1）。1次電流時間諧波1次磁場空間諧波為基波，基波與轉子以相同的轉速旋轉，因此并不產生永磁體渦流損耗。且對于時空諧波次數滿足|k+ν|=0的諧波都與轉子同步速旋轉，均不感生永磁體渦流損耗。同時，當電流時間或磁場空間諧波次數為3的倍數時，這些諧波也不產生永磁體渦流損耗。

3　實驗

本文以該6.5kW永磁同步電機為例，對其進行附加諧波損耗實驗。實驗原理如圖4所示。實驗步驟如下：

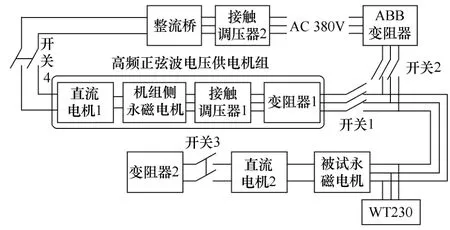
圖4　附加諧波損耗實驗原理Fig.4　Schematic diagram of additional harmonic losses test

（1）閉合開關2和開關3，進行溫升實驗。

（2）待被試電機溫升穩定之后，斷開開關3，斷開被試電機與直流電機2的連接，進行永磁電機的變頻器供電空載實驗。

（3）斷開開關2，閉合開關4和開關1，進行正弦波電壓供電空載實驗。

變頻器供電時，其電流時間諧波引起的損耗增量即為附加諧波損耗，又稱諧波損耗。IEC標準認為，空載與負載時附加諧波損耗的數值不變。本文通過變頻器供電空載實驗和正弦波電壓供電空載實驗即可得到附加諧波損耗，即

式中Pbht——附加諧波損耗的測試值；

P01PWM——變頻器供電空載輸入功率；

P01——正弦波電壓供電空載輸入功率；

PCuPWM——變頻器供電時銅耗；

PCu1——正弦波電壓供電時銅耗。

附加諧波損耗包括變頻器供電時的電流時間諧波在繞組、定轉子鐵心、周圍結構件和永磁體中產生的損耗。由于6.5kW額定頻率為200Hz，電流時間諧波在其繞組和周圍結構件中引起的附加諧波損耗非常小，本文忽略不計。因此，文中附加諧波損耗主要考慮電流時間諧波在定轉子鐵心和永磁體中的附加諧波損耗。

實際上，使用附加諧波損耗來驗證永磁體渦流損耗只驗證了電流時間諧波引起的永磁體渦流損耗（也稱附加諧波永磁體渦流損耗），而基波電流時間諧波產生的磁場空間諧波引起的永磁體渦流損耗是無法通過附加諧波損耗實驗來驗證的。

表1列出了6.5kW永磁同步電機附加諧波損耗實驗數據，通過表1可以得到6.5kW永磁同步電機的附加諧波損耗實測值為248.83W。

表1　附加諧波損耗實驗數據Tab.1　The test data of additional harmonic losses

表2給出了附加諧波損耗的解析計算值、FEM計算值和實驗值的對比。由于實驗條件的限制，無法對電流時間諧波引起的鐵耗和永磁體渦流損耗進行分離。因此，本文通過分別計算這兩項并求和的方法得到附加諧波損耗計算值，同時將附加諧波損耗計算值與實驗值加以對比。對于附加諧波永磁體渦流損耗的計算分別采用本文所推導的解析計算方法和3D有限元方法，而電流時間諧波引起的鐵耗則只用有限元計算方法。需要說明的是，對于鐵耗的有限元計算，為了考慮剪切加工的影響，本文對硅鋼片的損耗曲線進行了修正。但由于并未考慮沖壓等其他加工工藝對附加鐵耗的影響，加上實驗本身的誤差，使得計算值小于實驗值。

表2　附加諧波損耗計算值和實驗值的對比Tab.2　The comparison between calculation data and test data of additional harmonic losses

4　影響因素

從產生因素角度，永磁體渦流損耗可分為：①由于定子鐵心開槽導致的磁導諧波產生的永磁體渦流損耗；②定子繞組分布，基波電流導致的空間諧波磁場產生的永磁體渦流損耗；③定子電流時間諧波產生的永磁體渦流損耗。其中，定子電流時間諧波對永磁體渦流損耗的影響相當大。而調制比和載波比是影響電流時間諧波的重要因素。氣隙長度的改變通過電樞反應磁動勢的大小來影響永磁體渦流損耗，這種影響主要反映在磁場空間諧波引起的永磁體渦流損耗的變化上。這些因素的研究對永磁體渦流損耗的研究非常重要。

本文通過使用實測的電機輸入波形，使用本文的解析計算方法與有限元法分別進行計算，研究時間諧波產生的永磁體渦流損耗隨調制比和載波比的變化關系，并最終與實驗數據進行對比。

選取一臺6.9kW永磁同步電機做不同調制比與載波比下的附加諧波損耗實驗，實驗原理與圖4相似，但需要在ABB變頻器前加一個接觸調壓器。需要注意的是，該附加諧波損耗實驗并非是在溫升實驗的基礎上進行的，而是保持電機冷態，先做調制比實驗，再做載波比實驗。該電機的基波頻率為200Hz，8極36槽，氣隙長度為2mm。

假設鐵耗的FEM計算準確，則認為以下電流時間諧波引起的永磁體渦流損耗的實驗值是附加諧波損耗減去電流時間諧波引起的鐵耗的FEM計算值。

4.1調制比的影響

調制比為變頻器輸出線電壓基波幅值與直流母線電壓之比。保持開關頻率4kHz，即保持載波比為20，調節直流母線電壓，分別使調制比為0.55、0.60、0.65、0.70和0.75，記錄每個調制比下的輸入電流波形并進行諧波分析，計算前50次電流時間諧波產生的永磁體渦流損耗。不同調制比下電流時間諧波幅值的二次方和見表3。

表3　不同調制比時的電流時間諧波幅值二次方和Tab.3　Sum of squares of current time harmonics magnitudes in different modulation index

附加諧波永磁體渦流損耗隨不同調制比的電流時間諧波幅值二次方和的變化關系如圖5所示。可見，隨著調制比的增加，電流時間諧波幅值二次方和減小，電流時間諧波引起的永磁體渦流損耗也隨著減小，這就是調制比增加導致永磁體渦流損耗減小的原因。附加諧波永磁體渦流損耗的FEM和實驗結果趨勢基本相同，而解析方法得到的附加諧波永磁體渦流損耗隨電流時間諧波幅值二次方和基本呈線性關系，其擬合公式為

式中PPMbh——電流時間諧波引起的永磁體渦流損耗。

圖5　附加諧波永磁體渦流損耗隨不同調制比的電流時間諧波幅值二次方和的變化Fig.5　The variation of additional harmonics PM eddy current loss vs. sum of squares of current time harmonics magnitudes in different modulation index

4.2載波比的影響

載波比為供電變頻器載波頻率與電機基波頻率的比值。保持直流母線電壓598V，改變變頻器的開關頻率分別為1kHz、2kHz、3kHz、4kHz、8kHz和16kHz，即載波比分別為5、10、15、20、40和80，記錄每個載波比下的輸入電流波形并進行諧波分析，計算前50次電流時間諧波產生的永磁體渦流損耗。不同載波比下電流時間諧波幅值的二次方和見表4。附加諧波永磁體渦流損耗隨不同載波比的電流時間諧波幅值二次方和的變化關系如圖6所示。

可見，隨著載波比的增加，電流時間諧波幅值二次方和減小，電流時間諧波引起的永磁體渦流損耗也隨著減小，這就是載波比增加導致永磁體渦流損耗減小的原因。FEM計算結果和實驗結果趨勢基本相同。

解析方法計算得到的附加諧波永磁體渦流損耗呈兩種趨勢：在電流時間諧波幅值二次方和很小時，附加諧波永磁體渦流損耗的解析解比實驗值和FEM計算值小；在電流時間諧波幅值二次方和很大時，解析解則比實驗值和FEM計算值大。這是因為本文的解析方法計算永磁體渦流損耗是從定子側電流出發的，忽略了很多電機非線性關系的影響，因此，定子電流時間諧波對解析解的影響大一些。

從圖5和圖6可以看出，附加諧波永磁體渦流損耗和電流時間諧波幅值二次方和關系密切，由于改變調制比只是成比例地改變每次輸入電流時間諧波的幅值，因此，隨調制比的減小，電流時間諧波幅值二次方和呈線性增加，由式（36）可知，電流時間諧波引起的永磁體渦流損耗也線性增加。

而隨載波比的減小，各次電流時間諧波幅值并非呈比例增加，其值有大有小，因此，電流時間諧波幅值二次方和與附加諧波永磁體渦流損耗并非線性關系。

在永磁體渦流損耗的抑制技術中，增加調制比和載波比固然能降低永磁體渦流損耗，但這需要在特定的環境下才可行。而且增加載波比會嚴重增加變頻器的功率損耗，而調制比的調節范圍也是有限的。因此，應根據電機工作的實際情況合理選擇調制比和載波比。

表4　不同載波比時的電流時間諧波幅值二次方和Tab.4　Sum of squares of current time harmonics magnitudes in different frequency-carrier ratio

圖6　附加諧波永磁體渦流損耗隨不同載波比時的電流時間諧波幅值二次方和的變化Fig.6　The variation of additional harmonics PM eddy current loss vs. sum of squares of current time harmonics magnitudes in different frequency-carrier ratio

4.3氣隙長度的影響

改變氣隙長度，永磁體磁化方向長度也隨之變化，氣隙越長，永磁體磁化方向長度越大，永磁體用量越多。本文以一臺2.1kW永磁同步電機為例，進行解析計算和有限元分析。該電機的有限元三維剖分圖如圖7所示。該電機8極36槽，額定頻率為266.7Hz，額定轉速為4 000r/min。采用ABB通用變頻器供電，其開關頻率為4kHz。

圖7　2.1kW永磁同步電機剖分圖Fig.7　Grid map of 2.1kW PMSM

本文對1.0mm、1.25mm、1.5mm、1.75mm和2.0mm五種氣隙長度下的永磁體渦流損耗進行解析計算和有限元分析。保證該2.1kW永磁同步電機的空載反電動勢大小基本不變，得到的永磁體渦流損耗隨氣隙長度的變化關系如圖8所示。由圖8可見，解析計算和FEM計算結果趨勢相同，其數值稍有偏差。則根據FEM計算結果可知永磁體渦流損耗PPM隨氣隙長度的變化關系擬合式為

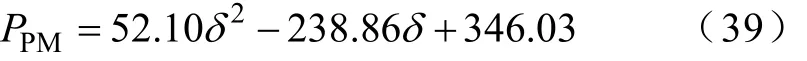
圖8　永磁體渦流損耗隨氣隙長度的變化趨勢Fig.8　The variation trend of PM eddy current loss vs. different air gap lengths

由式（39）可知，改變氣隙長度，不僅改變了基波產生的磁場空間諧波所引起的永磁體渦流損耗，同時也改變了電流時間諧波產生的磁場空間諧波所導致的永磁體渦流損耗。而氣隙長度變大導致的永磁體渦流損耗減小主要是由于基波電流時間諧波產生的磁場空間諧波的變化。

如圖9所示，不改變電機的輸入電流，則基波和各次電流時間諧波的幅值不發生改變。對不同氣隙長度下前25次磁場空間諧波所引起的永磁體渦流損耗進行分析，可以看出，隨著氣隙長度的增大，永磁體渦流損耗總體變小，但增加了永磁體的用量。氣隙長度的增加，對基波磁場空間諧波與2次磁場空間諧波以及每個3h3+1和3h3-1次磁場空間諧波導致的永磁體渦流損耗都有所減小（h3=1，2，3，…），但是減小的幅度不同，基波磁場空間諧波與2次、8次磁場空間諧波產生的永磁體渦流損耗減小的幅度較大。

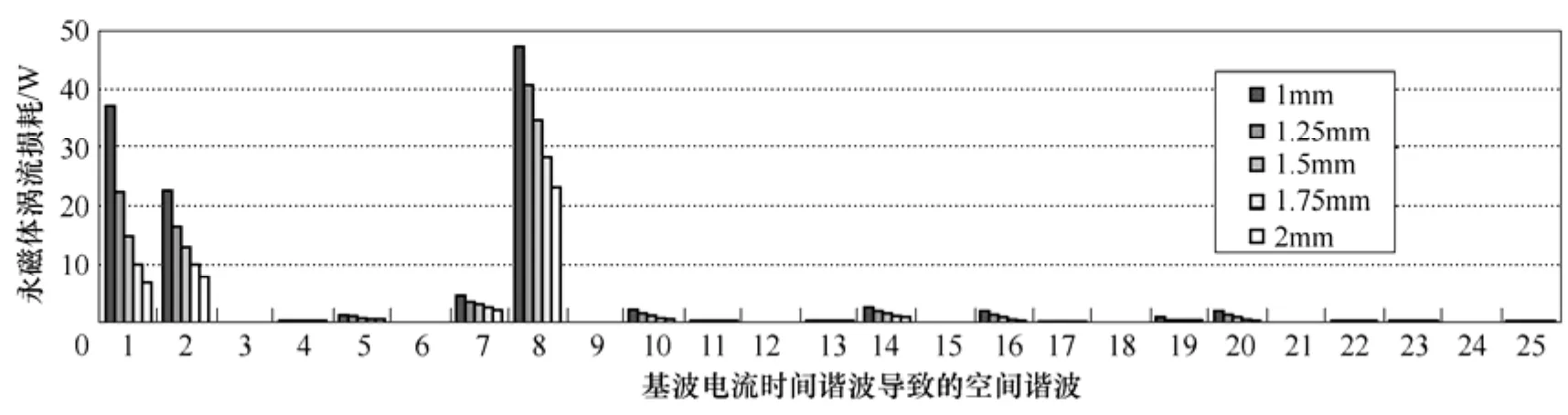
圖9　不同氣隙長度對基波電流時間諧波導致的磁場空間諧波產生的永磁體渦流損耗的影響Fig.9　The influence of different air gap lengths vs. eddy current loss due to magnetic spatial harmonics caused by fundamental current time harmonic

5　結論

本文從理論上推導出一種新型表面式無金屬護套型永磁同步電機永磁體渦流損耗解析模型，該模型考慮渦流反應場、開槽導致的磁導諧波和永磁體上感生渦流的分布不均勻效應，其最大優點在于能夠對各次時空諧波產生的永磁體渦流損耗進行解析計算。對影響永磁體渦流損耗的因素進行了分析：

（1）對嚴重影響電流時間諧波的調制比和載波比進行了分析，得出永磁體渦流損耗隨調制比和載波比增加而減小的主要原因是電流時間諧波幅值二次方和的減小。其中，調制比的增加導致電流時間諧波幅值二次方和的減小，其所引起的永磁體渦流損耗的減小是成比例的，本文的解析推導驗證了這一關系。

（2）增加氣隙長度，主要減小了基波電流時間諧波產生的永磁體渦流損耗。且對基波電流時間諧波產生的各次磁場空間諧波引起的永磁體渦流損耗都有所減小，特別是1次、2次和8次空間諧波。通過實驗與有限元方法的驗證了本文解析計算方法的精確性和規律的適用性。

［1］ 唐任遠. 現代永磁電機理論與設計［M］. 北京： 機械工業出版社，2006.

［2］ 方程，許海平，薛劭申，等. 直驅型多相永磁同步電機轉矩脈動及損耗特性［J］. 電工技術學報，2014，29（5）： 150-159.

Fang Cheng，Xu Haiping，Xue Shaoshen，et al. Torque ripple and losses of direct-drive multi-phase permanent magnet synchronous machines［J］. Transactions of China Electrotechnical Society，2014，29（5）：150-159.

［3］ 韓守亮，崔淑梅，王鐵成，等. 分數槽集中繞組永磁電機在模塊化級聯電機系統上的應用［J］. 電工技術學報，2013，28（3）： 9-15.

Han Shouliang，Cui Shumei，Wang Tiecheng，et al. Application of fractional-slot concentrated winding permanent magnet machines in modular cascade machine system［J］. Transactions of China Electrotechnical Society，2013，28（3）： 9-15.

［4］ 孔曉光，王鳳翔，邢軍強. 高速永磁電機的損耗計算與溫度場分析［J］. 電工技術學報，2012，27（9）：166-172.

Kong Xiaoguang，Wang Fengxiang，Xing Junqiang. Losses calculation and temperature field analysis of high speed permanent magnet machines［J］. Transactions of China Electrotechnical Society，2012，27（9）：166-172.

［5］ Wu L J，Zhu Z Q，Staton D，et al. An improved subdomain model for predicting magnetic field of surface-mounted permanent magnet machines accounting for tooth-tips［J］. IEEE Transactions on Magnetics，2011，47（6）： 1693-1704.

［6］ Zhu Z Q，Wu L J，Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines［J］. IEEE Transactions on Magnetics，2010，46（4）： 1100-1115.

［7］ Wu L J，Zhu Z Q，Staton D，et al. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines［J］. IEEE Transactions on Magnetics，2012，48（3）： 1234-1247.

［8］ Zhu Z Q，Ng K，Schofield N，et al. Improvedanalytical modeling of rotor eddy current loss in brushless machines equipped with surface-mounted permanent magnets［C］. IEE Proceedings on Electric Power Applications，2004，151（6）： 641-650.

［9］ 張磊，高春俠. 永磁同步電機磁鋼渦流損耗模型及其衡量指標［J］. 電機與控制學報，2013，17（7）： 46-53.

Zhang Lei，Gao Chunxia. Eddy-current loss model and index for magnets of permanent magnet synchronous motors［J］. Electric Machines and Control，2013，17（7）： 46-53.

［10］ Bellera A，Bali H，Belfkira R，et al. Analytical prediction of open-circuit eddy-current loss in series double excitation synchronous machines［J］. IEEE Transactions on Magnetics，2011，47（9）： 2261-2268.

［11］ 江善林. 高速永磁同步電機的損耗分析與溫度場計算［D］. 哈爾濱： 哈爾濱工業大學，2010.

［12］ Zarko D，Ban D，Lipo T A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance［J］. IEEE Transactions on Magnetics，2006，42（7）： 1828-1837.

［13］ Boughrara K，Ibtiouen R，Touhami O，et al. Analytical and numerical calculation of magnetic field distribution in the slotted air-gap of tangential surface permanent-magnet motors［J］. Serbian Journal Electrical Engineering，2009，6（1）： 15-31.

［14］ 徐永向，胡建輝，胡任之，等. 永磁同步電機轉子渦流損耗計算的實驗驗證方法［J］. 電工技術學報，2007，22（7）： 150-154.

Xu Yongxiang，Hu Jianhui，Hu Renzhi，et al. An experimental verification method of calculation for rotor eddy current losses in PMSMs［J］. Transactions of China Electrotechnical Society，2007，22（7）： 150-154.

［15］ 徐永向，胡建輝，鄒繼斌. 表貼式永磁同步電機轉子渦流損耗解析計算［J］. 電機與控制學報，2009，13（1）： 63-66，72.

Xu Yongxiang，Hu Jianhui，Zou Jibin. Analytical calculation of rotor eddy current losses of surfacemounted PMSM［J］. Electric Machines and Control，2009，13（1）： 63-66，72.

［16］ 邢軍強. 高速永磁電機轉子損耗及通風散熱研究［D］. 沈陽： 沈陽工業大學，2011.

［17］ 沈啟平. 車用高功率密度永磁同步電機的研究［D］.沈陽： 沈陽工業大學，2012.

［18］ Aoyama Y，Miyata K，Ohashi K. Simulations and experiments on eddy current in Nd-Fe-B magnet［J］. IEEE Transactions on Magnetics，2005，41（10）： 3790-3792.

［19］ 解恩，劉衛國，羅玲，等. PWM調制對無刷直流電機轉子渦流損耗的影響［J］. 電工技術學報，2013，28（2）： 117-125.

Xie En，Liu Weiguo，Luo Ling，et al. Influence of PWM on rotor eddy-current losses in brushless DC motor［J］. Transactions of China Electrotechnical Society，2013，28（2）： 117-125.

［20］ Zhao N，Zhu Z Q，Liu W. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator［J］. IEEE Transactions on Magnetics，2011，47（10）： 4199-4202.

［21］ Zhu Z Q，Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors，Part II： Armature-reaction field［J］. IEEE Transactions on Magnetics，1993，29（1）： 136-142.

［22］ Zhu Z Q，Howe D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors，Part III： Effect of stator slotting［J］. IEEE Transactions on Magnetics，1993，29（1）： 143-151.

［23］ 宋志環. 永磁同步電動機電磁振動噪聲源識別技術的研究［D］. 沈陽： 沈陽工業大學，2010.

［24］ Huang S，Aydin M，Lipo T A. Electromagnetic vibration and noise assessment for surface mounted PM machines［C］. IEEE Power Engineering Society Summer Meeting，2001： 1417-1426.

［25］ Zhu Z Q，Howe D. Instantaneous magnetic field distribution in permanent magnet brushless DC motors，Part IV： Magnetic field on load［J］. IEEE Transactions on Magnetics，1993，29（1）： 152-158.

［26］ Ruoho S，Santa-Nokki T，Kolehmainen J，et al. Modeling magnet length in 2-D finite-element analysis of electric machines［J］. IEEE Transactions on Magnetics，2009，45（8）： 3114-3120.

Analytical Calculation of Eddy Current Loss Accounting for Eddy Current Reaction

Tang RenyuanChen PingTong WenmingHan Xueyan

（National Engineering Research Center for Rare Earth Permanent Magnet Machines
Shenyang University of TechnologyShenyang110870China）

This paper deduces a novel analytical model of permanent magnet （PM） eddy current loss for surface mounted permanent magnet synchronous motor （PMSM） without metal shell，accounting for eddy current reaction，permeance harmonics due to slot and the unevenness of eddy current. This model can calculate eddy current loss with any stator current waveform in surface mounted PMSM without metal shell and can analyze PM eddy current loss caused by any time and spatial harmonics. By using this analytical model，the factors that affect PM eddy current loss are studied，including modulation index，frequency-carrier ratio and air gap length. With increasing the modulation index and frequency-carrier ratio，the sum of squared current time harmonics magnitudes decreases，and accordingly the PM eddy current loss decreases. The increase of air gap length wakens the harmonics armature reaction which decreases the PM eddy current loss. The calculated results and analysis are verified by tests and finite element method （FEM）.

Surface mounted permanent magnet synchronous motor without metal shell，permanent magnet eddy current loss，analytical derivation，eddy current reaction

TM351

唐任遠男，1931年生，教授，中國工程院院士，研究方向為稀土永磁電機與計算電磁學。

陳萍女，1987年生，博士研究生，研究方向為稀土永磁電機損耗與溫升計算。（通信作者）

國家科技支撐計劃（2013BAE08B00），國家自然科學基金（51307111）和遼寧省教育廳科學技術研究項目（L2013049）資助。

2014-10-08改稿日期 2014-12-23