基于遺傳算法的煙草輸送機振槽排樣優化算法

張世龍，趙罘，薛美榮，李娜

（北京工商大學材料與機械工程學院，北京　100048）

基于遺傳算法的煙草輸送機振槽排樣優化算法

張世龍，趙罘，薛美榮，李娜

（北京工商大學材料與機械工程學院，北京100048）

針對煙草輸送機振槽加工材料浪費率高的問題，提出了遺傳算法對其進行優化排樣。確定了適用于排樣優化的編碼方式，編寫了選擇算子，交叉算子及變異算子，在Matlab上編寫程序并得到實現。實例測試結果表明通過遺傳算法對其進行優化排樣可有效提升材料利用率。

振槽；遺傳算法；排樣優化

0　引言

在煙草生產過程中，煙草輸送一般都是通過輸送機帶動振槽進行往復振動，從而使得煙草在振槽中進行前進運動。由于需要長期進行往復振動，所以振槽比較容易損壞。為了保證穩定生產，需要定期更換振槽。由于煙草輸送線比較長，所以振槽也相應比較長，在生產振槽過程中，往往是用多條小矩形母材加以焊接拼接而成。

然而目前多數企業在實際生產中仍是根據目測和經驗，采用手工進行排樣。排樣工人預先用一些材料做出零件模型，當需要在板料上加工某些零件時，把這些零件的模型盡可能緊密地放在板料上，沿模型的輪廓把形狀畫出來，然后再進行切割。排樣工人通過反復排放、比較來尋求較好的排放方案，勞動強度高、工作量大且效率和材料利用率都較低。故本文旨在基于遺傳算法提出一個有效的求解輸送機振槽排樣問題的方法，以期提高材料的利用率。

1　遺傳算法

1975年，J.H.Holland教授受生物學中“生物進化”和“自然選擇”學說的啟發，提出了著名的遺傳算法。遺傳算法可看成一種全局數值優化，它模擬基因重組與進化的自然過程，把待解問題的參數編成二進制碼，稱為“基因”，若干基因組成一個“染色體”。許多染色體進行類似于自然選擇、雜交和變異的運算，經過多次重復運算（即世代遺傳），直至得到最后的優化結果［1］。圖1是遺傳算法的基本流程圖。

1.1數學模型

設振槽展開后矩形的長為L，寬為W。有K種矩形母材，其中長、寬分別為li、wi，即可橫放也可豎放，如圖2所示。

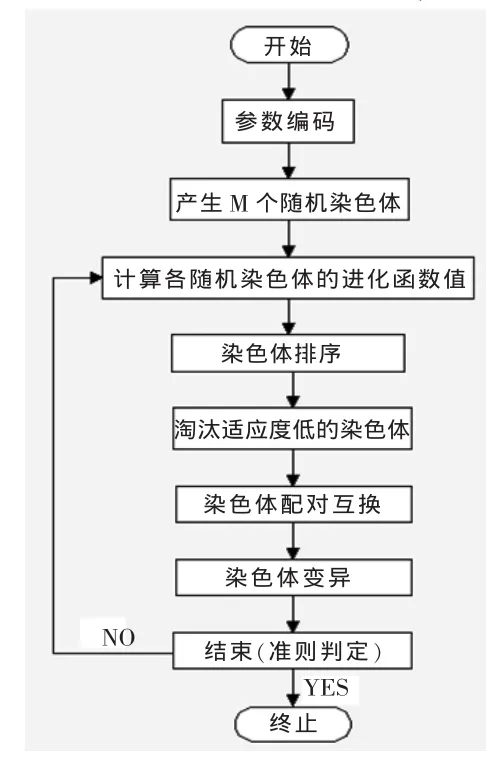
圖1　遺傳算法的基本流程圖Fig.1 Basic flow figure of genetic algorithm

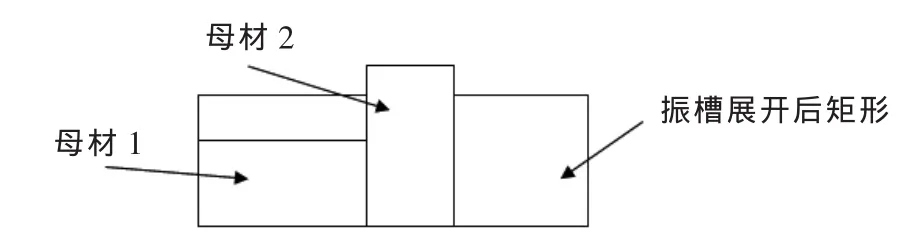
圖2　數學模型圖Fig.2 Figure of mathematical model

為了使得只在一個方向上有焊縫，需要所使用母材在寬度方向比目標振槽寬度寬，然后一條一條通過焊接得到最終振槽矩形。因此在縱向方向只能排放一行母材，一行上的母材只能被橫放或豎放，假設板材的數量總是足夠的。我們用yi表示橫放時的零件個數，xi表示豎放時的零件個數。目標函數：

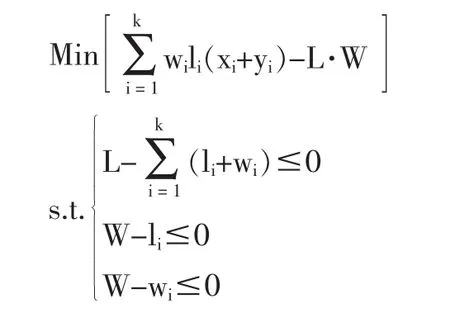
這是一個多維有約束離散優化問題。其已知參數為W、L、wi、li，未知參數為xi、yi。用傳統優化方法很難找到有效的算法對其求解。根據遺傳算法的特點，我們對這一問題考慮了遺傳算法的可行性。為了使問題簡單化，將一個矩形件（li，wi）看成（li，wi）和（wi，li）兩種不同的矩形件考慮。這樣，上面的數學模型變為以下形式。目標函數：

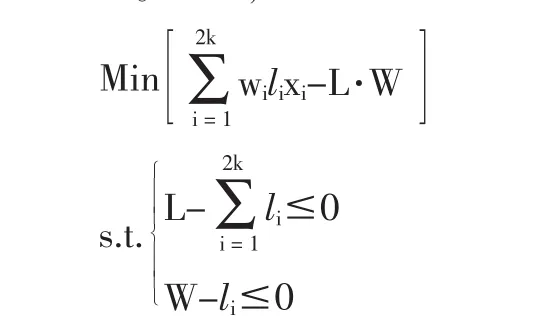
1.2遺傳算法模型

（1）編碼。染色體編碼是指將矩形件排樣問題的可行解從其解空間轉換到遺傳算法能夠處理的搜索空間的解。在遺傳算法中，用染色體表示問題的一個可能解，其編碼方式通常有二進制編碼、實數編碼和符號編碼等［2］。基于問題特點，此處采用十進制編碼方式：每個矩形件的編號作為染色體（問題解）的一個基因，所有矩形件編號所構成的序列代表各矩形件的排樣順序，這樣的一個序列就是一個染色體。

（2）選擇算子。選擇算子是為了避免有效基因的損失，使高性能的個體得以更大的概率生存，從而提高全局收斂性和計算效率。選擇算子采用輪盤賭選擇法［3］，具體過程為：①對種群中每個個體預排樣，求出每個個體的適應度值，再求出所有個體的適應度值總和；②求出每個個體的相對適應度，也就是被選中概率，pi=Fi/Fsum。其中pi表示第i個個體被選中概率；Fi表示第i個個體的適應度值；Fsum表示所有個體的適應度值之和；③求出每個個體的的累積選擇概率；④產生一個隨機數rand=［0，1］。若rand＜qi，第一個個體被選中，否則第i個個體被選中，使qi-1＜rand＜qi成立。重復該操作，直到選擇的個體數等于初始種群的個體總數。

（3）交叉算子。交叉算子在遺傳算法中起著關鍵的作用，通過交叉可產生新的個體。常用的交叉算子有單點交叉、兩點交叉、多點交叉等［4］。

設定交叉操作算子的方法如下：在染色體上選擇一個位置作為交叉位置，交叉位置之前的基因片段不交叉，交叉位置之后的片段交叉。比較兩個參與交叉的染色體，將交叉位置之前的相同基因去除，將交叉位置之前的剩余基因順序不變的存入數組p［］和q［］中。然后對染色體的交叉部分進行交叉，若交叉部分的基因不等于這兩個數組中基因，則直接交換；若與數組中的基因相同，則先把相同基因換成數組p［］或q［］中對應基因之后再交換。

（4）變異算子。變異算子是將染色體中的某些基因位上的基因值加以改變，從而產生一個新的個體。變異算子一方面可以使遺傳算法具有局部的隨機搜索能力，另一方面有助于遺傳算法維持群體的多樣性，防止出現早熟現象［5］。

（5）停止準則。遺傳算法收斂判斷準則較多，比較常見的是根據迭代次數以及解的質量來判斷。迭代次數是表示遺傳算法運行終止條件的一個主要參數，它表示遺傳算法運行到規定的進化代數之后就停止運行，并將當前群體中的最佳個體作為所求問題的最優解輸出。

2　振槽排樣優化實例及分析

本文通過上述的遺傳算法編制了計算程序，并在Matlab上進行了實現。在實驗中取群體規模N=40，交叉概率Pr=0.7，變異概率Pm=0.05或0.15。企業現用的母材數據如表1所示。

表1　矩形件信息Tab.1 Rectangular parts information

共有4種母材，每種母材的數量都是一定的，現在要加工一個輸送機振槽，振槽展開后矩形的長為16000mm，寬為1200mm。為了得到這個振槽，在Matlab上通過500代的迭代計算，當變異概率為0.05時，得到排樣的材料利用率為96.69%，當變異概率為0.15時，得到排樣的材料利用率為97.65%。

可見本文提出的排樣算法在提高板材利用率方面有一定的優越性。

3　結論

本文用遺傳算法來求解煙草輸送機振槽的排樣問題，可有效解決振槽在加工生產中浪費材料和費時、費工的問題。

到目前為止，對優化排樣問題的研究，無論是一維、二維還是三維，帶約束或不帶約束，都沒有出現針對這一問題的系統化解決方案。由于問題的多樣性，大多數研究都只是停留在對某些算法的部分改進，以適應各自的問題，假如能夠建立一套完整的排樣理論體系，必將大大推進排樣問題的研究，減少重復性工作。

［1］曹炬，周濟.矩形件排樣優化的一種近似算法［J］.計算機輔助設計與圖形學學報，2009，3.

［2］劉德全，滕弘飛.矩形件排樣問題的遺傳算法求解［J］.小型微型計算機系統，1998，12.

［3］趙新芳，崔耀東，徐瑩.矩形件帶排樣的一種遺傳算法［J］.計算機輔助設計與圖形學學報，2008，4.

［4］減輝.遺傳算法及其應用［J］.武漢科技學院學報，2005，4.

［5］葉軍君，殷國富.板材下料優化排樣CAD系統的研究［J］.現代制造工程，2004，10.

Optimization Algorithm for Vibration Slot of Tobacco Vibrating Conveyor Based on Genetic Algorithm

ZHANG Shi-Long，ZHAO Fu，XUE Mei-Rong，LI Na
（School of Materias and Mechanical Engineering，Beijing Technology and Business University，Beijing 100048，China）

Aiming at the problem of high wastage rate of vibration slot processing material in tobacco conveyer，the genetic algorithm was proposed to optimize the layout.Encoder mode of layout optimization was determined.The selection operator，crossover operator and mutation operator were designed，and the program was written in Matlab.The test results of the examples show that the method can effectively improve the utilization of materials by the genetic algorithm.

vibration slot；genetic algorithm；layout optimization

TH122

A

10.3969/j.issn.1002-6673.2015.06.014

1002-6673（2015）06-040-03

2015-09-10

項目來源：北京工商大學研究生科研能力提升計劃項目資助（2015）

張世龍（1991-），男，河南信陽人，研究生。主要研究方向：機械設計及理論；通訊作者：趙罘（1972-），男，吉林長春人，副教授。