幾何直觀讓學生的思維從晦澀走向簡約

鄭文慶

幾何直觀是利用動作、圖形洞察數學本質的一種方式，既有形象思維的特征，又有抽象思維的特點。它可以通俗、生動地揭示數學的本質，把復雜的數學問題變得簡明、形象，有利于學生探索解決問題的思路，預測結果，促進數學理解，提高思維轉化能力。那么，如何借助幾何直觀，讓學生的思維從晦澀走向簡約呢？

一、借助動手操作，讓思維從抽象走向直觀

動手操作是一種以“動”促“思”，調動學生全身心投入學習過程的有效形式。因而，在課堂上，要盡量給學生提供動手操作的機會。當然，操作活動的目的是為了使學習內容直觀化，讓每一位學生都有機會參與，為他們積累豐富的感性認識。當然，在操作活動中，不能為操作而操作，而應有意識地引導學生自覺地思考、探索，學會用自己的語言說明操作的過程以及得到一些結論。

如，單元試卷中有這樣一道填空題：“把一條繩子對折再對折，然后從中間剪開，一共可以剪成（ ）段。”學生的答案可謂五花八門，但大體上有三種：3段、4段和5段。

其實，只要教師留意，就能發現：這種題不僅在低中年級出現，也常在高年級出現，甚至在奧數競賽中也經常出現，只不過是對折的次數不同罷了。

既然這種題型出現的頻率較高，而學生答題的正確率又很低，何不作為實踐活動的第一手素材，引導學生探究一下這個問題呢？

于是，教師事先布置學生準備好剪刀、羊毛線（代替繩子）等工具和材料，上一節數學實踐活動課——“剪繩子問題”。教師先讓學生剪一剪，積累一定的感性認識。接下來再讓學生填一填，完成下面這個表格，并帶著問題思考：剪成的總段數與對折的次數的關系如何？

總段數與對折次數關系統計表

學生填完表后，剪成的總段數與對折的次數的關系已經漸漸明朗、清晰起來，初步形成規律：一根繩子對折一次后，從中間剪開，會剪成3段（兩端加一，即2+1）;一根繩子對折兩次后，從中間剪開，會剪成5段（2×2+1）;如果繼續對折，從中間剪開，對折幾次，就會得到幾個2相乘再加1的段數。

看似枯燥的一道思考題，因賦予其操作的成份，“化靜為動”，把靜態的知識轉化為動態呈現，動靜結合，就能讓學生在具體、直觀的操作活動中理解數量關系，問題的解決也就變得觸手可及乃至水到渠成。

二、依托畫圖方法，讓思維從障礙走向疏通

畫圖也是一種重要的幾何直觀方法。教學中，教師可以引導學生借助圖形分析題意，包括分析已知條件和問題，并逐步上升到能將直觀圖與數學語言、符號語言進行合理轉換，從而解決實際問題。

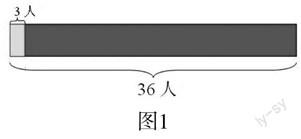
如，“36人植樹，每組3人，可以分成多少組？”這道題從除法的意義來說是包含除法。學生從二年級第一次認識除法到三年級的繼續學習，包含除法一直是難點。為此，教學時，教師采用了畫圖的方法，并結合圖形理解問題（如圖1）：

圖1

36人植樹，每組3人，能分成多少組，就是要求36里面包含了多少個3？

這樣的直觀演示符合學生的思維發展規律，也降低了難度，便于學生領會、掌握。

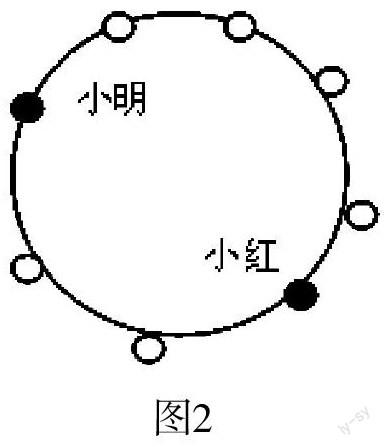
畫圖的方法不僅能幫助學生理解問題，也能幫助他們理解數量關系。如，有一道這樣的題目：“下課時，小朋友們圍成一圈做游戲，從小明開始向左數，小紅是第6個人，從小紅開始往左數，小明是第4個人，一共有幾個人？”很多一年級學生感到很難，或者能夠想出結果卻不會列算式，教師不妨引導他們用畫圖的方法幫助理解數量關系。（如圖2）

圖2

通過畫圖，將復雜的問題變得簡單，這樣學生就很容易列出算式：6+4-2=8（人），也理解了“-2”是因為在計算總人數時，小明、小紅分別多算了一次。

三、凸顯形數結合，讓思維從模糊走向清晰

數形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來。通過“以形助數”或“以數解形”，可以使復雜問題簡單化，抽象問題具體化，從而讓思維從模糊走向清晰。

如，看圖了想一想，可以把這個算式轉化成怎樣的算式計算。

圖3

教學時，教師可以分三個層次進行教學，在解決問題的過程中培養學生的幾何直觀能力。第一層次：指導看圖，學會轉化。呈現算式后，教師可以給學生一些思考的時間和空間，學生一般會應用通分的方法，轉化成同分母分數進行計算。這時，教師可以鼓勵學生思考其他的方法。當學生思維受阻時，才出示直觀圖，先結合各個分數理解直觀圖中各部分的意義，再啟發學生將其轉化為1-進行計算。第二層次：適當拓展，突出直觀。教師將算式拓展到1++++…+，要求學生選擇上面的方法進行計算，學生一般會根據畫直觀圖的方法，將算式轉化為1-進行計算。這時，教師要引導學生思考：為什么要用畫直觀圖的方法？使學生體會數與形的完美結合，從而將復雜的算式轉化成簡單的算式進行計算。第三層次：深度思考，強化直觀。教師可以啟發學生觀察分母的特點：分母分別是2、2個2相乘、3個2相乘、4個2相乘……在直觀圖上對應的是先把正方形平均分成2份，取其中的1份;再把剩下的圖形平均分成2份，取其中的1份……最后分出的圖形與剩下的圖形相等。借助直觀圖，要求涂色部分的大小，只要用單位“1”減去剩下圖形的大小。從而，把復雜的計算問題轉化成簡單的計算問題的同時，又初步培養了學生的幾何直觀意識。

四、注重遷移類推，讓思維從膚淺走向深刻

小學數學教材的編寫有兩條線索：一是處于表面的知識;二是隱含于知識背后的模型思想。教師只有創造性地使用教材，變“教教材”為“用教材”，做到源于教材而高于教材，才能領會知識深處的數學基本思想。

如，人教版數學一年級下冊第73頁的一道思考題：跳繩比賽中，小紅和參加比賽的每個人握一次手，一共握了39次。參加跳繩比賽的一共有多少人？教學時，教師可以先通過握手、觀察、思考等一系列數學活動，為學生提供充裕的實踐活動的時間和空間。接著，讓學生選擇自己喜愛的圖形，分別表示握手的人數和參賽的人數，自主探索圖形中隱藏的秘密：參賽人數比握手人數多1（握手人數比參賽人數少1）。再讓學生舉例子，根據思考題的數量關系進行“異”題“同”構：每道題目的數量關系相似，通過類比訓練，一方面有助于培養學生的聯想思維能力，另一方面有助于分析、比較異同，抓住數學本質。最后，借助當堂訓練，既溝通了本冊教材第12頁“我們一共有10個男生，老師讓相鄰兩個男生之間站一個女生。一共可以站進多少個女生？”與這道思考題數量關系的聯系，又溝通了小學數學中常見的植樹問題、上樓問題、鬧鐘問題，乃至鋸木頭問題、電線桿問題、插彩旗問題與這道思考題的聯系，發現了“間隔數與點數之間的關系”的規律，實現了有效建構。

教學諸如此類的思考題時，教師千萬不能走過場、就題論題，而應當有意識地抓住典型材料，把各個知識點連成線、形成面、結成體。解題過程中，部分學生也許不甚理解，但大部分學生親身經歷、體驗、感悟模型的建構過程，基本上會用自己的語言來表述，在頭腦中留下久遠而深刻的記憶。到了高年級，碰到類似的問題，他們沉睡的思維記憶就會重新被激活，解題的關鍵就會被抓住，數感也得到培養。

◇責任編輯：徐新亮◇